Amidoxime Polymers for Uranium Adsorption: Influence of Comonomers and Temperature
Abstract
:1. Introduction
1.1. Background
1.2. Review of Materials Tested for Uranium Adsorption
1.2.1. Non–Amidoxime Materials
1.2.2. Japanese Amidoxime Adsorbents
1.2.3. ORNL Amidoxime Adsorbents
1.3. Focus of This Study
2. Materials and Methods
2.1. Adsorbent Materials
2.2. Functional Surface Groups
2.3. Experimental Setup
2.4. Modeling Methods
2.5. Relevant Ligand and Comonomer Reactions
3. Results and Discussion
3.1. Optimization of AO Reaction with AF160 Material
3.2. Prediction of Uranium Uptake for AF1FR3
3.3. Optimization of AO/IDO Ratio for the 38H Material
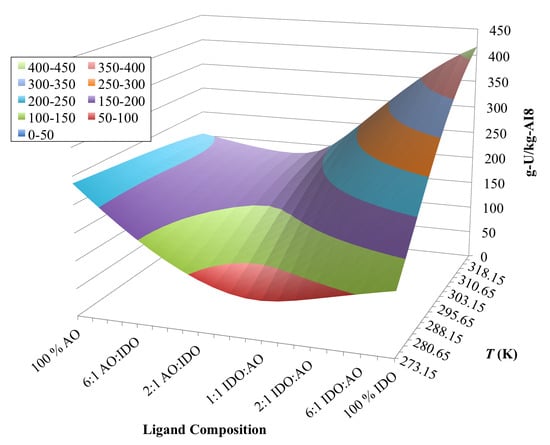
3.4. Optimization of AO/IDO Ratio for AI8 Material
4. Conclusions
Supplementary Materials
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Kim, J.; Tsouris, C.; Mayes, R.T.; Oyola, Y.; Saito, T.; Janke, C.J.; Dai, S.; Schneider, E.; Sachde, D. Recovery of Uranium from Seawater: A Review of Current Status and Future Research Needs. Sep. Sci. Technol. 2013, 48, 367–387. [Google Scholar] [CrossRef]
- Ladshaw, A.; Das, S.; Liao, W.P.; Yiacoumi, S.; Janke, C.; Mayes, R.; Dai, S.; Tsouris, C. Experiments and Modeling of Uranium Uptake by Amidoxime-Based Adsorbents in the Presence of Other Ions in Simulated Seawater. Ind. Eng. Chem. Res. 2016, 55, 4241–4248. [Google Scholar] [CrossRef]
- Kanno, M. Present Status of Study on Extraction of Uranium from Sea Water. J. Nucl. Sci. Technol. 1984, 21, 1–9. [Google Scholar] [CrossRef]
- Rao, L. Recent International R&D Activities in the Extraction of Uranium from Seawater; Report No. LBNL-4034E; Lawrence Berkeley National Laboratory: Berkeley Hills, CA, USA, January 2011.
- Sodaye, H.; Nisan, S.; Poletiko, C.; Prabhakar, S.; Tewari, P.K. Extraction of uranium from the concentrated brine rejected by integrated nuclear desalination plants. Desalination 2009, 235, 9–32. [Google Scholar] [CrossRef]
- Tamada, M. Current status of technology for collection of uranium from seawater. In Proceedings of the International Seminars on Nuclear War and Planetary Emergencies, Erice, Italy, 19–24 August 2009; pp. 243–252. [Google Scholar]
- Seko, N.; Katakai, A.; Hasegawa, S.; Tamada, M.; Kasai, N.; Takeda, H.; Sugo, T.; Saito, K. Aquaculture of Uranium in Seawater by a Fabric-Adsorbent Submerged System. Nucl. Technol. 2003, 144, 274−278. [Google Scholar] [CrossRef]
- U.S. Department of Energy. Nuclear Energy Research and Development Roadmap: Report to Congress; U.S. Department of Energy: Washington, DC, USA, 2010. [Google Scholar]
- Gill, G.; Kuo, L.J.; Strivens, J.; Wood, J.; Schlafer, N. Summary of Adsorption Capacity and Adsorption Kinetics of Uranium and Other Elements on Amidoxime-Based Adsorbents from Time Series Marine Testing at the Pacific Northwest National Laboratory; Report No. PNNL-25899; Pacific Northwest National Laboratory, Marine Sciences Laboratory: Sequim, WA, USA, September 2016.
- Davies, R.V.; Kennedy, J.; McIlroy, R.W.; Spence, R.; Hill, K.M. Extraction of Uranium from Seawater. Nature 1964, 203, 1110–1115. [Google Scholar] [CrossRef]
- Yun, C.K. Development of a Process for Continuous Extraction of Uranium from Seawater; Report No. IAEA-R-1759-F; International Atomic Energy Agency: Vienna, Austria, March 1982. [Google Scholar]
- Ogata, N. Uranium from the sea. Nippon Kaisui Gakkai-Shi. 1976, 30, 3–13. [Google Scholar]
- Gregg, D.; Folkendt, M. Uranium from Seawater; Report No. UCID-19569; Lawrence Livermore National Laboratory: Livermore, CA, USA, September 1982.
- Yamashita, H.; Fujita, K.; Nakajima, F.; Ozawa, Y.; Murata, T. Extraction of Uranium from Seawater Using Magnetic Adsorbents. Sep. Sci. Technol. 1981, 16, 987–998. [Google Scholar] [CrossRef]
- Tabushi, I.; Kobuke, Y.; Nakayama, N.; Aoki, T.; Yoshizawa, A. Chelating Resin Functionalized with Dithiocarbamate for the Recovery of Uranium from Seawater. Ind. Eng. Chem. Prod. Res. Dev. 1984, 23, 445–448. [Google Scholar] [CrossRef]
- Driscoll, M.; Best, F. Systems Studies on the Extraction of Uranium from Seawater; Report No. MIT-EL 81-038; Massachusetts Institute of Technology Press: Boston, MA, USA, November 1981. [Google Scholar]
- Best, F.; Driscoll, M. Prospects for the Recovery of Uranium from Seawater. Nucl. Technol. 1986, 73, 55–68. [Google Scholar] [CrossRef]
- Tabushi, I.; Kobuke, Y.; Nishiya, T. Extraction of uranium from seawater by polymer-bound macrocyclic hexaketone. Nature 1979, 280, 665–666. [Google Scholar] [CrossRef]
- Streeton, R.J.W. Continuous Extraction of Uranium from Sea Water; Report No. AB 15/2806; Atomic Energy Research Establishment: UK National Archives, Harwell, UK, February 1953.
- Williams, W.; Gillam, A. Separation of Uranium from Seawater by Adsorbing Colloid Flotation. Anal. 1978, 103, 1239–1243. [Google Scholar] [CrossRef]
- Kim, Y.; Zeitlin, H. Separation of Uranium from Seawater by Adsorbing Colloid Flotation. Anal. Chem. 1971, 43, 1390–1393. [Google Scholar] [CrossRef] [PubMed]
- Tan, L.; Liu, Q.; Jing, X.; Liu, J.; Song, D.; Hu, S.; Liu, L.; Wang, J. Removal of uranium(VI) ions from aqueous solution by magnetic cobalt ferrite/multiwalled carbon nanotubes composites. Chem. Eng. J. 2015, 273, 301–315. [Google Scholar] [CrossRef]
- Zhou, L.; Shang, C.; Liu, Z.; Huang, G.; Adesina, A. Selective adsorption of uranium(VI) from aqueous solutions using the ion-imprinted magnetic chitosan resins. J. Colloid Interface Sci. 2012, 366, 166–172. [Google Scholar] [CrossRef] [PubMed]
- Sakaguchi, T.; Horikoshi, T.; Akira, N. Uptake of Uranium from sea water by microalgae. J. Ferment. Technol. 1978, 56, 561–565. [Google Scholar]
- Acharya, C.; Chandwadkar, P.; Joseph, D.; Apte, S.K. Uranium (VI) recovery from saline environment by a marine unicellular cyanobacterium, Synechococcus elongates. J. Radioanal. Nucl. Chem. 2013, 295, 845–850. [Google Scholar] [CrossRef]
- Bustard, M.; Donnellan, N.; Rollan, A.; McHale, A. Studies on the biosorption of uranium by a thermotolerant, ethanol-producing strain of Kluyveromyces marxianus. Bioprocess. Biosyst. Eng. 1997, 17, 45–50. [Google Scholar] [CrossRef]
- Zhou, L.; Bosscher, M.; Zhang, C.; Ozcubukcu, S.; Zhang, L.; Zhang, W.; Li, C.; Liu, J.; Jensen, M.; Lai, L.; He, C. A protein engineered to bind uranyl selectively and with femtomolar affinity. Nat. Chem. 2014, 6, 236–241. [Google Scholar] [CrossRef] [PubMed]
- Nakajima, A.; Sakaguchi, T. Recovery and Removal of Uranium by Using Plant Wastes. Biomass 1990, 21, 55–63. [Google Scholar] [CrossRef]
- Nakajima, A.; Sakaguchi, T. Recovery of uranium by tannin immobilized on matrices which have amino group. Chem. Technol. Biotechnol. 1990, 47, 31–38. [Google Scholar] [CrossRef]
- Sakaguchi, T.; Nakajima, A. Recovery of Uranium from Seawater by Immobilized Tannin. Sep. Sci. Technol. 1987, 22, 1609–1623. [Google Scholar] [CrossRef]
- Sugasaka, K.; Katoh, S.; Takai, N.; Takahashi, H.; Umezawa, Y. Recovery of Uranium from Seawater. Sep. Sci. Technol. 1981, 16, 971–985. [Google Scholar] [CrossRef]
- Kobuke, Y.; Tabushi, I.; Aoki, T.; Kamaishi, T.; Hagiwara, I. Composite Fiber Adsorbent for Rapid Uptake of Uranyl from Seawater. Ind. Eng. Chem. Res. 1988, 27, 1461–1466. [Google Scholar] [CrossRef]
- Takeda, T.; Saito, K.; Uezu, K.; Furusaki, S.; Sugo, T.; Okamoto, J. Adsorption and Elution of Hollow-Fiber Packed Bed for Recovery of Uranium from seawater. Ind. Eng. Chem. Res. 1991, 30, 185–190. [Google Scholar] [CrossRef]
- Egawa, H.; Kabay, N.; Shuto, T.; Jyo, A. Recovery of Uranium from Seawater. 14. System Arrangements for the Recovery of Uranium from Seawater by Spherical Amidoxime Chelating Resins Utilizing Natural Seawater Motions. Ind. Eng. Chem. Res. 1993, 32, 709–715. [Google Scholar] [CrossRef]
- Shimizu, T.; Tamada, M. Practical scale system for uranium recovery from seawater using braid type adsorbent. Proc. Civ. Eng. Ocean 2004, 20, 617–622. [Google Scholar] [CrossRef]
- Kim, J.; Oyola, Y.; Tsouris, C.; Hexel, C.; Mayes, R.; Janke, C.; Dai, S. Characterization of Uranium Uptake Kinetics from Seawater in Batch and Flow-Through Experiments. Ind. Eng. Chem. Res. 2013, 52, 9433–9440. [Google Scholar] [CrossRef]
- Kim, J.; Tsouris, C.; Oyola, Y.; Janke, C.; Mayes, R.; Dai, S.; Gill, G.; Kuo, L.J.; Choe, K.Y.; Schneider, E.; et al. Uptake of Uranium from Seawater by Amidoxime-Based Polymeric Adsorbent: Field Experiments, Modeling, and Updated Economic Assessment. Ind. Eng. Chem. Res. 2014, 53, 6076–6083. [Google Scholar] [CrossRef]
- Das, S.; Oyola, Y.; Mayes, R.; Janke, C.; Kuo, L.K.; Gill, G.; Wood, J.; Dai, S. Extracting Uranium from Seawater: Promising AI Series Adsorbents. Ind. Eng. Chem. Res. 2016, 55, 4103–4109. [Google Scholar] [CrossRef]
- Das, S.; Oyola, Y.; Mayes, R.; Janke, C.; Kuo, L.K.; Gill, G.; Wood, J.; Dai, S. Extracting Uranium from Seawater: Promising AF Series Adsorbents. Ind. Eng. Chem. Res. 2016, 55, 4110–4117. [Google Scholar] [CrossRef]
- Brown, S.; Yue, Y.; Kuo, L.K.; Mehio, N.; Li, M.; Gill, G.; Tsouris, C.; Mayes, R.; Saito, T.; Dai, S. Uranium Adsorbent Fibers Prepared by Atom-Transfer Radical Polymerization (ATRP) from Poly(vinyl chloride)-co-chlorinated Poly(vinyl chloride) (PVC-co-CPVC) Fiber. Ind. Eng. Chem. Res. 2016, 55, 4139–4148. [Google Scholar] [CrossRef]
- Das, S.; Liao, W.P.; Byers, M.; Tsouris, C.; Janke, C.; Mayes, R.; Schneider, E.; Kuo, L.J.; Wood, J.; Gill, G.; et al. Alternative Alkaline Conditioning of Amidoxime Based Adsorbent for Uranium Extraction from Seawater. Ind. Eng. Chem. Res. 2016, 55, 4110–4117. [Google Scholar] [CrossRef]
- Na, C.K.; Park, H.J.; Kim, B.G. Optimal amidoximation conditions of acrylonitrile grafted onto polypropylene by photoirradiation-induced graft polymerization. J. Appl. Poly. Sci. 2012, 125, 776–785. [Google Scholar] [CrossRef]
- Gill, G.; Kuo, L.J.; Janke, C.J.; Park, J.; Jeters, R.T.; Bonheyo, G.T.; Pan, H.B.; Wai, C.; Khangaonkar, T.; Bianucci, L.; et al. The Uranium from Seawater Program at the Pacific Northwest National Laboratory: Overview of Marine Testing, Adsorbent Characterization, Adsorbent Durability, Adsorbent Toxicity, and Deployment Studies. Ind. Eng. Chem. Res. 2016, 55, 4264–4277. [Google Scholar] [CrossRef]
- Wu, W.; Priest, C.; Zhou, J.; Peng, C.; Liu, H.; Jiang, D. Solvation of the Ca2UO2(CO3)3 complex in seawater from classical molecular dynamics. J. Phys. Chem. B. 2016, 120, 7227–7233. [Google Scholar] [CrossRef] [PubMed]
- Ansari, S.A.; Yang, Y.; Zhang, Z.; Gagnon, K.J.; Teat, S.J.; Luo, S.; Rao, L. Complexation of lanthanides with glutaroimide-dioxime: binding strength and coordination modes. Inorg. Chem. 2016, 55, 1315–1323. [Google Scholar] [CrossRef] [PubMed]
- Byers, M.E.; Schneider, E. Optimization of the passive recovery of uranium from seawater. Ind. Eng. Chem. Res. 2016, 55, 4351–4361. [Google Scholar] [CrossRef]
- Ivanov, A.S.; Bryantsev, V.S. Assessing ligand selectivity for uranium over vanadium ions to aid in the discovery of superior adsorbents for extraction of UO22+ from seawater. Dalton Trans. 2016, 45, 10744–10751. [Google Scholar] [CrossRef] [PubMed]
- Mehio, N.; Ivanov, A.S.; Ladshaw, A.; Dai, S.; Bryantsev, V.S. Theoretical study of oxovanadium(IV) complexation with formamidoximate: Implications for the design of uranyl-selective adsorbents. Ind. Eng. Chem. Res. 2016, 55, 4231–4240. [Google Scholar] [CrossRef]
- Kuo, L.J.; Janke, C.J.; Wood, J.R.; Strivens, J.E.; Das, S.; Oyola, Y.; Mayes, R.T.; Gill, G.A. Characterization and testing of amidoxime-based adsorbent materials to extract uranium from natural seawater. Ind. Eng. Chem. Res. 2016, 55, 4285–4293. [Google Scholar] [CrossRef]
- Endrizzi, F.; Leggett, C.J.; Rao, L. Scientific Basis for Efficient Extraction of Uranium from Seawater I: understanding the chemical speciation of uranium under seawater conditions. Ind. Eng. Chem. Res. 2016, 55, 4249–4256. [Google Scholar] [CrossRef]
- Ladshaw, A.; Kuo, L.J.; Strivens, J.; Wood, J.; Schlafer, N.; Yiacoumi, S.; Tsouris, C.; Gill, G. Influence of current velocity on uranium adsorption from seawater using an amidoxime-based polymer fiber adsorbent. Ind. Eng. Chem. Res. 2017, 56, 2205–2211. [Google Scholar] [CrossRef]
- Mehio, N.; Williamson, B.; Oyola, Y.; Mayes, R.T.; Janke, C.J.; Brown, S.; Dai, S. Acidity of the Poly (acrylamidoxime) Adsorbent in Aqueous Solution: Determination of the Proton Affinity Distribution via Potentiometric Titrations. Ind. Eng. Chem. Res. 2016, 55, 4217–4223. [Google Scholar] [CrossRef]
- Mehio, N.; Lashely, M.A.; Nugent, J.W.; Tucker, L.; Correia, B.; Do-Thanh, C.L.; Dai, S.; Hancock, R.D.; Bryantsev, V.S. Acidity of the Amidoxime Functional Group in Aqueous Solution: A Combined Experimental and Computational Study. J. Phys. Chem. B. 2015, 119, 3567–3576. [Google Scholar] [CrossRef] [PubMed]
- Brown, S.; Chatterjee, S.; Li, M.; Yue, Y.; Tsouris, C.; Janke, C.J.; Saito, T.; Dai, S. Uranium adsorbent fibers prepared by atom-transfer radical polymerization from chlorinated polypropylene and polyethylene trunk fibers. Ind. Eng. Chem. Res. 2016, 55, 4130–4138. [Google Scholar] [CrossRef]
- Das, S.; Brown, S.; Mayes, R. T.; Janke, C. J.; Tsouris, C.; Kuo, L.J.; Gill, G.; Dai, S. Novel Poly(imide-dioxime) Sorbents: Development and Testing for Enhanced Extraction of Uranium from Natural Seawater. Ind. Eng. Chem. Res. 2016, 298, 125–135. [Google Scholar] [CrossRef]
- Ladshaw, A. Complex Adsorption Modeling for Nuclear Energy Applications. Ph.D. Thesis, Georgia Institute of Technology, Atlanta, GA, USA, May 2017. [Google Scholar]
- Westall, J.C.; Morel, F.M.M.; Zachary, J.L. MINEQL: A Computer Program for the Calculation of Chemical Equilibrium Composition of Aqueous Systems; Massachusetts Institute of Technology: Cambridge, MA, USA, 1976; Volume 176, p. 8. [Google Scholar]
- Schecher, W.D.; McAvoy, D.C. MINEQL+: A Software Environment for Chemical Equilibrium Modeling. Comput. Environ. Urban Syst. 1992, 16, 65–76. [Google Scholar] [CrossRef]
- Benjamin, M.M. Water Chemistry, 1st ed.; Waveland Press Inc.: Long Grove, IL, USA, 2010; ISBN 978-1-57766-667-7. [Google Scholar]
- Yiacoumi, S.; Tien, C. Kinetics of Metal Ion Adsorption from Aqueous Solutions; Kluwer Academic Publishers: Boston, MA, USA, 1995; ISBN 978-1-4615-2319-2. [Google Scholar]
- Tien, C. Adsorption Calculations and Modeling; Butterworth-Heinemann: Boston, MA, USA, 1994; ISBN 978-0-7506-9121-5. [Google Scholar]
- Kalinin, V.V.; Radke, C.J. An ion-binding model for ionic surfactant adsorption at aqueous-fluid interfaces. Colloids Surf. 1996, 114, 337–350. [Google Scholar] [CrossRef]
- Tian, G.; Teat, S.J.; Zhang, Z.; Rao, L. Sequestering uranium from seawater: binding strength and modes of uranyl complexes with glutarimidedioxime. Dalton Trans. 2012, 41, 11579–11586. [Google Scholar] [CrossRef] [PubMed]
- Lashley, M.A.; Mehio, N.; Nugent, J.W.; Holguin, E.; Do-Thanh, C.L.; Bryantsev, V.S.; Dai, S.; Hancock, R.D. Amidoximes as Ligand Functionalities for Braided Polymeric Materials for the Recovery of Uranium from Seawater. Polyhedron 2016, 109, 81–91. [Google Scholar] [CrossRef]
- Leggett, C.J.; Endrizzi, F.; Rao, L. Scientific Basis for Efficient Extraction of Uranium from Seawater II: Fundamental Thermodynamics and Structural Studies. Ind. Eng. Chem. Res. 2016, 55, 4257–4263. [Google Scholar] [CrossRef]
- Davies, C.W. Ion Association, 1st ed.; Butterworths: Washington, DC, USA, 1962. [Google Scholar]
- Grahame, D.C. The Electrical Double Layer and the Theory of Electrocapillarity. Chem. Rev. 1947, 41, 441–500. [Google Scholar] [CrossRef] [PubMed]
- Tian, G.; Teat, S.J.; Zhang, Z.; Rao, L. “Thermodynamic studies of U(VI) complexation with glutardiamidoxime for sequestration of uranium from seawater”. Dalton Trans. 2013, 42, 5690–5696. [Google Scholar] [CrossRef] [PubMed]
- OECD SIDS, Methacrylic Acid, UNEP Publications, CAS No. 79-41-4. Available online: www.inchem.org/documents/sids/sids/79414.pdf (accessed on 9 September 2017).
- Bingӧl, B. Synthesis and Characterization of Poly(vinylphonphonic acid) for Proton Exchange Membranes in Fuel Cells. Ph.D. Thesis, Johannes Gutenberg University of Mainz, Mainz, Germany, May 2007. [Google Scholar]
- Haynes, W.M. CRC Handbook of Chemistry and Physics, 91st ed.; Taylor and Francis: Oxford, UK, 2010; ISBN 978-1439820773. [Google Scholar]
- Astheimer, L.; Schenk, H.J.; Witte, E.G.; Schwochau, K. Development of Sorbers for the Recovery of Uranium from Seawater by Resins Containing Amidoxime and Imidoxime Functional Groups. Sep. Sci. Technol. 1983, 18, 367. [Google Scholar] [CrossRef]
- Zheng, B.; Cai, S.; Zhuang, M.; Jiang, L. Mechanisms of Uranium Adsorption on Amidoxime Resin. Acta Ocean. Sin. 1985, 2, 417. [Google Scholar]
- Sekiguchi, K.; Saito, K.; Konishi, S.; Furusaki, S.; Sugo, T.; Nobukawa, H. Effect of Seawater Temperature on Uranium Recovery from Seawater Using Amidoxime Adsorbents. Ind. Eng. Chem. Res. 1994, 33, 662. [Google Scholar] [CrossRef]
- Braase, L.; May, W.E. Fuel Cycle Technologies Annual Meeting Transactions; Report No. INL/EXT-14-33501; Idaho National Laboratory: Idaho Falls, ID, USA, October 2014.
- US EIA. 2016 Uranium Marketing Annual Report. US DOE, June 2017. Available online: https://www.eia.gov/uranium/marketing/pdf/2016umar.pdf (Accessed on 26 October 2017).










| Sample ID | Primary Elements (wt %) | |||
|---|---|---|---|---|
| C | H | N | O | |
| PE hollow gear fiber | 84.9 | 14.5 | <0.5 | <0.5 |
| Grafted 38H | 62.3 | 7.8 | 12.6 | 15.8 |
| Amidoximated 38H | 49.9 | 7.2 | 13.8 | 24.0 |
| Adsorbent | Comonomer | N Concentration (mol/kg) | Comonomer Concentration (mol/kg) |
|---|---|---|---|
| 38H | MAA | 9.9 | 5.5 |
| AI8 | VPA | 8.7 * | 2.5 * |
| AF1 | ITA | 12.8 | 2.0 |
| Chemisorption Reactions | ΔG (kJ/mol) | ΔH (kJ/mol) | ΔS (J/K/mol) |
|---|---|---|---|
| Acetamidoxime (AO): | |||
| UO22+ + AO− ⇆ UO2(AO)+ | −77.6 a | ||
| UO22+ + 2AO− ⇆ UO2(AO)2 | −135.3 a | −242.9 b | −329 b |
| UO22+ + 3AO− ⇆ UO2(AO)3− | −159.3 c | ||
| UO22+ + AO− + CO32− ⇆ UO2(AO)(CO3)− | −90.2 c | ||
| UO22+ + 2AO− + CO32− ⇆ UO2(AO)2(CO3)2− | −145.6 c | ||
| Glutarimide-Dioxime (IDO): | |||
| UO22+ + HIDO2− ⇆ UO2(HIDO) | −109.6 d | −67.3 d | 142 d |
| UO22+ + H+ + HIDO2− ⇆ UO2(H2IDO)+ | −134.1 d | −75.4 d | 197 d |
| UO22+ + 2HIDO2− ⇆ UO2(HIDO)22− | −165.5 d | −109.0 d | 188 d |
| UO22+ + H+ + 2HIDO2− ⇆ UO2(H2IDO)(HIDO)− | −222.0 d | −130.0 d | 309 d |
| UO22+ + 2H+ + 2HIDO2− ⇆ UO2(H2IDO)2 | −252.3 d | −161.0 d | 307 d |
| UO22+ + HIDO2− + CO32− ⇆ UO2(HIDO)(CO3)2− | −143.8 c | ||
| UO22+ + H+ + HIDO2− + CO32− ⇆ UO2(H2IDO)(CO3)− | −166.7 | ||
| Protonation/Deprotonation Reaction | pKa | ΔG (kJ/mol) |
|---|---|---|
| H2AO+ ⇆ HAO + H+ | 5.8 | 33.0 |
| HAO ⇆ AO− + H+ | 13.2 | 75.4 |
| H4IDO+ ⇆ H3IDO + H+ | 2.1 | 12.1 |
| H3IDO ⇆ H2IDO− + H+ | 11.0 | 63.4 |
| H2IDO− ⇆ HIDO2− + H+ | 12.9 | 73.3 |
| HMAA ⇆ MAA− + H+ | 4.7 | 26.2 * |
| H2VPA ⇆ HVPA− + H+ | 2.7 | 15.4 * |
| HVPA− ⇆ VPA2− + H+ | 7.3 | 41.2 * |
| H2ITA ⇆ HITA− + H+ | 3.9 | 22.0 |
| HITA− ⇆ ITA2− + H+ | 5.5 | 31.1 |
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ladshaw, A.P.; Wiechert, A.I.; Das, S.; Yiacoumi, S.; Tsouris, C. Amidoxime Polymers for Uranium Adsorption: Influence of Comonomers and Temperature. Materials 2017, 10, 1268. https://doi.org/10.3390/ma10111268
Ladshaw AP, Wiechert AI, Das S, Yiacoumi S, Tsouris C. Amidoxime Polymers for Uranium Adsorption: Influence of Comonomers and Temperature. Materials. 2017; 10(11):1268. https://doi.org/10.3390/ma10111268
Chicago/Turabian StyleLadshaw, Austin P., Alexander I. Wiechert, Sadananda Das, Sotira Yiacoumi, and Costas Tsouris. 2017. "Amidoxime Polymers for Uranium Adsorption: Influence of Comonomers and Temperature" Materials 10, no. 11: 1268. https://doi.org/10.3390/ma10111268
APA StyleLadshaw, A. P., Wiechert, A. I., Das, S., Yiacoumi, S., & Tsouris, C. (2017). Amidoxime Polymers for Uranium Adsorption: Influence of Comonomers and Temperature. Materials, 10(11), 1268. https://doi.org/10.3390/ma10111268