Mesoscale Anisotropy in Porous Media Made of Clay Minerals. A Numerical Study Constrained by Experimental Data
Abstract
:1. Introduction
2. Materials and Methods
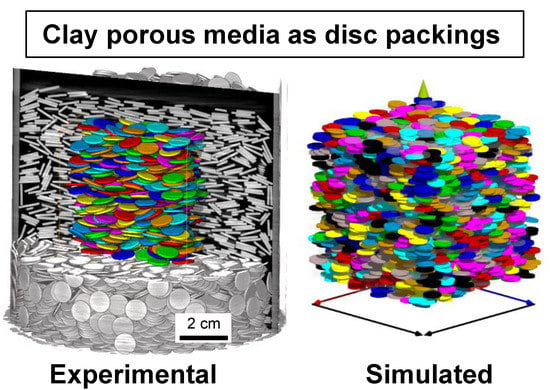
2.1. Simulation of 3D Disk Packings
2.2. Experimental Disk Packings
2.2.1. Experimental Setup and Preparation of Disk Packings
2.2.2. X-Ray Microtomography Analyses
3. Results and Discussion
3.1. Evolution of Simulated and Experimental Porosity with Packing Anisotropy
3.2. Comparison between Simulated and Experimental Orientation Distribution Functions
3.3. Evolution of Geometrical Properties of Simulated Porous Media with Anisotropy
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Altmann, S.; Tournassat, C.; Goutelard, F.; Parneix, J.C.; Gimmi, T.; Maes, N. Diffusion-driven transport in clayrock formations. Appl. Geochem. 2012, 27, 463–478. [Google Scholar] [CrossRef]
- Aristilde, L.; Galdi, S.M.; Kelch, S.E.; Aoki, T.G. Sugar-influenced water diffusion, interaction, and retention in clay interlayer nanopores probed by theoretical simulations and experimental spectroscopies. Adv. Water Resour. 2017, 106, 24–38. [Google Scholar] [CrossRef]
- Gu, X.; Sun, J.; Evans, L.J. The development of a multi-surface soil speciation model for Cd (II) and Pb (II): Comparison of two approaches for metal adsorption to clay fractions. Appl. Geochem. 2014, 47, 99–108. [Google Scholar] [CrossRef]
- Leu, L.; Georgiadis, A.; Blunt, M.; Busch, A.; Bertier, P.; Schweinar, K.; Liebi, M.; Menzel, A.; Ott, H. Multiscale description of shale pore systems by scanning SAXS and WAXS microscopy. Energy Fuels 2016, 30, 10282–10297. [Google Scholar]
- Czurda, K.A.; Wagner, J.F. Cation transport and retardation processes in view of the toxic waste deposition problem in clay rocks and clay liner encapsulation. Eng. Geol. 1991, 30, 103–113. [Google Scholar]
- Harvey, C.; Lagaly, G. Industrial applications. In Developments in Clay Science; Elsevier: Amsterdam, The Netherlands, 2013; pp. 451–490. ISBN 978-0-08-099364-5. [Google Scholar]
- Lee, J.M.; Shackelford, C.D.; Benson, C.H.; Jo, H.Y.; Edil, T.B. Correlating index properties and hydraulic conductivity of geosynthetic clay liners. J. Geotech. Geoenviron. Eng. 2005, 131, 1319–1329. [Google Scholar] [CrossRef]
- Madsen, F. Clay mineralogical investigations related to nuclear waste disposal. Clay Miner. 1998, 33, 109–129. [Google Scholar]
- Ortiz, L.; Volckaert, G.; Mallants, D. Gas generation and migration in Boom Clay, a potential host rock formation for nuclear waste storage. Eng. Geol. 2002, 64, 287–296. [Google Scholar] [CrossRef]
- Roehl, K.E.; Czurda, K. Diffusion and solid speciation of Cd and Pb in clay liners. Appl. Clay Sci. 1998, 12, 387–402. [Google Scholar] [CrossRef]
- Brigatti, M.; Galan, E.; Theng, B. Structure and mineralogy of clay minerals. In Developments in Clay Science; Elsevier: Amsterdam, The Netherlands, 2013; pp. 21–81. ISBN 978-0-08-099364-5. [Google Scholar]
- Dias, N.M.; Gonçalves, D.; Leite, W.C.; Brinatti, A.M.; Saab, S.C.; Pires, L.F. Morphological characterization of soil clay fraction in nanometric scale. Powder Technol. 2013, 241, 36–42. [Google Scholar] [CrossRef]
- Gélinas, V.; Vidal, D. Determination of particle shape distribution of clay using an automated AFM image analysis method. Powder Technol. 2010, 203, 254–264. [Google Scholar] [CrossRef]
- Hubert, F.; Caner, L.; Meunier, A.; Ferrage, E. Unraveling complex <2 μm clay mineralogy from soils using X-ray diffraction profile modeling on particle-size sub-fractions: Implications for soil pedogenesis and reactivity. Am. Mineral. 2012, 97, 384–398. [Google Scholar]
- Reinholdt, M.X.; Hubert, F.; Faurel, M.; Tertre, E.; Razafitianamaharavo, A.; Francius, G.; Prêt, D.; Petit, S.; Béré, E.; Pelletier, M. Morphological properties of vermiculite particles in size-selected fractions obtained by sonication. Appl. Clay Sci. 2013, 77, 18–32. [Google Scholar] [CrossRef]
- Bacle, P.; Dufrêche, J.F.; Rotenberg, B.; Bourg, I.C.; Marry, V. Modeling the transport of water and ionic tracers in a micrometric clay sample. Appl. Clay Sci. 2016, 123, 18–28. [Google Scholar] [CrossRef] [Green Version]
- Ebrahimi, D.; Pellenq, R.J.M.; Whittle, A.J. Mesoscale simulation of clay aggregate formation and mechanical properties. Granul. Matter 2016, 18, 49. [Google Scholar] [CrossRef]
- Ferrage, E.; Hubert, F.; Tertre, E.; Delville, A.; Michot, L.J.; Levitz, P. Modeling the arrangement of particles in natural swelling-clay porous media using three-dimensional packing of elliptic disks. Phys. Rev. E 2015, 91, 062210. [Google Scholar] [CrossRef] [PubMed]
- Tyagi, M.; Gimmi, T.; Churakov, S.V. Multi-scale micro-structure generation strategy for up-scaling transport in clays. Adv. Water Resour. 2013, 59, 181–195. [Google Scholar] [CrossRef]
- Backeberg, N.R.; Iacoviello, F.; Rittner, M.; Mitchell, T.M.; Jones, A.P.; Day, R.; Wheeler, J.; Shearing, P.R.; Vermeesch, P.; Striolo, A. Quantifying the anisotropy and tortuosity of permeable pathways in clay-rich mudstones using models based on X-ray tomography. Sci. Rep. 2017, 7, 14838. [Google Scholar] [CrossRef] [PubMed]
- Greenkorn, R.; Johnson, C.; Shallenberger, L. Directional permeability of heterogeneous anisotropic porous media. Soc. Pet. Eng. J. 1964, 4, 124–132. [Google Scholar] [CrossRef]
- Jacops, E.; Aertsens, M.; Maes, N.; Bruggeman, C.; Krooss, B.; Amann-Hildenbrand, A.; Swennen, R.; Littke, R. Interplay of molecular size and pore network geometry on the diffusion of dissolved gases and HTO in Boom Clay. Appl. Geochem. 2017, 76, 182–195. [Google Scholar] [CrossRef]
- Van Loon, L.R.; Soler, J.M.; Müller, W.; Bradbury, M.H. Anisotropic diffusion in layered argillaceous rocks: A case study with Opalinus Clay. Environ. Sci. Technol. 2004, 38, 5721–5728. [Google Scholar] [CrossRef] [PubMed]
- Aplin, A.C.; Matenaar, I.F.; McCarty, D.K.; van Der Pluijm, B.A. Influence of mechanical compaction and clay mineral diagenesis on the microfabric and pore-scale properties of deep-water Gulf of Mexico mudstones. Clays Clay Miner. 2006, 54, 500–514. [Google Scholar] [CrossRef]
- Vasseur, G.; Djeran-Maigre, I.; Grunberger, D.; Rousset, G.; Tessier, D.; Velde, B. Evolution of structural and physical parameters of clays during experimental compaction. Mar. Pet. Geol. 1995, 12, 941–954. [Google Scholar] [CrossRef]
- Zhang, S.; Tullis, T.E.; Scruggs, V.J. Permeability anisotropy and pressure dependency of permeability in experimentally sheared gouge materials. J. Struct. Geol. 1999, 21, 795–806. [Google Scholar] [CrossRef]
- Chen, X.; Verma, R.; Nicolas Espinoza, D.; Prodanović, M. Pore-scale determination of gas relative permeability in hydrate-bearing sediments using X-ray computed micro-tomography and lattice boltzmann method. Water Resour. Res. 2018, 54, 600–608. [Google Scholar] [CrossRef]
- Gaboreau, S.; Robinet, J.C.; Pret, D. Optimization of pore-network characterization of a compacted clay material by TEM and FIB/SEM imaging. Microporous Mesoporous Mater. 2016, 224, 116–128. [Google Scholar] [CrossRef]
- Hemes, S.; Desbois, G.; Urai, J.L.; Schröppel, B.; Schwarz, J.O. Multi-scale characterization of porosity in Boom Clay (HADES-level, Mol, Belgium) using a combination of X-ray μ-CT, 2D BIB-SEM and FIB-SEM tomography. Microporous Mesoporous Mater. 2015, 208, 1–20. [Google Scholar] [CrossRef]
- Houben, L.; Sadan, M.B. Refinement procedure for the image alignment in high-resolution electron tomography. Ultramicroscopy 2011, 111, 1512–1520. [Google Scholar] [CrossRef] [PubMed]
- Ebrahimi, D.; Whittle, A.J.; Pellenq, R.J.M. Effect of polydispersity of clay platelets on the aggregation and mechanical properties of clay at the mesoscale. Clays Clay Miner. 2016, 64, 335–347. [Google Scholar] [CrossRef]
- Ebrahimi, D.; Whittle, A.J.; Pellenq, R.J.M. Mesoscale properties of clay aggregates from potential of mean force representation of interactions between nanoplatelets. J. Chem. Phys. 2014, 140, 154309. [Google Scholar] [CrossRef] [Green Version]
- Ho, T.A.; Greathouse, J.A.; Wang, Y.; Criscenti, L.J. Atomistic structure of mineral nano-aggregates from simulated compaction and dewatering. Sci. Rep. 2017, 7, 15286. [Google Scholar] [CrossRef] [PubMed]
- Coelho, D.; Thovert, J.F.; Adler, P. Geometrical and transport properties of random packings of spheres and aspherical particles. Phys. Rev. E 1997, 55, 1959–1978. [Google Scholar] [CrossRef]
- Jia, T.; Zhang, Y.; Chen, J. Simulation of granular packing of particles with different size distributions. Comput. Mater. Sci. 2012, 51, 172–180. [Google Scholar] [CrossRef]
- Hubert, F.; Bihannic, I.; Prêt, D.; Tertre, E.; Nauleau, B.; Pelletier, M.; Demé, B.; Ferrage, E. Investigating the anisotropic features of particle orientation in synthetic swelling clay porous media. Clays Clay Miner. 2013, 61, 397–415. [Google Scholar] [CrossRef]
- Hassan, M.S.; Villieras, F.; Gaboriaud, F.; Razafitianamaharavo, A. AFM and low-pressure argon adsorption analysis of geometrical properties of phyllosilicates. J. Colloid Interface Sci. 2006, 296, 614–623. [Google Scholar] [CrossRef] [PubMed]
- Chaikin, P.M.; Lubensky, T.C. Principles of Condensed Matter Physics; Cambridge University Press: Cambridge, UK, 2000. [Google Scholar]
- Eppenga, R.; Frenkel, D. Monte Carlo study of the isotropic and nematic phases of infinitely thin hard platelets. Mol. Phys. 1984, 52, 1303–1334. [Google Scholar] [CrossRef]
- Hermans, P.H.; Platzek, P. Beiträge zur Kenntnis des Deformationsmechanismus und der Feinstruktur der Hydratzellulose. Kolloid Z. 1939, 88, 73–78. (In German) [Google Scholar] [CrossRef]
- Méheust, Y.; Knudsen, K.D.; Fossum, J.O. Inferring orientation distributions in anisotropic powders of nano-layered crystallites from a single two-dimensional WAXS image. J. Appl. Crystallogr. 2006, 39, 661–670. [Google Scholar] [CrossRef] [Green Version]
- Meng, L.; Jiao, Y.; Li, S. Maximally dense random packings of spherocylinders. Powder Technol. 2016, 292, 176–185. [Google Scholar] [CrossRef]
- Perdigon-Aller, A.C.; Aston, M.; Clarke, S.M. Preferred orientation in filtercakes of kaolinite. J. Colloid Interface Sci. 2005, 290, 155–165. [Google Scholar] [CrossRef] [PubMed]
- Callahan, J. A nontoxic heavy liquid and inexpensive filters for separation of mineral grains. J. Sediment. Res. 1987, 57, 765–766. [Google Scholar] [CrossRef]
- Gregory, M.R.; Johnston, K.A. A nontoxic substitute for hazardous heavy liquids—aqueous sodium polytungstate (3Na2WO4·9WO3·H2O) solution (Note). N. Z. J. Geol. Geophys. 1987, 30, 317–320. [Google Scholar] [CrossRef]
- Kak, A.; Slaney, M. Principles of Computerized Tomographic Imaging; SIAM: Philadelphia, PA, USA, 2001. [Google Scholar]
- Russ, J.C. The Image Processing. Handbook, 6th ed.; CRC Press: Boca Raton, FL, USA, 2011. [Google Scholar]
- Soille, P. Morphological Image Analysis: Principles and Applications; Springer: Berlin, Germany, 2004. [Google Scholar]
- Cleary, P.W.; Sawley, M.L. DEM modelling of industrial granular flows: 3D case studies and the effect of particle shape on hopper discharge. Appl. Math. Model. 2002, 26, 89–111. [Google Scholar] [CrossRef]
- Fraige, F.Y.; Langston, P.A.; Chen, G.Z. Distinct element modelling of cubic particle packing and flow. Powder Technol. 2008, 186, 224–240. [Google Scholar] [CrossRef]
- Li, J.; Langston, P.A.; Webb, C.; Dyakowski, T. Flow of sphero-disc particles in rectangular hoppers—A DEM and experimental comparison in 3D. Chem. Eng. Sci. 2004, 59, 5917–5929. [Google Scholar] [CrossRef]
- Kim, J.H.; Ochoa, J.A.; Whitaker, S. Diffusion in anisotropic porous media. Transp. Porous Media 1987, 2, 327–356. [Google Scholar] [CrossRef]
- Mammar, N.; Rosanne, M.; Prunet-Foch, B.; Thovert, J.F.; Tevissen, E.; Adler, P. Transport properties of compact clays: I. Conductivity and permeability. J. Colloid Interface Sci. 2001, 240, 498–508. [Google Scholar] [CrossRef] [PubMed]
- Cavallaro, G.; Lazzara, G.; Milioto, S.; Palmisano, G.; Parisi, F. Halloysite nanotube with fluorinated lumen: Non-foaming nanocontainer for storage and controlled release of oxygen in aqueous media. J. Colloid Interface Sci. 2014, 417, 66–71. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Lisuzzo, L.; Cavallaro, G.; Parisi, F.; Milioto, S.; Lazzara, G. Colloidal stability of halloysite clay nanotubes. Ceram. Int. 2018, in press. [Google Scholar] [CrossRef]
- Ketcham, R.A.; Slottke, D.T.; Sharp, J.M., Jr. Three-dimensional measurement of fractures in heterogeneous materials using high-resolution X-ray computed tomography. Geosphere 2010, 6, 499–514. [Google Scholar] [CrossRef] [Green Version]
- Bunge, H.J. Texture Analysis in Materials Science: Mathematical Methods; Elsevier: Amsterdam, The Netherlands, 2013. [Google Scholar]
- Labarthet, F.L.; Buffeteau, T.; Sourisseau, C. Orientation distribution functions in uniaxial systems centered perpendicularly to a constraint direction. Appl. Spectrosc. 2000, 54, 699–705. [Google Scholar] [CrossRef]
- Cousin, I.; Levitz, P.; Bruand, A. Three-dimensional analysis of a loamy-clay soil using pore and solid chord distributions. Eur. J. Soil Sci. 1996, 47, 439–452. [Google Scholar] [CrossRef]
- Levitz, P.; Tchoubar, D. Disordered porous solids: From chord distributions to small angle scattering. J. Phys. I 1992, 2, 771–790. [Google Scholar] [CrossRef]
- Rozenbaum, O. 3-D characterization of weathered building limestones by high resolution synchrotron X-ray microtomography. Sci. Total Environ. 2011, 409, 1959–1966. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Torquato, S.; Lu, B. Chord-length distribution function for two-phase random media. Phys. Rev. E 1993, 47, 2950. [Google Scholar] [CrossRef]
- Davidson, P.; Petermann, D.; Levelut, A.M. The measurement of the nematic order parameter by X-ray scattering reconsidered. J. Phys. II 1995, 5, 113–131. [Google Scholar] [CrossRef]
- Lemaire, B.; Panine, P.; Gabriel, J.; Davidson, P. The measurement by SAXS of the nematic order parameter of laponite gels. EPL Europhys. Lett. 2002, 59, 55. [Google Scholar] [CrossRef]
- Sanchez-Castillo, A.; Osipov, M.A.; Giesselmann, F. Orientational order parameters in liquid crystals: A comparative study of X-ray diffraction and polarized Raman spectroscopy results. Phys. Rev. E 2010, 81, 021707. [Google Scholar] [CrossRef] [PubMed]







| Sample | DP1 | DP2 | DP3 | DP4 | DP5 |
|---|---|---|---|---|---|
| Fluid | Air | Water | Na-polytungstate | Na-polytungstate | Na polytungstate |
| Density | 10−3 | 1.00 | 2.10 | 2.15 | 2.15 |
| Drop-off | Individual | Individual | Individual | Individual | All at once |
| ε | 0.48 | 0.47 | 0.49 | 0.54 | 0.51 |
| S | 0.96 | 0.97 | 0.91 | 0.90 | 0.84 |
| Initial Angle | Max. Swivel Amplitude (°) | Max. Slide Amplitude (µm) | S | ε | Npart. | fpart. |
|---|---|---|---|---|---|---|
| 82 | 11 | d/6.4 | 0.00 | 0.73 | 2.28 | 0.34 |
| 87 | 22 | d/7 | 0.10 | 0.70 | 2.33 | 0.42 |
| 87 | 25 | d/2 | 0.20 | 0.67 | 2.42 | 0.47 |
| 85 | 40 | d/7 | 0.31 | 0.66 | 2.48 | 0.51 |
| 89 | 50 | d/7 | 0.42 | 0.64 | 2.55 | 0.56 |
| 82 | 60 | d/2 | 0.52 | 0.62 | 2.69 | 0.59 |
| 85 | 85 | d/3 | 0.60 | 0.60 | 2.80 | 0.65 |
| 85 | 80 | d | 0.69 | 0.59 | 2.85 | 0.63 |
| 60 | 60 | d | 0.81 | 0.57 | 2.91 | 0.69 |
| 47 | 28 | d/3 | 0.84 | 0.58 | 2.90 | 0.67 |
| 40 | 40 | d | 0.89 | 0.55 | 3.06 | 0.73 |
| 25 | 45 | d/2 | 0.92 | 0.54 | 3.09 | 0.74 |
| 18 | 55 | d | 0.94 | 0.53 | 3.16 | 0.76 |
| 10 | 70 | 4d | 0.96 | 0.49 | 3.63 | 0.83 |
| 0 | 80 | 5d | 0.98 | 0.45 | 3.91 | 0.87 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Dabat, T.; Mazurier, A.; Hubert, F.; Tertre, E.; Grégoire, B.; Dazas, B.; Ferrage, E. Mesoscale Anisotropy in Porous Media Made of Clay Minerals. A Numerical Study Constrained by Experimental Data. Materials 2018, 11, 1972. https://doi.org/10.3390/ma11101972
Dabat T, Mazurier A, Hubert F, Tertre E, Grégoire B, Dazas B, Ferrage E. Mesoscale Anisotropy in Porous Media Made of Clay Minerals. A Numerical Study Constrained by Experimental Data. Materials. 2018; 11(10):1972. https://doi.org/10.3390/ma11101972
Chicago/Turabian StyleDabat, Thomas, Arnaud Mazurier, Fabien Hubert, Emmanuel Tertre, Brian Grégoire, Baptiste Dazas, and Eric Ferrage. 2018. "Mesoscale Anisotropy in Porous Media Made of Clay Minerals. A Numerical Study Constrained by Experimental Data" Materials 11, no. 10: 1972. https://doi.org/10.3390/ma11101972
APA StyleDabat, T., Mazurier, A., Hubert, F., Tertre, E., Grégoire, B., Dazas, B., & Ferrage, E. (2018). Mesoscale Anisotropy in Porous Media Made of Clay Minerals. A Numerical Study Constrained by Experimental Data. Materials, 11(10), 1972. https://doi.org/10.3390/ma11101972