Thermal Properties of SiOC Glasses and Glass Ceramics at Elevated Temperatures
Abstract
:1. Introduction
2. Experimental Procedure
3. Results and Discussion
3.1. Chemical and Microstructural Characterization of SiOC Samples
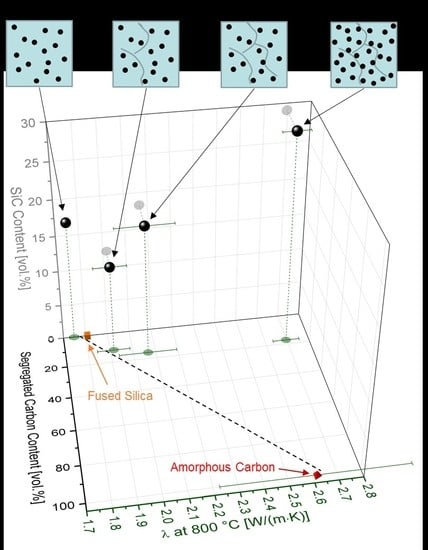
3.2. Thermal Properties of SiOC Glasses and Glass Ceramics
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Widgeon, S.J.; Sen, S.; Mera, G.; Ionescu, E.; Riedel, R.; Navrotsky, A. 29Si and 13C solid-state NMR spectroscopic study of nanometer-scale structure and mass fractal characteristics of amorphous polymer-derived silicon oxycarbide ceramics. Chem. Mater. 2010, 22, 6221–6228. [Google Scholar] [CrossRef]
- Colombo, P.; Mera, G.; Riedel, R.; Sorarù, G.D. Polymer-derived ceramics: 40 Years of research and innovation in advanced ceramics. J. Am. Ceram. Soc. 2010, 93, 1805–1837. [Google Scholar] [CrossRef]
- Soraru, G.D.; D’Andrea, G.; Campostrini, R.; Babonneau, F.; Mariotto, G. Structural characterization and high-temperature behavior of silicon oxycarbide glasses prepared from sol-gel precursors containing Si-H bonds. J. Am. Ceram. Soc. 1995, 78, 379–387. [Google Scholar] [CrossRef]
- Pantano, C.G.; Singh, A.K.; Zhang, H. Silicon oxycarbide glasses. J. Sol-Gel Sci. Technol. 1999, 14, 7–25. [Google Scholar] [CrossRef]
- Soraru, G.D. Silicon oxycarbide glasses from gels. J. Sol-Gel Sci. Technol. 1994, 2, 843–848. [Google Scholar] [CrossRef]
- Bois, L.; Maquet, J.; Babonneau, F.; Bahloul, D. Structural Characterization of Sol-Gel Derived Oxycarbide Glasses. 2. Study of the Thermal Stability of the Silicon Oxycarbide Phase. Chem. Mater. 1995, 7, 975–981. [Google Scholar] [CrossRef]
- Soraru, G.D.; Modena, S.; Guadagnino, E.; Colombo, P.; Egan, J.; Pantano, C. Chemical durability of silicon oxycarbide glasses. J. Am. Ceram. Soc. 2002, 85, 1529–1536. [Google Scholar] [CrossRef]
- Gregori, G.; Kleebe, H.-J.; Blum, Y.D.; Babonneau, F. Evolution of C-rich SiOC ceramics: Part II. Characterization by high lateral resolution techniques: Electron energy-loss spectroscopy, high-resolution TEM and energy-filtered TEM. Int. J. Mater. Res. 2006, 97, 710–720. [Google Scholar] [CrossRef]
- Saha, A.; Raj, R. Crystallization maps for SiCO amorphous ceramics. J. Am. Ceram. Soc. 2007, 90, 578–583. [Google Scholar] [CrossRef]
- Brequel, H.; Parmentier, J.; Walter, S.; Badheka, R.; Trimmel, G.; Masse, S.; Latournerie, J.; Dempsey, P.; Turquat, C.; Desmartin-Chomel, A.; et al. Systematic Structural Characterization of the High-Temperature Behavior of Nearly Stoichiometric Silicon Oxycarbide Glasses. Chem. Mater. 2004, 16, 2585–2598. [Google Scholar] [CrossRef]
- Hurwitz, F.I.; Heimann, P.; Farmer, S.C.; Hembree, D.M., Jr. Characterization of the pyrolytic conversion of polysilsesquioxanes to silicon oxycarbides. J. Mater. Sci. 1993, 28, 6622–6630. [Google Scholar] [CrossRef]
- Brewer, C.M.; Bujalski, D.R.; Parent, V.E.; Su, K.; Zank, G.A. Insights into the oxidation chemistry of SiOC ceramics derived from silsesquioxanes. J. Sol-Gel Sci. Technol. 1999, 14, 49–68. [Google Scholar] [CrossRef]
- Renlund, G.M.; Prochazka, S.; Doremus, R.H. Silicon oxycarbide glasses. Part II. Structure and properties. J. Mater. Res. 1991, 6, 2723–2734. [Google Scholar] [CrossRef]
- Rouxel, T.; Massouras, G.; Soraru, G.-D. High temperature behavior of a gel-derived SiOC glass: Elasticity and viscosity. J. Sol-Gel Sci. Technol. 1999, 14, 87–94. [Google Scholar] [CrossRef]
- Reitz, E.; Schell, K.G.; Bucharsky, E.C.; Oberacker, R.; Hoffmann, M.J. Precursor derived SiOC/MoSi2-composites for diesel glow plugs: Preparation and high temperature properties. J. Ceram. Soc. Jpn. 2016, 124, 1017–1022. [Google Scholar] [CrossRef]
- Harshe, R.; Balan, C.; Riedel, R. Amorphous Si(Al)OC ceramic from polysiloxanes: Bulk ceramic processing, crystallization behavior and applications. J. Eur. Ceram. Soc. 2004, 24, 3471–3482. [Google Scholar] [CrossRef]
- Fedorova, A.; Michelsen, L.; Scheffler, M. Polymer-derived ceramic tapes with small and negative thermal expansion coefficients. J. Eur. Ceram. Soc. 2018, 38, 719–725. [Google Scholar] [CrossRef]
- Mazo, M.A.; Palencia, C.; Nistal, A.; Rubio, F.; Rubio, J.; Oteo, J.L. Dense bulk silicon oxycarbide glasses obtained by spark plasma sintering. J. Eur. Ceram. Soc. 2012, 32, 3369–3378. [Google Scholar] [CrossRef]
- Mazo, M.A.; Tamayo, A.; Caballero, A.C.; Rubio, J. Electrical and thermal response of silicon oxycarbide materials obtained by spark plasma sintering. J. Eur. Ceram. Soc. 2017, 37, 2011–2020. [Google Scholar] [CrossRef]
- Eom, J.-H.; Kim, Y.-W.; Kim, K.J.; Seo, W.-S. Improved electrical and thermal conductivities of polysiloxane-derived silicon oxycarbide ceramics by barium addition. J. Eur. Ceram. Soc. 2018, 38, 487–493. [Google Scholar] [CrossRef]
- Gurlo, A.; Ionescu, E.; Riedel, R.; Clarke, D.R. The Thermal Conductivity of Polymer-Derived Amorphous Si-O-C Compounds and Nano-Composites. J. Am. Ceram. Soc. 2016, 99, 281–285. [Google Scholar] [CrossRef]
- Qiu, L.; Li, Y.M.; Zheng, X.H.; Zhu, J.; Tang, D.W.; Wu, J.Q.; Xu, C.H. Thermal-Conductivity Studies of Macro-porous Polymer-Derived SiOC Ceramics. Int. J. Thermophys. 2014, 35, 76–89. [Google Scholar] [CrossRef]
- Radovanovic, E.; Gozzi, M.F.; Goncalves, M.C.; Yoshida, I.V.P. Silicon oxycarbide glasses from silicone networks. J. Non-Cryst. Solids 1999, 248, 37–48. [Google Scholar] [CrossRef]
- Thibault, N.W. Morphological and structural crystallography and optical properties of SiC. Am. Mineral. 1944, 29, 249–278. [Google Scholar]
- Papendorf, B.; Ionescu, E.; Kleebe, H.-J.; Linck, C.; Guillon, O.; Nonnenmacher, K.; Riedel, R. High-temperature creep behavior of dense SiOC-based ceramic nanocomposites: Microstructural and phase composition effects. J. Am. Ceram. Soc. 2013, 96, 272–280. [Google Scholar] [CrossRef]
- Ionescu, E.; Balan, C.; Kleebe, H.-J.; Mueller, M.M.; Guillon, O.; Schliephake, D.; Heilmaier, M.; Riedel, R. High-temperature creep behavior of SiOC glass-ceramics: Influence of network carbon versus segregated carbon. J. Am. Ceram. Soc. 2014, 97, 3935–3942. [Google Scholar] [CrossRef]
- Ferrari, A.C.; Robertson, J. Interpretation of Raman spectra of disordered and amorphous carbon. Phys. Rev. B 2000, 61, 14095–14107. [Google Scholar] [CrossRef]
- Cancado, L.G.; Takai, K.; Enoki, T.; Endo, M.; Kim, Y.A.; Mizusaki, H.; Jorio, A.; Coelho, L.N.; Magalhães-Paniago, R.; Pimenta, M.A. General equation for the determination of the crystallite size La of nanographite by Raman spectroscopy. Appl. Phys. Lett. 2006, 88, 163106. [Google Scholar] [CrossRef]
- Cancado, L.G.; Jorio, A.; Ferreira, E.H.M.; Stavale, F.; Achete, C.A.; Capaz, R.B.; Moutinho, M.V.O.; Lombardo, A.; Kulmala, T.S.; Ferrari, A.C. Quantifying Defects in Graphene via Raman Spectroscopy at Different Excitation Energies. Nano Lett. 2011, 11, 3190–3196. [Google Scholar] [CrossRef] [PubMed]
- Larouche, N.; Stansfield, B.L. Classifying nanostructured carbons using graphitic indices derived from Raman spectra. Carbon 2010, 48, 620–629. [Google Scholar] [CrossRef]
- Roth, F.; Waleska, P.; Hess, C.; Ionescu, E.; Nicoloso, N. UV Raman spectroscopy of segregated carbon in silicon oxycarbides. J. Ceram. Soc. Jpn. 2016, 124, 1042–1045. [Google Scholar] [CrossRef]
- Cuesta, A.; Dhamelincourt, P.; Laureyns, J.; Martinez-Alonso, A.; Tascon, J.M.D. Raman microprobe studies on carbon materials. Carbon 1994, 32, 1523–1532. [Google Scholar] [CrossRef]
- Smith, D.S.; Alzina, A.; Bourret, J.; Nait-Ali, B.; Pennec, F.; Tessier-Doyen, N.; Otsu, K.; Matsubara, H.; Elser, P.; Gonzenbach, U.T. Thermal conductivity of porous materials. J. Mater. Res. 2013, 28, 2260–2272. [Google Scholar] [CrossRef]
- Piat, R.; Schnack, E. Identification of coefficients of thermal expansion of pyrolytic carbon with different texture degrees. Key Eng. Mater. 2003, 251–252, 333–338. [Google Scholar] [CrossRef]
- Li, Z.; Bradt, R.C. Thermal expansion of the cubic (3C) polytype of silicon carbide. J. Mater. Sci. 1986, 21, 4366–4368. [Google Scholar] [CrossRef]
- Debenedetti, P.G.; Truskett, T.M.; Lewis, C.P.; Stillinger, F.H. Theory of supercooled liquids and glasses: Energy landscape and statistical geometry perspectives. In Advances in Chemical Engineering; Academic Press: Cambridge, MA, USA, 2001; pp. 21–79. [Google Scholar]
- Mattern, N.; Hermann, H.; Roth, S.; Sakowski, J.; Macht, M.-P.; Jovari, P.; Jiang, J. Structural behavior of Pd40Cu30Ni10P20 bulk metallic glass below and above the glass transition. Appl. Phys. Lett. 2003, 82, 2589–2591. [Google Scholar] [CrossRef] [Green Version]
- Doremus, R.H. Viscosity of silica. J. Appl. Phys. 2002, 92, 7619–7629. [Google Scholar] [CrossRef]
- Mazurin, O.V. Problems of compatibility of the values of glass transition temperatures published in the world literature. Glass Phys. Chem. 2007, 33, 22–36. [Google Scholar] [CrossRef]
- Stabler, C.; Roth, F.; Narisawa, M.; Schliephake, D.; Heilmaier, M.; Lauterbach, S.; Kleebe, H.-J.; Riedel, R.; Lonescu, E. High-temperature creep behavior of a SiOC glass ceramic free of segregated carbon. J. Eur. Ceram. Soc. 2016, 36, 3747–3753. [Google Scholar] [CrossRef]
- MacLeod, I.A. Modern Structural Analysis: Modelling Process and Guidance; Thomas Telford Ltd.: London, UK, 2005. [Google Scholar]
- Sosman, R.B. The Properties of Silica: An Introduction to the Properties of Substances in the Solid Non-Conducting State; The Chemical Catalog Company, Inc.: New York, NY, USA, 1927. [Google Scholar]
- Chase, M.W.J. NIST-JANAF Thermochemical Tables; American Institute of Physics: College Park, MA, USA, 1998. [Google Scholar]
- Yokoyama, J.; Murabayashi, M.; Takahashi, Y.; Mukaibo, T. Measurement of high-temperature thermal properties of glassy carbon by laser flash method. Tanso 1971, 65, 44–47. [Google Scholar] [CrossRef]
- Kanamori, H.; Fujii, N.; Mizutani, H. Thermal diffusivity measurement of rock-forming minerals from 300° to 1100° K. J. Geophys. Res. 1968, 73, 595–605. [Google Scholar] [CrossRef]
- Kim, K.J.; Lim, K.-Y.; Kim, Y.-W. Electrical and Thermal Properties of SiC Ceramics Sintered with Yttria and Nitrides. J. Am. Ceram. Soc. 2014, 97, 2943–2949. [Google Scholar] [CrossRef]
- Posselt, D.; Kjems, J.K.; Bernasconi, A.; Sleator, T.; Ott, H.R. The Thermal-Conductivity of Silica Aerogel in the Phonon, the Fracton and the Particle-Mode Regime. Europhys. Lett. 1991, 16, 59–65. [Google Scholar] [CrossRef]
- Nakayama, T. Boson peak and terahertz frequency dynamics of vitreous silica. Rep. Prog. Phys. 2002, 65, 1195–1242. [Google Scholar] [CrossRef]
- Alexander, S.; Laermans, C.; Orbach, R.; Rosenberg, H.M. Fracton interpretation of vibrational properties of cross-linked polymers, glasses, and irradiated quartz. Phys. Rev. B 1983, 28, 4615–4619. [Google Scholar] [CrossRef]
- Loeb, A.L. Thermal conductivity. VIII. A theory of thermal conductivity of porous materials. J. Am. Ceram. Soc. 1954, 37, 96–99. [Google Scholar] [CrossRef]
- Eucken, A. The heat conductivities of ceramic refractory materials. Calculations of heat conductivity from the constituents. Forsch. Geb. Ingenieurwesen 1932, 16, 353–360. [Google Scholar]
- Cahill, D.G. Thermal Conductivity Data. 2014. Available online: http://users.mrl.illinois.edu/cahill/tcdata/tcdata.html (accessed on 14 December 2017).
- Ho, C.Y.; Powell, R.W.; Liley, P.E. Thermal conductivity of the elements. J. Phys. Chem. Ref. Data 1972, 1, 279–421. [Google Scholar] [CrossRef]
- Maxwell, J. A Treatise on Electricity and Magnetism; Clarendon Press: Oxford, UK, 1892. [Google Scholar]
- Garnett, J.C.M. Colours in metal glasses and in metallic films. Philos. Trans. R. Soc. Lond. Ser. A 1904, 203, 385–420. [Google Scholar] [CrossRef]
- Kingery, W.D. Thermal conductivity. XIV. Conductivity of multicomponent systems. J. Am. Ceram. Soc. 1959, 42, 617–627. [Google Scholar] [CrossRef]
- German, R.M. A model for the thermal properties of liquid-phase sintered composites. Metall. Trans. A 1993, 24, 1745–1752. [Google Scholar] [CrossRef]
- Wang, J.; Carson, J.K.; North, M.F.; Cleland, D.J. A new structural model of effective thermal conductivity for heterogeneous materials with co-continuous phases. Int. J. Heat Mass Transf. 2008, 51, 2389–2397. [Google Scholar] [CrossRef]
- Jeong, T.; Zhu, J.-G.; Mao, S.; Pan, T.; Tang, Y.J. Thermal Characterization of SiC Amorphous Thin Films. Int. J. Thermophys. 2012, 33, 1000–1012. [Google Scholar] [CrossRef]
- Li, M.; Yue, Y. Molecular dynamics study of thermal transport in amorphous silicon carbide thin film. RSC Adv. 2014, 4, 23010–23016. [Google Scholar] [CrossRef]








| Sample | Composition | SiO2 (mol %) | SiC (mol %) | Cfree (mol %) | SiO2 (vol %) | SiC (vol %) | Cfree (vol %) |
|---|---|---|---|---|---|---|---|
| C1–SiOC–1100 | SiO1.38C0.32 | 68.1 1 ± 1.1 | 30.7 1 ± 2.3 | 1.2 1 ± 2.9 | - | - | - |
| C1–SiOC–1600 | SiO1.41C0.30 | 70.2 ± 0.5 | 29.3 ± 2.1 | 0.5 ± 2.7 | 83.1 ± 0.4 | 16.8 ± 1.2 | 0.1 ± 0.7 |
| C12–SiOC–1600 | SiO1.50C0.71 | 51.3 ± 0.3 | 17.2 ± 1.4 | 31.5 ± 1.7 | 75.7 ± 0.4 | 12.3 ± 1.0 | 11.9 ± 0.7 |
| C16–SiOC–1600 | SiO1.27C0.97 | 39.6 ± 1.1 | 22.8 ± 1.7 | 37.6 ± 1.7 | 65.7 ± 1.9 | 18.3 ± 1.3 | 16.0 ± 0.7 |
| C17–SiOC–1600 | SiO0.94C1.13 | 29.5 ± 0.5 | 33.1 ± 1.4 | 37.4 ± 1.5 | 53.5 ± 0.9 | 29.1 ± 1.2 | 17.4 ± 0.7 |
| Sample | Csegregated (vol %) | AD/AG | La (nm) | Ld (nm) | Leq (nm) |
|---|---|---|---|---|---|
| C1–SiOC–1600 | 0.1 ± 0.7 | 4.868 ± 1.074 | 7.9 ± 1.7 | 7.7 ± 0.8 | 10.0 ± 0.5 |
| C12–SiOC–1600 | 11.9 ± 0.8 | 4.215 ± 0.251 | 9.2 ± 0.6 | 8.3 ± 0.3 | 11.0 ± 0.7 |
| C16–SiOC–1600 | 16.0 ± 0.7 | 4.121 ± 0.521 | 9.5 ± 1.3 | 8.4 ± 0.6 | 11.6 ± 3.3 |
| C17–SiOC–1600 | 17.4 ± 0.7 | 4.998 ± 0.340 | 7.5 ± 0.5 | 7.5 ± 0.2 | 10.1 ± 0.6 |
| Sample | Composition | Skeletal Density (g/cm3) | Open Porosity (vol %) | Closed Porosity (vol %) |
|---|---|---|---|---|
| Vitreous Silica | SiO2 | 2.20 | - | - |
| C1–SiOC–1100 | SiO1.38C0.32 | 2.28 | 0.3 | - |
| C1–SiOC–1600 | SiO1.41C0.30 | 2.38 | 0 | - |
| C12–SiOC–1600 | SiO1.50C0.71 | 2.31 | 0 | - |
| C16–SiOC–1600 | SiO1.27C0.97 | 2.34 | 0 | - |
| C17–SiOC–1600 | SiO0.94C1.13 | 2.33 | 1.6 | 7.0 |
| Sample | Composition | CTE (10−6 K−1) | CTEHT (10−6 K−1) |
|---|---|---|---|
| C1–SiOC–1100 | SiO1.38C0.32 | 3.23 | - |
| C1–SiOC–1600 | SiO1.41C0.30 | 1.84 | 4.41 |
| C12–SiOC–1600 | SiO1.50C0.71 | 2.02 | 4.87 |
| C16–SiOC–1600 | SiO1.27C0.97 | 3.09 | 5.29 |
| C17–SiOC–1600 | SiO0.94C1.13 | 3.23 | - |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stabler, C.; Reitz, A.; Stein, P.; Albert, B.; Riedel, R.; Ionescu, E. Thermal Properties of SiOC Glasses and Glass Ceramics at Elevated Temperatures. Materials 2018, 11, 279. https://doi.org/10.3390/ma11020279
Stabler C, Reitz A, Stein P, Albert B, Riedel R, Ionescu E. Thermal Properties of SiOC Glasses and Glass Ceramics at Elevated Temperatures. Materials. 2018; 11(2):279. https://doi.org/10.3390/ma11020279
Chicago/Turabian StyleStabler, Christina, Andreas Reitz, Peter Stein, Barbara Albert, Ralf Riedel, and Emanuel Ionescu. 2018. "Thermal Properties of SiOC Glasses and Glass Ceramics at Elevated Temperatures" Materials 11, no. 2: 279. https://doi.org/10.3390/ma11020279
APA StyleStabler, C., Reitz, A., Stein, P., Albert, B., Riedel, R., & Ionescu, E. (2018). Thermal Properties of SiOC Glasses and Glass Ceramics at Elevated Temperatures. Materials, 11(2), 279. https://doi.org/10.3390/ma11020279