1. Introduction
Many attempts have been made in the past few decades to obtain a deep understanding of and create a model of the metal cutting process by using analytical, experimental, mechanistic, and finite element methods [
1]. Remarkable work has been made by Merchant [
2] to determine the shear angle using an analytical model. Lee and Shaffer [
3] and Oxley and Hatton [
4] proposed analytical models for predicting the shear angle based on an assumption of a thick shear zone.
On the basis of shear plane theory, Das and Tobias [
5] developed a mathematical model describing the connection between static and dynamic cutting force coefficients with experimental methods. Wu [
6] proposed a new approach for obtaining dynamic cutting process parameters, using the time series based on dynamic data.
For an insight into the physical origins and dynamic phenomena, Lopez de Lacalle et al. [
7] developed a data acquisition system to simultaneously record the tool position and cutting forces for correlating machined surface geometry and cutting forces. By applying the mechanistic method, Armarego and Deshpande [
8], Kolartis and DeVries [
9], and Lazoglu and Liang [
10] established dynamic models of peripheral end milling and ball-end milling, respectively. In their models, the effect of system deflections on the chip load was taken into consideration.
Based on Armerego’s idea, Fernandez-Abia et al. [
11] took into consideration tool nose radius and proposed expressions for determining shearing and edge cutting coefficients for a wide range of cutting conditions. Lamikiz et al. [
12] presented a new method of obtaining the shear and ploughing specific cutting coefficients in ball-end milling. Wan et al. [
13] presented a unified, instantaneous cutting force model for flat end mills, using a transformation approach from orthogonal to oblique cutting process from Altintas [
14] and Armarego and Whitfield [
15].
The finite element method (FEM) is an effective approach in the study of cutting process modeling [
16]. Scippa et al. [
17] proposed a novel finite element approach (FEA) for the thin-wall milling process considering the effects of fixturing, tooltip dynamics, and material removal. This also showed that the finite element method could simulate the milling process. With the finite element method, Gonzalo et al. [
18,
19] proposed a new and inexpensive approach for obtaining cutting force coefficients using FEM models instead of cutting experiments.
The FEM has also been applied in the process modeling of Al-metal matrix composites (Al-MMCs), which have been one of the most important metal matrix composites, with low density, low cost, and increased strength and wear resistance [
20,
21]. To date, as a typical representative, the ex-situ SiC
p/Al MMCs have been widely and deeply researched [
22,
23] due to their relatively simple preparation process and low demand for equipment. During the cutting process, the chip morphology and segmentation was found to have a dominant influence on the material machinability [
24]. Hence, importance and significance has been attached to the analysis of chip formation in cutting process modeling for studying the mechanism of material machining deeply. Much research has been reported on the chip formation of ex-situ SiC
p/Al MMCs with experimental and finite element methods [
25,
26].
With turning tests on A359/SiC/20
p composite, Lin et al. [
27] found that tool wear had a great influence on the nature of the formed chip. In addition, it was concluded that the short chips were formed due to the reduction of material ductility, which resulted from the presence of ceramic particles.
Ge et al. [
28] found that chips of SiC
p/Al composite were formed non-uniformly and that the chip formation mechanisms, which were different from the adiabatic shear of titanic alloy, involved the micro-voids, micro-cracks, and strain concentration in the shear plane. Similarly, it was noted by Du et al. [
29] that the debonding failure of the particle-matrix interface, cracks and voids all played a vital role in the chip formation process.
Karthikeyan et al. [
30] studied the impact of particle volume fraction and cutting parameters on chip formation. It was found that the chip transformed from a continuous type to a discontinuous type with increasing particle volume fraction. With a decrease in feed or an increase in speed, continuous chip formation seemed to be easier due to the increased material ductility.
Huang et al. [
31] divided chips into three categories: Al-matrix, SiC particle, and Al–SiC mixed chips in grinding high-volume SiC
p/Al composites. It was found that the Al-matrix and SiC particle chips formed similarly due to plastic deformation and material brittleness. Reddy et al. [
32] also noted that hard particles in the matrix might decrease material ductility, which resulted in discontinuous, serrated, and saw-toothed chips. Joshi et al. [
33] found that the fracture initiated at the outer chip surface and propagated to the tool nose.
However, with only experimental tests and empirical methods as discussed above, it is difficult to penetrate the complex deformation process, such as elastic–plastic deformation, strain and stress, and temperature in the deformation zone and interactions, which could provide comprehensive and strong understanding. Hence, a large amount of deep research has also been carried out into understanding chip formation mechanisms during the cutting of SiCp/Al composites by applying sophisticated numerical techniques like the FEM.
Applying a 2D finite element (FE) model, Guo et al. [
34] conducted a study on the effect of cutting speed and tool rake angle on chip morphology in machining SiC
p/Al MMC. In their model, the material property was described with the Johnson–Cook (J–C) model. In addition, the arbitrary Lagrangian–Eulerian (ALE) method and the J–C damage model were both applied to define the chip separation criterion. The results showed that the rake angle and speed had a great impact on chip morphology. However, the formation process of the saw-toothed chip, which was commonly observed in the above experimental studies, was not presented.
Fathipour et al. [
35] built a 2D FE model and found that the chip separation usually performed along the particle–matrix interfaces. In addition, the chips were commonly saw-toothed, and the cutting parameters had a significant influence on the size and distance of the saw-tooth feature.
Wang et al. [
36] built multi-phase models of SiC
p/Al composites of different particle volume fractions. They believed that the debonding of the particle–matrix interfaces would take away part of the plastic deformation force, which would result in the decrease of cutting forces. From their simulation results, it was also found that chips of SiC
p/Al composites were segmented and would become more discontinuous as the particle volume fraction increased. Shui et al. [
37] developed three models with different particle types for simulating the cutting process of SiC
p/2024Al composites and found that chips of SiC
p/2024Al were mainly pieces or powder.
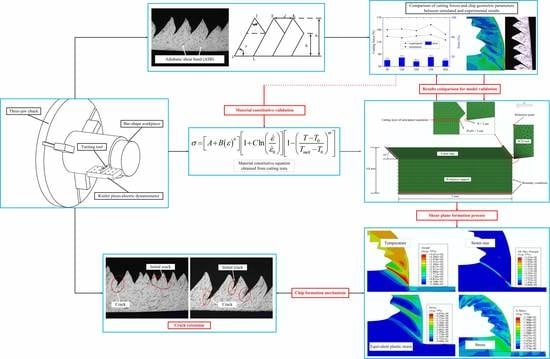
Up to now, a large number of papers have been published on ex-situ SiCp/Al MMCs. However, research on topics such as cutting performance, tool wear, machining modeling, or simulation on in-situ TiB2/7050Al MMC is rarely reported. In this study, the orthogonal cutting experiments and the FEM simulation methods were applied to investigate the chip formation mechanism of a new kind of in-situ TiB2/7050Al metal matrix composite. With experimental data, the influence of cutting parameters on chip geometric parameters was analyzed. In addition, the J–C constitutive equation was identified from the basic orthogonal cutting tests and validated with experiments and simulation tests. The stress, strain, temperature, and chip formation mechanisms around the material deformation zone were studied with the proposed FE simulation model.
3. Numerical Modeling
In this study, a two-dimensional FE model was built for chip formation simulation. As there is no constitutive equation for this new kind of in-situ 6 wt % TiB2/7050Al MMC, the J–C constitutive equation was applied to model its thermo-elastic-plastic behavior at present. Therefore, a set of orthogonal cutting experiments was conducted to obtain some material parameters needed for the J–C constitutive equation.
3.1. Definition of Material Constitutive Equation
The J–C constitutive equation used for modeling the thermo-elastic-plastic behavior of the in-situ TiB
2/7050Al MMC could be described as below:
where
σ is the flow stress and
ε,
,
means the effective plastic strain, the effective strain rate, and the reference strain rate (10
−3/s in this study), respectively.
T0 and
Tmelt stands for the room temperature and material melting temperature. The coefficients
A,
B,
C,
m, and
n stand for the yield strength, hardening modulus, strain rate sensitivity coefficient, thermal softening coefficient, and hardening coefficient, respectively.
In order to obtain the constants (
A,
B,
C,
m, and
n), the physical quantities on the shear plane (
σ,
ε,
, and
T) should be determined. From the research of Ref. [
41], the flow stress
σ, the effective plastic strain
ε, and the effective strain rate
could be determined on the basis of orthogonal cutting test results by the following formulas:
where
γ,
h, and
τshear stands for tool rake angle, primary shear zone thickness, and shear stress, respectively, which could be obtained from Merchant’s theory. In addition,
ρ is the mass density and
Cp is the specific heat.
With determined
σ,
ε,
, and
T, the five constants could be obtained using the least-square approximation (LSA) method. However, it was noticed in some studies [
42] that the least-square approximation method showed poor convergence and greatly depended on the searching point and boundary constraints. Hence, the genetic algorithm (GA) was applied to determine the constants by globally optimizing the following equation:
The material constitutive equation could be obtained after the aforementioned computation that was also presented with a flowchart in
Figure 4. As presented, the material constitutive constants (
A,
B,
C,
m, and
n) were output only when the chip morphology was similar and the relative error of the cutting force was less than 20%. After that, the obtained material constitutive parameters presented in
Table 6 were input into the simulation model. Then, the chip morphology and cutting forces of the FEM simulation and orthogonal cutting experiments were analyzed under the same cutting conditions for model validation.
3.2. Two-Dimensional Modeling
The commercial finite element simulation software Abaqus was applied in our research. In order to avoid the contact convergence and improve the physical comprehension of the chip formation, the Abaqus–Explicit approach was chosen for simulation analysis. As shown in
Figure 5, a two-dimensional coupled temperature-displacement analysis model was developed for the orthogonal cutting process simulation.
Because the hard PCD tool was used, whose elastic modulus was much larger than that of the workpiece, the tool was defined as an analytical rigid. The gradient grid method was used in meshing the cutting tool part, and the element density of the tool nose was much larger than that of other parts, as shown in
Figure 5. The total number of elements and nodes of the cutting tool was 599 and 338, respectively.
The workpiece model consisted of three parts: (a) the predefined uncut chip; (b) the cutting layer; and (c) the workpiece support. Due to the small volume (6 wt %) and nanometer size (50–200 nm), it was very difficult to create an uncut chip part with 6 wt % small particles and to define the interaction between the particles and the matrix material even by python programming. In addition, due to the huge size difference between the particle size (nanometer) and the uncut chip thickness (millimeter), the submitted simulation job was aborted easily due to mesh distortion, interaction relationship, and tremendous computing workload. Therefore, in our study, the uncut chip part was created as an isotropic monophasic part without particles.
The uncut chip thickness was set as 0.2 mm. In order to make sure the chip elements could climb up along the rake face successfully, the uncut chip part was modeled to a parallelogram with a trapezoidal head, as shown in
Figure 5. Linear quadrilateral continuum plane strain element with reduced integration (CPE4RT), distortion control, and hourglass control were used in meshing the predefined uncut chip part, and the mesh element was also a parallelogram with a length-to-height ratio of 8:10. The number of elements and nodes of the predefined uncut chip were 5120 and 5397, respectively.
In our simulation model, a cutting layer along the path of anticipated separation was used as the sacrificial layer. To avoid mesh distortion, the width of the cutting layer element should be larger than the cutting edge radius, and it was set as 5 μm in this study. For boundary conditions, the workpiece part was fixed on its bottom, left, and right sides, as well as the left side of the uncut chip part. The rigid tool part was designed to move from the right to the left at a range of cutting speeds (50 m/min–450 m/min) along the cutting layer.
3.3. Chip Separation Criterion and Chip–Tool Interface
It is very important to define the material failure criteria in the simulation of the material cutting process. According to the max stress, strain, and energy theory, there are many material failure criteria that could be used in the cutting process simulation, such as the J–C failure criterion, the shear damage, the ductile damage, and so on.
The J–C failure criterion is widely used in isotropic metal cutting simulations. Unfortunately, we could not obtain the J–C failure criterion for this new kind material from simple cutting tests. Even though it is possible to obtain the J–C failure criterion, it would cost months to perform a set of damage experiments with an expensive device. Hence, based on the shear damage, a chip separation criterion was developed using the shear failure module in our study:
where
εpl means the equivalent plastic strain,
means the damage plastic strain, and
D stands for the damage parameter. Only if the damage parameter equals 1 would the material fail and the mesh be deleted.
There are two contact zones in the simulation model between the cutting tool and the workpiece: (a) the contact between the rake face and the chip; (b) the contact between the rake face and the machined surface. Friction played an important role in the material cutting. The Coulomb friction law was applied to define the contact relationship as follow:
where
τc and
τth stand for the critical friction stress and the threshold value of the material failure, respectively. The parameter
p is the normal pressure across the contact interface, and
μ is the friction coefficient. As the PCD tool was very sharp and little serious adhesive wear phenomenon was found during the cutting experiments, the friction coefficient
μ was set as 0.1 in our simulation.