Insight on the Interplay between Synthesis Conditions and Thermoelectric Properties of α-MgAgSb
Abstract
:1. Introduction
2. Materials and Methods
3. Results
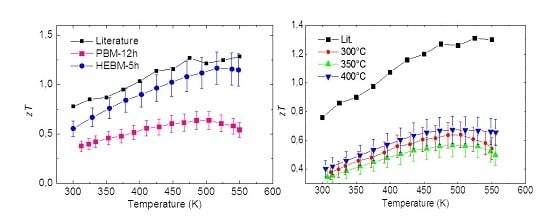
3.1. Comparison of High Energy Ball-Milling and Planetary Ball-Milling
3.2. Influence of Sintering Temperature with Planetary Ball-Milling
4. Discussion
4.1. Effect of Synthesis Route on Microstructure and Thermoelectric Properties
4.2. Effect of Impurity Phases on Thermoelectric Properties
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Karellas, S.; Leontaritis, A.D.; Panousis, G.; Bellos, E.; Kakaras, E. Energetic and exergetic analysis of waste heat recovery systems in the cement industry. Energy 2013, 58, 147–156. [Google Scholar] [CrossRef]
- Stabler, F. Automotive applications of high efficiency thermoelectrics. In Proceedings of the DARPA/ONR/DOE high efficiency thermoelectric workshop, San Diego, CA, USA, March 2002; pp. 1–26. [Google Scholar]
- Mazzetti, A.; Pret, M.G.; Pinarello, G.; Celotti, L.; Piskacev, M.; Cowley, A. Heat to electricity conversion systems for moon exploration scenarios: A review of space and ground technologies. Acta Astronaut. 2019, 156, 162–186. [Google Scholar] [CrossRef]
- Snyder, G.J.; Toberer, E.S. Complex thermoelectric materials. Nat. Mater. 2008, 7, 105. [Google Scholar] [CrossRef] [PubMed]
- Poudel, B.; Hao, Q.; Ma, Y.; Lan, Y.; Minnich, A.; Yu, B.; Yan, X.; Wang, D.; Muto, A.; Vashaee, D.; et al. High-Thermoelectric Performance of Nanostructured Bismuth Antimony Telluride Bulk Alloys. Science 2008, 320, 634–638. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rull-Bravo, M.; Moure, A.; Fernandez, J.F.; Martin-Gonzalez, M. Skutterudites as thermoelectric materials: Revisited. RSC Adv. 2015, 5, 41653–41667. [Google Scholar] [CrossRef]
- Puyet, M.; Dauscher, A.; Lenoir, B.; Dehmas, M.; Stiewe, C.; Mueller, E.; Hejtmanek, J. Beneficial effect of Ni substitution on the thermoelectric properties in partially filled Ca y Co 4− x Ni x Sb 12 skutterudites. J. Appl. Phys. 2005, 97, 083712. [Google Scholar] [CrossRef]
- Santos, R.; Yamini, S.A.; Dou, S.X. Recent progress in magnesium-based thermoelectric materials. J. Mater. Chem. A 2018, 6, 3328–3341. [Google Scholar] [CrossRef] [Green Version]
- Sankhla, A.; Patil, A.; Kamila, H.; Yasseri, M.; Farahi, N.; Mueller, E.; de Boor, J. Mechanical alloying of optimized Mg2 (Si, Sn) solid solutions: understanding phase evolution and tuning synthesis parameters for thermoelectric applications. ACS Appl. Energ. Mater. 2018, 1, 531–542. [Google Scholar] [CrossRef]
- Chen, S.; Ren, Z. Recent progress of half-Heusler for moderate temperature thermoelectric applications. Mater. Today 2013, 16, 387–395. [Google Scholar] [CrossRef]
- Sakurada, S.; Shutoh, N. Effect of Ti substitution on the thermoelectric properties of (Zr, Hf) NiSn half-Heusler compounds. Appl. Phys. Lett. 2005, 86, 082105. [Google Scholar] [CrossRef]
- Kirkham, M.J.; dos Santos, A.M.; Rawn, C.J.; Lara-Curzio, E.; Sharp, J.W.; Thompson, A.J. Ab initio determination of crystal structures of the thermoelectric material MgAgSb. Phys. Rev. B 2012, 85, 144120. [Google Scholar] [CrossRef]
- Zhao, H.; Sui, J.; Tang, Z.; Lan, Y.; Jie, Q.; Kraemer, D.; McEnaney, K.; Guloy, A.; Chen, G.; Ren, Z. High thermoelectric performance of MgAgSb-based materials. Nano Energy 2014, 7, 97–103. [Google Scholar] [CrossRef]
- Liu, Z.; Shuai, J.; Mao, J.; Wang, Y.; Wang, Z.; Cai, W.; Sui, J.; Ren, Z. Effects of antimony content in MgAg 0.97 Sb x on output power and energy conversion efficiency. Acta Mater. 2016, 102, 17–23. [Google Scholar] [CrossRef]
- Liu, Z.; Wang, Y.; Mao, J.; Geng, H.; Shuai, J.; Wang, Y.; He, R.; Cai, W.; Sui, J.; Ren, Z. Lithium doping to enhance thermoelectric performance of MgAgSb with weak electron–phonon coupling. Adv. Energy Mater. 2016, 6, 1502269. [Google Scholar] [CrossRef]
- Liu, Z.; Zhang, Y.; Mao, J.; Gao, W.; Wang, Y.; Shuai, J.; Cai, W.; Sui, J.; Ren, Z. The microscopic origin of low thermal conductivity for enhanced thermoelectric performance of Yb doped MgAgSb. Acta Mater. 2017, 128, 227–234. [Google Scholar] [CrossRef] [Green Version]
- Shuai, J.; Kim, H.S.; Lan, Y.; Chen, S.; Liu, Y.; Zhao, H.; Sui, J.; Ren, Z. Study on thermoelectric performance by Na doping in nanostructured Mg 1-x Na x Ag 0.97 Sb 0.99. Nano Energy 2015, 11, 640–646. [Google Scholar] [CrossRef]
- Sui, J.; Shuai, J.; Lan, Y.; Liu, Y.; He, R.; Wang, D.; Jie, Q.; Ren, Z. Effect of Cu concentration on thermoelectric properties of nanostructured p-type MgAg 0.97− xCuxSb 0.99. Acta Mater. 2015, 87, 266–272. [Google Scholar] [CrossRef]
- Tan, X.; Wang, L.; Shao, H.; Yue, S.; Xu, J.; Liu, G.; Jiang, H.; Jiang, J. Improving Thermoelectric Performance of α-MgAgSb by Theoretical Band Engineering Design. Adv. Energy Mater. 2017, 7, 1700076. [Google Scholar] [CrossRef]
- Lei, J.; Zhang, D.; Guan, W.; Ma, Z.; Cheng, Z.; Wang, C.; Wang, Y. Enhancement of thermoelectric figure of merit by the insertion of multi-walled carbon nanotubes in α-MgAgSb. Appl. Phys. Lett. 2018, 113, 083901. [Google Scholar] [CrossRef]
- Ying, P.; Liu, X.; Fu, C.; Yue, X.; Xie, H.; Zhao, X.; Zhang, W.; Zhu, T. High performance α-MgAgSb thermoelectric materials for low temperature power generation. Chem. Mater. 2015, 27, 909–913. [Google Scholar] [CrossRef]
- Liu, Z.; Geng, H.; Mao, J.; Shuai, J.; He, R.; Wang, C.; Cai, W.; Sui, J.; Ren, Z. Understanding and manipulating the intrinsic point defect in α-MgAgSb for higher thermoelectric performance. J. Mater. Chem. A 2016, 4, 16834–16840. [Google Scholar] [CrossRef]
- Li, D.; Zhao, H.; Li, S.; Wei, B.; Shuai, J.; Shi, C.; Xi, X.; Sun, P.; Meng, S.; Gu, L.; et al. Atomic Disorders Induced by Silver and Magnesium Ion Migrations Favor High Thermoelectric Performance in α-MgAgSb-Based Materials. Adv. Funct. Mater. 2015, 25, 6478–6488. [Google Scholar] [CrossRef]
- Lei, J.; Zhang, D.; Guan, W.; Cheng, Z.; Wang, C.; Wang, Y. Engineering Electrical Transport in a-MgAgSb to Realize High Performances near Room Temperature. Phys. Chem. Chem. Phys. 2018, 20, 16729–16735. [Google Scholar] [CrossRef] [PubMed]
- Zheng, Y.; Liu, C.; Miao, L.; Lin, H.; Gao, J.; Wang, X.; Chen, J.; Wu, S.; Li, X.; Cai, H. Cost effective synthesis of p-type Zn-doped MgAgSb by planetary ball-milling with enhanced thermoelectric properties. RSC Adv. 2018, 8, 35353–35359. [Google Scholar] [CrossRef] [Green Version]
- Tullberg, E.; Peters, D.; Frejd, T. The Heck reaction under ball-milling conditions. J. Organomet. Chem. 2004, 689, 3778–3781. [Google Scholar] [CrossRef]
- Schmitz, A.; Schmid, C.; Stiewe, C.; de Boor, J.; Mueller, E. Annealing and sintering effects in thermoelectric skutterudites synthesized by gas atomization. Phys. Status Solidi A. 2016, 213, 758–765. [Google Scholar] [CrossRef]
- Stiewe, C.; Sottong, R.; de Boor, J.; Mueller, E. Upscaled Synthesis of n-and p-Type Thermoelectric Skutterudite Single Legs by Gas Atomization and Current-Assisted Sintering. Phys. Status Solidi A 2018, 215, 1700995. [Google Scholar] [CrossRef]
- De Boor, J.; Stiewe, C.; Ziolkowski, P.; Dasgupta, T.; Karpinski, G.; Lenz, E.; Edler, F.; Mueller, E. High-temperature measurement of Seebeck coefficient and electrical conductivity. J. Electron. Mater. 2013, 42, 1711–1718. [Google Scholar] [CrossRef]
- De Boor, J.; Müller, E. Data analysis for Seebeck coefficient measurements. Rev. Sci. Instrum. 2013, 84, 065102. [Google Scholar] [CrossRef] [Green Version]
- Landau, L.D.; Lifshitz, E.M. Course of Theoretical Physics; Elsevier: Oxford, UK, 2013. [Google Scholar]
- Kamila, H.; Sahu, P.; Sankhla, A.; Yasseri, M.; Pham, H.N.; Dasgupta, T.; Mueller, E.; de Boor, J. Analyzing transport properties of p-type Mg 2 Si–Mg 2 Sn solid solutions: optimization of thermoelectric performance and insight into the electronic band structure. J. Mater. Chem. A 2019, 7, 1045–1054. [Google Scholar] [CrossRef]
- Liu, Z.; Gao, W.; Meng, X.; Li, X.; Mao, J.; Wang, Y.; Shuai, J.; Cai, W.; Ren, Z.; Sui, J. Mechanical properties of nanostructured thermoelectric materials α-MgAgSb. Scripta Mater. 2017, 127, 72–75. [Google Scholar] [CrossRef]
- Martin, J. Apparatus for the high temperature measurement of the Seebeck coefficient in thermoelectric materials. Rev. Sci. Instrum. 2012, 83, 065101. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ziolkowski, P.; Stiewe, C.; de Boor, J.; Druschke, I.; Zabrocki, K.; Edler, F.; Haupt, S.; König, J.; Mueller, E. Iron disilicide as high-temperature reference material for traceable measurements of Seebeck coefficient between 300 K and 800 K. J. Electron. Mater. 2017, 46, 51–63. [Google Scholar] [CrossRef]
- Kim, H.S.; Gibbs, Z.M.; Tang, Y.; Wang, H.; Snyder, G.J. Characterization of Lorenz number with Seebeck coefficient measurement. APL Mater. 2015, 3, 041506. [Google Scholar] [CrossRef] [Green Version]
- Tukmakova, A.; Novotelnova, A.; Samusevich, K.; Usenko, A.; Moskovskikh, D.; Smirnov, A.; Mirofyanchenko, E.; Takagi, T.; Miki, T.; Khovaylo, V. Simulation of Field Assisted Sintering of Silicon Germanium Alloys. Materials 2019, 12, 570. [Google Scholar] [CrossRef]
- Frost, B.; Raynor, G.V. The system silver-magnesium-antimony, with reference to the theory of alloy formation. Proc. R. Soc. Lond. A 1950, 203, 132–147. [Google Scholar]
- Sheng, C.Y.; Liu, H.J.; Fan, D.D.; Cheng, L.; Zhang, J.; Wei, J.; Liang, J.H.; Jiang, P.H.; Shi, J. Predicting the optimized thermoelectric performance of MgAgSb. J. Appl. Phys. 2016, 119, 195101. [Google Scholar] [CrossRef] [Green Version]
- Bellanger, P.; Gorsse, S.; Bernard-Granger, G.; Navone, C.; Redjaimia, A.; Vivès, S. Effect of microstructure on the thermal conductivity of nanostructured Mg-2(Si,Sn) thermoelectric alloys: An experimental and modeling approach. Acta Mater. 2015, 95, 102–110. [Google Scholar] [CrossRef]
- Jain, A.; Ong, S.P.; Hautier, G.; Chen, W.; Richards, W.D.; Dacek, S.; Cholia, S.; Gunter, D.; Skinner, D.; Ceder, G.; et al. Commentary: The Materials Project: A materials genome approach to accelerating materials innovation. APL Mater. 2013, 1, 011002. [Google Scholar] [CrossRef] [Green Version]
- Mi, J.L.; Ying, P.J.; Sist, M.; Reardon, H.; Zhang, P.; Zhu, T.J.; Zhao, X.B.; Iversen, B.B. Elaborating the Crystal Structures of MgAgSb Thermoelectric Compound: Polymorphs and Atomic Disorders. Chem. Mater. 2017, 29, 6378–6388. [Google Scholar] [CrossRef] [Green Version]








| Milling Type | α-MgAgSb (wt.%) | Dyscrasite (Ag3Sb) (wt.%) | Sb (wt.%) | Mg3Sb2 (wt.%) | Ag3Mg (wt.%) | AgMg (wt.%) | GOF | Rwp |
|---|---|---|---|---|---|---|---|---|
| PBM | 60.9 | 2.2 | 16.8 | 5.7 | 0.6 | 13.7 | 5.54 | 9.41 |
| HEBM | 98.4 | 0 | 0 | 1.6 | 0 | 0 | 2.27 | 20.64 |
| Milling Type | Seebeck Coefficient (µV/K) | Electrical Conductivity (S/cm) | p (cm−3) | µ (cm2/Vs) |
|---|---|---|---|---|
| Liu et al. | 215 | 500 | 5.5 × 1019 | 55 |
| PBM | 114 | 860 | 3.3 × 1020 | 16 |
| HEBM | 259 | 178 | 4.5 × 1019 | 25 |
| Sintering Temperature (°C) | α-MgAgSb (wt.%) | Dyscrasite (Ag3Sb) (wt.%) | Sb (wt.%) | Mg3Sb2 (wt.%) | |
| 300 | 60.9 | 2.2 | 16.8 | 5.7 | |
| 350 | 89.9 | 0 | 8.8 | 0 | |
| 400 | 86.7 | 1.8 | 11.4 | 0 | |
| Sintering Temperature (°C) | Ag3Mg (wt.%) | AgMg (wt.%) | γ-MgAgSb (wt.%) | GOF | Rwp |
| 300 | 0.6 | 13.7 | 0 | 5.54 | 9.41 |
| 350 | 0 | 0 | 1.4 | 5.76 | 13.37 |
| 400 | 0 | 0 | 0.1 | 2.92 | 19.32 |
| Sintering Temperature (°C) | Seebeck Coefficient (µV/K) | Electrical Conductivity (S/cm) | p (cm−3) | µ (cm2/Vs) |
|---|---|---|---|---|
| Liu et al. (300 °C) | 215 | 500 | 5.5 × 1019 | 55 |
| 300 | 114 | 860 | 3.3 × 1020 | 16 |
| 350 | 153 | 762 | 1.8 × 1020 | 26 |
| 400 | 154 | 817 | 1.8 × 1020 | 28 |
| Ag3Sb (wt.%) | Seebeck (µV/K) | Electrical Conductivity (S/cm) | p (cm−3) | µ (cm2/Vs) |
|---|---|---|---|---|
| 0 (Liu et al.) | 215 | 500 | 5.50 × 1019 | 55 |
| 2.3 | 206 | 255 | 8.8 × 1019 | 18 |
| 5.5 | 172 | 574 | 1.4 × 1020 | 26 |
| γ-MgAgSb (wt.%) | Seebeck (µV/K) | Sigma (S/cm) | p (cm−3) | µ (cm2/Vs) |
|---|---|---|---|---|
| 0 (Liu et al.) | 215 | 500 | 5.5 × 1019 | 55 |
| 1.5 | 172 | 574 | 1.4 × 1020 | 26 |
| 4.6 | 202 | 320 | 9.3 × 1019 | 21 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Camut, J.; Barber Rodriguez, I.; Kamila, H.; Cowley, A.; Sottong, R.; Mueller, E.; de Boor, J. Insight on the Interplay between Synthesis Conditions and Thermoelectric Properties of α-MgAgSb. Materials 2019, 12, 1857. https://doi.org/10.3390/ma12111857
Camut J, Barber Rodriguez I, Kamila H, Cowley A, Sottong R, Mueller E, de Boor J. Insight on the Interplay between Synthesis Conditions and Thermoelectric Properties of α-MgAgSb. Materials. 2019; 12(11):1857. https://doi.org/10.3390/ma12111857
Chicago/Turabian StyleCamut, Julia, Ignacio Barber Rodriguez, Hasbuna Kamila, Aidan Cowley, Reinhard Sottong, Eckhard Mueller, and Johannes de Boor. 2019. "Insight on the Interplay between Synthesis Conditions and Thermoelectric Properties of α-MgAgSb" Materials 12, no. 11: 1857. https://doi.org/10.3390/ma12111857
APA StyleCamut, J., Barber Rodriguez, I., Kamila, H., Cowley, A., Sottong, R., Mueller, E., & de Boor, J. (2019). Insight on the Interplay between Synthesis Conditions and Thermoelectric Properties of α-MgAgSb. Materials, 12(11), 1857. https://doi.org/10.3390/ma12111857