Experimental Verification and Comparative Analysis of Equivalent Methods on Metal’s Fixed Joint Interface
Abstract
:1. Introduction
2. Materials and Methods
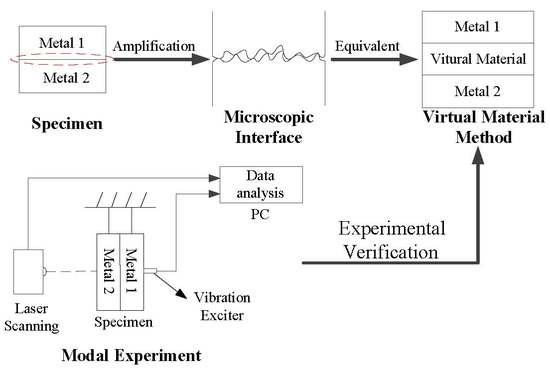
2.1. Virtual Material Method
2.2. Spring Damping Method and Finite Element Method
3. Simulation, Modal Experiment and Results
3.1. Modeling and Simulation
3.2. Modal Experiment
3.3. Results
4. Discussion
5. Conclusions
- The modal shapes of the modal experiment are roughly similar to the modal shapes obtained by the three equivalent methods of the joint interface. It is proved that all three methods can simulate the microscopic metal joint interface.
- The natural frequencies obtained by three equivalent methods of the metal joint interface have obvious deviations from the results of the modal experiment. The error of the natural frequency value obtained by the VMM is the smallest, being within 10%. Obviously, it is lower than the errors of the other two methods, which proves that the VMM is the closest to the real situation among the three equivalent methods of the metal joint interface.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Majumdar, A.; Tien, C.L. Fractal Characterization and Simulation of Rough Surfaces. Wear 1990, 136, 313–327. [Google Scholar] [CrossRef]
- Gagnepain, J.J.; Roques-Carmes, C. Fractal Approach to Two-Dimensional and Three-Dimensional Surface Roughness. Wear 1990, 109, 114–119. [Google Scholar] [CrossRef]
- Lopez, J.; Hansali, G.; Zahouani, H. 3D Fractal-Based Characterization for Engineered Surface Topography. Int. J. Mach. Tool Manuf. 1995, 35, 211–217. [Google Scholar] [CrossRef]
- Marotta, E.E.; Fletcher, L.S.; Dietz, T.A. Thermal Contact Resistance Modeling of Non-Flat, Roughened Surfaces with Non-Metallic Coatings. J. Heat Transf. 2000, 123, 11–23. [Google Scholar] [CrossRef]
- Majumdar, A.; Bhushan, B. Role of Fractal Geometry in Roughness Characterization and Contact Mechanics of Surfaces. J. Tribol. 1990, 112, 205–216. [Google Scholar] [CrossRef]
- Ibrahim, R.A.; Pettit, C.L. Uncertainties and dynamic problems of bolted joints and other fasteners. J. Sound Vib. 2005, 279, 857–936. [Google Scholar] [CrossRef]
- Li, X.; Liang, Y.; Guo, H.; Ju, X.; Wen, B. Study on equivalent model of generalized clearance of joint surface. J. Vib. Eng. 2014, 27, 25–32. [Google Scholar]
- Tian, H.; Li, B.; Liu, H.; Mao, K.; Peng, F.; Huang, X. A new method of virtual material hypothesis-based dynamic modeling on fixed joint interface in machine tools. Int. J. Mach. Tool Manuf. 2011, 51, 239–249. [Google Scholar] [CrossRef]
- Yuan, Y.; Gan, L.; Liu, K.; Yang, X. Elastoplastic Contact Mechanics Model of Rough Surface Based on Fractal Theory. Chin. J. Mech. Eng. 2017, 30, 207–215. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, C.; Cai, L.; Shi, W.; Liu, Z. Surface contact stress-based nonlinear virtual material method for dynamic analysis of bolted joint of machine tool. Precis. Eng. 2016, 43, 230–240. [Google Scholar] [CrossRef]
- Huang, K.; Jin, J. Research on Bolt Preload Simulation Based on Virtual Material Method. Mach. Des. Manuf. 2012, 8, 148–150. [Google Scholar]
- Jana, T.; Anirban, M.; Prasanta, S. Dynamic contact interactions of fractal surfaces. Appl. Surf. Sci. 2017, 392, 872–882. [Google Scholar] [CrossRef]
- Zhang, K.; Li, G.; Gong, J.; Zhang, M. Normal contact stiffness of rough surfaces considering oblique asperity contact. Adv. Mech. Eng. 2019, 11, 1–14. [Google Scholar] [CrossRef]
- Pan, W.; Li, X.; Wang, L.; Guo, N.; Mu, J. A normal contact stiffness fractal prediction model of dry-friction rough surface and experimental verification. Eur. J. Mech. A-Solid. 2017, 66, 94–102. [Google Scholar] [CrossRef]
- Mayer, M.H.; Gaul, L. Segment-to-segment contact elements for modelling joint interfaces in finite element analysis. Mech. Syst. Signal Process. 2007, 21, 724–734. [Google Scholar] [CrossRef]
- Ye, H.; Huang, Y.; Li, P.; Li, Y.; Bai, L. Virtual material parameter acquisition based on the basic characteristics of the bolt joint interfaces. Tribol. Int. 2016, 95, 109–117. [Google Scholar] [CrossRef]
- Yoshimura, M. Computer-aided design improvement of machine tool structure incorporating joint dynamics data. In Annals of the CIRP; CIRP: Paris, French, 1979; Volume 28, pp. 241–246. [Google Scholar]







| Methods | f1 (Hz) | f2 (Hz) | f3 (Hz) | f4 (Hz) | f5 (Hz) |
|---|---|---|---|---|---|
| VMM | 7140 | 1049.8 | 1228.8 | 1707.1 | 1790.1 |
| SDM | 855.8 | 1243.3 | 1540.6 | 2166.4 | 2237.8 |
| FEM | 867 | 1270.3 | 1504.2 | 2144.1 | 2211.7 |
| Order | ME | VMM | FEM | SDM |
|---|---|---|---|---|
| 1 |  |  |  |  |
| 2 |  |  |  |  |
| 3 |  |  |  |  |
| 4 |  |  |  |  |
| 5 |  |  |  |  |
| Order | 1 | 2 | 3 | 4 | 5 |
|---|---|---|---|---|---|
| Error of VMM | 8.12% | 7.32% | 7.26% | 9.14% | 9.93% |
| Error of FEM | 31.18% | 12.14% | 13.52% | 37.08% | 35.26% |
| Error of SDM | 29.49% | 9.75% | 16.27% | 38.51% | 36.86% |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Han, R.; Li, G.; Gong, J.; Zhang, M.; Zhang, K. Experimental Verification and Comparative Analysis of Equivalent Methods on Metal’s Fixed Joint Interface. Materials 2019, 12, 2381. https://doi.org/10.3390/ma12152381
Han R, Li G, Gong J, Zhang M, Zhang K. Experimental Verification and Comparative Analysis of Equivalent Methods on Metal’s Fixed Joint Interface. Materials. 2019; 12(15):2381. https://doi.org/10.3390/ma12152381
Chicago/Turabian StyleHan, Renxiu, Guoxi Li, Jingzhong Gong, Meng Zhang, and Kai Zhang. 2019. "Experimental Verification and Comparative Analysis of Equivalent Methods on Metal’s Fixed Joint Interface" Materials 12, no. 15: 2381. https://doi.org/10.3390/ma12152381
APA StyleHan, R., Li, G., Gong, J., Zhang, M., & Zhang, K. (2019). Experimental Verification and Comparative Analysis of Equivalent Methods on Metal’s Fixed Joint Interface. Materials, 12(15), 2381. https://doi.org/10.3390/ma12152381