Anisotropic Compressive Behavior of Metallic Foams under Extreme Temperature Conditions
Abstract
:1. Introduction
2. Materials and Methods
2.1. Materials and Sample Preparation
2.2. Experimental Tests Setup
3. Results and Discussions
4. Conclusions
- ▪
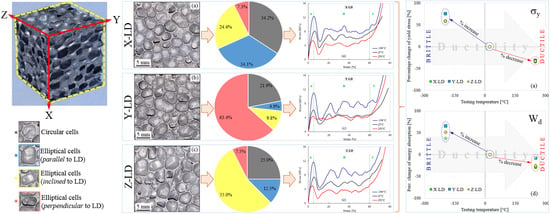
- Following the casting process, the AMF samples show a structural (geometrical) anisotropy with circular and elliptical cells of different sizes and orientations (Figure 1, Figure 6 and Figure 7). In addition, different intrinsic defects (intracellular cavities, micro-pores and thin cell walls) are found in the microstructure of the AMFs (Figure 6). These geometrical characteristics are essential for quantitatively rigorous predictions of main mechanical properties.
- ▪
- Regardless of the loading direction, the TT significantly influences the compression behavior of the AMFs. Due to the softening of the matrix, the mechanical properties significantly decrease with the increase of the testing temperature, and the collapse mechanism changes from a brittle one (−196 °C) to a ductile one (250 °C).
- ▪
- Regardless of the testing temperature, the mechanical property anisotropy is governed by the AMF’s microstructure. It was found that the elliptical cells, arranged in such a way that their large diameter are parallel to the direction of applying the compression load (abbreviated X-LD), can tolerate a higher stress compared to Y-LD and Z-LD (Table 1, Figure 4 and Figure 5).
- ▪
- Due to the brittle–ductile transition with the increase of the TT a decrease in stress amplitude (Δσ) is obtained. The highest Δσ is obtained for the X-LD, while the smallest one for the Y-LD.
- ▪
- The relative percentage change of normalized compressive properties significantly differs depending on the loading direction and testing temperature. For temperatures higher than RT, a percentage increase is obtained, while for temperatures lower than RT, a percentage decrease is obtained. The highest percentage increase (at −196 °C), and the smallest percentage reduction (at 250 °C) is obtained for Y-LD.
Author Contributions
Funding
Conflicts of Interest
References
- Liu, Y.F.; Wang, Y.Q. Size-Dependent Free Vibration and Buckling of Three-Dimensional Graphene Foam Microshells Based on Modified Couple Stress Theory. Materials 2019, 12, 729. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Rajak, D.K.; Mahajan, N.; Linul, E. Crashworthiness performance and microstructural characteristics of foam-filled thin-walled tubes under diverse strain rate. J. Alloy. Compd. 2019, 775, 675–689. [Google Scholar] [CrossRef]
- Novak, N.; Vesenjak, M.; Duarte, I.; Tanaka, S.; Hokamoto, K.; Krstulović-Opara, L.; Guo, B.; Chen, P.; Ren, Z. Compressive Behaviour of Closed-Cell Aluminium Foam at Different Strain Rates. Materials 2019, 12, 4108. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Kováik, J.; Jerz, J.; Mináriková, N.; Marsavina, L.; Linul, E. Scaling of compression strength in disordered solids: Metallic foams. Frattura ed Integrità Strutturale 2016, 10, 55–62. [Google Scholar] [CrossRef] [Green Version]
- Katona, B.; Szebényi, G.; Orbulov, I.N. Fatigue properties of ceramic hollow sphere filled aluminium matrix syntactic foams. Mater. Sci. Eng. A 2017, 679, 350–357. [Google Scholar] [CrossRef] [Green Version]
- Qian, C.; Liang, C.; He, Z.; Ji, W. Effect of Layer Thickness in Layered Aluminum Matrix Syntactic Foam. Materials 2019, 12, 4172. [Google Scholar] [CrossRef] [Green Version]
- Szlancsik, A.; Katona, B.; Bobor, K.; Májlinger, K.; Orbulov, I.N. Compressive behaviour of aluminium matrix syntactic foams reinforced by iron hollow spheres. Mater. Des. 2015, 83, 230–237. [Google Scholar] [CrossRef] [Green Version]
- Kovacik, J.; Marsavina, L.; Linul, E. Poisson’s Ratio of Closed-Cell Aluminium Foams. Materials 2018, 11, 1904. [Google Scholar] [CrossRef] [Green Version]
- Kádár, C.; Máthis, K.; Orbulov, I.N.; Chmelík, F.; Wiener, C. Monitoring the failure mechanisms in metal matrix syntactic foams during compression by acoustic emission. Mater. Lett. 2016, 173, 31–34. [Google Scholar] [CrossRef] [Green Version]
- Park, K.-B.; Kim, H.-T.; Her, N.-Y.; Lee, J.-M. Variation of Mechanical Characteristics of Polyurethane Foam: Effect of Test Method. Materials 2019, 12, 2672. [Google Scholar] [CrossRef] [Green Version]
- Ashby, M.F.; Evans, A.; Fleck, N.A.; Gibson, L.J.; Hutchinson, J.W.; Wadley, H.N.G. Metal Foams a Design Guide; Butter worth Heinemann: Boston, MA, USA, 2000. [Google Scholar]
- Linul, E.; Marsavina, L. Prediction of fracture toughness for open cell polyurethane foams by finite element micromechanical analysis. Iran. Poly. J. 2011, 20, 736–746. [Google Scholar]
- Myers, K.; Katona, B.; Cortés, P.; Orbulov, I.N. Quasi-static and high strain rate response of aluminum matrix syntactic foams under compression. Compos. Part A Appl. Sci. Manuf. 2015, 79, 82–91. [Google Scholar] [CrossRef] [Green Version]
- Sharma, V.; Zivic, F.; Grujovic, N.; Babcsan, N.; Babcsan, J. Numerical Modeling and Experimental Behavior of Closed-Cell Aluminum Foam Fabricated by the Gas Blowing Method under Compressive Loading. Materials 2019, 12, 1582. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Linul, E.; Movahedi, N.; Marsavina, L. On the Lateral Compressive Behavior of Empty and Ex-Situ Aluminum Foam-Filled Tubes at High Temperature. Materials 2018, 11, 554. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Ramamurty, U.; Paul, A. Variability in mechanical properties of a metal foam. Acta Mater. 2004, 52, 869–876. [Google Scholar] [CrossRef]
- Zheng, Z.; Yu, J.; Li, J. Dynamic crushing of 2D cellular structures: A finite element study. Int. J. Impact Eng. 2005, 32, 650–664. [Google Scholar] [CrossRef]
- Manonukul, A.; Srikudvien, P.; Tange, M.; Puncreobutr, C. Geometry anisotropy and mechanical property isotropy in titanium foam fabricated by replica impregnation method. Mater. Sci. Eng. A 2016, 655, 388–395. [Google Scholar] [CrossRef]
- Sulong, M.A.; Taherishargh, M.; Belova, I.V.; Murch, G.E.; Fiedler, T. On the mechanical anisotropy of the compressive properties of aluminium perlite syntactic foam. Comput. Mater. Sci. 2015, 109, 258–265. [Google Scholar] [CrossRef]
- Nosko, M.; Simančik, F.; Florek, R. Reproducibility of aluminum foam properties: Effect of precursor distribution on the structural anisotropy and the collapse stress and its dispersion. Mater. Sci. Eng. A 2010, 527, 5900–5908. [Google Scholar] [CrossRef]
- Vesenjak, M.; Veyhl, C.; Fiedler, T. Analysis of anisotropy and strain rate sensitivity of open-cell metal foam. Mater. Sci. Eng. A 2012, 541, 105–109. [Google Scholar] [CrossRef]
- Mu, Y.; Yao, G.; Luo, H. Effect of cell shape anisotropy on the compressive behavior of closed-cell aluminum foams. Mater. Des. 2010, 31, 1567–1569. [Google Scholar] [CrossRef]
- Park, C.; Nutt, S. Anisotropy and strain localization in steel foam. Mater. Sci. Eng. A 2001, 299, 68–74. [Google Scholar] [CrossRef]
- Linul, E.; Marşavina, L.; Linul, P.-A.; Kovacik, J. Cryogenic and high temperature compressive properties of Metal Foam Matrix Composites. Compos. Struct. 2019, 209, 490–498. [Google Scholar] [CrossRef]
- Shahapurkar, K.; Garcia, C.D.; Doddamani, M.; Kumar, G.C.M.; Prabhakar, P. Compressive behavior of cenosphere/epoxy syntactic foams in arctic conditions. Compos. Part B: Eng. 2018, 135, 253–262. [Google Scholar] [CrossRef]
- Fiedler, T.; Al-Sahlani, K.; Linul, P.; Linul, E. Mechanical properties of A356 and ZA27 metallic syntactic foams at cryogenic temperature. J. Alloy. Compd. 2020, 813, 152181. [Google Scholar] [CrossRef]
- Linul, E.; Movahedi, N.; Marsavina, L. The temperature effect on the axial quasi-static compressive behavior of ex-situ aluminum foam-filled tubes. Compos. Struct. 2017, 180, 709–722. [Google Scholar] [CrossRef]
- Kovacik, J.; Orovčík, Ľ.; Jerz, J. High-temperature compression of closed cell aluminium foams. Met. Mater. 2016, 54, 429–440. [Google Scholar] [CrossRef] [Green Version]
- Movahedi, N.; Linul, E. Quasi-static compressive behavior of the ex-situ aluminum-alloy foam-filled tubes under elevated temperature conditions. Mater. Lett. 2017, 206, 182–184. [Google Scholar] [CrossRef]
- Taherishargh, M.; Linul, E.; Broxtermann, S.; Fiedler, T. The mechanical properties of expanded perlite-aluminium syntactic foam at elevated temperatures. J. Alloy. Compd. 2018, 737, 590–596. [Google Scholar] [CrossRef]
- Movahedi, N.; Linul, E.; Marsavina, L. The Temperature Effect on the Compressive Behavior of Closed-Cell Aluminum-Alloy Foams. J. Mater. Eng. Perform. 2017, 27, 99–108. [Google Scholar] [CrossRef]
- ISO13314 Mechanical Testing of Metals—Ductility Testing—Compression Test for Porous and Cellular Metals; ISO: Geneva, Switzerland, 2011.
- Linul, E.; Marsavina, L.; Kovacik, J.; Tomasz, S. Dynamic and quasi-static compression tests of closed-cell aluminium alloy foams. P. Romanian Acad. A 2017, 18, 361–369. [Google Scholar]
- Luong, D.; Lehmhus, D.; Gupta, N.; Weise, J.; Bayoumi, M. Structure and Compressive Properties of Invar-Cenosphere Syntactic Foams. Materials 2016, 9, 115. [Google Scholar] [CrossRef] [Green Version]
- Yu, Q.; Zhao, Y.; Dong, A.; Li, Y. Preparation and Properties of C/C Hollow Spheres and the Energy Absorption Capacity of the Corresponding Aluminum Syntactic Foams. Materials 2018, 11, 997. [Google Scholar] [CrossRef] [Green Version]
- Movahedi, N.; Linul, E. Mechanical properties of Light Expanded Clay Aggregated (LECA) filled tubes. Mater. Lett. 2018, 217, 194–197. [Google Scholar] [CrossRef]
- Movahedi, N.; Murch, G.E.; Belova, I.V.; Fiedler, T. Effect of Heat Treatment on the Compressive Behavior of Zinc Alloy ZA27 Syntactic Foam. Materials 2019, 12, 792. [Google Scholar] [CrossRef] [Green Version]
- Wan, X.; Zhu, K.; Xu, Y.; Han, B.; Jing, T. Early Compressive Deformation of Closed-Cell Aluminum Foam Based on a Three-Dimensional Realistic Structure. Materials 2019, 12, 1792. [Google Scholar] [CrossRef] [Green Version]
- Movahedi, N.; Taherishargh, M.; Belova, I.V.; Murch, G.E.; Fiedler, T. Mechanical and Microstructural Characterization of an AZ91–Activated Carbon Syntactic Foam. Materials 2018, 12, 3. [Google Scholar] [CrossRef] [Green Version]
- Szlancsik, A.; Katona, B.; Kemény, A.; Károly, D. On the Filler Materials of Metal Matrix Syntactic Foams. Materials 2019, 12, 2023. [Google Scholar] [CrossRef] [Green Version]
- Rajak, D.K.; Pagar, D.D.; Menezes, P.L.; Linul, E. Fiber-Reinforced Polymer Composites: Manufacturing, Properties, and Applications. Polym. 2019, 11, 1667. [Google Scholar] [CrossRef] [Green Version]
- Kádár, C.; Chmelík, F.; Ugi, D.; Máthis, K.; Knapek, M. Damage Characterization during Compression in a Perlite-Aluminum Syntactic Foam. Materials 2019, 12, 3342. [Google Scholar] [CrossRef] [Green Version]
- Linul, E.; Serban, D.A.; Voiconi, T.; Marsavina, L.; Sadowski, T. Energy - Absorption and Efficiency Diagrams of Rigid PUR Foams. Key Eng. Mater. 2014, 601, 246–249. [Google Scholar] [CrossRef]
- Zhang, B.; Hu, S.; Fan, Z. Anisotropic Compressive Behavior of Functionally Density Graded Aluminum Foam Prepared by Controlled Melt Foaming Process. Materials 2018, 11, 2470. [Google Scholar] [CrossRef] [Green Version]
- Movahedi, N.; Zadeh, A.H. Effect of plasma electrolytic oxidation treatment on corrosion behavior of closed-cell Al-A356 alloy foam. Mater. Lett. 2016, 164, 558–561. [Google Scholar] [CrossRef]
- Movahedi, N.; Mirbagheri, S.M.H.; Hoseini, S.R. Effect of foaming temperature on the mechanical properties of produced closed-cell A356Aluminum foams with melting method. Met. Mater. Int. 2014, 20, 757–763. [Google Scholar] [CrossRef]
- Movahedi, N.; Mirbagheri, S.M.H. Comparison of the Energy Absorption of Closed-Cell Aluminum Foam Produced by Various Foaming Agents. Strength Mater. 2016, 48, 444–449. [Google Scholar] [CrossRef]
- Fiedler, T.; Movahedi, N.; York, L.; Broxtermann, S. Functionally-Graded Metallic Syntactic Foams Produced via Particle Pre-Compaction. Metals 2020, 10, 314. [Google Scholar] [CrossRef] [Green Version]
- Linul, E.; Lell, D.; Movahedi, N.; Codrean, C.; Fiedler, T. Compressive properties of zinc syntactic foams at elevated temperatures. Compos. Part B Eng. 2019, 167, 122–134. [Google Scholar] [CrossRef]









| Loading Direction | TT [°C] | [MPa] | [%] | [MPa] | [MPa] | [MPa] | [MPa] | [%] |
|---|---|---|---|---|---|---|---|---|
| X-LD | −196 | 12.20 | 4.19 | 4.19 | 7.67 | 9.26 | 9.05 | 58.23 |
| 25 | 7.68 | 6.18 | 6.18 | 6.26 | 5.98 | 5.95 | 60.32 | |
| 250 | 5.07 | 3.21 | 3.21 | 3.88 | 4.32 | 3.55 | 65.42 | |
| Y-LD | −196 | 10.69 | 4.36 | 7.40 | 6.47 | 5.81 | 8.41 | 56.50 |
| 25 | 6.08 | 5.09 | 4.88 | 4.33 | 4.37 | 4.37 | 58.30 | |
| 250 | 4.18 | 3.61 | 3.63 | 3.35 | 4.23 | 3.92 | 62.85 | |
| Z-LD | −196 | 11.47 | 4.33 | 8.26 | 8.46 | 8.27 | 8.09 | 57.34 |
| 25 | 7.22 | 5.87 | 5.73 | 5.75 | 5.76 | 4.96 | 59.09 | |
| 250 | 4.82 | 3.63 | 4.40 | 3.51 | 3.72 | 4.71 | 61.77 |
| Loading Direction | TT [°C] | Energy Absorption at Different Strains [MJ/m3] | ||||||
|---|---|---|---|---|---|---|---|---|
| 10% | 20% | 30% | 40% | 50% | 60% | 70% | ||
| X-LD | −196 | 0.87 | 1.46 | 2.33 | 3.14 | 3.92 | 4.92 | 5.97 |
| 25 | 0.52 | 1.01 | 1.63 | 2.31 | 2.93 | 3.59 | 4.45 | |
| 250 | 0.36 | 0.70 | 1.13 | 1.55 | 1.99 | 2.54 | 3.37 | |
| Y-LD | −196 | 0.76 | 1.23 | 1.90 | 2.69 | 3.45 | 4.20 | 5.11 |
| 25 | 0.40 | 0.71 | 1.17 | 1.64 | 2.37 | 2.53 | 3.09 | |
| 250 | 0.33 | 0.65 | 1.08 | 1.49 | 1.92 | 2.34 | 3.02 | |
| Z-LD | −196 | 0.78 | 1.34 | 2.18 | 3.01 | 3.90 | 4.89 | 5.87 |
| 25 | 0.49 | 0.94 | 1.50 | 2.05 | 2.63 | 3.23 | 4.10 | |
| 250 | 0.35 | 0.68 | 1.10 | 1.51 | 1.95 | 2.41 | 3.15 | |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Khezrzadeh, O.; Mirzaee, O.; Emadoddin, E.; Linul, E. Anisotropic Compressive Behavior of Metallic Foams under Extreme Temperature Conditions. Materials 2020, 13, 2329. https://doi.org/10.3390/ma13102329
Khezrzadeh O, Mirzaee O, Emadoddin E, Linul E. Anisotropic Compressive Behavior of Metallic Foams under Extreme Temperature Conditions. Materials. 2020; 13(10):2329. https://doi.org/10.3390/ma13102329
Chicago/Turabian StyleKhezrzadeh, Omid, Omid Mirzaee, Esmaeil Emadoddin, and Emanoil Linul. 2020. "Anisotropic Compressive Behavior of Metallic Foams under Extreme Temperature Conditions" Materials 13, no. 10: 2329. https://doi.org/10.3390/ma13102329
APA StyleKhezrzadeh, O., Mirzaee, O., Emadoddin, E., & Linul, E. (2020). Anisotropic Compressive Behavior of Metallic Foams under Extreme Temperature Conditions. Materials, 13(10), 2329. https://doi.org/10.3390/ma13102329