Structural Instability-Enabled Mechanical Sensors Using Fiber Bragg Grating
Abstract
:1. Introduction
2. Design Principle and Paradigm
2.1. Design Principle of Powerless Mechanical Sensors Using Structural Instability
2.2. Paradigm of FBG in Detecting Structural Instability
3. Experiments and Numerical Simulations on the Structural Instability of Cylindrical Cells
3.1. Fabrication of FBG Cylindrical Cells
3.2. Experiments and Numerical Simulations
3.3. FBG Detection of the Structural Instability of the Cylindrical Cells
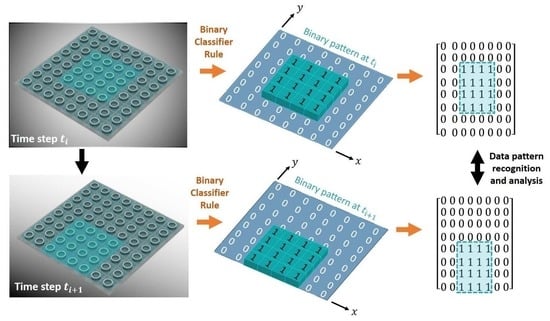
4. Pattern Recognition Analysis and Discussion on Potential Applications
4.1. Pattern Recognition Algorithm
4.2. Potential Applications of the Mechanical Sensors for Structural Health Monitoring (SHM)
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Jiao, P.; Borchani, W.; Alavi, A.H.; Hasni, H.; Lajnef, N. An energy harvesting and damage sensing solution based on postbuckling response of nonuniform cross-section beams. Struct. Control Health Monit. 2018, 25, e2052. [Google Scholar] [CrossRef]
- Soleimani, S.; Jiao, P.; Rajaei, S.; Forsati, R. A new approach for prediction of collapse settlement of sandy gravel soils. Eng. Comput. 2018, 34, 15–24. [Google Scholar] [CrossRef]
- Han, B.; Ou, J. Embedded piezoresistive cement-based stress/strain sensor. Sens. Actuators A-Phys. 2007, 138, 294–298. [Google Scholar] [CrossRef]
- Herrmann, J.; Mueller, K.H.; Reda, T.; Baxter, G.R.; Raguse, B.; de Groot, G.J.J.B.; Chai, R.; Roberts, M.; Wieczorek, L. Nanoparticle films as sensitive strain gauges. Appl. Phys. Lett. 2007, 91, 183105. [Google Scholar] [CrossRef]
- Carmo, J.P.; Ferreira da Silva, A.M.; Rocha, R.P.; Correia, J.H. Application of Fiber Bragg Gratings to Wearable Garments. IEEE Sens. J. 2012, 12, 261–266. [Google Scholar] [CrossRef]
- Xie, Y.; Geng, Z.; Zhuang, L.; Burla, M.; Taddei, C.; Hoekman, M.; Leinse, A.; Roeloffzen, C.G.H.; Boller, K.-J.; Lowery, A.J. Programmable optical processor chips: Toward photonic RF filters with DSP-level flexibility and MHz-band selectivity. Nanophotonics 2018, 7, 421–454. [Google Scholar] [CrossRef] [Green Version]
- Abro, Z.A.; Hong, C.; Chen, N.; Zhang, Y.; Lakho, R.A.; Yasin, S. A fiber Bragg grating-based smart wearable belt for monitoring knee joint postures. Text. Res. J. 2020, 90, 386–394. [Google Scholar] [CrossRef]
- Guo, Y.; Liu, W.; Xiong, L.; Kuang, Y.; Wu, H.; Liu, H. Fiber Bragg grating displacement sensor with high abrasion resistance for a steel spring floating slab damping track. Sensors 2018, 18, 1899. [Google Scholar] [CrossRef] [Green Version]
- Jinachandran, S.; Li, H.; Xi, J.; Prusty, B.G.; Semenova, Y.; Farrell, G.; Rajan, G. Fabrication and characterization of a magnetized metal-encapsulated FBG sensor for structural health monitoring. IEEE Sens. J. 2018, 18, 8739–8746. [Google Scholar] [CrossRef] [Green Version]
- Li, N.L.; Jiang, S.F.; Wu, M.H.; Shen, S.; Zhang, Y. Deformation monitoring for Chinese traditional timber buildings using fiber Bragg grating sensors. Sensors 2018, 18, 1968. [Google Scholar] [CrossRef] [Green Version]
- Wang, Y.; Yun, B.; Chen, N.; Cui, Y. Characterization of a high birefringence fibre Bragg grating sensor subjected to non-homogeneous transverse strain fields. Meas. Sci. Technol. 2006, 17, 939–942. [Google Scholar] [CrossRef]
- Urban, F.; Kadlec, J.; Vlach, R.; Kuchta, R. Design of a Pressure Sensor Based on Optical Fiber Bragg Grating Lateral Deformation. Sensors 2010, 10, 11212–11225. [Google Scholar] [CrossRef] [PubMed]
- Zhang, W.; Zhang, M.; Wang, X.; Zhao, Y.; Jin, B.; Dai, W. The analysis of FBG central wavelength variation with crack propagation based on a self-adaptive multi-peak detection algorithm. Sensors 2019, 19, 1056. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Viegas, D.; Abad, S.; Santos, J.L.; Ferreira, L.A.; Moita Araujo, F.M. Miniature High-Temperature Fiber Bragg Grating Sensor Design Based on U-Shaped Lossless Taper for Thermal Mapping Applications. IEEE Photonics Technol. Lett. 2010, 22, 811–813. [Google Scholar] [CrossRef]
- Laffont, G.; Cotillard, R.; Roussel, N.; Desmarchelier, R.; Rougeault, S. Temperature resistant fiber Bragg grating for on-line and structural health monitoring of the next-generation of nuclear reactors. Sensors 2018, 18, 1791. [Google Scholar] [CrossRef] [Green Version]
- Campopiano, S.; Cutolo, A.; Cusano, A.; Giordano, M.; Parente, G.; Lanza, G.; Laudati, A. Underwater Acoustic Sensors Based on Fiber Bragg Gratings. Sensors 2009, 9, 4446–4454. [Google Scholar] [CrossRef] [Green Version]
- De Lourenco, I., Jr.; Possetti, G.R.C.; Muller, M.; Fabris, J.L. Fiber Bragg Grating Sensor to Monitor Stress Kinetics in Drying Process of Commercial Latex Paints. Sensors 2010, 10, 4761–4776. [Google Scholar] [CrossRef]
- Wang, Y.; Wang, M.; Huang, X. High-sensitivity fiber Bragg grating transverse force sensor based on centroid measurement of polarization-dependent loss. Meas. Sci. Technol. 2010, 21, 065304. [Google Scholar] [CrossRef]
- Chen, C.; Zhang, X.Y.; Yu, Y.S.; Wei, W.H.; Guo, Q.; Qin, L.; Ning, Y.Q.; Wang, L.J.; Sun, H.B. Femtosecond laser-inscribed high-order Bragg grating in large-diameter sapphire fibers for high-temperature and strain sensing. J. Lightwave Technol. 2018, 36, 3302–3308. [Google Scholar] [CrossRef]
- Gasior, P.; Malesa, M.; Kaleta, J.; Kujawinska, M.; Malowany, K.; Rybczynski, R. Application of complementary optical methods for strain investigation in composite high pressure vessel. Compos. Struct. 2018, 203, 718–724. [Google Scholar] [CrossRef]
- Sohn, H.; Farrar, C.R.; Hunter, N.F.; Worden, K. Structural health monitoring using statistical pattern recognition techniques. J. Dyn. Syst. Meas. Control-Trans. Asme 2001, 123, 706–711. [Google Scholar] [CrossRef] [Green Version]
- Hill, K.O.; Meltz, G. Fiber Bragg grating technology fundamentals and overview. J. Lightwave Technol. 1997, 15, 1263–1276. [Google Scholar] [CrossRef] [Green Version]
- Kersey, A.D.; Davis, M.A.; Patrick, H.J.; LeBlanc, M.; Koo, K.P.; Askins, C.G.; Putnam, M.A.; Friebele, E.J. Fiber Grating Sensors. J. Lightwave Technol. 1997, 15, 1442–1463. [Google Scholar] [CrossRef] [Green Version]
- Othonos, A. Fiber Bragg gratings. Rev. Sci. Instrum. 1997, 68, 4309–4341. [Google Scholar] [CrossRef]
- Rao, Y.-J. In-fibre Bragg grating sensors. Meas. Sci. Technol. 1996, 8, 355–375. [Google Scholar] [CrossRef]
- Gafsi, R.; El-Sherif, M.A. Analysis of Induced-Birefringence Effects on Fiber Bragg Gratings. Opt. Fiber Technol. 2000, 6, 299–323. [Google Scholar] [CrossRef]
- Ren, N.; Yu, Y.; Jiang, X.; Li, Y. Improved multi-grating filtering demodulation method based on cascading neural networks for fiber Bragg grating sensor. J. Lightwave Technol. 2019, 37, 2147–2154. [Google Scholar] [CrossRef]
- MakerBot Replicator 2; MakerBot Industries: New York, NY, USA, 2009.
- Wu, S.; Yan, G.; Wang, C.; Lian, Z.; Chen, X.; He, S. FBG Incorporated Side-Open Fabry-Perot Cavity for Simultaneous Gas Pressure and Temperature Measurements. J. Lightwave Technol. 2016, 34, 3761–3767. [Google Scholar] [CrossRef]
- Chiavaioli, F.; Gouveia, C.A.J.; Jorge, P.A.S.; Baldini, F. Towards a Uniform Metrological Assessment of Grating-Based Optical Fiber Sensors: From Refractometers to Biosensors. Biosensors 2017, 7, 23. [Google Scholar] [CrossRef] [Green Version]
- Ottman, G.K.; Hofmann, H.F.; Lesieutre, G.A. Optimized piezoelectric energy harvesting circuit using step-down converter in discontinuous conduction mode. IEEE Trans. Power Electron. 2003, 18, 696–703. [Google Scholar] [CrossRef]
- Sundaram, B.A.; Ravisankar, K.; Senthil, R.; Parivallal, S. Wireless sensors for structural health monitoring and damage detection techniques. Curr. Sci. 2013, 104, 1496–1505. [Google Scholar]
- Salehi, H.; Chakrabartty, S.; Biswas, S.; Burgueno, R. Localized damage identification in plate-like structures using self-powered sensor data: A pattern recognition strategy. Measurement 2019, 135, 23–38. [Google Scholar] [CrossRef]




| Cylinders (Polylactic Acid PLA) | Fiber Bragg Grating (FBG) | ||
|---|---|---|---|
| Mater. | Density (g/cm3) | 1.24 | 2.20 |
| Young’s modulus (GPa) | 3.47 | 73.02 | |
| Elongation at break (%) | 5.2 | 2 | |
| Tensile modulus | 1.34 | -- | |
| Geo. | Length (mm) | 50, 60, 70 | 5 |
| Diameter (mm) | 30 | 0.125 | |
| Thickness (mm) | 0.4 | -- | |
| FE | Element type | S4R | -- |
| Element size (mm) | 3 | -- | |
| Load | Amplitude (mm) | 0.8 | |
| Time (s) | 100 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiao, P.; Xie, Y.; Wu, S.; Liu, X. Structural Instability-Enabled Mechanical Sensors Using Fiber Bragg Grating. Materials 2020, 13, 2599. https://doi.org/10.3390/ma13112599
Jiao P, Xie Y, Wu S, Liu X. Structural Instability-Enabled Mechanical Sensors Using Fiber Bragg Grating. Materials. 2020; 13(11):2599. https://doi.org/10.3390/ma13112599
Chicago/Turabian StyleJiao, Pengcheng, Yiwei Xie, Shengnan Wu, and Xinyu Liu. 2020. "Structural Instability-Enabled Mechanical Sensors Using Fiber Bragg Grating" Materials 13, no. 11: 2599. https://doi.org/10.3390/ma13112599
APA StyleJiao, P., Xie, Y., Wu, S., & Liu, X. (2020). Structural Instability-Enabled Mechanical Sensors Using Fiber Bragg Grating. Materials, 13(11), 2599. https://doi.org/10.3390/ma13112599