Role of the La/K Compositional Ratio in the Properties of Waveguides Written by Fs-Laser Induced Element Redistribution in Phosphate-Based Glasses
Abstract
:1. Introduction
2. Materials and Methods
2.1. Glass Samples Preparation, Composition, and Refractive Index Measurements
2.2. Fs-Laser Writing and Characterization of the Light Guiding Structures
3. Results and Discussion
3.1. Refractive Index and Molar Polarizabilities of the Samples
3.2. Morphology of the Structures, Guiding Performance and Refractive Index Contrast Estimations
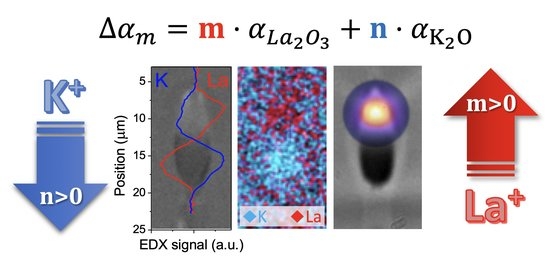
3.3. Compositional Characterization and Calculation of the Expected Index Contrast Based on Polarizabilities
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Osellame, R.; Della Valle, G.; Chiodo, N.; Taccheo, S.; Laporta, P.; Svelto, O.; Cerullo, G. Lasing in femtosecond laser written optical waveguides. Appl. Phys. A 2008, 93, 17–26. [Google Scholar] [CrossRef]
- Ródenas, A.; Gu, M.; Corrielli, G.; Paiè, P.; John, S.; Kar, A.K.; Osellame, R. Three-dimensional femtosecond laser nanolithography of crystals. Nat. Photonics 2019, 13, 105–109. [Google Scholar] [CrossRef]
- Osellame, R.; Cerullo, G.; Ramponi, R. Femtosecond Laser Micromachining, Topics in Applied Physics; Springer: Berlin, Germany, 2012; Volume 123. [Google Scholar]
- Fernandez, T.T.; Sakakura, M.; Eaton, S.M.; Sotillo, B.; Siegel, J.; Solis, J.; Shimotsuma, Y.; Miura, K. Bespoke photonic devices using ultrafast laser driven ion migration in glasses. Prog. Mater. Sci. 2018, 94, 68–113. [Google Scholar] [CrossRef]
- Liu, Y.; Shimizu, M.; Zhu, B.; Dai, Y.; Qian, B.; Qiu, J.; Shimotsuma, Y.; Miura, K.; Hirao, K. Micromodification of element distribution in glass using femtosecond laser irradiation. Opt. Lett. 2009, 34, 136–138. [Google Scholar] [CrossRef] [Green Version]
- Kanehira, S.; Miura, K.; Hirao, K. Ion exchange in glass using femtosecond laser irradiation. Appl. Phys. Lett. 2008, 93, 023112. [Google Scholar] [CrossRef] [Green Version]
- Toney Fernandez, T.; Haro-González, P.; Sotillo, B.; Hernandez, M.; Jaque, D.; Fernandez, P.; Domingo, C.; Siegel, J.; Solis, J. Ion migration assisted inscription of high refractive index contrast waveguides by femtosecond laser pulses in phosphate glass. Opt. Lett. 2013, 38, 5248–5251. [Google Scholar] [CrossRef] [Green Version]
- Del Hoyo, J.; Vazquez, R.M.; Sotillo, B.; Fernandez, T.T.; Siegel, J.; Fernández, P.; Osellame, R.; Solis, J. Control of waveguide properties by tuning femtosecond laser induced compositional changes. Appl. Phys. Lett. 2014, 105, 131101. [Google Scholar] [CrossRef] [Green Version]
- del Hoyo, J.; Moreno-Zarate, P.; Escalante, G.; Valles, J.A.; Fernandez, P.; Solis, J. High-Efficiency Waveguide Optical Amplifiers and Lasers via FS-Laser Induced Local Modification of the Glass Composition. J. Light. Technol. 2017, 35, 2955–2959. [Google Scholar] [CrossRef]
- Fletcher, L.B.; Witcher, J.J.; Reichman, W.B.; Arai, A.; Bovatsek, J.; Krol, D.M. Changes to the Network Structure of Er–Yb Doped Phosphate Glass Induced by Femtosecond Laser Pulses. J. Appl. Phys. 2009, 106, 083107. [Google Scholar] [CrossRef]
- Fletcher, L.B.; Witcher, J.J.; Troy, N.; Reis, S.T.; Brow, R.K.; Vazquez, R.M.; Osellame, R.; Krol, D.M. Femtosecond Laser Writing of Waveguides in Zinc Phosphate Glasses [Invited]. Opt. Mater. Express 2011, 1, 845–855. [Google Scholar] [CrossRef]
- Shimizu, M.; Miura, K.; Sakakura, M.; Nishi, M.; Shimotsuma, Y.; Kanehira, S.; Nakaya, T.; Hirao, K. Space-selective phase separation inside a glass by controlling compositional distribution with femtosecond-laser irradiation. Appl. Phys. A Mater. Sci. Process. 2010, 100, 1001–1005. [Google Scholar] [CrossRef]
- Sakakura, M.; Kurita, T.; Shimizu, M.; Yoshimura, K.; Shimotsuma, Y.; Fukuda, N.; Hirao, K.; Miura, K. Shape control of elemental distributions inside a glass by simultaneous femtosecond laser irradiation at multiple spots. Opt. Lett. 2013, 38, 4939–4942. [Google Scholar] [CrossRef] [PubMed]
- Rahman, M.A.; Saghir, M.Z. Thermodiffusion or Soret effect: Historical review. Int. J. Heat Mass Transf. 2014, 73, 693–705. [Google Scholar] [CrossRef]
- Köhler, W.; Morozov, K.I. The Soret Effect in Liquid Mixtures—A Review. J. Non Equilib. Thermodyn. 2016, 41, 151–197. [Google Scholar] [CrossRef]
- Fernandez, T.T.; Sotillo, B.; del Hoyo, J.; Valles, J.-A.; Vazquez, R.M.; Fernandez, P.; Solis, J. Dual Regimes of Ion Migration in High Repetition Rate Femtosecond Laser Inscribed Waveguides. IEEE Photonics Technol. Lett. 2015, 27, 1068–1071. [Google Scholar] [CrossRef] [Green Version]
- Dias, A.; Muñoz, F.; Alvarez, A.; Moreno-Zárate, P.; Atienzar, J.; Urbieta, A.; Fernandez, P.; Pardo, M.; Serna, R.; Solis, J. Femtosecond laser writing of photonic devices in borate glasses compositionally designed to be laser writable. Opt. Lett. 2018, 43, 2523–2526. [Google Scholar] [CrossRef]
- Brow, R.K.; Metwalli, E.; Sidebottom, D.L. Properties and structure of lanthanum phosphate glasses. Proc. SPIE 2000, 4102, 88–94. [Google Scholar]
- Karabulut, M.; Metwalli, E.; Brow, R. Structure and properties of lanthanum–aluminum–phosphate glasses. J. Non Cryst. Solids 2001, 283, 211–219. [Google Scholar] [CrossRef]
- Moreno-Zarate, P.; Gonzalez, A.; Funke, S.; Días, A.; Sotillo, B.; del Hoyo, J.; Garcia-Pardo, M.; Serna, R.; Fernandez, P.; Solis, J. Imaging Ellipsometry Determination of the Refractive Index Contrast and Dispersion of Channel Waveguides Inscribed by fs-Laser Induced Ion-Migration. Phys. Status Solidi 2018, 215, 1800258. [Google Scholar] [CrossRef]
- Duffy, J.A. The electronic polarisability of oxygen in glass and the effect of composition. J. Non Cryst. Solids 2002, 297, 275–284. [Google Scholar] [CrossRef]
- Jellison, G.E. Chapter 3, Data Analysis for Spectroscopic Ellipsometry. In Handbook of Ellipsometry; Tompkins, H.G., Irene, E.A., Eds.; William Andrew Publishing: Norwich, NY, USA, 2005; ISBN 9780815517474. [Google Scholar]
- Marcuse, D. Loss analysis of single-mode fiber splices. Bell Syst. Tech. J. 1977, 56, 703–718. [Google Scholar] [CrossRef]
- Hussey, C.D.; Martinez, F. Approximate analytical forms for the propagation characteristics of single-mode optical fibres. Electron. Lett. 1985, 21, 1103–1104. [Google Scholar] [CrossRef] [Green Version]
- Duffy, J.A. Electronic polarisability and related properties of the oxide ion. Phys. Chem. Glasses 1989, 30, 1–4. [Google Scholar]
- Dimitrov, V.; Komatsu, T. An Interpretation of Optical Properties of Oxides and Oxide Glasses in Terms of the Electronic Ion Polarizability and Average Single Bond Strength. J. Univ. Chem. Technol. Metall. 2010, 45, 219–250. [Google Scholar]
- Dimitrov, V.; Sakka, S. Electronic oxide polarizability and optical basicity of simple oxides. I. J. Appl. Phys. 1996, 79, 1736–1740. [Google Scholar] [CrossRef]
- Dimitrov, V.; Komatsu, T. Electronic Ion Polarizability, Optical Basicity and Metal (or Nonmetal) Binding Energy of Simple Oxides. J. Ceram. Soc. Jpn. 1999, 107, 879–886. [Google Scholar] [CrossRef] [Green Version]
- Honma, T.; Benino, Y.; Fujiwara, T.; Komatsu, T.; Sato, R.; Dimitrov, V. Electronic polarizability, optical basicity, and interaction parameter of La2O3 and related glasses. J. Appl. Phys. 2002, 91, 2942–2950. [Google Scholar] [CrossRef]
- Shannon, R.D. Dielectric polarizabilities of ions in oxides and fluorides. J. Appl. Phys. 1993, 73, 348–366. [Google Scholar] [CrossRef]
- Choi, J.H.; Shi, F.G.; Margaryan, A. Refractive index and low dispersion properties of new fluorophosphate glasses highly doped with rare-earth ions. J. Mater. Res. 2005, 20, 264–270. [Google Scholar] [CrossRef] [Green Version]
- Eaton, S.M.; Zhang, H.; Herman, P.R.; Yoshino, F.; Shah, L.; Bovatsek, J.; Arai, A. Heat accumulation effects in femtosecond laser-written waveguides with variable repetition rate. Opt. Express 2005, 13, 4708–4716. [Google Scholar] [CrossRef]
- Fernandez, T.T.; Siegel, J.; Hoyo, J.; Sotillo, B.; Fernandez, P.; Solis, J. Controlling plasma distributions as driving forces for ion migration during fs laser writing. J. Phys. D Appl. Phys. 2015, 48, 155101. [Google Scholar] [CrossRef] [Green Version]
- Del Hoyo, J.; de la Cruz, A.R.; Grace, E.; Ferrer, A.; Siegel, J.; Pasquazi, A.; Assanto, G.; Solis, J. Rapid assessment of nonlinear optical propagation effects in dielectrics. Sci. Rep. 2015, 5, 7650. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Reichman, W.J.; Krol, D.M.; Shah, L.; Yoshino, F.; Arai, A.; Eaton, S.M.; Herman, P.R. A spectroscopic comparison of femtosecond-laser-modified fused silica using kilohertz and megahertz laser systems. J. Appl. Phys. 2006, 99, 123112. [Google Scholar] [CrossRef]





| Sample | K2O | La2O3 | Al2O3 | SiO2 | P2O5 | Er2O3 | Yb2O3 | K2O/La2O3 | A | B |
|---|---|---|---|---|---|---|---|---|---|---|
| PS01 | 10.6 | 7.2 | 5.7 | 15.6 | 57.7 | 1 | 2.2 | 1.5 | 1.523 | 0.0006 |
| PS02 | 14.4 | 4.5 | 4.9 | 14.6 | 58.3 | 1 | 2.2 | 3.2 | 1.514 | 0.0056 |
| PS03 | 17.0 | 2.5 | 4.7 | 14.7 | 57.0 | 1.3 | 2.8 | 6.8 | 1.515 | 0.0069 |
| Polarizability (Å3) | K2O | La2O3 | Al2O3 | SiO2 | P2O5 |
|---|---|---|---|---|---|
| Total | 3.540 | 10.436 | 4.203 | 2.887 | 6.792 |
| 0.841 | 1.048 | 0.054 | 0.033 | 0.021 | |
| 1.858 | 2.780 | 1.365 | 1.427 | 1.350 (1.332) |
| Sample | La2O3 Enrichment (%) | K2O Depletion (%) | Estimated ∆n (×10−3) | Measured ∆n (×10−3) |
|---|---|---|---|---|
| PS01 | 25 ± 5 | 22 ± 5 | 11 ± 6 | 12.8 ± 2.0 |
| PS02 | 24 ± 7 | 9 ± 2 | 7.4 ± 5 | 6.6 ± 0.6 |
| PS03 | 29 ± 6 | 10 ± 4 | 1.6 ± 4 | 5.0 ± 0.4 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Moreno-Zarate, P.; Muñoz, F.; Sotillo, B.; Macias-Montero, M.; Atienzar, J.; Garcia-Pardo, M.; Fernandez, P.; Serna, R.; Solis, J. Role of the La/K Compositional Ratio in the Properties of Waveguides Written by Fs-Laser Induced Element Redistribution in Phosphate-Based Glasses. Materials 2020, 13, 1275. https://doi.org/10.3390/ma13061275
Moreno-Zarate P, Muñoz F, Sotillo B, Macias-Montero M, Atienzar J, Garcia-Pardo M, Fernandez P, Serna R, Solis J. Role of the La/K Compositional Ratio in the Properties of Waveguides Written by Fs-Laser Induced Element Redistribution in Phosphate-Based Glasses. Materials. 2020; 13(6):1275. https://doi.org/10.3390/ma13061275
Chicago/Turabian StyleMoreno-Zarate, Pedro, Francisco Muñoz, Belen Sotillo, Manuel Macias-Montero, Julia Atienzar, Marina Garcia-Pardo, Paloma Fernandez, Rosalia Serna, and Javier Solis. 2020. "Role of the La/K Compositional Ratio in the Properties of Waveguides Written by Fs-Laser Induced Element Redistribution in Phosphate-Based Glasses" Materials 13, no. 6: 1275. https://doi.org/10.3390/ma13061275
APA StyleMoreno-Zarate, P., Muñoz, F., Sotillo, B., Macias-Montero, M., Atienzar, J., Garcia-Pardo, M., Fernandez, P., Serna, R., & Solis, J. (2020). Role of the La/K Compositional Ratio in the Properties of Waveguides Written by Fs-Laser Induced Element Redistribution in Phosphate-Based Glasses. Materials, 13(6), 1275. https://doi.org/10.3390/ma13061275