Investigation on Mg3Sb2/Mg2Si Heterogeneous Nucleation Interface Using Density Functional Theory
Abstract
:1. Introduction
2. Computational Methodology
3. Bulk and Surface Properties
3.1. Bulk Properties of Mg2Si and Mg3Sb2
3.2. Surface Properties of Mg2Si(111) and Mg3Sb2(0001)
3.3. Stability of Mg2Si(111) and Mg3Sb2(0001) Surface
4. Properties of the Mg2Si/Mg3Sb2 Interface
4.1. Mg2Si(111)/Mg3Sb2(0001) Interface Model
4.2. Mg2Si(111)/Mg3Sb2(0001) Interface Stability
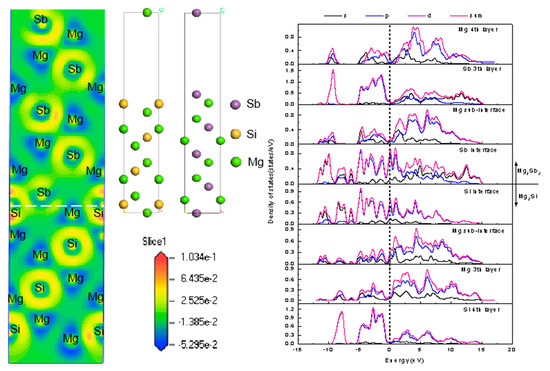
4.3. Electronic Structure and Bonding
4.4. Heterogeneous Nucleation Analysis of Mg3Sb2/Mg2Si
5. Conclusions
- (1)
- For both the Mg2Si (111) slab and the Mg3Sb2 (0001) slab, the 11-layered surface achieved bulk-like characteristics. The Sb-terminated Mg3Sb2 (0001) surface and the Si-terminated Mg2Si (111) surface were more stable than the Mg-terminated surface because of the lower surface energy.
- (2)
- Compared with all the stacking sequences, the hollow-stacked interfaces were the most stable interface. Moreover, compared with all the terminated interfaces, the Si–HCP–Sb interface was the most stable interface, because of the fact that Wad and the interface spacing of the Si–HCP–Sb interface, Si–HCP–Mg interface, Mg–HCP–Sb interface, and Mg–HCP–Mg interface were 2.54 J/m2 and 0.9 Å, 2.05 J/m2 and 1.6 Å, 1.51 J/m2 and 1.5Å, and 0.86 J/m2 and 1.3Å, respectively.
- (3)
- The chemical bonding of the Mg–HCP–Mg interfaces presented stronger metallic bonding, which exhibited the highest interfacial energy. The Mg–HCP–Sb interface and the Si–HCP–Mg interface bonding similarly exhibited a mixture of covalent and metallic bonds. In particular, the Si–HCP–Sb interfaces had an obvious strong covalent feature and the smallest interfacial energy, which showed the largest stability interface among the 12 interface models.
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Ha, S.H.; Lee, S.Y.; Yoon, Y.O.; Kim, B.H.; Lim, H.K.; Kim, S.K. Simultaneous improvement of strength and ductility in hypoeutectic Al-Si-Mg and Al-Mg alloys with high contents of Mg. Mater. Today Proc. 2019, 10, 327–331. [Google Scholar] [CrossRef]
- Linardi, E.; Haddad, R.; Lanzani, L. Stability Analysis of the Mg2Si Phase in AA 6061 Aluminum Alloy. Procedia Mater. Sci. 2012, 1, 550–557. [Google Scholar] [CrossRef] [Green Version]
- Fallah, V.; Korinek, A.; Ofori-Opoku, N.; Raeisinia, B.; Gallerneault, M.; Provatas, N.; Esmaeil, S. Atomic—scale pathway of early-stage precipitation in Al-Mg-Si alloys. Acta Mater. 2015, 82, 457–467. [Google Scholar] [CrossRef] [Green Version]
- Chrominski, W.; Lewandowska, M. Precipitation phenomena in ultrafine grained Al-Mg-Si alloy with heterogeneous microstructure. Acta Mater. 2016, 103, 547–557. [Google Scholar] [CrossRef]
- Zuo, M.; Han, H.M.; Wang, D.T.; Zhao, D.G.; Wang, Y.; Wang, Z.Q. The heterogeneous nucleation behavior of Al-Hf-P master alloy and its influence on the refinement of Mg2Si phase in Mg2Si/Al composites. Results Phys. 2017, 7, 2012–2021. [Google Scholar] [CrossRef]
- Li, C.; Wu, Y.Y.; Li, H. Morphological evolution and growth mechanism of primary Mg2Si phase in Al-Mg2Si alloys. Acta Mater. 2011, 59, 1058–1067. [Google Scholar] [CrossRef]
- Cho, J.H.; Han, S.H.; Lee, C.G. Cooling effect on microstructure and mechanical properties during friction stir welding of Al-Mg-Si aluminum alloys. Mater. Lett. 2016, 180, 157–161. [Google Scholar] [CrossRef]
- Zheng, L.W.; Nie, H.H.; Zhang, W.G.; Liang, W.; Wang, Y.D. Microstructural refinement and improvement of mechanical properties of hot-rolled Mg-3Al-Zn alloy sheets subjected to pre-extrusion and Al-Si alloying. Mater. Sci. Eng. A 2018, 722, 58–68. [Google Scholar] [CrossRef]
- Wang, L.; Qin, X.Y.; Xiong, W.; Zhu, X.G. Fabrication and mechanical properties of bulk nanocrystalline intermetallic Mg2Si. Mater. Sci. Eng. A 2007, 459, 216–222. [Google Scholar] [CrossRef]
- Frommeyer, G.; Beer, S.; Oldenburg, K. Microstructure and Mechanical Properties of Mechanically Alloyed Intermetallic Mg2Si-Al Alloys. ChemInform 1994, 25. [Google Scholar] [CrossRef]
- Chen, K.; Li, Z.Q. Effect of co-modification by Ba and Sb on the microstructure of Mg2Si / Mg - Zn - Si composite and mechanism. J. Alloys Compd. 2014, 592, 196–201. [Google Scholar] [CrossRef]
- Yu, H.C.; Wang, H.Y.; Chen, L.; Liu, F.; Wang, C.; Jiang, Q.C. Heterogeneous nucleation of Mg2Si on CaSb2 nucleus in Al-Mg-Si alloys. CrystEngComm 2015, 17, 7048–7055. [Google Scholar] [CrossRef]
- Yuan, G.Y.; Liu, Z.L.; Wang, Q.D. Microstructure refinement of Mg-Al-Zn-Si alloys. Mater. Lett. 2002, 56, 53–58. [Google Scholar] [CrossRef]
- Yu, H.C.; Wang, H.Y.; Chen, L.; Liu, F.; Wang, C.; Jiang, Q.C. Influence of Li2Sb additions on microstructure and mechanical properties of Al-20Mg2Si alloy. Materials 2016, 9, 243. [Google Scholar] [CrossRef] [Green Version]
- Hou, J.; Li, C.; Liu, X.F. Nucleating role of an effective in situ Mg3P2 on Mg2Si in Mg-Al-Si alloys. J. Alloys Compd. 2011, 509, 735–739. [Google Scholar] [CrossRef]
- Kim, J.J.; Kim, D.H.; Shin, K.S.; Kim, N.J. Modification of Mg2Si morphology in squeeze cast Mg-Al-Zn-Si alloys by Ca or P addition. Scr. Mater. 1999, 41, 333–340. [Google Scholar] [CrossRef]
- Yuan, W.H.; Liang, Z.Y.; Zhang, C.Y.; Wei, L.J. Effects of La addition on the mechanical properties and thermal-resistant properties of Al-Mg-Si-Zr alloys based on AA 6201. Mater. Des. 2011, 34, 788–792. [Google Scholar] [CrossRef]
- Hu, Z.; Ruan, X.M.; Yan, H. Effects of neodymium addition on microstructure and mechanical properties of near-eutectic Al-12Si alloys. Trans. Nonferrous Met. Soc. China 2015, 25, 3877–3885. [Google Scholar] [CrossRef]
- Khorshidi, R.; Honarbakhsh-Raouf, A.; Mahmudi, R. Microstructural evolution and high temperature mechanical properties of cast Al-15Mg2Si-xGd in situ composites. J. Alloys Compd. 2017, 700, 18–28. [Google Scholar] [CrossRef]
- Wang, H.Y.; Li, Q.; Liu, B.; Zhang, N.; Chen, L.; Wang, J.G.; Jiang, Q.C. Modification of Primary Mg2Si in Mg-4Si Alloys with Antimony. Metall. Mater. Trans. A 2012, 43, 4926–4932. [Google Scholar] [CrossRef]
- Xia, Z.; Li, K. First-principles study on Al4Sr as the heterogeneous nucleus of Mg2Si. Mater. Res. Express 2016, 3, 126503. [Google Scholar] [CrossRef]
- Wang, H.Y.; Xue, X.N.; Xu, X.Y.; Wang, C.; Chen, L.; Jiang, Q.C. Effects of doping atoms (Sb, Te, Sn, P and Bi) on the equilibrium shape of Mg2Si from first-principles calculations. CrystEngComm 2016, 18, 8599–8607. [Google Scholar] [CrossRef]
- Wang, Y.; Guo, X.F. Heterogeneous nucleation of Mg2Si and Mg2(Si,Sn) on Mg3Sb2 nucleus in Mg containing Si alloys. Mater. Chem. Phys. 2019, 223, 336–342. [Google Scholar] [CrossRef]
- Sun, J.Y.; Li, C.; Liu, X.F.; Yu, L.M.; Li, H.J.; Liu, Y.C. Investigation on AlP as the heterogeneous nucleus of Mg2Si in Al-Mg2Si alloys by experimental observation and first-principles calculation. Results Phys. 2018, 8, 146–152. [Google Scholar] [CrossRef]
- Liu, R.; Yin, X.M.; Feng, K.X.; Xu, R. First-principles calculations on Mg/TiB2 interfaces. Comput. Mater. Sci. 2018, 149, 373–378. [Google Scholar] [CrossRef]
- Zhuo, Z.; Mao, H.; Xu, H.; Fu, Y. Density functional theory study of Al/NbB2 heterogeneous nucleation interface. Appl. Surf. Sci. 2018, 456, 37–42. [Google Scholar] [CrossRef]
- Wang, H.L.; Tang, J.J.; Zhao, Y.J.; Du, J. First-principles study of Mg/Al2MgC2 heterogeneous nucleation interfaces. Appl. Surf. Sci. 2015, 355, 1091–1097. [Google Scholar] [CrossRef]
- Shi, Z.J.; Liu, S.; Zhou, Y.F.; Xing, X.L.; Ren, X.J.; Yang, Q.X. Structure and properties of YAlO3/NbC heterogeneous nucleation interface: First principles calculation and experimental research. J. Alloys Compd. 2018, 773, 264–276. [Google Scholar] [CrossRef] [Green Version]
- Bramfitt, B.L. The effect of carbide and nitride additions on the heterogeneous nucleation behavior of liquid iron. Metall. Trans. 2007, 1, 1987–1995. [Google Scholar] [CrossRef]
- Segall, M.D.; Lindan, P.J.D.; Probert, M.J. First-principles simulation, ideas, illustrations and the CASTEP code. J. Phys. Condens. Matter 2002, 14, 2717–2719. [Google Scholar] [CrossRef]
- Clark, S.J.; Segall, M.D.; Pickard, C.J. First principles methods using CASTEP. Z. Für Krist. Cryst. Mater. 2005, 220, 567–570. [Google Scholar] [CrossRef] [Green Version]
- Perdew, J.P.; Wang, Y. Accurate and simple analytic representation of the electrongas correlation energy. Phys. Rev. B Condens. Matter 1992, 45, 13244–13249. [Google Scholar] [CrossRef] [PubMed]
- Perdew, J.P.; Burke, K.; Ernzerhof, M. Generalized gradient approximation made simple. Phys. Rev. Lett. 1996, 77, 3865–3868. [Google Scholar] [CrossRef] [Green Version]
- Hao, J.H.; Guo, Z.G.; Jin, Q.H. First principles calculation of structural phase transformation in Mg2Si at high pressure. Solid State Commun. 2010, 150, 2299–2302. [Google Scholar] [CrossRef]
- Zhang, J.; Fan, Z.; Wang, Y.Q.; Zhou, B.L. Effect of cooling rate on the microstructure of hypereutectic Al-Mg2Si alloys. J. Mater. Sci. Lett. 2000, 19, 1825–1828. [Google Scholar] [CrossRef]
- Watson, L.M.; Marshall, C.A.W.; Cardoso, C.P. On the electronic structure of the semiconducting compounds Mg3Bi2 and Mg3Sb2. J. Physics. F Met. Phys. 1984, 14, 113–121. [Google Scholar] [CrossRef]
- Tamaki, H.; Sato, H.K.; Kanno, T. Isotropic Conduction Network and Defect Chemistry in Mg3+delta Sb2-Based Layered Zintl Compounds with High Thermoelectric Performance. Adv. Mater. 2016, 28, 10182–10187. [Google Scholar] [CrossRef]
- Bendavid, L.I.; Carter, E.A. First principles study of bonding, adhesion, and electronic structure at the Cu2O(111)/ZnO(1010) interface. Surf. Sci. 2013, 618, 62–71. [Google Scholar] [CrossRef]
- Rapcewicz, K.; Chen, B. Consistent methodology for calculating surface and interface energies. Phys. Rev. Ser. B 1998, 57, 7281–7291. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.B.; Yuan, X.M.; Liu, S.; Zhao, C.C.; Wang, C.X.; Zhou, Y.F.; Yang, Q.X. Investigation on WC/LaAlO3 heterogeneous nucleation interface by first-principles. J. Alloys Compd. 2017, 695, 1753–1762. [Google Scholar] [CrossRef]
- Shi, Z.J.; Shao, W.; Hu, T.S.; Zhao, C.C.; Xing, X.L.; Zhou, Y.F.; Yang, Q.X. Adhesive sliding and interfacial property of YAlO3/TiC interface: A first principles investigation. J. Alloys Compd. 2019, 805, 1052–1059. [Google Scholar] [CrossRef]
- Yang, S.-Q.; Du, J.; Zhao, Y.-J. First-principles study of ZnO/Mg heterogeneous nucleation interfaces. Mater. Res. Express 2018, 6, 28–38. [Google Scholar] [CrossRef]
- Siegel, D.J.; Louis, G.H., Jr.; Adams, J.B. Adhesion, atomic structure, and bonding at the Al(111)/α-Al2O3(0001) interface: A fifirst principles study. Phys. Rev. B 2002, 65, 085415. [Google Scholar] [CrossRef] [Green Version]
- Wang, S.; Liu, Z.; Yang, X.F.; Fan, X.; Chen, W.B.; Zhang, J.Y.; Li, D. First-principles study of the TiN(111)/ZrN(111) interface. Surf. Interface Anal. 2018, 50, 321–327. [Google Scholar] [CrossRef]
- Wang, C.; Wang, C.Y. Ni/Ni3Al interface: A density functional theory study. Appl. Surf. Sci. 2009, 255, 3669–3675. [Google Scholar] [CrossRef]
- Smit, J.R.; Zhang, W. Stoichiometric interfaces of Al and Ag with Al2O3. Acta Mater. 2000, 48, 4395–4403. [Google Scholar] [CrossRef]
- Liu, W.; Li, J.C.; Zheng, W.T.; Jiang, Q. NiAl(110)/ Cr(110) interface: A density functional theory study. Phys. Rev. B 2006, 73, 205421. [Google Scholar] [CrossRef]
- Wang, J.; Li, Y.; Xu, R. First-principles calculations on electronic structure and interfacial stability of Mg/NbB2 heterogeneous nucleation interface. Surf. Sci. 2020, 691, 38–46. [Google Scholar] [CrossRef]









| System | Method | Space Group | Elastic Constants | Lattice Constants | Bulk Modulus | Formation Energy | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|
| C11 | C12 | C13 | C44 | C66 | α/Å | c/Å | B0/GPa | Efor (eV) | |||
| Mg2Si | This work | Fmm | 13.4 | 25.3 | 47.9 | 6.365 | 6.365 | 54.3 | −2.24 | ||
| Other works | 11.6 | 23.7 | 49.534 | 6.346 | 6.346 | 55.334 | −2.39 | ||||
| Experiment | 13.2 | 26.3 | 48.535 | 6.350 | 6.350 | 57.335 | |||||
| Mg3Sb2 | This work | Pm1 | 41.5 | 86.7 | 48.5 | 16.1 | 18.9 | 4.592 | 7.272 | 43.1 | −2.12 |
| Other works | 40.436 | 84.436 | 46.736 | 15.436 | 17.636 | 4.57336 | 7.22936 | 43.936 | −2.54 | ||
| Experiment | 4.60637 | 7.29537 | 45.337 | ||||||||
| Surface | Termination | Interlayer | Slab Thickness, N | |||
|---|---|---|---|---|---|---|
| 5 | 7 | 9 | 11 | |||
| Mg2Si(111) | Mg | Δ12 | −13.2 | −12.35 | 8.79 | −8.047 |
| Δ23 | 4.53 | 7.98 | −7.96 | 7.31 | ||
| Δ34 | −1.99 | −4.68 | −1.15 | |||
| Δ45 | 0.72 | 1.43 | ||||
| Δ56 | 0.048 | |||||
| Si | Δ12 | −15.02 | −16.24 | −15.69 | −9.1 | |
| Δ23 | 7.45 | 12 | 8.46 | 3.65 | ||
| Δ34 | 0.89 | 3.4185 | 3.13 | |||
| Δ45 | −1.01 | −1.14 | ||||
| Δ56 | 0.62 | |||||
| Mg3Sb2(0001) | Mg | Δ12 | −13.52 | −12.55 | −16.3 | −11.8 |
| Δ23 | 11.24 | 11.85 | 9.22 | −8.62 | ||
| Δ34 | 8.66 | −6.23 | 1.65 | |||
| Δ45 | 2.00 | −0.65 | ||||
| Δ56 | −0.32 | |||||
| Si | Δ12 | −12.56 | 10.63 | 11.68 | 16.92 | |
| Δ23 | 7.31 | −6.31 | −5.33 | 10.96 | ||
| Δ34 | −0.57 | −4.126 | 4.43 | |||
| Δ45 | −1.23 | −1.86 | ||||
| Δ56 | −0.51 | |||||
| Termination | Stacking | Fully Relaxed | ||
|---|---|---|---|---|
| Mg2Si (111) | Mg3Sb2 (0001) | d0/Å | Wad(J/m2) | |
| Mg-Terminated | Mg-Terminated | OT | 2.6 | 0.56 |
| MT | 1.8 | 0.79 | ||
| HCP | 1.3 | 0.86 | ||
| Mg-Terminated | Sb-Terminated | OT | 2.6 | 0.77 |
| MT | 1.4 | 1.06 | ||
| HCP | 1.5 | 1.51 | ||
| Si-Terminated | Mg-Terminated | OT | 2.4 | 1.24 |
| MT | 1.8 | 1.91 | ||
| HCP | 1.6 | 2.05 | ||
| Si-Terminated | Sb-Terminated | OT | 2.2 | 1.35 |
| MT | 1.3 | 1.46 | ||
| HCP | 0.9 | 2.54 | ||
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, M.; Zhang, G.; Xu, H.; Fu, Y. Investigation on Mg3Sb2/Mg2Si Heterogeneous Nucleation Interface Using Density Functional Theory. Materials 2020, 13, 1681. https://doi.org/10.3390/ma13071681
Wang M, Zhang G, Xu H, Fu Y. Investigation on Mg3Sb2/Mg2Si Heterogeneous Nucleation Interface Using Density Functional Theory. Materials. 2020; 13(7):1681. https://doi.org/10.3390/ma13071681
Chicago/Turabian StyleWang, Mingjie, Guowei Zhang, Hong Xu, and Yizheng Fu. 2020. "Investigation on Mg3Sb2/Mg2Si Heterogeneous Nucleation Interface Using Density Functional Theory" Materials 13, no. 7: 1681. https://doi.org/10.3390/ma13071681
APA StyleWang, M., Zhang, G., Xu, H., & Fu, Y. (2020). Investigation on Mg3Sb2/Mg2Si Heterogeneous Nucleation Interface Using Density Functional Theory. Materials, 13(7), 1681. https://doi.org/10.3390/ma13071681