Evaluation of Effective Mass in InGaAsN/GaAs Quantum Wells Using Transient Spectroscopy
Abstract
:1. Introduction
2. Materials and Methods
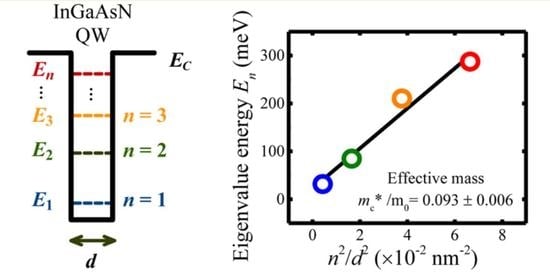
3. Results and Discussion
4. Conclusions
Supplementary Materials
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Green, M.A.; Dunlop, E.D.; Hohl-Ebinger, J.; Yoshita, M.; Kopidakis, N.; Bothe, K.; Hinken, D.; Rauer, M.; Hao, X. Solar cell efficiency tables (Version 60). Prog. Photovolt. Res. Appl. 2022, 30, 687–701. [Google Scholar] [CrossRef]
- Pastuszak, J.; Węgierek, P. Photovoltaic Cell Generations and Current Research Directions for Their Development. Materials 2022, 15, 5542. [Google Scholar] [CrossRef] [PubMed]
- Barnham, K.; Ballard, I.; Barnes, J.; Connolly, J.; Griffin, P.; Kluftinger, B.; Nelson, J.; Tsui, E.; Zachariou, A. Quantum well solar cells. Appl. Surf. Sci. 1997, 113, 722–733. [Google Scholar] [CrossRef]
- Klemmer, P.S.; Mityagin, Y.A.; Telenkov, M.P.; Nagaraja, K.K.; Elantsev, D.A.; Amiri, S. Resonant tunneling in GaAs/AlGaAs quantum well system for solar photovoltaics. Superlattices Microstruct. 2020, 140, 106472. [Google Scholar] [CrossRef]
- Rein, S. Lifetime Spectroscopy: A Method of Defect Characterisation in Silicon for Photovoltaic Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2006. [Google Scholar]
- Balcioglu, A.; Ahrenkiel, R.K.; Hasoon, F. Deep-level impurities in CdTe/CdS thin-film solar cells. J. Appl. Phys. 2000, 88, 7175–7178. [Google Scholar]
- Kim, J.W.; Song, G.H.; Lee, J.W. Observation of minority-carrier traps in In Ga N/Ga N multiple-quantum-well light-emitting diodes during deep-level transient spectroscopy measurements. Appl. Phys. Lett. 2006, 88, 182103. [Google Scholar] [CrossRef]
- Letartre, X.; Stievenard, D.; Lannoo, M.; Barbier, E. Tunnel deep level transient spectroscopy on a single quantum well. J. Appl. Phys. 1991, 69, 7336–7338. [Google Scholar] [CrossRef]
- Letartre, X.; Stievenard, D.; Barbier, E. Accurate determination of the conduction-band offset of a single quantum well using deep level transient spectroscopy. Appl. Phys. Lett. 1991, 58, 1047–1049. [Google Scholar] [CrossRef]
- Colakerol, L.; Veal, T.D.; Jeong, H.K.; Plucinski, L.; DeMasi, A.; Learmonth, T.; Glans, P.A.; Wang, S.; Zhang, Y.; Piper, L.F.; et al. Quantized electron accumulation states in indium nitride studied by angle-resolved photoemission spectroscopy. Phys. Rev. Lett. 2006, 97, 237601. [Google Scholar] [CrossRef]
- Warburton, R.J.; Michels, J.G.; Nicholas, R.J.; Harris, J.J.; Foxon, C.T. Optically detected cyclotron resonance of GaAs quantum wells: Effective-mass measurements and offset effects. Phys. Rev. B 1992, 46, 13394. [Google Scholar] [CrossRef]
- Pan, Z.; Li, L.H.; Lin, Y.W.; Sun, B.Q.; Jiang, D.S.; Ge, W.K. Conduction band offset and electron effective mass in GaInNAs/GaAs quantum-well structures with low nitrogen concentration. Appl. Phys. Lett. 2001, 78, 2217–2219. [Google Scholar] [CrossRef]
- Knolle, J.; Cooper, N.R. Anomalous de Haas–van Alphen effect in InAs/GaSb quantum wells. Phys. Rev. Lett. 2017, 118, 176801. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hatke, A.T.; Zudov, M.A.; Pfeiffer, L.N.; West, K.W. Shubnikov–de Haas oscillations in GaAs quantum wells in tilted magnetic fields. Phys. Rev. B. 2012, 85, 241305. [Google Scholar] [CrossRef] [Green Version]
- Failla, M.; Keller, J.; Scalari, G.; Maissen, C.; Faist, J.; Reichl, C.; Wegscheider, W.; Newell, O.J.; Leadley, D.R.; Myronov, M.; et al. Terahertz quantum Hall effect for spin-split heavy-hole gases in strained Ge quantum wells. New J. Phys. 2016, 18, 113036. [Google Scholar] [CrossRef]
- Gass, M.H.; Papworth, A.J.; Joyce, T.B.; Bullough, T.J.; Chalker, P.R. Measurement of the effective electron mass in GaInNAs by energy-loss spectroscopy. Appl. Phys. Lett. 2004, 84, 1453–1455. [Google Scholar] [CrossRef]
- Papež, N.; Dallaev, R.; Ţălu, Ş.; Kaštyl, J. Overview of the Current State of Gallium Arsenide-Based Solar Cells. Materials 2021, 14, 3075. [Google Scholar] [CrossRef]
- Wartak, M.S.; Weetman, P. Numerical analysis of the effective masses in InGaAsN quantum-well structures with self-consistent effects. J. Phys Cond. Matter 2005, 17, 6539. [Google Scholar] [CrossRef]
- Wartak, M.S.; Weetman, P. Characterisation of effective masses in InGaAsN quantum well structures by computer simulations. J. Appl. Phys. 2005, 98, 113705. [Google Scholar] [CrossRef]
- Skierbiszewski, C.; Łepkowski, S.P.; Perlin, P.; Suski, T.; Jantsch, W.; Geisz, J. Effective mass and conduction band dispersion of GaAsN/GaAs quantum wells. Phys. E 2002, 13, 1078–1081. [Google Scholar] [CrossRef]
- Shan, W.; Walukiewicz, W.; Yu, K.M.; Ager Iii, J.W.; Haller, E.E.; Geisz, J.F.; Friedman, D.J.; Olson, J.M.; Kurtz, S.R.; Xin, H.P.; et al. Band anticrossing in III–N–V alloys. Phys. Status Solidi B 2001, 223, 75–85. [Google Scholar] [CrossRef]
- Ściana, B.; Radziewicz, D.; Pucicki, D.; Serafińczuk, J.; Dawidowski, W.; Bielak, K.; Badura, M.; Gelczuk, Ł.; Tłaczała, M.; Latkowska, M.; et al. Influence of the AP MOVPE process parameters on properties of (In, Ga)(As, N)/GaAs heterostructures for photovoltaic applications. Electron Technol. Conf. 2013 2013, 8902, 136–143. [Google Scholar]
- Weiss, S.; Kassing, R. Deep Level Transient Fourier Spectroscopy (DLTFS)—A technique for the analysis of deep level properties. Solid-State Electron. 1988, 31, 1733–1742. [Google Scholar] [CrossRef]
- Yakimova, R.; Paskova, T.; Hardalov, C. Behavior of an EL5-like defect in metalorganic vapor-phase epitaxial GaAs: Sb. J. Appl. Phys. 1993, 74, 6170–6173. [Google Scholar] [CrossRef]
- Shiraki, H.; Tokuda, Y.; Sassa, K. Bistable behavior of a medium-deep center related to EL5 and EL6 in n-type bulk GaAs. J. Appl. Phys. 1998, 84, 3167–3174. [Google Scholar] [CrossRef]
- Weiss, S.; Beckmann, R.; Kassing, R. The Electrical Properties of Zinc in Silicon. Appl. Phys. A 1990, 50, 151–156. [Google Scholar] [CrossRef]
- Galluppi, M.; Geelhaar, L.; Riechert, H. Nitrogen and indium dependence of the band offsets in InGaAsN quantum wells. Appl. Phys. Lett. 2005, 86, 131925. [Google Scholar] [CrossRef]
- Nag, B.R. Physics of Quantum Well Devices; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2001. [Google Scholar]
- Soma, T.; Satoh, J.; Matsuo, H. Thermal expansion coefficient of GaAs and InP. Solid State Commun. 1982, 42, 889–892. [Google Scholar] [CrossRef]
- Héroux, J.B.; Yang, X.; Wang, W.I. Optical characterization of strained InGaAsN/GaAs multiple quantum wells. Vac. Sci. Technol. B 2002, 20, 1154–1157. [Google Scholar] [CrossRef]
- Ardali, S.; Tiras, E.; Erol, A. Integer quantum Hall effect measurement analysis in Ga0. 68In0. 32N0. 017As/GaAs quantum wells with various annealing time. Phys. B Condens. Matter 2021, 621, 413305. [Google Scholar] [CrossRef]
- Sarcan, F.; Donmez, O.; Erol, A.; Gunes, M.; Arikan, M.C.; Puustinen, J.; Guina, M. Influence of nitrogen on hole effective mass and hole mobility in p-type modulation doped GaInNAs/GaAs quantum well structures. Appl. Phys. Lett. 2013, 103, 082121. [Google Scholar] [CrossRef]
- Baranov, P.G.; Romanov, N.G.; Preobrazhenski, V.L.; Egorova, A.Y.; Ustinov, V.M.; Sobolev, M.M. Optically-detected microwave resonance in InGaAsN/GaAs quantum wells and InAs/GaAs quantum dots emitting around 1.3 μm. Int. J. Nanosci. 2003, 2, 469–478. [Google Scholar] [CrossRef]




| Technique | Reference | |
|---|---|---|
| 0.05 ~ 0.09 (n) | RTOP | [12] |
| 0.06 ~ 0.08 (n) | RTOP | [30] |
| 0.077 ~ 0.078 (n) | QHE, SdH | [31] |
| 0.07 ~ 0.12 (p) | SdH | [32] |
| 0.07 (n) | ODCR | [33] |
| 0.093 ± 0.006 (n) | Transient spectroscopy | This work |
| 0.122 ± 0.018 (p) | Transient spectroscopy | This work |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Stuchlikova, L.; Sciana, B.; Kosa, A.; Matus, M.; Benko, P.; Marek, J.; Donoval, M.; Dawidowski, W.; Radziewicz, D.; Weis, M. Evaluation of Effective Mass in InGaAsN/GaAs Quantum Wells Using Transient Spectroscopy. Materials 2022, 15, 7621. https://doi.org/10.3390/ma15217621
Stuchlikova L, Sciana B, Kosa A, Matus M, Benko P, Marek J, Donoval M, Dawidowski W, Radziewicz D, Weis M. Evaluation of Effective Mass in InGaAsN/GaAs Quantum Wells Using Transient Spectroscopy. Materials. 2022; 15(21):7621. https://doi.org/10.3390/ma15217621
Chicago/Turabian StyleStuchlikova, Lubica, Beata Sciana, Arpad Kosa, Matej Matus, Peter Benko, Juraj Marek, Martin Donoval, Wojciech Dawidowski, Damian Radziewicz, and Martin Weis. 2022. "Evaluation of Effective Mass in InGaAsN/GaAs Quantum Wells Using Transient Spectroscopy" Materials 15, no. 21: 7621. https://doi.org/10.3390/ma15217621
APA StyleStuchlikova, L., Sciana, B., Kosa, A., Matus, M., Benko, P., Marek, J., Donoval, M., Dawidowski, W., Radziewicz, D., & Weis, M. (2022). Evaluation of Effective Mass in InGaAsN/GaAs Quantum Wells Using Transient Spectroscopy. Materials, 15(21), 7621. https://doi.org/10.3390/ma15217621