Study on Dynamic Mechanical Properties of Sandwich Beam with Stepwise Gradient Polymethacrylimide (PMI) Foam Core under Low-Velocity Impact
Abstract
:1. Introduction
2. Experimental Procedures
2.1. Materials and Specimens
2.2. Experimental Apparatus
3. Results and Discussions
3.1. Quasi-Static Load Case
3.1.1. Compressive Force–Displacement Curves
3.1.2. Energy Absorption of the Sandwich Beam under Three-Point Bending Tests
3.2. Dynamic Load Cases
3.2.1. The Impact Force–Time Curves of the Sandwich-Core 52/X/52
3.2.2. The Impact Force–Time Curves of Sandwich-Core 110/X/110
3.2.3. The Impact Force–Time Curves of Sandwich-Core 200/X/200
3.2.4. The Impact Force–Time Curves of the Positive and Negative Gradient Cores 52/110/200 and 200/110/52
3.3. Energy Absorption of the Sandwich Beam with Different Cores under Impact Loading
3.4. Deformation and Failure Mechanism
3.4.1. Deformation and Failure Mechanism of Quasi-Static Load Case
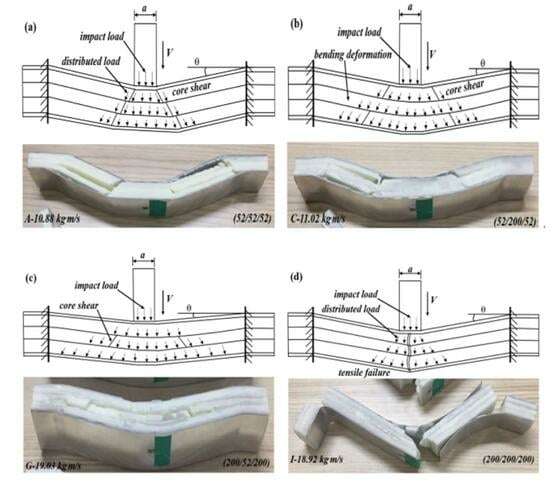
3.4.2. Deformation and Failure Mechanisms under Impact Loading
- Case 1: sandwich-core of 52/X/52, 110/X/110, and 200/X/200
- Case 2: positive gradient core (52/110/200)
- Case 3: negative gradient core (200/110/52)
4. Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Li, J.; Gao, G.; Yu, Y.; Zhuo, T. Experimental and numerical study on the lightweight design of load-bearing energy absorption structure for subway train. Thin-Walled Struct. 2024, 197, 111542. [Google Scholar] [CrossRef]
- Ghanbari, J.; Panirani, P.N. A hybrid bio-inspired sandwich structures for high strain rate energy absorption applications. Sci. Rep. 2024, 14, 2865. [Google Scholar] [CrossRef] [PubMed]
- Xiao, W.; Hu, Y.; Li, Y. Ice impact response and energy dissipation characteristics of PVC foam core sandwich plates: Experimental and numerical study. Mar. Struct. 2023, 89, 103407. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, W.; Yuan, H.; Wu, X. Failure behavior of a sandwich beam with GLARE face-sheets and aluminum foam core under three-point bending. Thin-Walled Struct. 2023, 183, 110438. [Google Scholar] [CrossRef]
- Zhao, X.; Wei, L.; Wen, D.; Zhu, G.; Yu, Q.; Ma, Z.D. Bending response and energy absorption of sandwich beams with novel auxetic honeycomb core. Eng. Struct. 2021, 247, 113204. [Google Scholar] [CrossRef]
- Khan, F.; Hossain, N.; Mim, J.J.; Rahman, S.M.; Iqbal, M.J.; Billah, M.; Chowdhury, M.A. Advances of Composite Materials in Automobile Applications—A Review. J. Eng. Res. 2024. [Google Scholar] [CrossRef]
- Zhang, J.; Huang, W.; Miao, F.; Du, J.; Sun, H. Plastic behavior of sandwich beams with fiber metal laminate face-sheets and metal foam core: Combined local denting and overall deformation. Thin-Walled Struct. 2022, 173, 108973. [Google Scholar] [CrossRef]
- Zhu, Y.; Sun, Y. Dynamic response of foam core sandwich panel with composite face sheets during low-velocity impact and penetration. Int. J. Impact Eng. 2020, 139, 103508. [Google Scholar] [CrossRef]
- Li, Z.; Gao, Y.; Wang, Y.; Xue, P.; Gong, C.; Wang, W.; Wei, X.; Xiong, J. Failure mechanisms and acoustic emission pattern recognition of all-CFRP cylindrical honeycomb sandwich shell under three-point bending. Compos. Sci. Technol. 2023, 237, 110003. [Google Scholar] [CrossRef]
- Ge, J.; Luo, T.; Qiu, J. Experimental Investigation of the Dynamic Responses of Thin-Walled and Foam-Filled Steel Tubes Subjected to Repeated Impacts. Materials 2024, 17, 1018. [Google Scholar] [CrossRef]
- Lu, H.; Wang, X.; Chen, T. Quasi-static bending response and energy absorption of a novel sandwich beam with a reinforced auxetic core under the fixed boundary at both ends. Thin-Walled Struct. 2023, 191, 111011. [Google Scholar] [CrossRef]
- Xie, H.; Li, W.; Fang, H.; Zhang, S.; Yang, Z.; Fang, Y.; Yu, F. Flexural behavior evaluation of a foam core curved sandwich beam. Compos. Struct. 2024, 328, 117729. [Google Scholar] [CrossRef]
- Zhang, W.; Li, J.; Wang, Z.; Li, K.; Bai, C.; Qin, Q. The influence of asymmetric faces on low-velocity impact failure of CFRP/aluminum foam composite sandwich beams. Eng. Struct. 2023, 292, 116574. [Google Scholar] [CrossRef]
- Mei, J.; Chen, Y.; Liu, Z.; Liu, J.; Huang, W. Experimental and theoretical study on the response of the X-frame CFRP sandwich beam under the local impulsive loading. Int. J. Impact Eng. 2024, 186, 104885. [Google Scholar] [CrossRef]
- Tan, Z.H.; Luo, H.; Long, W.; Han, X. Dynamic response of clamped sandwich beam with aluminium alloy foam core subjected to impact loading. Compos. Part B Eng. 2013, 46, 39–45. [Google Scholar] [CrossRef]
- Chen, C.; Airoldi, A.; Caporale, A.; Sala, M.; Yin, G.; Xiao, J. Impact response of composite energy absorbers based on foam-filled metallic and polymeric auxetic frames. Compos. Struct. 2024, 331, 117916. [Google Scholar] [CrossRef]
- Acanfora, V.; Zarrelli, M.; Riccio, A. Experimental and numerical assessment of the impact behaviour of a composite sandwich panel with a polymeric honeycomb core. Int. J. Impact Eng. 2023, 171, 104392. [Google Scholar] [CrossRef]
- Li, J.; Zhang, W.; Wang, Z.; Wang, Q.; Wu, T.; Qin, Q. Dynamic response and failure of CFRP Kagome lattice core sandwich panels subjected to low-velocity impact. Int. J. Impact Eng. 2023, 181, 104737. [Google Scholar] [CrossRef]
- Sun, H.; Yuan, H.; Zhang, J.; Zhang, J.; Du, J.; Huang, W. Dynamic response of multilayer sandwich beams with foam-filled trapezoidal corrugated and foam cores under low-velocity impact. J. Eng. Struct. 2023, 286, 116080. [Google Scholar] [CrossRef]
- Koohbor, B.; Ravindran, S.; Kidane, A. In situ deformation characterization of density-graded foams in quasi-static and impact loading conditions. Int. J. Impact Eng. 2021, 150, 103820. [Google Scholar] [CrossRef]
- Liu, H.; Ng, B.F. Dynamic response of density-graded foam subjected to soft impact. Compos. Struct. 2022, 284, 115145. [Google Scholar] [CrossRef]
- Astafurov, S.V.; Maier, G.G.; Melnikov, E.V.; Moskvina, V.A.; Panchenko, M.Y.; Astafurova, E.G. The strain-rate dependence of the Hall-Petch effect in two austenitic stainless steels with different stacking fault energies. Mater. Sci. Eng. A 2019, 756, 365–372. [Google Scholar] [CrossRef]
- Liu, X.; Wang, Y.; He, X.; Liu, H.; Cao, S. Deformation failure mechanism and constitutive model of gradient aluminum foam under impact loading. Compos. Struct. 2024, 327, 117684. [Google Scholar] [CrossRef]
- Yang, L.; Li, X.; Yang, L.; Lu, J.; Wang, Z.; Yang, J. Experimental and numerical analysis of dynamic response of graded PVC foam sandwich panel under impact load. Mech. Adv. Mater. Struct. 2022, 29, 5567–5578. [Google Scholar] [CrossRef]
- Kazemi, M. Experimental analysis of sandwich composite beams under three-point bending with an emphasis on the layering effects of foam core. Structures 2021, 29, 383–391. [Google Scholar] [CrossRef]
- Kazemi, M. Experimental investigation on the energy absorption characteristics of sandwich panels with layering of foam core under quasi-static punch loading. J Mech. Adv. Mater. Struct. 2022, 29, 3067–3075. [Google Scholar] [CrossRef]
- Nia, A.A.; Kazemi, M. Experimental study of ballistic resistance of sandwich targets with aluminum face-sheet and graded foam core. I.J. Sndwich Struct. Mater. 2020, 22, 461–479. [Google Scholar] [CrossRef]
- Dhaliwal, G.S.; Newaz, G.M. Flexural response of degraded polyurethane foam core sandwich beam with initial crack between face sheet and core. Materials 2020, 13, 5399. [Google Scholar] [CrossRef]
- Wang, F. Static plastic analysis of metallic sandwich beam with functionally graded core. Int. Eur. J. Mech. A/Solids 2021, 90, 104370. [Google Scholar] [CrossRef]
- Jing, L.; Su, X.; Chen, D.; Yang, F.; Zhao, L. Experimental and numerical study of sandwich beams with layered-gradient foam cores under low-velocity impact. Thin-Walled Struct. 2019, 135, 227–244. [Google Scholar] [CrossRef]
- Zhang, W.; Qin, Q.; Li, K.; Li, J.; Wang, Q. Effect of stepwise gradient on dynamic failure of composite sandwich beams with metal foam core subject to low-velocity impact. Int. J. Solids Struct. 2021, 228, 111125. [Google Scholar] [CrossRef]
- Fang, B.; Huang, W.; Xu, H.; Jiang, C.; Liu, J. High-velocity impact resistance of stepwise gradient sandwich beams with metal foam cores. Thin-Walled Struct. 2022, 181, 110054. [Google Scholar] [CrossRef]
- Zhao, Z.; Jing, L. The response of clamped sandwich panels with layered-gradient aluminum foam cores to foam projectile impact. Mech. Adv. Mater. Struct. 2020, 27, 744–753. [Google Scholar] [CrossRef]
- Khaire, N.; Gupta, M.; Tiwari, G. Blast resistance of graded aluminium foam core sandwich structure against blast loading. Mater. Today Proc. 2023, 87, 159–163. [Google Scholar] [CrossRef]
- Khondabi, R.; Khodarahmi, H.; Hosseini, R.; Ziya-Shamami, M. Dynamic plastic response of sandwich structures with graded polyurethane foam cores and metallic face sheets exposed to uniform blast loading: Experimental study and numerical simulation. J. Braz. Soc. Mech. Sci. Eng. 2023, 45, 526. [Google Scholar] [CrossRef]
- Flores-Johnson, E.; Li, Q. Experimental study of the indentation of sandwich panels with carbon fibre-reinforced polymer face sheets and polymeric foam core. Compos. Part B Eng. 2011, 42, 1212–1219. [Google Scholar] [CrossRef]
- Cheon, S.; Yu, S.; Kim, K.-Y.; Lim, D.Y.; Lee, J.-C. Improvement of Interfacial Bonding Force between PMI Foam and CFRP in PMI Foam-Cored CFRP Sandwich Composites. Fibers Polym. 2021, 22, 2281–2284. [Google Scholar] [CrossRef]
- Huo, X.; Jiang, Z.; Luo, Q.; Li, Q.; Sun, G. Mechanical characterization and numerical modeling on the yield and fracture behaviors of polymethacrylimide (PMI) foam materials. Int. J. Mech. Sci. 2022, 218, 107033. [Google Scholar] [CrossRef]
- Song, S.; Xiong, C.; Zheng, J.; Yin, J.; Zou, Y.; Zhu, X. Compression, bending, energy absorption properties, and failure modes of composite Kagome honeycomb sandwich structure reinforced by PMI foams. Compos. Struct. 2021, 277, 114611. [Google Scholar] [CrossRef]
- Mahgoub, M.; Zhang, Y.; Yang, C.; Tan, Z.H. Dynamic Responses of Sandwich Beams with Polymethacrylimide (PMI) Foam Cores When Subjected to Impact Loading. Materials 2023, 16, 1108. [Google Scholar] [CrossRef]
- Zhou, H.; Liu, R.; Hu, Y.; Song, P.; Guo, R. Quasi-static compressive strength of polymethacrylimide foam-filled square carbon fiber reinforced composite honeycombs. J. Sandw. Struct. Mater. 2021, 23, 2358–2374. [Google Scholar] [CrossRef]
- Wang, F.; Ming, Y.; Zhao, Y.; Yang, F.; Lou, J.; Zhu, Y.; Duan, Y.; Wang, B.; Xiao, H. Fabrication of a novel continuous fiber 3D printed thermoset all-composite honeycomb sandwich structure with polymethacrylimide foam reinforcement. J. Compos. Commun. 2024, 45, 101794. [Google Scholar] [CrossRef]
- Suzhou Zhongbao Composite Material Co., Ltd., Suzhou, China. Available online: http://www.szzbmf.com (accessed on 6 June 2023).
- Lutai Co., Ltd., Suzhou, China. Available online: http://www.lttc.com.cn (accessed on 6 June 2023).
- Kaboglu, C.; Yu, L.; Mohagheghian, I.; Blackman, B.R.; Kinloch, A.J.; Dear, J.P. Effects of the core density on the quasi-static flexural and ballistic performance of fibre-composite skin/foam-core sandwich structures. J. Mater. Sci. 2018, 53, 16393–16414. [Google Scholar] [CrossRef]
- Yuan, H.; Zhang, J.; Sun, H. The failure behavior of double-layer metal foam sandwich beams under three-point bending. Thin-Walled Struct. 2022, 180, 109801. [Google Scholar] [CrossRef]
- Zhao, Y.; Yang, Z.; Yu, T.; Xin, D. Mechanical properties and energy absorption capabilities of aluminium foam sandwich structure subjected to low-velocity impact. Constr. Build. Mater. 2021, 273, 121996. [Google Scholar] [CrossRef]
- Shunmugasamy, V.C.; Mansoor, B. Aluminum foam sandwich with density-graded open-cell core: Compressive and flexural response. Mater. Sci. Eng. A 2018, 731, 220–230. [Google Scholar] [CrossRef]















| No. | Specimen Code | Thickness of Each Layer (mm) | Density of the Core Layer (kg/m3) | Average Density of the Core (kg/m3) |
|---|---|---|---|---|
| 1 | A | 0.5/5/5/5/0.5 | 52/52/52 | 52 |
| 2 | B | 0.5/5/5/5/0.5 | 52/110/52 | 71 |
| 3 | C | 0.5/5/5/5/0.5 | 52/200/52 | 101 |
| 4 | D | 0.5/5/5/5/0.5 | 110/52/110 | 91 |
| 5 | E | 0.5/5/5/5/0.5 | 110/110/110 | 110 |
| 6 | F | 0.5/5/5/5/0.5 | 110/200/110 | 140 |
| 7 | G | 0.5/5/5/5/0.5 | 200/52/200 | 151 |
| 8 | H | 0.5/5/5/5/0.5 | 200/110/200 | 170 |
| 9 | I | 0.5/5/5/5/0.5 | 200/200/200 | 200 |
| 10 | P | 0.5/5/5/5/0.5 | 52/110/200 | 121 |
| 11 | N | 0.5/5/5/5/0.5 | 200/110/52 | 121 |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Mahgoub, M.; Liu, C.; Tan, Z. Study on Dynamic Mechanical Properties of Sandwich Beam with Stepwise Gradient Polymethacrylimide (PMI) Foam Core under Low-Velocity Impact. Materials 2024, 17, 2099. https://doi.org/10.3390/ma17092099
Mahgoub M, Liu C, Tan Z. Study on Dynamic Mechanical Properties of Sandwich Beam with Stepwise Gradient Polymethacrylimide (PMI) Foam Core under Low-Velocity Impact. Materials. 2024; 17(9):2099. https://doi.org/10.3390/ma17092099
Chicago/Turabian StyleMahgoub, Mousab, Cong Liu, and Zhuhua Tan. 2024. "Study on Dynamic Mechanical Properties of Sandwich Beam with Stepwise Gradient Polymethacrylimide (PMI) Foam Core under Low-Velocity Impact" Materials 17, no. 9: 2099. https://doi.org/10.3390/ma17092099
APA StyleMahgoub, M., Liu, C., & Tan, Z. (2024). Study on Dynamic Mechanical Properties of Sandwich Beam with Stepwise Gradient Polymethacrylimide (PMI) Foam Core under Low-Velocity Impact. Materials, 17(9), 2099. https://doi.org/10.3390/ma17092099