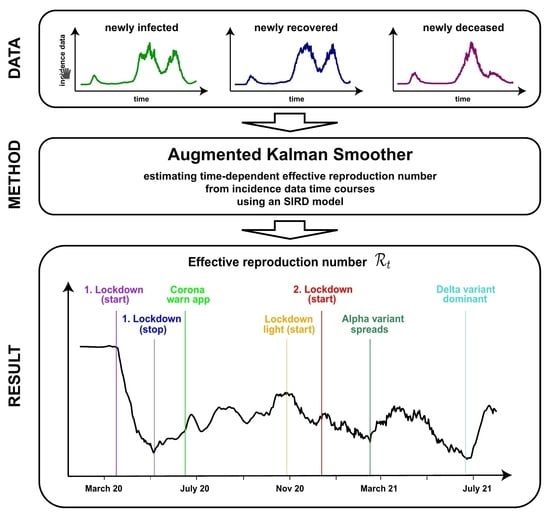
Non-Parametric Model-Based Estimation of the Effective Reproduction Number for SARS-CoV-2 †
Abstract
:1. Introduction
2. Materials and Methods
2.1. SIRD Model and Reparameterization
2.2. Estimation of Time-Dependent Parameters in Non-Linear ODE Models via the Augmented Kalman Smoother
2.2.1. State-Space Model
2.2.2. Augmented Kalman Smoother
2.2.3. Expectation-Maximization Algorithm for AKS Initial Parameters
| Algorithm 1 Augmented Kalman Smoother (AKS) | ||
| 1: | procedure AKS() | |
| 2: | ▹Data processing | |
| 3: | ||
| 4: | ▹ Model parameters and initial values | |
| 5: | observation_matrix() | |
| 6: | initial_state_vector_guess() | |
| 7: | initial_state_covariance_guess() | |
| 8: | initialize_state_covariance() | |
| 9: | initial_evolution_error_guess() | |
| 10: | initial_observation_error_guess() | |
| 11: | ▹AKS initialization | |
| 12: | ||
| 13: | ||
| 14: | ||
| 15: | ||
| 16: | ▹Main loop for AKS | |
| 17: | while do | |
| 18: | ▹ Predict state-space vectors and covariance matrices | |
| 19: | AKF_Prediction() | [Equations (6)–(8)] |
| 20: | ▹Filter state-space vectors and covariance matrices | |
| 21: | AKF_Update() | [Equations (9)–(11)] |
| 22: | ▹ Smooth state-space vectors and covariance matrices | |
| 23: | AKS_Smoother() | [Equations (12)–(14)] |
| 24: | ▹Perform M-step for parameter estimation | |
| 25: | M_step() | [Equations (15) and (16)] |
| 26: | ▹Update AKS variables | |
| 27: | update_AKS_variables() | |
| 28: | ▹Check convergence criterion | |
| 29: | check_convergence() | [Equation (17)] |
| 30: | end while | |
| 31: | ▹Return results | |
| 32: | return smoothed_results | |
| 33: | end procedure | |
2.2.4. From the Time-Continuous ODE System to Its Time-Discrete State-Space Formulation
2.3. SIRD-AKS Method for Estimating the Effective Reproduction Number
2.4. Incidence-Based Reproduction-Number-Calculation Method
2.5. Simulation Setting
3. Results
3.1. AKS Performance for Multiple Time-Varying SIRD Model Parameters
3.2. Performance for High Noise Levels
3.3. Influence of Potential Model Misspecifications
3.4. Application to SARS-CoV-2 Data from Germany

3.5. Validation of Parameter Time-Course Estimates in an ODE Model
4. Discussion
5. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
References
- Jones, K.E.; Patel, N.G.; Levy, M.A.; Storeygard, A.; Balk, D.; Gittleman, J.L.; Daszak, P. Global trends in emerging infectious diseases. Nature 2008, 451, 990–993. [Google Scholar] [CrossRef]
- World Health Organization. Vector-Borne Diseases; Technical Report; WHO Regional Office for South-East Asia: New Delhi, India, 2014. [Google Scholar]
- Hethcote, H.W. The mathematics of infectious diseases. SIAM Rev. 2000, 42, 599–653. [Google Scholar] [CrossRef]
- Murray, J.D. Mathematical Biology: I. An Introduction. Interdisciplinary Applied Mathematics; Springer: Berlin/Heidelberg, Germany, 2002. [Google Scholar]
- Brauer, F.; Castillo-Chavez, C.; Castillo-Chavez, C. Mathematical Models in Population Biology and Epidemiology; Springer: Berlin/Heidelberg, Germany, 2012; Volume 2. [Google Scholar]
- Tönsing, C.; Timmer, J.; Kreutz, C. Profile likelihood-based analyses of infectious disease models. Stat. Methods Med. Res. 2018, 27, 1979–1998. [Google Scholar] [CrossRef]
- Abboubakar, H.; Guidzavaï, A.K.; Yangla, J.; Damakoa, I.; Mouangue, R. Mathematical modeling and projections of a vector-borne disease with optimal control strategies: A case study of the Chikungunya in Chad. Chaos Solitons Fractals 2021, 150, 111197. [Google Scholar] [CrossRef]
- Barbarossa, M.V.; Fuhrmann, J.; Meinke, J.H.; Krieg, S.; Varma, H.V.; Castelletti, N.; Lippert, T. Modeling the spread of COVID-19 in Germany: Early assessment and possible scenarios. PLoS ONE 2020, 15, e0238559. [Google Scholar] [CrossRef]
- Dehning, J.; Zierenberg, J.; Spitzner, F.P.; Wibral, M.; Neto, J.P.; Wilczek, M.; Priesemann, V. Inferring change points in the spread of COVID-19 reveals the effectiveness of interventions. Science 2020, 369, eabb9789. [Google Scholar] [CrossRef]
- Bai, Z.; Gong, Y.; Tian, X.; Cao, Y.; Liu, W.; Li, J. The rapid assessment and early warning models for COVID-19. Virol. Sin. 2020, 35, 272–279. [Google Scholar] [CrossRef]
- Ferguson, N.; Laydon, D.; Nedjati Gilani, G.; Imai, N.; Ainslie, K.; Baguelin, M.; Bhatia, S.; Boonyasiri, A.; Cucunuba Perez, Z.; Cuomo-Dannenburg, G.; et al. Report 9: Impact of Non-Pharmaceutical Interventions (NPIs) to Reduce COVID-19 Mortality and Healthcare Demand; Imperial College London: London, UK, 2020. [Google Scholar]
- Jarvis, C.I.; Van Zandvoort, K.; Gimma, A.; Prem, K.; Klepac, P.; Rubin, G.J.; Edmunds, W.J. Quantifying the impact of physical distance measures on the transmission of COVID-19 in the UK. BMC Med. 2020, 18, 1–10. [Google Scholar] [CrossRef]
- Latsuzbaia, A.; Herold, M.; Bertemes, J.P.; Mossong, J. Evolving social contact patterns during the COVID-19 crisis in Luxembourg. PLoS ONE 2020, 15, e0237128. [Google Scholar] [CrossRef]
- Ivorra, B.; Ferrández, M.R.; Vela-Pérez, M.; Ramos, A.M. Mathematical modeling of the spread of the coronavirus disease 2019 (COVID-19) taking into account the undetected infections. The case of China. Commun. Nonlinear Sci. Numer. Simul. 2020, 88, 105303. [Google Scholar] [CrossRef]
- Contento, L.; Castelletti, N.; Raimundez, E.; Le Gleut, R.; Schaelte, Y.; Stapor, P.; Hinske, L.C.; Hoelscher, M.; Wieser, A.; Radon, K.; et al. Integrative modelling of reported case numbers and seroprevalence reveals time-dependent test efficiency and infection rates. medRxiv 2021. [Google Scholar]
- Rockett, R.J.; Arnott, A.; Lam, C.; Sadsad, R.; Timms, V.; Gray, K.A.; Eden, J.S.; Chang, S.; Gall, M.; Draper, J.; et al. Revealing COVID-19 transmission in Australia by SARS-CoV-2 genome sequencing and agent-based modeling. Nat. Med. 2020, 26, 1398–1404. [Google Scholar] [CrossRef]
- Truszkowska, A.; Behring, B.; Hasanyan, J.; Zino, L.; Butail, S.; Caroppo, E.; Jiang, Z.P.; Rizzo, A.; Porfiri, M. High-resolution agent-based modeling of COVID-19 spreading in a small town. Adv. Theory Simul. 2021, 4, 2000277. [Google Scholar] [CrossRef]
- Hoertel, N.; Blachier, M.; Blanco, C.; Olfson, M.; Massetti, M.; Rico, M.S.; Limosin, F.; Leleu, H. A stochastic agent-based model of the SARS-CoV-2 epidemic in France. Nat. Med. 2020, 26, 1417–1421. [Google Scholar] [CrossRef]
- Capaldi, A.; Behrend, S.; Berman, B.; Smith, J.; Wright, J.; Lloyd, A.L. Parameter estimation and uncertainty quantication for an epidemic model. Math. Biosci. Eng. 2012, 9, 553. [Google Scholar]
- Kermack, W.O.; McKendrick, A.G. Contributions to the mathematical theory of epidemics–I. 1927. Bull. Math. Biol. 1991, 53, 33–55. [Google Scholar]
- Chen, X.; Li, J.; Xiao, C.; Yang, P. Numerical solution and parameter estimation for uncertain SIR model with application to COVID-19. Fuzzy Optim. Decis. Mak. 2021, 20, 189–208. [Google Scholar] [CrossRef]
- Bani-Yaghoub, M.; Gautam, R.; Shuai, Z.; Van Den Driessche, P.; Ivanek, R. Reproduction numbers for infections with free-living pathogens growing in the environment. J. Biol. Dyn. 2012, 6, 923–940. [Google Scholar] [CrossRef]
- Wieland, F.G.; Hauber, A.L.; Rosenblatt, M.; Tönsing, C.; Timmer, J. On structural and practical identifiability. Curr. Opin. Syst. Biol. 2021, 25, 60–69. [Google Scholar] [CrossRef]
- Massonis, G.; Banga, J.R.; Villaverde, A.F. Structural identifiability and observability of compartmental models of the COVID-19 pandemic. Annu. Rev. Control. 2020, 51, 441–459. [Google Scholar] [CrossRef]
- Godio, A.; Pace, F.; Vergnano, A. SEIR modeling of the Italian epidemic of SARS-CoV-2 using computational swarm intelligence. Int. J. Environ. Res. Public Health 2020, 17, 3535. [Google Scholar] [CrossRef]
- Raimúndez, E.; Dudkin, E.; Vanhoefer, J.; Alamoudi, E.; Merkt, S.; Fuhrmann, L.; Bai, F.; Hasenauer, J. COVID-19 outbreak in Wuhan demonstrates the limitations of publicly available case numbers for epidemiological modeling. Epidemics 2021, 34, 100439. [Google Scholar] [CrossRef]
- Khailaie, S.; Mitra, T.; Bandyopadhyay, A.; Schips, M.; Mascheroni, P.; Vanella, P.; Lange, B.; Binder, S.C.; Meyer-Hermann, M. Development of the reproduction number from coronavirus SARS-CoV-2 case data in Germany and implications for political measures. BMC Med. 2021, 19, 1–16. [Google Scholar] [CrossRef]
- Rahmandad, H.; Lim, T.Y.; Sterman, J. Behavioral dynamics of COVID-19: Estimating under-reporting, multiple waves, and adherence fatigue across 92 nations. Syst. Dyn. Rev. 2021, 37, 5–31. [Google Scholar] [CrossRef]
- Prodanov, D. Analytical parameter estimation of the SIR epidemic model. Applications to the COVID-19 pandemic. Entropy 2021, 23, 59. [Google Scholar] [CrossRef]
- Jo, H.; Son, H.; Hwang, H.J.; Jung, S.Y. Analysis of COVID-19 spread in South Korea using the SIR model with time-dependent parameters and deep learning. medRxiv 2020. [Google Scholar]
- Hong, H.G.; Li, Y. Estimation of time-varying reproduction numbers underlying epidemiological processes: A new statistical tool for the COVID-19 pandemic. PLoS ONE 2020, 15, e0236464. [Google Scholar] [CrossRef]
- Kolokolnikov, T.; Iron, D. Law of mass action and saturation in SIR model with application to coronavirus modelling. Infect. Dis. Model. 2021, 6, 91–97. [Google Scholar] [CrossRef]
- Capistrán, M.A.; Moreles, M.A.; Lara, B. Parameter estimation of some epidemic models. The case of recurrent epidemics caused by respiratory syncytial virus. Bull. Math. Biol. 2009, 71, 1890–1901. [Google Scholar] [CrossRef]
- Merow, C.; Urban, M.C. Seasonality and uncertainty in global COVID-19 growth rates. Proc. Natl. Acad. Sci. USA 2020, 117, 27456–27464. [Google Scholar] [CrossRef]
- Refisch, L.; Lorenz, F.; Riedlinger, T.; Taubenböck, H.; Fischer, M.; Grabenhenrich, L.; Wolkewitz, M.; Binder, H.; Kreutz, C. Data-driven prediction of COVID-19 cases in Germany for decision making. BMC Med. Res. Methodol. 2022, 22, 1–13. [Google Scholar] [CrossRef]
- Kaschek, D.; Timmer, J. A variational approach to parameter estimation in ordinary differential equations. BMC Syst. Biol. 2012, 6, 1–8. [Google Scholar] [CrossRef]
- Engelhardt, B.; Frőhlich, H.; Kschischo, M. Learning (from) the errors of a systems biology model. Sci. Rep. 2016, 6, 20772. [Google Scholar] [CrossRef]
- Villaverde, A.F.; Tsiantis, N.; Banga, J.R. Full observability and estimation of unknown inputs, states and parameters of nonlinear biological models. J. R. Soc. Interface 2019, 16, 20190043. [Google Scholar] [CrossRef]
- Kreutz, C. A new approximation approach for transient differential equation models. Front. Phys. 2020, 8, 70. [Google Scholar] [CrossRef]
- Camacho, A.; Cazelles, B. Does homologous reinfection drive multiple-wave influenza outbreaks? Accounting for immunodynamics in epidemiological models. Epidemics 2013, 5, 187–196. [Google Scholar] [CrossRef]
- Camacho, A.; Kucharski, A.; Funk, S.; Breman, J.; Piot, P.; Edmunds, W. Potential for large outbreaks of Ebola virus disease. Epidemics 2014, 9, 70–78. [Google Scholar] [CrossRef]
- Dureau, J.; Kalogeropoulos, K.; Vickerman, P.; Pickles, M.; Boily, M.C. A Bayesian approach to estimate changes in condum use from limited human immunodeficiency virus prevalence data. J. R. Stat. Soc. Ser. C 2016, 65, 237–257. [Google Scholar] [CrossRef]
- Yang, W.; Karspeck, A.; Shaman, J. Comparison of Filtering Methods for the Modeling and Retrospective Forecasting of Influenza Epidemics. PLoS Comput. Biol. 2014, 10, 1–15. [Google Scholar] [CrossRef]
- Cazelles, B.; Champagne, C.; Nguyen-Van-Yen, B.; Comiskey, C.; Vergu, E.; Roche, B. A mechanistic and data-driven reconstruction of the time-varying reproduction number: Application to the COVID-19 epidemic. PLoS Comput. Biol. 2021, 17, 1–20. [Google Scholar] [CrossRef]
- Dureau, J.; Kalogeropoulos, K.; Baguelin, M. Capturing the time-varying drivers of an epidemic using stochastic dynamical systems. Biostatistics 2013, 14, 541–555. [Google Scholar] [CrossRef]
- Endo, A.; van Leeuwen, E.; Baguelin, M. Introduction to particle Markov-chain Monte Carlo for disease dynamics modellers. Epidemics 2019, 29, 100363. [Google Scholar] [CrossRef]
- Raanes, P.N. On the ensemble Rauch-Tung-Striebel smoother and its equivalence to the ensemble Kalman smoother. Q. J. R. Meteorol. Soc. 2016, 142, 1259–1264. [Google Scholar] [CrossRef]
- Hasan, A.; Susanto, H.; Tjahjono, V.; Kusdiantara, R.; Putri, E.; Nuraini, N.; Hadisoemarto, P. A new estimation method for COVID-19 time-varying reproduction number using active cases. Sci. Rep. 2022, 12, 6675. [Google Scholar] [CrossRef]
- Shumway, R.H.; Stoffer, D.S. An approach to time series smoothing and forecasting using the em algorithm. J. Time Ser. Anal. 1982, 3, 253–264. [Google Scholar] [CrossRef]
- Pulido, M.; Tandeo, P.; Bocquet, M.; Carrassi, A.; Lucini, M. Stochastic parameterization identification using ensemble Kalman filtering combined with maximum likelihood methods. Tellus A Dyn. Meteorol. Oceanogr. 2018, 70, 1442099. [Google Scholar] [CrossRef]
- Hermes, J.; Rosenblatt, M.; Tönsing, C.; Timmer, J. Non-parametric model-based estimation of the effective reproduction number for SARS-CoV-2. AIP Conf. Proc. 2023, 2872, 030006. [Google Scholar] [CrossRef]
- Keeling, M.J.; Rohani, P. Modeling Infectious Diseases in Humans and Animals; Princeton University Press: Princeton, NJ, USA, 2011. [Google Scholar]
- Nishiura, H.; Chowell, G. The effective reproduction number as a prelude to statistical estimation of time-dependent epidemic trends. In Mathematical and Statistical Estimation Approaches in Epidemiology; Springer: Berlin/Heidelberg, Germany, 2009; pp. 103–121. [Google Scholar]
- Raue, A.; Schilling, M.; Bachmann, J.; Matteson, A.; Schelke, M.; Kaschek, D.; Hug, S.; Kreutz, C.; Harms, B.D.; Theis, F.J.; et al. Lessons learned from quantitative dynamical modeling in systems biology. PLoS ONE 2013, 8, e74335. [Google Scholar] [CrossRef]
- Raue, A.; Steiert, B.; Schelker, M.; Kreutz, C.; Maiwald, T.; Hass, H.; Vanlier, J.; Tönsing, C.; Adlung, L.; Engesser, R.; et al. Data2Dynamics: A modeling environment tailored to parameter estimation in dynamical systems. Bioinformatics 2015, 31, 3558–3560. [Google Scholar] [CrossRef]
- Stapor, P.; Weindl, D.; Ballnus, B.; Hug, S.; Loos, C.; Fiedler, A.; Krause, S.; Hroß, S.; Fröhlich, F.; Hasenauer, J. PESTO: Parameter estimation toolbox. Bioinformatics 2018, 34, 705–707. [Google Scholar] [CrossRef]
- Loos, C.; Krause, S.; Hasenauer, J. Hierarchical optimization for the efficient parametrization of ODE models. Bioinformatics 2018, 34, 4266–4273. [Google Scholar] [CrossRef]
- Kaschek, D.; Mader, W.; Fehling-Kaschek, M.; Rosenblatt, M.; Timmer, J. Dynamic modeling, parameter estimation, and uncertainty analysis in R. J. Stat. Softw. 2019, 88, 1–32. [Google Scholar] [CrossRef]
- Schelker, M.; Raue, A.; Timmer, J.; Kreutz, C. Comprehensive estimation of input signals and dynamics in biochemical reaction networks. Bioinformatics 2012, 28, i529–i534. [Google Scholar] [CrossRef]
- Kalman, R.E. A new approach to linear filtering and prediction problems. J. Basic Eng. 1960, 82, 35–45. [Google Scholar] [CrossRef]
- Carrassi, A.; Vannitsem, S. State and parameter estimation with the extended Kalman filter: An alternative formulation of the model error dynamics. Q. J. R. Meteorol. Soc. 2011, 137, 435–451. [Google Scholar] [CrossRef]
- Sun, X.; Jin, L.; Xiong, M. Extended Kalman filter for estimation of parameters in nonlinear state-space models of biochemical networks. PLoS ONE 2008, 3, e3758. [Google Scholar] [CrossRef]
- Rauch, H.E.; Tung, F.; Striebel, C.T. Maximum likelihood estimates of linear dynamic systems. AIAA J. 1965, 3, 1445–1450. [Google Scholar] [CrossRef]
- Dreano, D.; Tandeo, P.; Pulido, M.; Ait-El-Fquih, B.; Chonavel, T.; Hoteit, I. Estimating model-error covariances in nonlinear state-space models using Kalman smoothing and the Expectation-Maximization algorithm. Q. J. R. Meteorol. Soc. 2017, 143, 1877–1885. [Google Scholar] [CrossRef]
- Cori, A.; Ferguson, N.M.; Fraser, C.; Cauchemez, S. A new framework and software to estimate time-varying reproduction numbers during epidemics. Am. J. Epidemiol. 2013, 178, 1505–1512. [Google Scholar] [CrossRef]
- der Heiden, M.; Hamouda, O. Schätzung der Aktuellen Entwicklung der SARS-CoV-2-Epidemie in Deutschland–Nowcasting. 2020. Available online: https://edoc.rki.de/handle/176904/6650.4 (accessed on 12 November 2021).
- Soetaert, K.; Petzoldt, T.; Setzer, R.W. Solving differential equations in R: Package deSolve. J. Stat. Softw. 2010, 33, 1–25. [Google Scholar] [CrossRef]
- Van den Driessche, P. Reproduction numbers of infectious disease models. Infect. Dis. Model. 2017, 2, 288–303. [Google Scholar] [CrossRef]
- Xin, H.; Li, Y.; Wu, P.; Li, Z.; Lau, E.H.Y.; Qin, Y.; Wang, L.; Cowling, B.J.; Tsang, T.K.; Li, Z. Estimating the Latent Period of Coronavirus Disease 2019 (COVID-19). Clin. Infect. Dis. 2021, 74, 1678–1681. [Google Scholar] [CrossRef]
- Dong, E.; Du, H.; Gardner, L. An interactive web-based dashboard to track COVID-19 in real time. Lancet Infect. Dis. 2020, 20, 533–534. [Google Scholar] [CrossRef]
- Staerk, C.; Wistuba, T.; Mayr, A. Estimating effective infection fatality rates during the course of the COVID-19 pandemic in Germany. BMC Public Health 2021, 21, 1073. [Google Scholar] [CrossRef]
- Yanez, N.D.; Weiss, N.S.; Romand, J.A.; Treggiari, M.M. COVID-19 mortality risk for older men and women. BMC Public Health 2020, 20, 1742. [Google Scholar] [CrossRef]
- Ho, F.K.; Petermann-Rocha, F.; Gray, S.R.; Jani, B.D.; Katikireddi, S.V.; Niedzwiedz, C.L.; Foster, H.; Hastie, C.E.; Mackay, D.F.; Gill, J.M.; et al. Is older age associated with COVID-19 mortality in the absence of other risk factors? General population cohort study of 470,034 participants. PLoS ONE 2020, 15, e0241824. [Google Scholar] [CrossRef]
- Höhle, M.; an der Heiden, M. Bayesian nowcasting during the STEC O104: H4 outbreak in Germany, 2011. Biometrics 2014, 70, 993–1002. [Google Scholar] [CrossRef]
- Fazit Communication GmbH. The Federal Government Informs about the Corona Crisis. 2021. Available online: https://www.deutschland.de/en/news/german-federal-government-informs-about-the-corona-crisis (accessed on 22 October 2021).
- Arroyo-Marioli, F.; Bullano, F.; Kucinskas, S.; Rondón-Moreno, C. Tracking R of COVID-19: A new real-time estimation using the Kalman filter. PLoS ONE 2021, 16, e0244474. [Google Scholar] [CrossRef]
- Ali, S.T.; Wang, L.; Lau, E.H.; Xu, X.K.; Du, Z.; Wu, Y.; Leung, G.M.; Cowling, B.J. Serial interval of SARS-CoV-2 was shortened over time by nonpharmaceutical interventions. Science 2020, 369, 1106–1109. [Google Scholar] [CrossRef]





Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Hermes, J.; Rosenblatt, M.; Tönsing, C.; Timmer, J. Non-Parametric Model-Based Estimation of the Effective Reproduction Number for SARS-CoV-2. Algorithms 2023, 16, 533. https://doi.org/10.3390/a16120533
Hermes J, Rosenblatt M, Tönsing C, Timmer J. Non-Parametric Model-Based Estimation of the Effective Reproduction Number for SARS-CoV-2. Algorithms. 2023; 16(12):533. https://doi.org/10.3390/a16120533
Chicago/Turabian StyleHermes, Jacques, Marcus Rosenblatt, Christian Tönsing, and Jens Timmer. 2023. "Non-Parametric Model-Based Estimation of the Effective Reproduction Number for SARS-CoV-2" Algorithms 16, no. 12: 533. https://doi.org/10.3390/a16120533
APA StyleHermes, J., Rosenblatt, M., Tönsing, C., & Timmer, J. (2023). Non-Parametric Model-Based Estimation of the Effective Reproduction Number for SARS-CoV-2. Algorithms, 16(12), 533. https://doi.org/10.3390/a16120533