Frequent Errors in Modeling by Machine Learning: A Prototype Case of Predicting the Timely Evolution of COVID-19 Pandemic
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
2.2. Models to Be Compared
2.3. Algorithms for Searching Global Minimum
2.4. Fair Method (Model) Comparison
3. Results and Discussion
3.1. Contradictions in Abstract, Discussion and Conclusion
3.2. Model Comparison
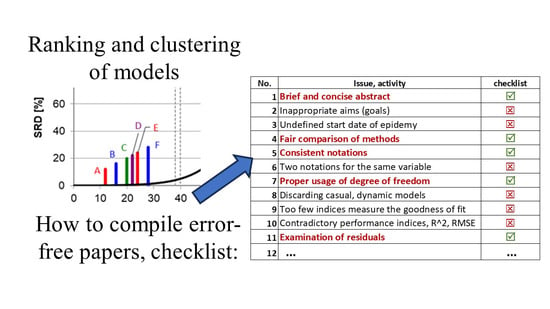
3.3. Model Comparison by Sum of Ranking Differences
3.4. Visual Inspection
3.5. Performance Parameters (Merits) and Model Discrimination
3.6. Variance Analysis of RMSEs
3.7. ANOVA of SRD for Algorithm Combinations
3.8. Reproducibility and Precision
3.9. Consistent Notations, Physical Dimensions and Units
3.10. Data Preprocessing
3.11. Orientation Table (Checklist)
4. Recommendations
4.1. Reproducibility
4.2. Precision
4.3. Validation
4.4. Training-Test Set Splits
4.5. Allocation
4.6. Terminology
4.7. Title
4.8. Abbreviations
4.9. References
4.10. Language
4.11. Out of Scope
4.12. Novelty
4.13. Note Added in Proof
5. Summary and Conclusions
6. Other Approaches (Outlook, Perspective)
- (i)
- Numerous machine learning models were developed using plenty of performance measures (90–98%) to forecast the length of stay (LOS) and mortality rate of a patient admitted to hospital. Ensemble learning increases machine learning’s performance if many classifiers provide contradictory findings [75]. The detailed review enumerates data cleaning, outlier detection, standardization, handling of missing data, stratified k-fold cross-validation, encoder handling, >eight performance parameters, etc. However, the formula for the coefficient of determination is erroneous (Equation (20)), and the frequent 100% performance suggests a probable overfit [75].
- (ii)
- The predictive accuracy to predict the length of stay in a hospital has been compared for four machine learning algorithms: DT classifier, RF, ANN, and logistic regression [76]. While the data gathering, preprocessing, and feature selection can be assumed as appropriate, the categorization, the way of split to train and test sets, the usage of one performance merit, etc., leave a lot to be desired.
- (iii)
- Another study [77] examined the “discrepancies” between AI suggestions and clinicians’ actual decisions on whether the patients should be treated in a spoke- or a hub center. Here, five parameters were considered: accuracy (76%), AUC ROC (83%), specificity (78%), recall (74%), and precision, i.e., positive predicted value (88%). The enigmatic formulation of conclusions—“[the code] is in line or slightly worse than those reported in literature for other AI driven tools” and “may help in selecting patients”—just means the opposite c.f., as shown in ref. [26].
- (iv)
Supplementary Materials
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
Appendix A
- Substantial contributions to the conception or design of the work; or the acquisition, analysis, or interpretation of data for the work.
- Drafting the work or revising it critically for important intellectual content.
- Final approval of the version to be published.
- Agreement to be accountable for all aspects of the work in ensuring that questions related to the accuracy or integrity of any part of the work are appropriately investigated and resolved.
References
- Máttyus Nepomuk, J. Lótudomány Bands I and II; Pytheas Könyvmanufaktúra: Budapest, Hungary, 2008. reprint of 1845 edition. (In Hungarian) [Google Scholar]
- Ardabili, S.-F.; Mosavi, A.; Ghamisi, P.; Ferdinand, F.; Varkonyi-Koczy, A.R.; Reuter, U.; Rabczuk, T.; Atkinson, P.M. COVID-19 Outbreak Prediction with Machine Learning. Algorithms 2020, 13, 249. [Google Scholar] [CrossRef]
- Kuhn, T.S. The Structure of Scientific Revolutions; 50th Anniversary Edition; University of Chicago Press: Chicago, IL, USA, 2012; pp. 1–264. [Google Scholar]
- Occam’s razor. Available online: https://en.wikipedia.org/wiki/Occam%27s_razor (accessed on 29 September 2023).
- Breiman, L. Statistical Modeling: The Two Cultures. Stat. Sci. 2001, 16, 199–231. [Google Scholar] [CrossRef]
- Teter, M.D.; Newman, A.M.; Weiss, M. Consistent notation for presenting complex optimization models in technical writing. Surv. Oper. Res. Manag. Sci. 2016, 21, 1–17. [Google Scholar] [CrossRef]
- Frank, I.E.; Friedman, J.H. A Statistical View of Some Chemometrics Regression Tools. Technometrics 1993, 35, 109–135. [Google Scholar] [CrossRef]
- Gramatica, P. Principles of QSAR Modeling: Comments and Suggestions from Personal Experience. Int. J. Quant. Struct.-Prop. Relat. 2020, 5, 61–97. [Google Scholar] [CrossRef]
- Kirkpatrick, S.; Gelatt, C.D., Jr.; Vecchi, M.P. Optimization by Simulated Annealing. Science 1983, 220, 671–680. [Google Scholar] [CrossRef]
- Glover, F. Future paths for integer programming and links to artificial intelligence. Comp. Oper. Res. 1986, 13, 533–549. [Google Scholar] [CrossRef]
- Holland, J.H. Genetic Algorithms. Sci. Am. 1992, 267, 66–72. [Google Scholar] [CrossRef]
- Kennedy, J.; Eberhart, R. Particle swarm optimization. In Proceedings of the IEEE International Conference on Neural Networks—Conference Proceedings, Perth, WA, Australia, 27 November–1 December 1995; Volume 4, pp. 1942–1948, Code 44687. [Google Scholar]
- Dorigo, M.; Stützle, T. Ant Colony Optimization; MIT Press: Cambridge, MA, USA, 2004; pp. 1–305. [Google Scholar]
- Karaboga, D. An Idea Based on Honey Bee Swarm for Numerical Optimization. In Technical Report-TR06; Department of Computer Engineering, Engineering Faculty, Erciyes University: Kayseri, Türkiye, 2005; Available online: https://www.researchgate.net/publication/255638348 (accessed on 9 January 2024).
- Karaboga, D.; Basturk, B. Artificial Bee Colony (ABC) Optimization Algorithm for Solving Constrained Optimization Problems. In Foundations of Fuzzy Logic and Soft Computing, Proceedings of the International Fuzzy Systems Association World Congress, IFSA 2007, Cancun, Mexico, 18–21 June 2007; Melin, P., Castillo, O., Aguilar, L.T., Kacprzyk, J., Pedrycz, W., Eds.; LNAI 4529; Springer: Berlin/Heidelberg, Germany, 2007; pp. 789–798. Available online: https://link.springer.com/chapter/10.1007/978-3-540-72950-1_77 (accessed on 9 January 2024).
- Yang, X.S. Firefly Algorithm, Chapter 10. In Nature-Inspired Metaheuristic Algorithms; Luniver Press: Bristol, UK, 2008; pp. 81–104. Available online: https://www.researchgate.net/publication/235979455 (accessed on 9 January 2004).
- Yang, X.S.; Deb, S. Cuckoo search via Lévy flights. In Proceedings of the World Congress on Nature & Biologically Inspired Computing (NaBic 2009), Coimbatore, India, 9–11 December 2009; IEEE Publications: New York, NY, USA, 2009; pp. 210–214. [Google Scholar] [CrossRef]
- Gandomi, A.H.; Alavi, A.H. Krill herd: A new bio-inspired optimization algorithm. Commun. Nonlinear Sci. Numer. Simul. 2012, 17, 4831–4845. [Google Scholar] [CrossRef]
- Mirjalili, S.; Mirjalili, S.M.; Lewis, A. Grey Wolf Optimizer. Adv. Eng. Softw. 2014, 69, 46–61. [Google Scholar] [CrossRef]
- Héberger, K. Sum of ranking differences compares methods or models fairly. TRAC—Trends Anal. Chem. 2010, 29, 101–109. [Google Scholar] [CrossRef]
- Kollár-Hunek, K.; Héberger, K. Method and model comparison by sum of ranking differences in cases of repeated observations (ties). Chemom. Intell. Lab. Syst. 2013, 127, 139–146. [Google Scholar] [CrossRef]
- Available online: http://aki.ttk.mta.hu/srd (accessed on 5 October 2023).
- Héberger, K.; Kollár-Hunek, K. Sum of ranking differences for method discrimination and its validation: Comparison of ranks with random numbers. J. Chemom. 2011, 25, 151–158. [Google Scholar] [CrossRef]
- Sziklai, B.R.; Héberger, K. Apportionment and districting by Sum of Ranking Differences. PLoS ONE 2020, 15, e0229209. [Google Scholar] [CrossRef] [PubMed]
- Lourenço, J.M.; Lebensztajn, L. Post-Pareto Optimality Analysis with Sum of Ranking Differences. IEEE Trans. Magn. 2018, 54, 8202810. [Google Scholar] [CrossRef]
- Available online: https://www.orchidenglish.com/british-understatement/ (accessed on 5 October 2023).
- Available online: http://www.icmje.org/recommendations/browse/roles-and-responsibilities/defining-the-role-of-authors-and-contributors.html (accessed on 10 October 2023).
- Ojha, P.K.; Roy, K. Comparative QSARs for antimalarial endochins: Importance of descriptor-thinning and noise reduction prior to feature selection. Chemom. Intell. Lab. Syst. 2011, 109, 146–161. [Google Scholar] [CrossRef]
- Gramatica, P. External Evaluation of QSAR Models, in Addition to Cross-Validation: Verification of Predictive Capability on Totally New Chemicals. Mol. Inf. 2014, 33, 311–314. [Google Scholar] [CrossRef]
- Vincze, A.; Dargó, G.; Rácz, A.; Balogh, G.T. A corneal-PAMPA-based in silico model for predicting corneal permeability. J. Pharm. Biomed. Anal. 2021, 203, 114218. [Google Scholar] [CrossRef]
- Brownlee, J. Overfitting and Underfitting with Machine Learning Algorithms; Machine Learning Mastery: San Juan, Puerto Rico, 2019; Available online: https://machinelearningmastery.com/overfitting-and-underfitting-with-machine-learning-algorithms/ (accessed on 10 October 2023).
- Schwarz, G.E. Estimating the dimension of a model. Ann. Stat. 1978, 6, 461–464. [Google Scholar] [CrossRef]
- Akaike, H. A New Look at the Statistical Model Identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Draper, N.R.; Smith, I.L. Applied Regression Analysis, 2nd ed.; John Wiley & Sons: New York, NY, USA, 1981; Chapter 1; pp. 1–69. ISBN 0471170828. [Google Scholar]
- Rider, P.R. Introduction to Modern Statistical Methods; ASIN: B001UIDASK; John Wiley & Sons: New York, NY, USA, 1939; p. 58. [Google Scholar]
- Bevington, R. Data Reduction and Error Analysis for the Physical Sciences; McGraw-Hill Book Company: New York, NY, USA, 1969; Chapter 7-2, Correlation between many variables; pp. 127–133. [Google Scholar]
- Héberger, K. Discrimination between Linear and Non-Linear Models Describing Retention Data of Alkylbenzenes in Gas-Chromatography. Chromatographia 1990, 29, 375–384. [Google Scholar] [CrossRef]
- Héberger, K. Empirical Correlations Between Gas-Chromatographic Retention Data and Physical or Topological Properties of Solute Molecules. Anal. Chim. Acta 1989, 223, 161–174. [Google Scholar] [CrossRef]
- Bard, Y. Nonlinear Parameter Estimation; Academic Press: New York, NY, USA, 1974; pp. 269–271. [Google Scholar]
- Erichson, N.B.; Zheng, P.; Manohar, K.; Brunton, S.L.; Kutz, J.N.; Aravkin, A.Y. Sparse Principal Component Analysis via Variable Projection. SIAM J. Appl. Math. 2020, 80, 977–1002. [Google Scholar] [CrossRef]
- Todeschini, R.; Consonni, V. Molecular Descriptors for Chemoinformatics; WILEY-VCH Verlag: Weinheim, Germany; GmbH & Co. KGaA: Weinheim, Germany, 2010; Volume 2, pp. 1–252. [Google Scholar] [CrossRef]
- Rácz, A.; Bajusz, D.; Héberger, K. Intercorrelation limits in molecular descriptor preselection for QSAR/QSPR. Mol. Inform. 2019, 38, 1800154. [Google Scholar] [CrossRef] [PubMed]
- García, S.; Luengo, J.; Herrera, F. Tutorial on practical tips of the most influential data preprocessing algorithms in data mining. Knowl.-Based Syst. 2016, 98, 1–29. [Google Scholar] [CrossRef]
- Rücker, C.; Rücker, G.; Meringer, M. y-Randomization and Its Variants in QSPR/QSAR. J. Chem. Inf. Model. 2007, 47, 2345–2357. [Google Scholar] [CrossRef] [PubMed]
- Bro, R.; Kjeldahl, K.; Smilde, A.K.; Kiers, H.A.L. Cross-validation of component models: A critical look at current methods. Anal. Bioanal. Chem. 2008, 390, 1241–1251. [Google Scholar] [CrossRef]
- Using Cross-Validation. Available online: http://wiki.eigenvector.com/index.php?title=Using_Cross-Validation (accessed on 11 November 2023).
- Heberger, K.; Kollar-Hunek, K. Comparison of validation variants by sum of ranking differences and ANOVA. J. Chemom. 2019, 33, e3104. [Google Scholar] [CrossRef]
- Baumann, D.; Baumann, K. Reliable estimation of prediction errors for QSAR models under model uncertainty using double cross-validation. J. Cheminform. 2014, 6, 47. Available online: http://www.jcheminf.com/content/6/1/47 (accessed on 9 January 2024). [CrossRef]
- Filzmoser, P.; Liebmann, B.; Varmuza, K. Repeated double cross validation. J. Chemom. 2009, 23, 160–171. [Google Scholar] [CrossRef]
- Gütlein, M.; Helma, C.; Karwath, A.; Kramer, S. A Large-Scale Empirical Evaluation of Cross-Validation and External Test Set Validation in (Q)SAR. Mol. Inf. 2013, 32, 516–528. [Google Scholar] [CrossRef] [PubMed]
- Rácz, A.; Bajusz, D.; Héberger, K. Consistency of QSAR models: Correct split of training and test sets, ranking of models and performance parameters. SAR QSAR Environ. Res. 2015, 26, 683–700. [Google Scholar] [CrossRef] [PubMed]
- Esbensen, K.H.; Geladi, P. Principles of proper validation: Use and abuse of re-sampling for validation. J. Chemom. 2010, 24, 168–187. [Google Scholar] [CrossRef]
- Miller, A. Part 1.4 ‘Black box’ use of best-subsets techniques. In Subset Selection in Regression; Chapman and Hall: London, UK, 1990; p. 13. [Google Scholar]
- Hastie, T.; Tibshirani, R.; Friedman, J.H. Chapter 7.10 Cross-validation. In The Elements of Statistical Learning: Data Mining, Inference, and Prediction, 2nd ed.; Springer: New York, NY, USA, 2009; pp. 241–249. Available online: https://hastie.su.domains/Papers/ESLII.pdf (accessed on 9 January 2024).
- Kennard, R.W.; Stone, L.A. Computer aided design of experiments. Technometrics 1969, 11, 137–148. [Google Scholar] [CrossRef]
- Rácz, A.; Bajusz, D.; Héberger, K. Effect of Dataset Size and Train/Test Split Ratios in QSAR/QSPR Multiclass Classification. Molecules 2021, 26, 1111. [Google Scholar] [CrossRef] [PubMed]
- Efron, B. Estimating the Error Rate of a Prediction Rule: Improvement of Cross-Validation. J. Am. Stat. Assoc. 1983, 78, 316–331. Available online: https://www.jstor.org/stable/2288636 (accessed on 9 January 2024). [CrossRef]
- Kalivas, J.H.; Forrester, J.B.; Seipel, H.A. QSAR modeling based on the bias/variance compromise: A harmonious and parsimonious approach. J. Comput.-Aided Mol. Des. 2004, 18, 537–547. [Google Scholar] [CrossRef]
- Rácz, A.; Bajusz, D.; Héberger, K. Modelling methods and cross-validation variants in QSAR: A multi-level analysis. SAR QSAR Environ. Res. 2018, 29, 661–674. [Google Scholar] [CrossRef]
- Consonni, V.; Ballabio, D.; Todeschini, R. Evaluation of model predictive ability by external validation techniques. J. Chemom. 2010, 24, 194–201. [Google Scholar] [CrossRef]
- Tóth, G.; Király, P.; Kovács, D. Effect of variable allocation on validation and optimality parameters and on cross-optimization perspectives. Chemom. Intell. Lab. Syst. 2020, 204, 104106. [Google Scholar] [CrossRef]
- Roy, P.P.; Leonard, J.T.; Roy, K. Exploring the impact of size of training sets for the development of predictive QSAR models. Chemom. Intell. Lab. Syst. 2008, 90, 31–42. [Google Scholar] [CrossRef]
- Todeschini, R.; Consonni, V.; Mauri, A.; Pavan, M. Detecting “bad” regression models: Multicriteria fitness functions in regression analysis. Anal. Chim. Acta 2004, 515, 199–208. [Google Scholar] [CrossRef]
- Staněk, F. Optimal out-of-sample forecast evaluation under stationarity. J. Forecast. 2023, 42, 2249–2279. [Google Scholar] [CrossRef]
- Spiliotis, E.; Petropoulos, F.; Assimakopoulos, V. On the Disagreement of Forecasting Model Selection Criteria. Forecasting 2023, 5, 487–498. [Google Scholar] [CrossRef]
- Crichton, M. Jurassic Park; Ballantine Books: New York, NY, USA, 1990; p. 306. [Google Scholar]
- Ortega Hypothesis. Available online: https://en.wikipedia.org/wiki/Ortega_hypothesis (accessed on 14 November 2023).
- Száva-Kováts, E. The false ‘Ortega Hypothesis’: A literature science case study. J. Inform. Sci. 2004, 30, 496–508. [Google Scholar] [CrossRef]
- Aksha, A.; Abedi, M.; Shekarchizadeh, N.; Burkhard, F.C.; Katoch, M.; Bigger-Allen, A.; Adam, R.M.; Monastyrskaya, K.; Gheinani, A.H. MLcps: Machine learning cumulative performance score for classification problems. GigaScience 2023, 12, giad108. [Google Scholar] [CrossRef]
- Kollár-Hunek, K.; Heszberger, J.; Kókai, Z.; Láng-Lázi, M.; Papp, E. Testing panel consistency with GCAP method in food profile analysis. J. Chemometr. 2008, 22, 218–226. [Google Scholar] [CrossRef]
- Di Lascio, E.; Gerebtzoff, G.; Rodríguez-Pérez, R. Systematic Evaluation of Local and Global Machine Learning Models for the Prediction of ADME Properties. Mol. Pharm. 2023, 20, 1758–1767. [Google Scholar] [CrossRef]
- Kalivas, J.H. Overview of two-norm (L2) and one-norm (L1) Tikhonov regularization variants for full wavelength or sparse spectral multivariate calibration models or maintenance. J. Chemometr. 2012, 26, 218–230. [Google Scholar] [CrossRef]
- Belesis, N.D.; Papanastasopoulos, G.A.; Vasilatos, M.A. Predicting the Profitability of Directional Changes using Machine Learning: Evidence from European Countries. J. Risk Financ. Manag. 2023, 16, 520. [Google Scholar] [CrossRef]
- Chen, X.; Cho, Y.H.; Dou, Y.; Lev, B. Predicting Future Earnings Changes using Machine Learning and Detailed Financial Data. J. Account. Res. 2022, 60, 467–515. [Google Scholar] [CrossRef]
- Bhadouria, A.S.; Singh, R.K. Machine learning model for healthcare investments predicting the length of stay in a hospital and mortality rate. Multimed. Tools Appl. 2023. [Google Scholar] [CrossRef]
- Samy, S.S.; Karthick, S.; Ghosal, M.; Singh, S.; Sudarsan, J.S.; Nithiyanantham, S. Adoption of machine learning algorithm for predicting the length of stay of patients (construction workers) during COVID pandemic. Int. J. Inf. Technol. 2023, 15, 2613–2621. [Google Scholar] [CrossRef] [PubMed]
- Catalano, M.; Bortolotto, C.; Nicora, G.; Achilli, M.F.; Consonni, A.; Ruongo, L.; Callea, G.; Tito, A.L.; Biasibetti, C.; Donatelli, A.; et al. Performance of an AI algorithm during the different phases of the COVID pandemics: What can we learn from the AI and vice versa. Eur. J. Radiol. 2023, 11, 100497. [Google Scholar] [CrossRef]
- Pan, N.; Qin, K.; Yu, Y.; Long, Y.; Zhang, X.; He, M.; Suo, X.; Zhang, S.; Sweeney, J.A.; Wang, S.; et al. Pre-COVID brain functional connectome features prospectively predict emergence of distress symptoms after onset of the COVID-19 pandemic. Psychol. Med. 2023, 53, 5155–5166. [Google Scholar] [CrossRef]
- Mehrabi, N.; Morstatter, F.; Saxena, N.; Lerman, K.; Galstyan., A. A Survey on Bias and Fairness in Machine Learning. ACM Comput. Surv. 2021, 54, 115. [Google Scholar] [CrossRef]












| Cluster | Abbreviation | Cluster | Abbreviation |
|---|---|---|---|
| A | Lgs_GWO | B | Pow_PSO |
| A | Cop_GWO | B | Qad_GA |
| A | Exp_GWO | C | Qad_GWO |
| B | Lgs_PSO | C | Cub_PSO |
| B | Lin_GA | C | Cop_PSO |
| B | Lin_PSO | C | Pow_GWO |
| B | Lin_GWO | C | Exp_PSO |
| B | Lgt_GA | D | Lgs_GA |
| B | Lgt_PSO | E | Qad_PSO |
| B | Lgt_GWO | E | Cop_GA |
| B | Cub_GWO | F | Cub_GA |
| B | Pow_GA | F | Exp_GA |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2024 by the author. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Héberger, K. Frequent Errors in Modeling by Machine Learning: A Prototype Case of Predicting the Timely Evolution of COVID-19 Pandemic. Algorithms 2024, 17, 43. https://doi.org/10.3390/a17010043
Héberger K. Frequent Errors in Modeling by Machine Learning: A Prototype Case of Predicting the Timely Evolution of COVID-19 Pandemic. Algorithms. 2024; 17(1):43. https://doi.org/10.3390/a17010043
Chicago/Turabian StyleHéberger, Károly. 2024. "Frequent Errors in Modeling by Machine Learning: A Prototype Case of Predicting the Timely Evolution of COVID-19 Pandemic" Algorithms 17, no. 1: 43. https://doi.org/10.3390/a17010043
APA StyleHéberger, K. (2024). Frequent Errors in Modeling by Machine Learning: A Prototype Case of Predicting the Timely Evolution of COVID-19 Pandemic. Algorithms, 17(1), 43. https://doi.org/10.3390/a17010043