Fast Rescheduling of Multiple Workflows to Constrained Heterogeneous Resources Using Multi-Criteria Memetic Computing

Abstract

This paper is motivated by, but not limited to, the task of scheduling jobs organized in workflows to a computational grid. Due to the dynamic nature of grid computing, more or less permanent replanning is required so that only very limited time is available to come up with a revised plan. To meet the requirements of both users and resource owners, a multi-objective optimization comprising execution time and costs is needed. This paper summarizes our work over the last six years in this field, and reports new results obtained by the combination of heuristics and evolutionary search in an adaptive Memetic Algorithm. We will show how different heuristics contribute to solving varying replanning scenarios and investigate the question of the maximum manageable work load for a grid of growing size starting with a load of 200 jobs and 20 resources up to 7000 jobs and 700 resources. Furthermore, the effect of four different local searchers incorporated into the evolutionary search is studied. We will also report briefly on approaches that failed within the short time frame given for planning.

1. Introduction

A computational grid consists of a mass of heterogeneous resources such as computing nodes, storage devices, application software and their licenses, operating systems, and communication links. All these resources usually differ in size, performance, and costs, and their availability may be restricted to certain hours of the day or days of the week, etc. Furthermore, the prices may differ at different times reflecting that e.g., computer time is cheaper at night or on the weekend. Summarizing, the grid can be characterized as a huge virtualized computing center, the resources of which are requested by grid jobs originated by grid users; cf. [1]. Typically, the task a user wants to be solved by the grid consists of several single grid jobs organized as a workflow, which has the form of a directed acyclic graph. Thus, we will distinguish between elementary grid jobs requesting one or more resources (e.g., the license for a specific software tool, an appropriate operating system, and a suitable hardware to run on) and application jobs representing the workflow of the grid jobs belonging together.

The resulting scheduling problem is of greater complexity than the well-known job-shop scheduling problem due to the following reasons:

• Scheduling of workflows of parallel branches instead of just a linear sequence of operations (grid jobs);
• Co-allocation of resources for each grid job instead of only one machine (resource) per operation;
• Restricted availability of resources;
• Heterogeneous resource alternatives due to different cost performance ratios as well as different performances or capacities instead of alternatives of uniform resources;
• Multi-objective target function with conflicting criteria like costs, execution times, and rate of utilization. This is necessary to fulfill the different needs of resource providers and users.

As the classical job-shop scheduling problem is both, NP-complete and a special case of the outlined task, the grid job scheduling problem is NP-complete as well. Therefore and because of the limited time available for planning, only approximate solutions can be expected. In Section 3, we will give a formal definition of the problem.

A widely used solution to grid job management is the application of queuing systems. As they yield only sub-optimal solutions for nontrivial workloads, we proposed advanced planning and reservation at an early stage, firstly as a concept in 2005 [2] and a year later first results were reported [3]. Planning requires, among other things, knowledge about the expected execution times and information about the performance of the computing nodes. The latter must be standardized to be comparable and is therefore a requirement of the grid information system used. Execution times can be derived either from former executions of the same task with different data, from experience, or must be estimated.

In contrast to many other scheduling problems, a grid job schedule is usually executed to a more or less small extent only. Grid computing is a highly dynamic process, as changes in jobs and resources occur permanently. The following events belong to these replanning inducements:

• Arrival of new application jobs;
• Cancellation of waiting or already begun application jobs;
• Crash of grid jobs resulting in the termination of the remaining workflow;
• New resources;
• Breakdown of resources;
• Changes of the availability or the cost model of resources.

Thus, a permanent replanning process is required. The time for planning should be much shorter than the average of the job execution time. As grid jobs are more likely to last hours rather than seconds, we consider a small time frame of a few minutes to be defensible. Thus, we consider three minutes to be an acceptable amount of time for coming up with a revised plan. Jobs already running or started within this time will not be rescheduled, provided that their resources are still in operation. As changes usually affect a small part of the plan only, it is taken as a base for replanning as described later in Section 4.

Our Global Optimizing Resource Broker and Allocator GORBA performs a heuristic planning, the results of which are used to seed the start population of subsequent evolutionary or memetic optimization. The GORBA concept and the algorithms used are described in Section 4, while the experiments and the benchmarks are explained in Section 5. In this section, we will firstly summaries older results concerning the impact of the Evolutionary Algorithm (EA) and two sets of heuristics. One set is aimed at constructing a new plan from scratch while the other set exploits the old plan. More space is devoted to the investigation of four new local searchers, which serve as memes turning the EA into a Multi-memetic Algorithm. We will compare the results of the pure EA and the different Memetic Algorithms (MA) and investigate to which number of jobs and resources the basic EA and the different MAs can improve the heuristic results.

This paper summarizes the work of the last six years and not all attempts tried out were successful. In Section 6 we will report briefly on failed memetic approaches and on unsuccessful heuristics which have proven to be helpful in other contexts like the well-known Giffler-Thompson algorithm [4] or Tabu search [5]. It must be stressed that most of these failures may be observed only, if the planning time is restricted, and other results may be obtained, if more time was available. Section 7 gives a summary and an outlook.

2. Related Work

When we developed the concept of GORBA, a comparable problem could not be found in the published literature, see e.g., [6,7]. A literature review included in a paper by Setämaa-Kärkkäinen et al. published in 2006 [8] came to a similar result. They found only a few publications that dealt with more than one criterion in scheduling and, if so, they were mostly based on single-machine problems. But after that, more papers dealing with multi-objective optimization were published, especially in the field of grid job computing. In a review article published two years later [9] it is reported that most of them are based on two criteria like e.g., the work of Dutot et al. [10] and that in most cases just one criterion is really optimized while the other serves as a constraint like in [11] or [12]. The latter can handle about 30 jobs within one hour only, which is probably due to the complex chromosomes they used. A true multi-objective optimization based on a modified weighted sum aiming at a compromise between resource owners and users was performed by Kurowski et al. [13]. They used contradicting criteria like costs and several time-related objectives, but their solution did not handle workflows. Two years later, they extended their procedure to hierarchical two-level scheduling and reported about experiments with workloads of about 500 independent jobs [14]. A multi-layer approach is also favored by Tchernykh et al. [15] and they also work with individual jobs, for which the makespan is minimized. Kurowski et al. [16] extended their recent work in 2010 to parallel tasks and the integration of the standard multi-objective genetic algorithm NSGA-II [17]. For that they used advanced reservations of multiple computing nodes. They experimented with 1500 jobs, which were grouped into 60 sets and assigned optimization preferences. Mika et al. [18] schedule workflows instead of single jobs to constrained resources as we do and discuss the analogy with the resource-constrained project scheduling problem (RCPSP), see also [7]. They stress and discuss the similarity of the problem with other application fields and introduce an algorithm for finding feasible solutions.

The approach of Xhafa et al. published in 2008 [19] comes closest to ours, with the following common features: Usage of a Memetic Algorithm, a structured population, the concept of fast and permanent replanning, multi-criteria optimization, and experiments based on workloads and heterogeneous resource pools of up to half the size of ours. The main differences concern the question of what is scheduled, the extent of using heuristics, the number of criteria considered and their contrariness, the MA concept, and the kind of structured population. Our work is based on scheduling multiple workflows of grid jobs, while Xhafa et al. consider independent single jobs only. We use more heuristics for seeding the initial population and for resource allocation, as we have found that heuristic resource selection outperforms its evolutionary counterpart, if the runtime for planning is strictly limited [20]. In [19] two criteria, makespan and average flow time, are used, which can be regarded as less conflicting than time, costs, and utilization rate, which will be explained in more detail in Section 3. In contrast to [19], we use adaptive MAs, as explained in Section 4.4, to steer local search parameters as well as the frequency of local search usage. In [19] this is controlled manually, which is more costly. Furthermore, one of our MAs is an adaptive Multimeme Algorithm, where all local procedures work together and compete for application as will be described later. The last difference concerns population structures and the concept of cellular MAs based on the diffusion model, for which two authors of [19] claim that they are “a new class of algorithms” [21]. Since the early 90’s, our EA has been using a ring-shaped diffusion model, which is described in more detail in Section 4.2.1 [22,23,24]. This also holds for the memetic enhancements of our algorithm starting in 2001 [25]. Cellular Evolutionary Algorithms were already known in the last century, see e.g., [26]. Thus, it is nice to see that diffusion models and the concept of cellular EAs still are of scientific interest. The work of Nguyen et al. on Cellular Memetic Algorithms [27] is another example of the continued attractiveness of one- or two-dimensional diffusion models. The results of Xhafa et al. [19] can be compared with ours only very roughly, as the benchmarks differ not only in workflow or single job scheduling, but also in the frequency of replanning. We investigate one replanning situation in each experiment, while their work is based on frequent replanning situations. Overall, both approaches can be regarded as successful solutions to the problem of fast rescheduling of grid jobs.

3. Formal Problem Definition

For completeness, we will give here a formal definition of the problem, which was already published in [20]. The notation used is common to scheduling literature [6,7] to facilitate comparisons with other scheduling problems. Given are a set M = {M₁, …, M_m} of resources, a set J = {J₁, …, J_r} of r application jobs, and a set O of grid jobs. The n grid jobs of application job J_i are denoted O_i1, …, O_in.. The following functions are given:

• A precedence function p:O × O → {TRUE, FALSE} for the grid jobs;
• An assignment function μ:O → P(P(M)) from grid jobs to resource sets. P(M) is the power set of M, i.e., the set of all possible combinations of resources. Thus, O_ij can be performed by a feasible element from P(M). Then μ_ij ∈ P(P(M)) is the set of all possible combinations of resources from M, which together are able to perform the grid job O_ij;
• A function t:O × P(M) → $\Re$, which gives for every grid job O_ij the time needed for the processing on a resource set R_ij ∈ μ_ij;
• A cost function, c: $\Re$ × P(M) → $\Re$, which gives for every time z ∈ $\Re$ the costs per time unit of the given resource set.

Optimization is done by choosing suitable start times s(Oij) ∈ $\Re$ and resource allocations R_ij ∈ μ_ij. A solution is valid, if the following two restrictions are met:

• All grid jobs are planned and resources are allocated exclusively:

  $$\begin{array}{c}\forall O_{ij}:\exists s(O_{ij})\in \Re ,R_{ij}\in {\mu }_{ij}:\forall M_k\in R_{ij}:\\ M_k\text{ is in [}s(O_{ij});s(O_{ij})+t(O_{ij},R_{ij})\text{] exclusively allocated by }{O}_{ij}.\end{array}$$

  (1)
• Precedence relations are adhered to:

  $$\forall i,j\ne k:p(O_{ij},O_{ik})\Rightarrow s(O_{ik})\ge s(O_{ij})+t(O_{ij},R_{ij})$$

  (2)

A violation of the two following soft constraints is treated by penalty functions as described below.

• All application jobs J_i have a cost limit c_i, which must be observed:

  $$\forall J_i:c_i\ge {\displaystyle \sum _{j=1}^n{\displaystyle \underset{s(O_{ij})}{\overset{s(O_{ij})+t(O_{ij},R_{ij})}{\int }}c(z,R_{ij})dz}}$$

  (3)
• All application jobs J_i have due dates d_i, which must be adhered to:

  $$\forall J_i:d_i\ge s(O_{in})+t(O_{in},R_{in})\text{ where }{Q}_{in}\text{ is the last grid job of }{J}_i$$

  (4)

There are four penalty functions, each of which yields a value of one (no violation) dropping to zero, which stands for maximum overrun. For each constraint, the number of violating application jobs nv and the amount of violation is assessed as pfn and pfa as shown in Equation (5):

$$pfn=\frac{r-nv}{r}\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}pfa=e^{2\cdot \ln (1/3)\cdot (a-1)}\text{\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}\hspace{0.17em}}a=\frac{1}{nv}{\displaystyle \sum _{i=1}^{nv}\frac{va{l}_i}{m_i}}$$

(5)

where r is the total number of application jobs, val_i is the required time or costs of the violating application job i and m_i is its maximum allowed time or costs respectively. The constants of the exponential function yield a value of one third for a = 1.5 which corresponds to an average overrun of 50% of the allowed value m_i.

These penalty values are multiplied by the weighted sum of the following five criteria, thus resulting in the final objective value or fitness as it is called in the context of Evolutionary Algorithms. The first two criteria reflect more the interests of the users, while the criteria 3 and 4 meet more the demands of the resource providers. The fifth criterion is an auxiliary criterion, which helps to reduce the makespan of application jobs. The weights of the five criteria are given in brackets:

• costs of the application jobs (35%)
  are measured with respect to the budget of each application job given by the user and averaged.
• completion time of the application jobs (25%)
  is also measured with respect to a user-given time frame of each application job and averaged.
• total makespan of all application jobs (15%)
• the rate of resource utilization (5%)
  is gathered for the first 75% of the total makespan only, as in the end phase of a schedule not all resources can be utilized.
• delay of inner grid jobs (20%)
  inner grid jobs are all non-terminal grid jobs of an application job. If they start late, there is no or only little room to start the final grid job(s) earlier so that the complete application job is finished earlier, resulting in a better value of the main objective completion time. An earlier start of inner grid jobs is in fact a prerequisite for a faster processing of the application job, but it is not honored by the criteria discussed so far. Thus, the delays of inner grid jobs with respect to the earliest starting time of their application job are measured and averaged over all application jobs. For the costs, no corresponding action is required, as a change in costs caused by the substitution of a resource is registered immediately. This illustrates an important difference for an objective function used in an evolutionary search: It is not sufficient to assess quality differences well. The fitness function must also support the search process in finding the way to better solutions in order to achieve improvements.

For the calculation of the weighted sum, the criteria must be somehow comparable. A further desirable property is that the formula for their calculation is independent of the scheduling task on hand. This is achieved by introducing relative measures where required. As costs and completion time are already calculated as the averaged rate of utilization of a user-given budget or time frame, they are comparable and their calculation method does not depend on the details of a given scheduling task. The same holds for the rate of resource utilization. In the first planning phase of GORBA described in the next section, lower and upper estimations for the processing times of all application jobs are calculated. They serve as a reference for the total makespan. Thus, the makespan can be expressed as rate of utilization of this time frame. As the remaining auxiliary criterion can also be calculated with respect to the given time frame of each application job before averaging, all criteria are calculated as a rate of budget or time frame utilization and are therefore comparable. The values are weighted using the above given weights, summed up, and the result may be reduced by the multiplication by the outcome of the penalty functions, if necessary. The weights are based on experience and aimed at reaching a fair compromise between users and resource providers. The tuning of the suggested adjustment is left to the system administrator.

We use the weighted sum to aggregate the different criteria instead of Pareto optimization, because one solution, and not a set of Pareto-optimal ones, is required in an automated scheduling process. Pareto optimization would require a final selection step using something like weights as well for the different criteria to pick one result as the final solution.

4. The Concept of GORBA for Fast Rescheduling

GORBA executes a two-stage planning process. In the first stage, the actual scheduling task is checked for plausibility firstly. The critical path of each new application job is calculated and it is checked whether there are resources available to process it at all and within the given time and at the given costs. In this way, unrealistic tasks can be identified before the scheduling process itself starts by applying two sets of heuristics. The first set originates from early experiments aimed at the evaluation of the scheduling procedures. The grid is empty and the scheduling task reflects some sort of initial planning situation. The second set utilizes the interrupted plan, also called the old plan. If no allocation conflicts and no violations of restrictions occur, the best heuristic result is regarded as the final outcome and the second stage is dropped.

In the second phase, the Evolutionary Algorithm (EA) described later on is applied using all results from the first stage to seed its initial population. Since we use an elitist EA, the final outcome has the quality of the best heuristic at the minimum. Furthermore, seeding the start population improves the quality of the evolutionary search [20]. The main motivation for the usage of a meta-heuristic like an Evolutionary or Memetic Algorithm is the ability of this algorithm class to come up quickly with a “good” or at least feasible solution. For this area of application, optimality is not a necessary requirement, as schedules are usually processed to a small extent only. A thorough discussion of further reasons can be found in [28].

4.1. Heuristics for Scheduling and Rescheduling

Both sets of heuristics work in two steps. In its first step the first set produces three sequences of grid jobs each based on one of the following three precedence rules:

• earliest due time: grid jobs of the application job with the earliest due time first,
• shortest working time of grid job: grid jobs with the shortest working time first,
• shortest working time of application job: grid jobs of the application job with the shortest working time first.

In the next step resources are allocated to the grid jobs using one of the following three resource allocation strategies (RAS):

RAS-1:

Use the fastest of the earliest available resources for all grid jobs.

RAS-2:

Use the cheapest of the earliest available resources for all grid jobs.

RAS-3:

Use RAS-1 or RAS-2 for all grid jobs of an application job according to its time/cost preference given by the user.

As every RAS is applied to each grid job sequence, nine schedules are generated by the first set.

The second set is aimed at handling the replanning situation. For this the grid jobs of the old plan are divided into two groups: all grid jobs which have been already started or will be started within the planning time, i.e., the next three minutes, belong to the first group. From this group, all grid jobs are extracted which cannot be processed using the previously assigned resources. Together with the rest of the old grid jobs, they form the second group, which is subject to rescheduling. The first group can be regarded as fixed jobs, which are not affected by the rescheduling event.

The grid jobs of the second group are placed in the same sequence as in the old plan. If rescheduling was caused by the arrival of one or more new application jobs, their new grid jobs are sorted according to one of the three heuristic rules already described and added to the sequence of old jobs, yielding three different sequences. Resources are allocated using the three RAS and again, nine more schedules are generated, but this time based on information of the old plan. The best of these eighteen schedules is the final result of the first planning stage, while all are used to seed the subsequent EA run of the second stage. As for other reasons for replanning, there is only the sequence of the old plan to which the three RAS are applied so that there are only twelve heuristic solutions. To sum up, the scheduling sequence of the old plan is still used as far as possible, while the resource allocation may differ especially when the set of resources is changed or new grid jobs are processed.

4.2. Evolutionary Optimization

Evolutionary Algorithms are inspired by the fundamental mechanisms of information processing of natural evolution especially heredity and selection of the fittest. As with nature the scope of application is very wide. Information is coded on some sort of strings comparable to the chromosomes. The algorithmic counterpart of evolution works with a population of solutions called individuals, represented by one chromosome in most cases. Heredity is performed by the selection of two individuals acting as parents. They produce offspring by exchanging information of their chromosomes (crossover) and stochastic changes (mutation). Selection takes place when parents are selected or when the offspring have to compete for survival in the next generation. The latter can be performed among offspring only or among offspring and parents, resulting in an elitist algorithm where the best individual never dies. This is a wanted deviation from the paradigm, as we are interested in optimization rather than permanent adaptation.

The main area of application of EAs covers tasks for which no exact or specialized solutions exist mainly because of their complexity. The most important precondition for EA application is the existence of an evaluation function serving as a fitness measure. It must allow the quantification of quality differences. Another precondition is the amount of time required to assess an individual, as EAs need to process some ten thousands of individuals or more depending on the application on hand. As the start population can be seeded with some already existing solutions for the same or a similar problem, the amount of generations and, hence, time required to come up with a good or at least feasible solution can be shortened. In our case, the solutions of the heuristics described in the previous section can serve as starting points for the evolutionary search. Nevertheless, EAs are known to improve solutions fast in the beginning, but to converge slowly in the end. This issue is discussed in the next section. For more information about EAs and their applications, the interested reader is referred to the following books [29,30,31].

4.2.1. GLEAM

We use the Evolutionary Algorithm GLEAM (General Learning Evolutionary Algorithm and Method), as it has already been applied successfully to other combinatorial problems like the planning of collision-free robot movements [31,32], TSP-like problems [33] or other scheduling tasks [31]. A complete description of GLEAM, its extensions, and its applications can be found in [31]. In contrast to many other EAs, GLEAM allows the aggregation of parameters belonging semantically together in one gene. A gene is the elementary unit of a chromosome, which may be shifted within the chromosome or the parameters of which may be altered by the corresponding mutation operators. This allows an easy and flexible mapping of the problem parameters to the genes of the chromosome, which is called gene model within the context of GLEAM. Furthermore, there is an evolvable meta-structure for each chromosome, called segmentation. The lower part of Figure 1 shows an example of a segmented chromosome of simple genes without parameters representing grid jobs and one more complex gene with one parameter, the RAS-gene. The details of this example are explained later. The segments serve as the basis for some macro mutations suited among others for combinatorial optimization:

• inversion: reversion of the internal order of the genes of a segment.
• segment shifting: a segment is shifted as a whole.
• segment merging: if non-adjacent segments are merged, the operation includes segment shifting.
• segment mutation: all genes of a segment undergo parameter mutation with a given probability.

Figure 1. Example of a segmented chromosome organized as a linear list. It is based on gene model GM2. It represents a legal schedule of the two workflows above as explained in the text. The position of the RAS gene is arbitrary and of no importance. In the lower right corner an example of a gene of GM1 representing a grid job needing three resources is given.

Figure 1. Example of a segmented chromosome organized as a linear list. It is based on gene model GM2. It represents a legal schedule of the two workflows above as explained in the text. The position of the RAS gene is arbitrary and of no importance. In the lower right corner an example of a gene of GM1 representing a grid job needing three resources is given.

Segment boundaries are also used as crossover points for the standard 1- and n-point crossover operators, which include a genetic repair that ensures that every offspring does not lack genes in the end. Thus, segments can only be passed to the offspring as a whole. The idea behind this concept is to allow the establishment of meaningful building blocks of partial solutions, which are inherited.

Instead of the frequently used panmictic population, which is characterized by the ability of each individual to choose any other individual as a partner, the population of GLEAM is based on a diffusion model of overlapping local neighborhoods [22]. The individuals are located on a ring implying a geographical neighborhood with the individuals on both sides. Partner selection and offspring acceptance take place only within the neighborhoods. Figure 2 shows an example of small neighborhoods, also called demes, with a size of four neighbors. Since demes overlap, as shown in Figure 1, genotypic information can spread. As this spreading is much slower than with panmictic populations, niches of more or less similar individuals can emerge, develop, disperse, meet each other, and compete. Thus, genotypic diversity is preserved over a longer period of time. Furthermore, neighborhood models like this one cause an adaptive balance between exploration and exploitation resulting in faster, more robust runs compared to their panmictic counterpart [22,34,35].

Figure 2. Diffusion model based on overlapping neighborhoods, called demes. The demes of the two individuals “M” and “N” show minimal overlapping, while “X” and “Y” overlap maximally.

Figure 2. Diffusion model based on overlapping neighborhoods, called demes. The demes of the two individuals “M” and “N” show minimal overlapping, while “X” and “Y” overlap maximally.

4.2.2. Two Gene Models

For GORBA, two different gene models were investigated in detail. For both, each grid job is represented by one gene and the sequence of genes within the chromosome determines the scheduling sequence. A grid job gene consists of at least a unique grid job identifier (id in Figure 1). The first gene model GM1 is based on genes that determine each resource of a grid job by a corresponding gene parameter. This means that every grid job gene has as many parameters as resources have to be allocated or co-allocated. Figure 1 shows an example of such a gene marked by a light blue background. A schedule is constructed from a chromosome by performing the following steps for each gene in the order of their appearance:

• If the grid job has no predecessors, its earliest start time equals the earliest start time of its application job. Otherwise, the latest end time of its predecessors is used as earliest start time.
• Calculate the duration of the grid job on the given resources.
• Search for a free time interval of the calculated duration beginning at the earliest start time from step 1 on all selected resources and allocate them.

This gene model covers the complete search space, as every scheduling sequence and every resource assignment is possible. Both are controlled by evolution.

The second gene model GM2 is aimed at a faster improvement in the beginning of the search by a reasonable reduction of the search space. It replaces the evolutionary selection of resources per grid job by the evolutionary selection of one of the three RAS heuristics, which is applied to all grid jobs. This is done by the removal of the parameters of the grid job genes and an additional RAS gene. Figure 1 shows this RAS gene, which is interpreted first independently of its position within the chromosome. The crossover operators are modified to pass on the RAS gene of the better parent. For chromosome interpretation, the first step of GM1 is used again:

• If the grid job has no predecessors, its earliest start time equals the earliest start time of its application job. Otherwise, the latest end time of its predecessors is used as earliest start time.
• According to the RAS selected by the RAS gene, a list of alternatives is produced for every primary resource.
• Beginning with the first resources of the lists, the duration of the job is calculated and it is searched for a free time slot for the primary resource and its depending ones, beginning at the earliest start time of step 1. If no suitable slot is found, the resources at the next position of the lists are tried.
• The resources found are allocated to the grid job with the calculated time frame.

This scheduling mechanism ensures that the precedence rules are adhered to for chromosomes, which contain no gene representing a direct predecessor of a grid job O_ij, which is located after the gene of that grid job. Alternatively, a repair is performed as described in the next section. An example of the relationship between chromosomes and workflows is shown in Figure 1. The rationale of this reduction of the search space is as follows: Due to the limited time frame, evolutionary search is stopped (long) before convergence anyway, provided that the amount of grid jobs is large enough, i.e., 100 grid jobs or more. This means that any attempt to approach the global optimum is in vain and that it is therefore meaningful to increase fitness improvement in an early stage of the search at the costs of lower achievable quality in the long run. Figure 3 illustrates this idea. In fact, results from early experiments confirm this assumption [36].

Figure 3. Basic course of evolution for both gene models for about 100 grid jobs and more.

Figure 3. Basic course of evolution for both gene models for about 100 grid jobs and more.

4.2.3. Genotypic and Phenotypic Repair

The interpretation of the chromosomes described ensures that the precedence relations of grid jobs are not violated as long as no gene is located before the gene of its preceding grid job. As this may be interfered with by some genetic operators, two alternative repair mechanisms were implemented and assessed: the genetic repair searches for all genes of grid jobs, the genes of the preceding grid jobs of which are not located on the chromosome before. Such a gene is shifted until all genes of preceding grid jobs are on prior positions. As an unwanted result, the mechanism may hamper meaningful steps of shifting genes. Phenotypic repair is aimed at a correct interpretation of a chromosome rather than altering it. If the processing of a gene tries to schedule a grid job with missing already scheduled predecessors, it simply suspends the scheduling until all predecessors will have been scheduled. The advantage of this approach is that there are no faulty schedules and that intermediate steps of shifting genes, which itself may be faulty, are now allowed to occur and hopefully result in a better schedule. Earlier experiments confirmed this expectation [20,36].

4.2.4. Crossover Operators Designed for Combinatorial Optimization

Two crossover operators from literature, which are aimed at passing on sequence information, were tested: The well-known order-based crossover OX [28,37] preserves the relative order of the parent genes, while the precedence-preserving operator PPX [38] does this more strictly by perpetuating the absolute order. In contrast to OX, PPX ensures that sequence-correct parents produce sequence-correct offspring at the price of limited gene mixing. The results showed a clear superiority of the OX operator for the GORBA application, if it is used in addition to the standard 1- and n-point crossover operators [20]. Thus, all further investigations are based on GM2 in conjunction with phenotypic repair and the order-based crossover.

4.3. Memetic Optimization

Hybridizations of an Evolutionary Algorithm with one or more heuristics or local searchers are known to perform significantly better than each algorithm alone [37]. Two forms of hybridization are used frequently: The seeding of the start population with heuristic results as already applied and the incorporation of heuristic improvement in the process of offspring creation. The latter type is also called Memetic Algorithm (MA), a term coined by Moscato [39]. Figure 3 shows the pseudo code of a standard EA (light grey) with its memetic extension marked by a dark grey background. In Figure 4 the heuristic or local searcher, called meme, improves either all or the best offspring of a mating. Based on suited heuristics or local searchers (LS), MAs have been applied successfully to such different domains as continuous, mixed-integer, or combinatorial optimization or combinations thereof [37,40,41,42]. An up-to-date survey on Memetic Computing can be found in [43]. The advantage of a performance increased by factors of ten and more is compensated by the disadvantage that the choice of suited memes is crucial to success and that additional strategy parameters are introduced. These strategy parameters control the intensity of local search, the frequency of meme application, and the selection of offspring to be treated by a meme, see [44,45]. In Figure 4, most of these parameters are hard coded like the search intensity of the meme by an iteration limit or by a termination threshold. The frequency of meme application is simply set to each pairing while the offspring selection can be steered by the parameter all_improvement to some extent. Both disadvantages mentioned above can be overcome by an adaptive parameter control and meme selection as described for example in [24,40,41]. Of course, good candidates for a set of memes must still be chosen manually and the adaptation figures out, which are better in which stage of the evolutionary process. Another question which must be answered when an EA is expanded to an MA is whether the solution found by the meme should be coded back to the chromosome (Lamarckian evolution) or not (Baldwin evolution). The observed disadvantage of Lamarckian evolution is the danger of premature convergence of the population [46,47]. As we use the diffusion model described above, which already promotes genotypic diversity by niching, we found Lamarckian evolution to perform better than its Baldwinian counterpart [40,48]. Thus, Figure 4 contains the code for the chromosome update of an accepted and improved offspring.

For scheduling, it is not so easy to define suitable local searchers as for other combinatorial problems. For example, for the well-known Travelling Salesman Problem, it is easy to decide whether a small change of the tour is beneficial or not without recalculating the complete tour. In contrast to that, a small change like the selection of a different resource or the swap of the sequence of two grid jobs cannot be judged without setting up the complete allocation matrix. Thus, the usage of local searchers is more costly for a scheduling application in general and for the GORBA problem in particular than for many other combinatorial tasks. The experiments will show whether the price of evaluations paid to assess the results of local search justifies their benefit of improving solutions found so far by the evolution.

Figure 4. Pseudo code of a simple Memetic Algorithm. The memetic part is indicated by a dark grey background. The decision on the acceptance of the best offspring of a mating is, of course, also performed in pure EA. In GLEAM (General Learning Evolutionary Algorithm and Method) an accepted offspring replaces its parent.

Figure 4. Pseudo code of a simple Memetic Algorithm. The memetic part is indicated by a dark grey background. The decision on the acceptance of the best offspring of a mating is, of course, also performed in pure EA. In GLEAM (General Learning Evolutionary Algorithm and Method) an accepted offspring replaces its parent.

We suggest and compare four different local searchers: Three are aimed at finding a better grid job sequence by shifting the grid jobs of too late application jobs to the left (i.e., start them earlier) in two different ways or by shifting the grid jobs of application jobs with a large time reserve to the right (i.e., start them later). All shifts are done such that no precedence violations occur. These three LS are inspired by the gap reduction approach used e.g., in [49] and the consideration of the critical path, see e.g., [50]. The fourth local searcher tries to tackle both, time and costs, by altering the RAS based on the results of the actual schedule and the RAS used. They are described in the next sections.

4.3.1. Local Searchers for Left Shift of Grid Jobs of Late Application Jobs (LS-LSLD and LS-LSSD)

As a first step, the number of delayed application jobs is determined and a fraction α₁ between 2% and 100% of them is selected. The first version of the left shift takes the α₁ fraction of most delayed application jobs, while the second one works on the α₁ less delayed. The first approach reflects the idea to tackle the biggest problems at first and is abbreviated by LSLD (left shift of large delays). The second procedure is aimed at the presumably easier cases of delay in order to get more application jobs processed in time. It is denoted by LSSD (left shift of small delays). If there are no late application jobs, the local searcher works accordingly on the application jobs with the smallest time reserve.

For each grid job of a selected application job, the amount of time it should start earlier for meeting the due date of its application job is determined. This amount is varied by multiplying it by a second strategy parameter α₂, which takes values between 0.85 and 1.2. The idea is to allow shifts, which are slightly larger or smaller than computed, because the calculation is based on the actual application job only and cannot take the effect of all the other application jobs into account, with which it competes in resource allocation. Consequently, the calculated shifting usually is a rough figure only.

For each of the two local searchers, we have two strategy parameters α₁ and α₂, which are controlled adaptively as described in Section 4.4.

4.3.2. Local Searcher Right Shift of Grid Jobs of Preterm Application Jobs (LS-RS)

When considering the shifting of grid jobs, either delayed jobs can be started earlier or jobs with a considerable time reserve may start later and, thus, give room to other jobs to begin earlier. The idea is that many of these earlier started jobs would be late otherwise. For the selection of the application jobs to undergo local search, the maximum time reserve is calculated. A fraction of β% (50 ≤ β ≤ 100) of this reserve is used as a threshold value, and every application job with a time reserve of this value at the minimum is selected. This means that for β = 100 only the application jobs with the largest time reserve are selected. The strategy parameter β is also controlled adaptively as described in Section 4.4. Again, the amount of shifting is done with respect to the processing times and due dates. The procedure is denoted by RS (right shift) in the figures below.

4.3.3. Local Searcher RAS Selection (LS-RAS)

The selection of the RAS used is changed by this LS according to the conformity of the schedule with the time and cost constraints of the application jobs. The following four situations are possible. Besides overrun-free application jobs, there may be jobs with cost or time or both overruns. Depending on the situation, alternative RAS are tried according to Table 1 and the following rules. If both overrun situations are given, both rules of Table 1 are applied. If no overrun occurs, the two remaining RAS are checked in each case. This LS has no strategy parameters.

Table 1. RAS alternatives depending on two overrun situations of the actual schedule. The abbreviation fastest means the usage of the fastest of the earliest available resource (RAS-1), cheapest the same with the cheapest of the earliest available resource (RAS-2), and preference means RAS-3, where RAS-1 or RAS-2 is selected according to a user-given preference of the application job.

Overrun	Actual RAS
	Cheapest	Fastest	Preference
cost	preference	cheapest, preference	cheapest
time	fastest, preference	preference	fastest

Table 1. RAS alternatives depending on two overrun situations of the actual schedule. The abbreviation fastest means the usage of the fastest of the earliest available resource (RAS-1), cheapest the same with the cheapest of the earliest available resource (RAS-2), and preference means RAS-3, where RAS-1 or RAS-2 is selected according to a user-given preference of the application job.

Overrun	Actual RAS
	Cheapest	Fastest	Preference
cost	preference	cheapest, preference	cheapest
time	fastest, preference	preference	fastest

4.4. Adaptive Memetic Algorithms

The less strategy parameters an algorithm needs to be adjusted, the fewer mistakes can be made and the less experience of the user is required. This is why adaptivity was added to MAs at an early stage [40,41,51,52] and the research in this field is still going on, see e.g., [53]. In our memetic extension of GLEAM, called HyGLEAM (Hybrid General Purpose Evolutionary Algorithm and Method) [24,25,31,40,48], three types of MAs are included besides the basic algorithms:

• The simple Memetic Algorithm, where one meme is used without any adaptivity, see also Figure 4,
• The Adaptive Single-memetic Algorithm (ASMA) consisting of one meme, the application of which is adjusted adaptively, and
• The Adaptive Multimeme Algorithm (AMMA), where both, meme selection and their application are controlled adaptively.

The adaptation is based on costs measured in additional evaluations caused by the meme and on the benefit of local search measured as relative fitness gain rfg as given in (6), where f_LS is the fitness obtained from the local searcher LS applied to the offspring with the fitness f_evo. Fitness values are normalized in the range of 0 and f_max, which turns every task into a maximization problem. f_max can be regarded an upper estimation of the fitness.

$$rfg=\{\begin{array}{l}\frac{f_{LS}-f_{evo}}{f_{\max }-f_{evo}}\\ 0\end{array}\begin{array}{l}\text{if }{f}_{LS}>f_{evo}\\ \text{else}\end{array}$$

(6)

In case of multiple memes, an initially equal selection probability is assigned to every meme. These probabilities p_i are adjusted from time to time according to Equation (7).

$$p_i=\frac{\text{1}}{{\displaystyle \sum _{i=\text{1}}^n\frac{rfg(L{S}_i)}{eval(L{S}_i)}}}\cdot \frac{rfg(L{S}_i)}{eval(L{S}_i)}$$

(7)

where n is the number of local searches (LS), rfg(LS_i) is the sum of the relative fitness gains of a particular LS_i, and eval(LS_i) is the sum of evaluations needed to achieve these fitness improvements, both recorded since the last adjustment. The same approach is used to tune strategy parameters of memes by selecting one out of a given set. This cost-benefit-based adaptation procedure is described in detail in [24].

Thus, the only remaining strategy parameter of the MA is the choice between the LS application to the best or all offspring per pairing, called best- and all-improvement. For both adaptive algorithms, there is an adaptive variant of the all-improvement, which always applies the LS to the best offspring of a mating, while its siblings are treated with an adaptively controlled likeliness. Hence, it is left to adaptation how many offspring are locally improved according to the benefit gained and the additional costs induced. Figure 5 shows the pseudo code of the AMMA with the adaptive memetic part indicated by a dark grey background. The Boolean strategy parameter all_improvement distinguishes between best- and adaptive all-improvement. The adaptations of the probabilities for meme selection, strategy parameters of a meme, and for adjustment of p_all are indicated in the color blue.

In contrast to many other local searchers, the application of all shifting LS introduced requires one additional evaluation each regardless of their strategy parameters and the LS-RAS may require two. Thus, for the application on hand, the adaptation is based mainly on the benefit obtained from a certain parameter setting.

In the experiments, we compare the solutions found by pure GLEAM, the AMMA based on all four memes, and two ASMAs using the two best performing memes found in the AMMA runs. For both MA types the strategy parameters of the three shifting LS are set adaptively, while the choice between best-improvement and adaptive all-improvement is controlled manually.

Figure 5. Pseudo code of the Adaptive Multimeme Algorithm AMMA. The adaptive memetic part is marked by a dark grey background. For details of the EA part see Figure 4.

Figure 5. Pseudo code of the Adaptive Multimeme Algorithm AMMA. The adaptive memetic part is marked by a dark grey background. For details of the EA part see Figure 4.

5. Experiments

In this section, we will firstly introduce the benchmarks used in Section 5.1 before the experimental results are given in Section 5.2.

5.1. Benchmarks

Benchmarks for the assessment of scheduling procedures can either be derived from real applications or generated synthetically. Practical relevance seems to be an argument in favor of the first approach, but benchmarks extracted from real data tend to inherit those application scenarios which were dominant during data collection or which were typical of a given user domain [13,54]. Additionally, characteristic properties are difficult to control and consequently, we use synthetic benchmarks. Examples are given in [55,56], who use homogeneous resources and only one application job. As we consider a more general application with heterogeneous resources and many workflows, we started early to develop our own benchmark set as described in [57]. The complexity of a benchmark certainly depends on its size, i.e., the number of grid and application jobs as well as the number of resources. Besides these more general figures, the degree of mutual dependencies of the grid jobs D and the degree of freedom in the selection of resources R are used to characterize a benchmark more precisely. D is defined as follows.

$$D=\frac{{\displaystyle \sum _{i=1}^{n}pre{d}_i}}{pre{d}_{\max }}pre{d}_{\max }=\frac{n(n-1)}{2}$$

(8)

where n is the number of all grid jobs of all application jobs and pred_i is the number of all direct or indirect predecessors of grid job i.

The degree of resource alternatives R is given by Equation (9).

$$R=\frac{{\displaystyle \sum _{i=1}^n{m}_i}}{n\cdot m}$$

(9)

where m is the number of all usable resources and m_i is the number of all alternatively usable resources of grid job i. A small value of R corresponds to a small mean possibility of selection of resources per grid job.

By using small (s) and large (l) values for R and D, four benchmark classes are defined, which are labeled sRsD, sRlD, lRsD, and lRlD. They range from a low degree of resource alternatives and parallelization (sRlD) to many resource alternatives and a high level of parallelization (lRsD). For these four classes, benchmarks are constructed for given values of n and m.

The complexity of the planning problem also depends on user requirements for the application jobs like cost budgets and latest completion times. An approach to measuring these properties will be presented in the next paragraph. For the first experiments, we used the attribute “free of budget violations and processed in time” to distinguish between a successful and an unsuccessful schedule. This differentiation was applied as an additional measure besides the fitness introduced in Section 3 to compare the schedulers. For this purpose, these two constraints of a benchmark were adjusted in such a way that the heuristics for the first planning phase just could not solve them although it was possible. All scheduling algorithms and their settings are assessed in the experiments by the achieved success rate as described before and the resulting fitness.

For the second benchmark set used for the new experiments reported in Section 5.2.3, further measurands were introduced for the time and cost constraints in order to ensure their homogeneity when varying the loads. The time and cost reserve of an application job are calculated based on the usage of average fast and expensive resources, the critical path of the workflow, and on the average off-time of resources, as described in detail in [58]. They are given as percentages of the corresponding time frame and budget. Of course, these figures are based on an “empty grid”, i.e., there are no delays due to other jobs or there is no need to use e.g., more expensive resources in order to meet the due date. The time and cost reserves t_res and c_res are summed up for all application jobs of a benchmark and averaged to $\overline{t_{res,bm}}$ and $\overline{c_{res,bm}}$ per benchmark bm, called time and cost benchmark reserve. For the experiments regarding the manageable load, 23 benchmarks with grid job numbers between 200 and 7000 were constructed per class, which are processed by a likewise increasing number of resources starting with 20 and ending with 700. For the benchmarks of a class, the two reserves per benchmark are to change as little as possible with varying size. Table 2 shows the mean values of the benchmark reserves per benchmark class $\overline{t_{res}}$ and $\overline{c_{res}}$ together with the minima and maxima of $\overline{t_{res,bm}}$ and $\overline{c_{res,bm}}$. The table shows that the values per benchmark class deviate within a small range only. Thus, we can conclude that the benchmarks of a class differ mostly in size and not in the two key properties budget and time reserves. Furthermore, the small differences between the classes reflect the flexibility for scheduling given by the R and D values and the goal of budgets and time frames so tight that the basic heuristics for initial planning cannot solve them without violations.

Table 2. Averages $\overline{t_{res}}$ and $\overline{c_{res}}$ of the time and cost benchmark reserves $\overline{t_{res,bm}}$ and $\overline{c_{res,bm}}$ together with their minima and maxima per benchmark class, see also [58]. The reserve values are given as percentages of the corresponding budgets and time frames.

Benchmark class	Time benchmark reserve (%)			Cost benchmark reserve (%)
	$\mathbf{min}(\overline{{\mathit{t}}_{\mathit{r}\mathit{e}\mathit{s},\mathit{b}\mathit{m}}})$	$\overline{{\mathit{t}}_{\mathit{r}\mathit{e}\mathit{s}}}$	$\mathbf{max}(\overline{{\mathit{t}}_{\mathit{r}\mathit{e}\mathit{s},\mathit{b}\mathit{m}}})$	$\mathbf{min}(\overline{{\mathit{c}}_{\mathit{r}\mathit{e}\mathit{s},\mathit{b}\mathit{m}}})$	$\overline{{\mathit{c}}_{\mathit{r}\mathit{e}\mathit{s}}}$	$\mathbf{max}(\overline{{\mathit{c}}_{\mathit{r}\mathit{e}\mathit{s}.\mathit{b}\mathit{m}}})$
lRlD	47.2	48.9	50.1	27.3	27.7	28.1
sRlD	53.7	55.9	58.3	25.2	25.9	26.7
lRsD	57.2	59.2	62.1	22.3	23.3	24.1
sRsD	63.4	64.4	65.5	20.8	21.5	22.0

Table 2. Averages $\overline{t_{res}}$ and $\overline{c_{res}}$ of the time and cost benchmark reserves $\overline{t_{res,bm}}$ and $\overline{c_{res,bm}}$ together with their minima and maxima per benchmark class, see also [58]. The reserve values are given as percentages of the corresponding budgets and time frames.

Benchmark class	Time benchmark reserve (%)			Cost benchmark reserve (%)
	$\mathbf{min}(\overline{{\mathit{t}}_{\mathit{r}\mathit{e}\mathit{s},\mathit{b}\mathit{m}}})$	$\overline{{\mathit{t}}_{\mathit{r}\mathit{e}\mathit{s}}}$	$\mathbf{max}(\overline{{\mathit{t}}_{\mathit{r}\mathit{e}\mathit{s},\mathit{b}\mathit{m}}})$	$\mathbf{min}(\overline{{\mathit{c}}_{\mathit{r}\mathit{e}\mathit{s},\mathit{b}\mathit{m}}})$	$\overline{{\mathit{c}}_{\mathit{r}\mathit{e}\mathit{s}}}$	$\mathbf{max}(\overline{{\mathit{c}}_{\mathit{r}\mathit{e}\mathit{s}.\mathit{b}\mathit{m}}})$
lRlD	47.2	48.9	50.1	27.3	27.7	28.1
sRlD	53.7	55.9	58.3	25.2	25.9	26.7
lRsD	57.2	59.2	62.1	22.3	23.3	24.1
sRsD	63.4	64.4	65.5	20.8	21.5	22.0

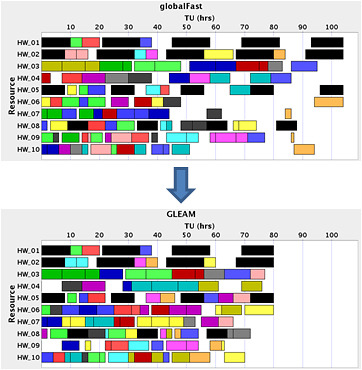
5.2. Experimental Results

As EAs are stochastic procedures, their outcome can only be compared by averages based on a set of runs instead of a single run as with deterministic methods like the heuristics of the first planning phase. Thus, we performed 100 runs for every benchmark setting and population size in the experiments reported in Section 5.2.1. Later on, 50 runs were carried out in the experiments reported here in order to reduce the effort. Every set of runs yields two assessment values as introduced in Section 5.1, the success rate and the averaged fitness gain compared to the best heuristic result. Confidence intervals and t-tests were used to check the significance of differences at a confidence range of at least 95%, where necessary.

For the experiments reported in the next two subsections, population sizes varying from 70 to 600 were tried. This amount was somewhat reduced for MA runs and more drastically with increasing benchmark loads. The outcome of the best performing population size was taken as result of a measurement. For the adaptive MA runs, another strategy parameter was taken into account, the choice between best-improvement and adaptive all-improvement as explained in Section 4.4.

5.2.1. Summary of the Results of Earlier Experiments

As already mentioned above when explaining the two gene models and details of GLEAM and its operators, we found the second gene model in conjunction with phenotypic repair, the usage of the OX crossover as an additional crossover operator, and the fifth auxiliary criterion to be the best choice. These results are based on all four benchmark classes using 50, 100, and 200 grid jobs at 10 resources and 200 grid jobs at 20 resources [20,36]. The effect of seeding the initial population was also investigated and it was found that it improves the results significantly [20]. In the same paper the results of the three heuristics for grid job sequencing were compared using the three RAS each. The earliest due time heuristic yields by far the best results independently of the RAS used. As the other two heuristics are also successful in some cases and their calculation requires only little time, they are still used for seeding the start population. Another reason of their continued use is their relatively high fitness values before the penalty functions are applied. The idea is that their results may serve as good starting material for the evolutionary search.

Based on the results for planning from scratch summarized in the last paragraph, the replanning task was tackled by the investigation of 32 replanning scenarios with varying fractions of finished grid jobs, which were replaced by new ones [59,60]. The most important results are:

• The usage of the old plan as described in Section 4.1 is beneficial especially for small amounts of 10 or 20% finished and new grid jobs.
• Both sets of heuristics introduced in Section 4.1 contribute well, complement each other and GLEAM.
• It is clearly situation-dependent which heuristic or GLEAM performs best.

5.2.2. Assessment of the Processable Workload

In 2010, we published two papers addressing the issue of the processable workload for replanning. In the first publication, this topic was investigated for pure GLEAM and the two benchmark classes based on large dependencies [59]. In the second paper, this investigation was extended to cover the other two benchmark classes and two new sizes (5000 and 7000 grid jobs) [60], but unfortunately, the newly generated benchmarks were faulty due to a software error. For this reason and because of the introduction of the two new benchmark parameters, we generated a complete new set of benchmarks for all four classes based on the rescheduling situation of 10% finished grid jobs and a set of new grid jobs of the same size. The basic scheduling task of each benchmark class consisting of 200 grid jobs and 20 resources was constructed with homogeneous tight budgets and time frames as described in Section 5.1. The basic tasks were scaled up to 7000 grid jobs and 700 resources in steps shown in Figure 6. This resulted in 23 sizes per benchmark class, totaling 92 single benchmarks. To obtain replanning benchmarks, every benchmark was firstly processed by GORBA using the heuristics and GLEAM and its execution was started. Then, the described replanning event occurred, resulting in a rescheduling task as described in detail in [58]. These tasks served as benchmarks for the comparison of GLEAM and the MA variants. For each benchmark, seven measurement series were done to compare the basic EA GLEAM and the following MA variants: The AMMA based on all four local searchers and the two ASMAs using the two best performing local searches from the AMMA runs. Together with the manually controlled choice between best- and adaptive all-improvement (see Section 4.4.), this resulted in six MA variants. Thus, the investigation reported here is based on the total of 644 single measurements. Each of them is performed with different population sizes and the best run is the result of the measurement.

Figure 6. Success rates and fitness gains compared to the best heuristic result for all benchmarks and the basic EA GLEAM. The fitness gains are given with their confidence intervals. In some cases, these intervals are so small that they merge with their marks. The scale was reduced in the lower diagram for a better visibility.

Figure 6. Success rates and fitness gains compared to the best heuristic result for all benchmarks and the basic EA GLEAM. The fitness gains are given with their confidence intervals. In some cases, these intervals are so small that they merge with their marks. The scale was reduced in the lower diagram for a better visibility.

Firstly, the results of the GLEAM runs are presented. Figure 6 shows the success rates and fitness improvements for all 92 benchmarks. The large variations of the improvement rates correspond to weak and good heuristic solutions. The better the heuristics of the first planning phase solve the rescheduling task, the smaller is the room for a subsequent improvement. A detailed analysis of the sources of the final fitness values, which is given in [58], shows that the heuristics and GLEAM complement each other well: weak heuristic results are cured by the subsequent GLEAM run and good heuristic outcomes receive a comparably small improvement only.

The best heuristic solution for the lRlD-200-benchmark is an exception in so far, as the investigated replanning task meets the budget and time constraints, although its basic new planning solution did not. Therefore, an improvement of only 11.6% was achieved. The large improvements in the range of more than 1000% result from poor heuristic replanning solutions, e.g., the normalized fitness of the sRlD-200-benchmark was improved from a value of 2.35 to 61.0, a growth of 2496%. Figure 6 also shows that runs with a success rate of 100% show little deviations in the fitness and, hence, have small confidence intervals. All fitness gains are a significant improvement of the best heuristic results (99.9% confidence). Another question is the further course of the improvement rate beyond the scale of budget and time frame violation-free runs, i.e., for more than 2200 grid jobs. The lower diagram of Figure 6 shows that the improvement rates decrease with increasing load as expected. However, improvements in the range of 33% to 133% achieved for the two largest loads are still worth the additional EA run, especially as these runs reduce the amount of application jobs violating constraints.

5.2.3. Assessment of the Time and Cost Benchmark Reserves

Success rates drop differently with increasing grid job loads depending on the benchmark class, as shown in Figure 6. This reduction is not as continuous within each benchmark class as was expected from the homogeneous values of the time and cost benchmark reserves $\overline{t_{res}}$ and $\overline{c_{res}}$ introduced in Section 5.1. Consequently, it must be concluded that they either do not represent the scheduling difficulty as expected due to the idealized assumption of an empty grid used for their calculation, or that the stochastic elements of the benchmark construction have a greater impact than assumed. The stochastic aspects come from the GLEAM run yielding the initial schedule, which is interrupted by the rescheduling event as described above. The already mentioned variations of the improvement rate per benchmark class during the course of increasing loads correspond to different fitness compensations obtained from the heuristics and GLEAM. This means that the rescheduling benchmarks differ more than intended due to the stochastic elements of their creation. Thus, the reason for the observed inhomogeneous decline of the success rate is mainly considered to lie in stochastic variations of the rescheduling benchmarks rather than in a lack of significance of the cost and time benchmark reserves [58].

5.2.4. Comparison of the Four Local Searchers

As mentioned above, the AMMA controls among others the rate of application of each local searcher or meme by adaptively adjusting its probability to be chosen for application. This includes that poor performing LS may be switched off completely. Figure 7 shows the distribution of averaged LS probabilities recorded at the end of each AMMA run. The dominance of the LS-RS is striking and it corresponds to the findings reported in [49]. The LS-RAS shows a nice performance especially for the all-improvement case. It must be borne in mind that the LS-RAS frequently requires two evaluations and, hence, has to yield often twice the improvement rate of the other LS to be competitive.

Figure 7. Averaged final LS probabilities for all benchmark classes. For a better visibility, the sequence of best- and all-improvement (cf. Section 4.4) is inverted for LS-RAS. The values of each row sum up to 100% for each improvement type. The front row shows the mean of the four benchmark classes. The coloring of the benchmarks and the sum will be maintained in the subsequent Figure 9 and Figure 10, while their sequence is changed for a better visibility of the columns.

Figure 7. Averaged final LS probabilities for all benchmark classes. For a better visibility, the sequence of best- and all-improvement (cf. Section 4.4) is inverted for LS-RAS. The values of each row sum up to 100% for each improvement type. The front row shows the mean of the four benchmark classes. The coloring of the benchmarks and the sum will be maintained in the subsequent Figure 9 and Figure 10, while their sequence is changed for a better visibility of the columns.

The poor results of the two left shifting LS are explained as follows. Shifting the grid jobs of some application jobs means to schedule them either earlier than before (left shift) or later (right shift). In both cases, the removed grid jobs cause a gap in the schedule, which is filled up by other grid jobs starting earlier now, and an insertion of the moved grid jobs. Both are disturbances in the previous structure of the schedule, but their extents vary as shown in Figure 8. In case of a left shift, there is an insertion, which pushes some grid jobs of the insertion area to the right, i.e., they are scheduled later. This may be compensated to some extent by the gap area of the schedule. Hence, the main area of alteration is located left of the gap area. The right shift again produces a gap causing an earlier scheduling until the insertion area is reached, where the shifted grid jobs will frequently find space to fit in. In this case, the area of alteration is right of the gap and occurs later in the scheduling sequence. Therefore, the disturbance induced by a right shift can be assumed to be smaller than by a left shift. We think that this has an impact when applied to the pre-optimized part of the old schedule included in the seeds with which the replanning run was started. It will also have an impact on descendants of these seeds. As an analysis of the seeds shows that some results of the replanning heuristics frequently are of better quality than the other seeds, we can assume that the larger disturbance of the left shift is responsible for its weaker performance. Some experimental runs with an ASMA using the two left shifting LS suggest that this may be the case, but further experiments are required to confirm this.

Figure 8. Different types of disturbances of the original scheduling sequence when shifting grid jobs to the left and to the right.

Figure 8. Different types of disturbances of the original scheduling sequence when shifting grid jobs to the left and to the right.

5.2.5. Comparison of Pure GLEAM, AMMA, and the ASMAs Using the Two Best Performing Memes

Due to the dominance of LS-RS and the good results of LS-RAS, we decided to investigate these two memes in ASMA variants in more detail. In Figure 9, both the success rates and fitness values are averaged for the seven algorithms and all loads between 200 and 2200 grid jobs. This range was chosen, because no successful runs at all were recorded for larger loads. As shown by the diagrams, no large differences can be observed. Although the ASMA-RS shows good results, it is questionable whether the differences are significant and large enough to conclude its superiority.

Figure 9. Averaged success rates and the means of the relative fitness values for all seven algorithms and four benchmark classes in the range of 200 to 2200 grid jobs. The best results per benchmark class are marked by a dotted fill patterns.

Figure 9. Averaged success rates and the means of the relative fitness values for all seven algorithms and four benchmark classes in the range of 200 to 2200 grid jobs. The best results per benchmark class are marked by a dotted fill patterns.

This gives rise to the question regarding the amount of significantly best runs compared to the 2nd best one. The left part of Figure 10 shows the best runs for best-improvement per benchmark class and summed up for all classes. The results of all four algorithms sum up to 87, as the best runs for the five missing benchmarks were achieved using all-improvement. If we restrict to significantly best runs only, 31 runs of 92 possible ones remain. This means that any of the compared four algorithms can be used in about two thirds of the benchmarks. For the remaining third, the choice of algorithm matters, and the distribution of the 30 cases based on best-improvement among algorithms and benchmark classes is shown in the right part of Figure 10. The figure shows that it is benchmark-dependent whether the basic EA, the AMMA, or the ASMA-RS yields the best results and that GLEAM performs best about as often as the two MA variants together. It is also obvious that ASMA-RAS does not perform significantly better than the others in any case. Again, the ASMA based on gap reduction by a right shift turns out to be the best MA variant, which confirms the results of Hasan et al. [49].

Figure 10. Best runs for GLEAM and the three MA variants using best-improvement on the left. The right diagram only shows those runs, which are significantly superior (95% confidence or more).

Figure 10. Best runs for GLEAM and the three MA variants using best-improvement on the left. The right diagram only shows those runs, which are significantly superior (95% confidence or more).

It should be recalled that all results are based on runs, which were prematurely aborted after three minutes. However, it is our intention to improve a fast scheduling and our work is directed towards this goal. If more planning time is available, different results may be obtained for GLEAM and the MA variants.

5.2.6. Processible Workload Revisited

The number of evaluations that can be calculated within the three minutes is shown in Figure 11 for GLEAM, all benchmark classes, and an increasing load. The figures for the MA variants are similar and therefore not reported here. For the two benchmark classes based on a small degree of resource alternatives, more evaluations can be processed, as the resource selection process is faster than for those cases with many alternatives. For more than 5000 grid jobs and 500 resources, the amount of trials to the search space drops below 5000. As it is known for EAs and MAs that an application-dependent number of at least some thousand evaluations is required, we can assume that no further improvements beyond a load of seven or eight thousand grid jobs and 700 or 800 resources are possible with the given hardware and implementation. Below this margin, the additional effort of an EA or MA run based on the heuristic planning is worthwhile.

Figure 11. Evaluation of the best GLEAM runs per benchmark class and with increasing load.

Figure 11. Evaluation of the best GLEAM runs per benchmark class and with increasing load.

6. Failed Approaches

As shown above, the grid job scheduling problem is very complex and it is hard to find good solutions in general and within a limited time frame in particular. Some approaches were tested, which did not work as expected. There are always some failures on the way to a success story and we believe that they should not be omitted. Therefore, they will be reported briefly here and the interested reader is referred to given literature.

6.1. Failed Heuristics for the First Planning Phase

We assessed scheduling heuristics from a literature survey and selected the first five of the following list as most promising candidates to improve the first heuristic planning phase: The Giffler-Thompson algorithm [4,61], List Scheduling [62], Shifting Bottleneck [63,64], Tabu Search [65], Greedy Randomized Adaptive Search Procedure (GRASP) [66], Branch & Bound, Lagrange Relaxation, neural networks, and Simulated Annealing. As described in [20,67], they were adapted to the task at hand, if necessary. The best performing was the Giffler-Thompson procedure, which was able to solve one of the benchmarks better than our simple heuristics at least. However, to our surprise, its results were not suited well as seeds for the start population of GLEAM [20]. The four others were also tested for both outperforming the simple heuristics or yielding good seeds. However, again, there was no success [67].

6.2. Failed Memetic Approaches

Up to this work, all our approaches to using a Memetic Algorithm did not perform better than the pure EA, mainly because we used too much elaborated local searchers like ant colony optimization [68]. It may be concluded that for this task with its limited time for planning, fast memes are required to successfully support the evolutionary search.

Another gene model was tried as well. It substitutes the determination of the grid job sequence according to the gene sequence of the chromosome by a permutation of this sequence. This is achieved by shifting the interpretation sequence of the genes based on an additional integer parameter per gene. Thus, the combinatorial problem is reduced to an optimization task of integers, so that the basic memes of HyGLEAM [24,40] can be used. As the results were clearly inferior to GM1 and GM2, this approach was not pursued any further.

Hahnenkamp reported on some simple gene translocation memes, which produced nice results that were only slightly inferior to pure GLEAM [68]. They were based on shifting, contracting or expanding the gene sequence of the grid jobs of an application job. The results motivated us to develop the four memes introduced in this paper.

7. Conclusion and Outlook

We introduced the task of fast scheduling of multiple workflows of elementary grid jobs to the heterogeneous resources of a computational grid based on multiple objectives and gave a formal definition of the problem. As the classical job-shop scheduling problem is a special case of our more general task, the latter is also NP-complete. The introduced approach is based on a two-stage optimization process beginning with heuristics, the results of which are used as seeds for an additional run of an Evolutionary or Memetic Algorithm (MA). We briefly reported about former assessments of different gene models, two repair strategies and crossover operators, and about the benefit of seeding the start population. The task was extended from the more artificial “planning from scratch scenario” to the practical “replanning situation”. It was reported that the used heuristics and the basic Evolutionary Algorithm (EA) GLEAM complement each other depending on the replanning scenario.

The main contribution of this paper consists in a detailed investigation of the introduced memes and their application in adaptive single-memetic and multimeme algorithms as well as of the maximal processible workload in the context of fast scheduling. Especially the question whether local search based on the assessment of the complete allocation matrix instead of a faster “local assessment” (see the TSP example in Section 4.3) can improve the results within the given short time frame or not, was of interest. And it is also a nice result that the best local searcher found by Hasan et al. [49] also performed well in the context of our scheduling task and under different run time conditions.

For schedules that meet due dates and budgets, the experiments showed that loads of up to 1200 grid jobs and 120 resources can be handled depending on the benchmark scenarios. For schedules that entail at least a betterment compared to the best heuristic results, improvements in the range of 33% to 133% of the heuristic fitness were observed for loads between 6000 and 7000 grid jobs and 600 and 700 resources, respectively. It must be stressed that all these results are based on a planning time of three minutes, which means that the evolutionary search is stopped (long) before convergence. It can be assumed that faster hardware or tuned software will improve the presented results.

Four newly developed local searchers were introduced and assessed in detail. The results displayed in Figure 10 show that, for the scope of the experiments performed, it depends on the particular benchmark which algorithm performs better, the basic EA GLEAM or the two adaptive MA variants using either all local searchers (AMMA) or just the local searcher based on right shift (ASMA-RS). In other words, it depends on the present state of the grid, the existing load, and the type of the replanning event, which algorithm with which parameterization will perform best or at least well in the second planning stage, see also [14]. This is our motivation for the development of a meta-optimizer, which learns from the replanning runs which optimization algorithms and memes are suited best under which conditions, see e.g., [69]. For this purpose, more characteristic figures describing the grid state as well as the load are required to steer meta-optimization. This will be the subject of our future work.