Estimation of Aboveground Oil Palm Biomass in a Mature Plantation in the Congo Basin
Abstract
:1. Introduction
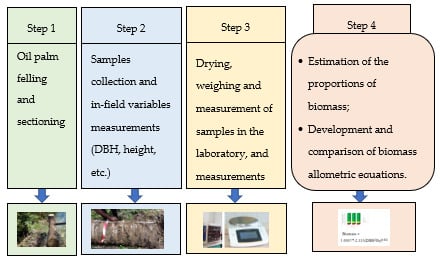
2. Materials and Methods
2.1. Study Area
2.2. Data Collection
2.2.1. Field Data Measurement
2.2.2. Laboratory Measurements
2.3. Establishment and Validation Allometric Models
2.4. Comparisons with Existing Biomass Allometric Models
3. Results
3.1. Distribution of Biomass Proportions
3.2. Relationships between Variables
3.3. Allometric Biomass Models That Were Developed
3.4. Validation of Local Allometric Models
3.5. Validation of Existing Allometric Biomass Models
4. Discussion
4.1. Interpretation of Biomass Distribution
4.2. Evaluation of Local Allometric Biomass Equations
4.3. Comparison of Local Models to Existing Allometric Biomass Models
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Plot Number | BF (Total Fresh Aboveground Biomass of Oil Palm) (kg) | DBH (Diameter at Breast Height, 1.3 m) (cm) | HTOT (Total Height) (m) | HT (Stem Height) (m) | NF (Number of Leaves Per Palm) | DMF (Dry Mass Fraction) Stem Mean | Dmf (Mean Dry Mass Fraction) Of Oil Palm | ρ (Mean Infra-Density of Oil Palm Stem) (g·cm−3) | BRachis (Dry Rachis Biomass) (kg) | BFSR (Dry leaf Biomass without Rachis) (kg) | BLeaf (Dry Leaf Biomass of Oil Palm: Petioles, Fruits, Rachises and Leaflets) (kg) | BStem (Dry Stem Biomass of Oil Palm) (kg) | B (Total Dry Aboveground Biomass (kg) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| 1 | 1336.80 | 50.9 | 16.3 | 8.0 | 32 | 0.2914 | 0.2857 | 0.2819 | 59.8752 | 52.9108 | 112.786 | 269.1137 | 381.8997 |
| 2 | 1643.30 | 53.6 | 16.7 | 9.1 | 36 | 0.3085 | 0.2818 | 0.2921 | 63.0907 | 70.4268 | 133.5175 | 329.4937 | 463.0112 |
| 3 | 1950.20 | 57.6 | 16.4 | 10.0 | 38 | 0.3081 | 0.2853 | 0.3279 | 66.9161 | 70.0291 | 136.9452 | 419.4599 | 556.4051 |
| 4 | 1176.95 | 49.2 | 15.0 | 7.4 | 30 | 0.3105 | 0.2836 | 0.2587 | 50.7830 | 53.1305 | 103.9135 | 229.9270 | 333.8405 |
| 5 | 1259.35 | 49.6 | 15.3 | 7.8 | 30 | 0.3314 | 0.2832 | 0.2872 | 43.1878 | 59.7505 | 102.9383 | 253.6564 | 356.5947 |
| 6 | 1227.44 | 50.4 | 15.3 | 7.5 | 29 | 0.3008 | 0.2902 | 0.2993 | 42.3007 | 36.6779 | 78.9786 | 277.2167 | 356.1953 |
| 7 | 1462.40 | 53.7 | 16.5 | 8.8 | 37 | 0.3365 | 0.2846 | 0.2917 | 55.4954 | 63.7667 | 119.2621 | 296.9790 | 416.2411 |
| 8 | 1623.30 | 55.3 | 16.2 | 8.5 | 34 | 0.3343 | 0.2855 | 0.2972 | 69.4109 | 67.4892 | 136.9001 | 326.5954 | 463.4955 |
| 9 | 1710.05 | 54.9 | 16.1 | 8.5 | 39 | 0.3471 | 0.2843 | 0.3077 | 74.2342 | 74.5585 | 148.7927 | 337.3431 | 486.1358 |
| 10 | 1294.15 | 51.3 | 15.5 | 8.5 | 31 | 0.2972 | 0.2901 | 0.2927 | 55.4954 | 46.9775 | 102.4729 | 272.9780 | 375.4509 |
| 11 | 1763,1 | 55.9 | 18.2 | 9.5 | 38 | 0.3115 | 0.2869 | 0.3180 | 83.1600 | 63.0959 | 146.2559 | 359.6233 | 505.8792 |
| 12 | 1803.75 | 57.9 | 16.6 | 9.8 | 38 | 0.3099 | 0.2862 | 0.3030 | 45.6964 | 68.9378 | 114,6342 | 401,5572 | 516.1914 |
| 13 | 1156.25 | 50.7 | 15.3 | 8.1 | 27 | 0.2987 | 0.2852 | 0.2749 | 29.3832 | 47.7701 | 77.1533 | 252,6299 | 329.7832 |
| 14 | 1672.25 | 57.4 | 17.0 | 8.5 | 37 | 0.2857 | 0.2814 | 0.3260 | 62.5918 | 74.5959 | 137.1877 | 333.4184 | 470.6061 |
| 15 | 1543.70 | 55.4 | 16.6 | 9.5 | 32 | 0.2536 | 0.2889 | 0.2935 | 65.1420 | 52.9177 | 118.0597 | 327.9238 | 445.9835 |
| 16 | 1216.85 | 51.1 | 15.0 | 7.4 | 28 | 0.2650 | 0.2822 | 0.2776 | 41.2474 | 51.4161 | 92.6635 | 250.6978 | 343.3613 |
| 17 | 1021.80 | 48.8 | 14.5 | 6.65 | 30 | 0.2706 | 0.2826 | 0.2500 | 40.8038 | 48.7180 | 89.5218 | 199.1936 | 288.7154 |
| 18 | 1493.20 | 52.0 | 15.1 | 8.8 | 33 | 0.2727 | 0.2871 | 0.2950 | 68.2466 | 48.4361 | 116.6827 | 311.9835 | 428.6662 |
References
- Food and Agriculture Organization. Évaluation des Ressources Forestières Mondiales 2015: Comment les Forêts de la Planète Changent-Elles? 2nd ed.; FAO: Rome, Italy, 2016; pp. 30–31. Available online: http://www.fao.org/3/a-i4793f.pdf (accessed on 28 April 2018).
- Keenan, R.J.; Reams, G.A.; Achard, F.; de Freitas, J.V.; Grainger, A.; Lindquist, R. Dynamics of global forest area: Results from the FAO Global Forest Resources Assessment 2015. For. Ecol. Manag. 2015, 352, 9–20. [Google Scholar] [CrossRef]
- Tuma, J.; Fleiss, S.; Eggleton, P.; Frouz, J.; Klimes, P.; Lewis, O.T.; Yusah, K.M.; Fayle, T.M. Logging of rainforest and conversion to oil palm reduces bioturbator diversity but not levels of bioturbation. Appl. Soil Ecol. 2019, 144, 123–133. [Google Scholar] [CrossRef]
- Khalid, H.; Zin, Z.Z.; Anderson, J.M. Quantification of oil palm biomass and nutrient value in a mature plantation. I, Above-ground biomass. J. Oil Palm Res. 1999, 11, 23–32. Available online: http://jopr.mpob.gov.my/wp-content/uploads/2013/07/joprv11n1-p31.pdf (accessed on 20 October 2018).
- Folefack, A.J.J.; Ngo Njiki, G.M.; Darr, D. Safeguarding forests from smallholder oil palm expansion by more intensive production? The case of Ngwei forest (Cameroon). For. Policy Econ. 2019, 101, 45–61. [Google Scholar] [CrossRef]
- Olorunfemi, I.E.; Komolafe, A.A.; Fasinmirin, J.T.; Olufayo, A.A. Biomass carbon stocks of different land use management in the forest vegetative zone of Nigeria. Acta Oecol. 2019, 95, 45–56. [Google Scholar] [CrossRef]
- Megevand, C.; Mosnier, A.; Hourticq, J.; Sanders, K.; Doetinchem, N.; Streck, C. Deforestation Trends in the Congo Basin: Reconciling Economic Growth and Forest Protection; The World Bank, Directions in Development—Environment and Sustainable Development: Washington, DC, USA, 2013; pp. 4–118. [Google Scholar] [CrossRef] [Green Version]
- Glinskis, E.A.; Gutiérrez-Vélez, V.H. Quantifying and understanding land cover changes by large and small oil palm expansion regimes in the Peruvian Amazon. Land Use Policy 2019, 80, 95–106. [Google Scholar] [CrossRef]
- De Almeida, A.S.; Vieira, I.C.G.; Ferraz, S.F.B. Long-term assessment of oil palm expansion and landscape change in the eastern Brazilian Amazon. Land Use Policy 2020, 90, 104321. [Google Scholar] [CrossRef]
- Rivera, Y.D.; Moreno, A.L.; Romero, H.M. Biochemical and physiological characterization of oil palm interspecific hybrids (Elaeis oleifera x Elaeis guineensis) grown in hydroponics. Acta Biol. Colomb. 2013, 18, 465–472. Available online: https://www.researchgate.net/publication/257938174 (accessed on 11 January 2020).
- Meléndez, M.R.; Ponce, W.P. Pollination in the oil palms Elaeis guineensis, E. oleifera and their hybrids (OxG), in tropical America. Pesqui. Agropecu. Trop. 2016, 46, 102–110. [Google Scholar] [CrossRef] [Green Version]
- Pacheco-Palencia, L.A.; Mertens-Talcott, S. Chemical composition, antioxidant properties, and thermal stability of a phytochemical enriched oil from Acai (Euterpe oleracea Mart.). J. Agric. Food Chem. 2008, 56, 4631–4636. [Google Scholar] [CrossRef]
- Morel, A.C.; Fisher, J.B.; Malhi, Y. Evaluating the potential to monitor aboveground biomass in forest and oil palm in Sabah, Malaysia, for 2000–2008 with Landsat ETM+ and ALOSPALSAR. Int. J. Remote Sens. 2012, 33, 3614–3639. [Google Scholar] [CrossRef]
- Kho, L.-K.; Rudbeck Jepsen, M. Carbon stock of oil palm plantations and tropical forests in Malaysia: A review. Singap. J. Trop. Geogr. 2015, 36, 249–266. [Google Scholar] [CrossRef]
- Lahteenoja, O.; Ruokolainen, K.; Schulman, L.; Oinonen, M. Amazonian peatlands: An ignored C sink and potential source. Glob. Change Biol. 2009, 15, 2311–2320. [Google Scholar] [CrossRef]
- Neumann, M.; Moreno, A.; Mues, V.; Härkönen, S.; Mura, M.; Bouriaud, O.; Lang, M.; Achten, W.M.J.; Thivolle-Cazat, A.; Bronisz, K.; et al. Comparison of carbon estimation methods for European forests. For. Ecol. Manag. 2016, 361, 397–420. [Google Scholar] [CrossRef]
- Tinker, P.B.H.; Smilde, K.W. Dry-matter production and nutrient content of plantation oil palms in Nigeria. II. Nutrient Content. Plant. Soil 1963, 19, 350–363. Available online: https://www.jstor.org/stable/42933246 (accessed on 15 May 2018). [CrossRef]
- Saldarriaga, J.G.; West, D.C.; Tharp, M.L.; Uhl, C. Long-term chronosequence of forest succession in the upper Rio Negro of Colombia and Venezuela. J. Ecol. 1988, 76, 938–958. [Google Scholar] [CrossRef]
- Yuen, J.Q.; Fung, T.; Ziegler, A.D. Review of allometric equations for major land covers in SE Asia: Uncertainty and implications for above- and below-ground carbon estimates. For. Ecol. Manag. 2016, 360, 323–340. [Google Scholar] [CrossRef]
- Thenkabail, P.S.; Stucky, N.; Griscom, B.W.; Ashton, M.S.; Diels, J.; van der Meer, B.; Enclona, E. Biomass estimations and carbon stock calculations in the oil palm plantations of African derived savannas using IKONOS data. Int. J. Remote 2004, 25, 5447–5472. [Google Scholar] [CrossRef]
- Corley, R.H.V.; Tinker, P.B.H. The Oil Palm, 4th ed.; Blackwell Science: Hoboken, NJ, USA, 2003; pp. 89–103. [Google Scholar]
- Da Silva, F.; Suwa, R.; Kajimoto, T.; Ishizuka, M.; Higuchi, N.; Kunert, N. Allometric equations for estimating biomass of Euterpe precatoria, the most abundant palm species in the Amazon. Forests 2015, 6, 450–463. [Google Scholar] [CrossRef] [Green Version]
- Kotowska, M.M.; Leuschner, C.; Triadiati, T.; Meriem, S.; Hertel, D. Quantifying above- and belowground biomass carbon loss with forest conversion in tropical lowlands of Sumatra (Indonesia). Glob. Change Biol. 2015, 21, 3620–3634. [Google Scholar] [CrossRef]
- Aholoukpè, H.; Dubos, B.; Flori, A.; Deleporte, P.; Amadji, G.; Chotte, J.L.; Blavet, D. Estimating aboveground biomass of oil palm: Allometric equations for estimating frond biomass. For. Ecol. Manag. 2013, 292, 122–129. [Google Scholar] [CrossRef]
- Hughes, R.F.; Kauffman, J.B.; Jaramillo, V.J. Biomass, carbon, and nutrient dynamics of secondary forests in a humid tropical region of Mexico. Ecology 1999, 80, 1892–1907. [Google Scholar] [CrossRef]
- Cole, T.G.; Ewel, J.J. Allometric equations for four valuable tropical tree species. For. Ecol. Manag. 2006, 229, 351–360. [Google Scholar] [CrossRef]
- Goodman, R.C.; Phillips, O.L.; Del Castillo Torres, D.; Freitas, L.; Cortese, S.T.; Monteagudo, A.; Baker, T.R. Amazon palm biomass and allometry. For. Ecol. Manag. 2013, 310, 994–1004. [Google Scholar] [CrossRef]
- Moraes, R.M.; Borchsenius, F.; Blicher-Mathiesen, U. Notes on the biology and uses of the Motacú palm (Attalea phalerata, Arecaceae) from Bolivia. Econ. Bot. 1996, 50, 423–428. Available online: www.jstor.org/stable/4255886 (accessed on 10 January 2020).
- Sunaryathy, P.-I.; Suhasman Kanniah, K.-D.; Tan, K.-P. Estimating aboveground biomass of oil palm trees by using the destructive method. World J. Agric. Res. 2015, 3, 17–19. [Google Scholar] [CrossRef]
- Yang, X.; Blagodatsky, S.; Liu, F.; Beckschäfer, P.; Xu, J.; Cadisch, G. Rubber tree allometry, biomass partitioning and carbon stocks in mountainous landscapes of sub-tropical China. For. Ecol. Manag. 2017, 404, 84–99. [Google Scholar] [CrossRef]
- Rondeux, J. La Mesure des Arbres et des Peuplements Forestiers, 2nd ed.; Les Presses Agronomiques de Gembloux: Gembloux, Belgium, 1999; pp. 97–108. [Google Scholar]
- Bauwens, S.; Fayolle, A. Protocole de Collecte des Données sur le Terrain et au Laboratoire Nécessaires pour Quantifier la Biomasse Aérienne des Arbres et pour l’établissement d’équations Allométriques. Nature + 2014, 40. [Google Scholar] [CrossRef]
- Gould, S.J. AlIometry and size in ontogeny and phylogeny. Biol. Rev. 1966, 41, 587–640. [Google Scholar] [CrossRef]
- Brown, S.; Gillespie, A.J.R.; Lugo, A.E. Biomass estimation methods for tropical forests with applications to forest inventory data. For. Sci. 1989, 35, 881–902. [Google Scholar] [CrossRef]
- Onyekwelu, J.-C. Above-ground biomass production and biomass equations for even-aged Gmelina arborea (ROXB) plantations in southwestern Nigeria. Biomass Bioenerg. 2004, 26, 39–46. [Google Scholar] [CrossRef]
- Chave, J.; Andalo, C.; Brown, S.; Cairns, M.A.; Chambers, J.Q.; Eamus, D.; Fölster, H.; Fromard, F.; Higuchi, N.; Kira, T.; et al. Tree allometry and improved estimation of carbon stocks and balance in tropical forests. Oecologia 2005, 145, 87–99. [Google Scholar] [CrossRef] [PubMed]
- Ngomanda, A.; Engone Obiang, L.N.; Lebamba, J.; Moundounga Mavouroulou, Q.; Gomat, H.; Mankou, G.S.; Loumeto, J.; Midoko Iponga, D.; Kossi Ditsouga, F.; Zinga Koumba, R.; et al. Site-specific versus pantropical allometric equations: Which option to estimate the biomass of a moist central African forest? For. Ecol. Manag. 2014, 312, 1–9. [Google Scholar] [CrossRef]
- Hansen, E.H.; Gobakken, T.; Bollandsås, O.M.; Zahabu, E.; Næsset, E. Modeling aboveground biomass in dense tropical submontane rainforest using airborne laser scanner data. Remote Sens. 2015, 7, 788–807. [Google Scholar] [CrossRef] [Green Version]
- Kuyah, S.; Dietz, J.; Muthuri, C.; Jamnadass, R.; Mwangi, P.; Coe, R.; Neufeldt, H. Allometric equations for estimating biomass in agricultural landscapes: I. Aboveground biomass. Agric. Ecosyst. Environ. 2012, 158, 216–224. [Google Scholar] [CrossRef]
- Supriadi, A.; Rachman, O.; Sarwono, E. Characteristics and sawing properties of oil-palm (Elaeis guineensis Jacq.) wood logs. Buletin Penelitian Hasil Hutan 1999, 17, 1–20. [Google Scholar] [CrossRef]







| Parameter | Minimum | Maximum | Mean | SE | %SE |
|---|---|---|---|---|---|
| DBH | 48.8 | 57.9 | 53.1 | 0.71 | 1.34 |
| HT | 6.65 | 10.0 | 8.46 | 0.22 | 2.60 |
| HTOT | 14.5 | 18.2 | 15.97 | 0.22 | 1.38 |
| NF | 27 | 39 | 33.27 | 0.92 | 2.77 |
| Components | Minimum | Maximum | Mean | SE | % SE |
|---|---|---|---|---|---|
| Descriptive Statistical Parameters for Dry Mass Fractions (DMF) | |||||
| Stem | 0.253 | 0.347 | 0.301 | 0.006 | 2.020 |
| Petiole | 0.134 | 0.245 | 0.194 | 0.007 | 3.805 |
| Fruit | 0.156 | 0.221 | 0.190 | 0.009 | 5.059 |
| Rachis | 0.233 | 0.335 | 0.277 | 0.006 | 2.386 |
| Leaflet | 0.198 | 0.386 | 0.322 | 0.010 | 3.215 |
| Whole oil palm | 0.281 | 0.290 | 0.285 | 6.10−4 | 0.220 |
| Descriptive Statistical Parameters for Infra-Density (g·cm−3) | |||||
| Stem | 0.25 | 0.3279 | 0.2930 | 0.0048 | 1.639 |
| Descriptive Statistical Parameters for Total Dry Mass of Oil Palm Compartments (kg) | |||||
| Stem | 199.19 | 419.46 | 302.77 | 13.66 | 4.51 |
| Petiole | 20.89 | 46.31 | 33.28 | 1.64 | 4.92 |
| Fruit | 14 | 82.5 | 58.57 | 10.54 | 17,99 |
| Rachis | 29.38 | 83.16 | 56.50 | 3.31 | 5.86 |
| Leaflet | 13.29 | 29.57 | 21.42 | 1.03 | 4.83 |
| Leaf (Petioles, Fruit, Rachis + Leaflets) | 77.15 | 148.79 | 114.93 | 5.19 | 4.52 |
| Stem + Leaf | 288.72 | 556.41 | 417.69 | 17.78 | 4.26 |
| Source | Geographic Region | Palm Species | Existing Biomass Model (kg tree−1) | CF | r2 | n |
|---|---|---|---|---|---|---|
| Khalid et al. [4] | Malaysia | Elaeis guineensis | BF = 725 + 197 × HTOT | 0.96 | 7 | |
| Thenkabail et al. [20] | Benin | Elaeis guineensis | BF = 1.5729 × HTcm – 8.2835 | 0,97 | 7 | |
| B = 0.3747 × HTcm + 3.6334 | 0.98 | 7 | ||||
| Hughes et al. [25] | Mexico | Astrocaryum mexicanum | B = exp(3.6272 + 0.5768 × ln(DBH2HT)) CF/106 | 1.02 | 0.73 | 15 |
| Saldarriaga et al. [18] | Colombia and Venezuela | Common | B = exp(−6.3789 – 0.877 × ln(1/DBH2) + 2.151 × ln(HT)) | 0.89 | 19 | |
| Goodman et al. [27] | Amazonia (Peru) | Common | B = 0.0950 × (DMF × DBH2HT) | 0.99 | 106 | |
| Da Silva et al. [22] | Brazil | Euterpe precatoria | B = 0.167 × (DBH2HTρ) 0.883 | 0.98 1 | 20 | |
| BStem = exp(0.1212 + 0.90 × ln(DBH2HTρ)) | 0.98 1 | 20 | ||||
| BLeaf = exp(0.0065 + 0.69 × ln(DBH2HTNF)) | 0.94 1 | 20 | ||||
| Cole and Ewel [26] | Tropical zone (Costa Rica) | Euterpe oleraceae | BStem = 0.0314 × (DBH2HT)0.917 × CF | 1.04 | 0.95 | 156 |
| BFSR = 0.0237 × (DBH2HTNF)0.512 × CF | 1.036 | 0.94 | 182 | |||
| BRachis = 0.0458 × (DBH2HTNF)0.388 × CF | 1.036 | 0.90 | 187 |
| Model | a | b | r2 | σ | AIC | CF | p | ER | %ER | RMSE | %RMSE |
|---|---|---|---|---|---|---|---|---|---|---|---|
| Model 1: ln(ρ) = a + b × ln(DBH) | −5.057 | 0.967 | 0.674 | 0.037 | −73.343 | 1.0006 | 0.002 | 75 × 10−5 | 0.075 | 0.034 | 2.793 |
| Model 2: ln(NF) = a + b × ln(DBH) | −3.892 | 1.868 | 0.804 | 0.051 | −63.390 | 1.0011 | 0.0001 | 17.5 × 10−5 | 0.017 | 0.046 | 1.327 |
| Model 3: ln(HT) = a + b × ln(DBH) | −4.342 | 1.608 | 0.806 | 0.044 | −66.843 | 1.0008 | 0.0001 | 34.6 × 10−5 | 0.034 | 0.039 | 1.869 |
| Model 4: ln(HTOT) = a + b × ln(DBH) | −0.179 | 0.746 | 0.538 | 0.038 | −69.769 | 1.0006 | 0.010 | 15.4 × 10−5 | 0.015 | 0.034 | 1.258 |
| Model | a | b | r2 | σ | AIC | P | CF | ER | %ER | RMSE | %RMSE | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Allometric Equations Using Infra-Density (ρ) or DBH as the Predictor | ||||||||||||
| Model 5 | ln(B) = a + bln(ρ) | 8.755 | 2.223 | 0.685 | 0.099 | −48.985 | 0.002 | 1.0041 | 22.1 × 10−5 | 0.022 | 0.089 | 1.488 |
| Model 6 | ln(B) = a + bln(DBH) | −6.256 | 3.100 | 0.959 | 0.035 | −71.480 | <0.0001 | 1.0005 | 2.8 × 10−5 | 0.002 | 0.032 | 0.535 |
| Equations using height as the predictor | ||||||||||||
| Model 7 | ln(B) = a + bln(HT) | 2.616 | 1.604 | 0.824 | 0.074 | −55.383 | 0.0001 | 1.0022 | 12.3 × 10−5 | 0.012 | 0.067 | 1.112 |
| Model 8 | ln(B) = a + bln(HTOT) | −0.443 | 2.333 | 0.562 | 0.117 | −45.350 | 0.008 | 1.0056 | 30.4 × 10−5 | 0.030 | 0.106 | 1.755 |
| Allometric Equations Using DBH and Height as Composite Predictors | ||||||||||||
| Model 9 | ln(B) = a + bln(DBH2HT) | −2.335 | 0.832 | 0.942 | 0.042 | −67.606 | <0.0001 | 1.0007 | 4 × 10−5 | 0.004 | 0.038 | 0.638 |
| Allometric Equations Using DBH, Height and Infra-Density as Composite Predictors | ||||||||||||
| Model 10 | ln(B) = bln(DBH2HT ρ) | 0.683 | 0.999 | 0.0439 | −68.560 | 0.0001 | 1.0008 | −2.1 × 10−5 | −0.002 | 0.040 | 0.669 | |
| Model 11 | ln(B) = a + bln(DBH2HT ρ) | 0.277 | 0.651 | 0.938 | 0.043 | −66.938 | <0.0001 | 1.0008 | 4.3 × 10−5 | 0.004 | 0.039 | 0.658 |
| Allometric Equations Using DBH, HT, ρ or NF as Composite Variables to Estimate Aboveground Biomass from Its Components (Stems, Rachises, Leaves with/without Rachises) | ||||||||||||
| Model 12 | ln(BStem) = a + bln(DBH) | −6.776 | 3.147 | 0.930 | 0.048 | −64,933 | <0.0001 | 1.0010 | 5.6 × 10−5 | 0.005 | 0.043 | 0.762 |
| ln(BLeaf) = a + b(DBH) | −7.188 | 3.014 | 0.679 | 0.115 | −45,605 | 0.002 | 1.0055 | 51.4 × 10−5 | 0.051 | 0.104 | 2.197 | |
| Model 13 | ln(BStem) = a + bln(DBH2HT) | −2.831 | 0.848 | 0.921 | 0.051 | −63,594 | <0.0001 | 1.0010 | 6.4 × 10−5 | 0.006 | 0.046 | 0.810 |
| ln(BFSR) = a + bln(DBH2HTNF) | −3.124 | 0.530 | 0.564 | 0.146 | −40,430 | 0.008 | 1.0088 | 115.1 × 10−5 | 0.115 | 0.132 | 3.257 | |
| ln(BRachis) = a + bln(DBH2HTNF) | −4.041 | 0.597 | 0.702 | 0.122 | −44,332 | 0.001 | 1.0062 | 74.9 × 10−5 | 0.074 | 0.111 | 2.724 | |
| Model 14 | ln(BStem) = bln(DBH2HT ρ) | 0.645 | 0.999 | 0.037 | −71.844 | <0.0001 | 1.0006 | 11 × 10−5 | 0.011 | 0.034 | 0.610 | |
| ln(BLeaf) = bln(DBH2HTNF) | 0.351 | 0.999 | 0.103 | −46.406 | <0.0001 | 1.0061 | 109.6 × 10−5 | 0.109 | 0.110 | 2.320 | ||
| Model 15 | ln(BStem) = a + bln(DBH2HT ρ) | −0.295 | 0.678 | 0.958 | 0.037 | −70.429 | <0.0001 | 1.0006 | 3.4 × 10−5 | 0.003 | 0.033 | 0.594 |
| ln(BLeaf) = a + bln(DBH2HTNF) | −2.852 | 0.561 | 0.747 | 0.103 | −48.205 | 0.001 | 1.0043 | 40.4 × 10−5 | 0.040 | 0.093 | 1.952 | |
| Model | r2 | AIC | p | ER | %ER | RMSE | %RMSE |
|---|---|---|---|---|---|---|---|
| Model 1: ln(ρ) = a + b × ln(DBH) | 0.787 | −60.077 | 0.008 | 0.034 | 3.407 | 0.014 | 4.845 |
| Model 2: ln(NF) = a + b × ln(DBH) | 0.750 | 13.371 | 0.012 | 0.075 | 7.552 | 3.098 | 9.638 |
| Model 3: ln(HT) = a + b × ln(DBH) | 0.660 | −3.111 | 0.026 | 0.0006 | 0.068 | 0.645 | 7.697 |
| Model 4: ln(HTOT) = a + b × ln(DBH) | 0.927 | −15.660 | 0.001 | 0.001 | 0.136 | 0.583 | 3.712 |
| Model | r2 | AIC | P | ER | %ER | RMSE | %RMSE |
|---|---|---|---|---|---|---|---|
| Allometric Equations Using a Single Explanatory Variable, i.e., Infra-Density or DBH | |||||||
| Model 6: ln(B) = a + bln(DBH) | 0.887 | 49.601 | 0.002 | 0.091 | 9.109 | 45.386 | 11.253 |
| Model 5: ln(B) = a +bln(ρ) | 0.757 | 54.962 | 0.011 | 0.010 | 1.079 | 38.143 | 9.457 |
| Allometric Equations Using Height as an Explanatory Variable | |||||||
| Model 8: ln(B) = a +bln(HTOT) | 0.730 | 55.712 | 0.014 | 0.012 | 1.242 | 41.954 | 10.402 |
| Model 7: ln(B) = a + bln(HT) | 0.810 | 53.234 | 0.006 | 0.042 | 4.157 | 38.854 | 9.633 |
| Allometric Equations Using DBH and Height as Compound Explanatory Variables | |||||||
| Model 9: ln(B) = a + bln(DBH2HT) | 0.939 | 45.305 | 0.0003 | 0.065 | 6.501 | 33.027 | 8.188 |
| Allometric Equations Using DBH, Height, and ρ as Compound Explanatory Variables | |||||||
| Model 10: ln(B) = bln(DBH2HT ρ) | 0.961 | 42.153 | 0.0001 | 0.048 | 4.815 | 26.786 | 6.641 |
| Model 11: ln(B) = a + bln(DBH2HT ρ) | 0.961 | 42.206 | 0.0001 | 0.042 | 4.247 | 23.339 | 5.786 |
| Allometric Equations Using Biomass Components (Stems, Rachises, Leaves with/without Rachis) | |||||||
| Model 12: ln(B) = [ln(BStem) + ln(BLeaf)] = [a1+b1ln(DBH) + a2+b2ln(DBH)] | 0.887 | 49.605 | 0.002 | 0.089 | 8,916 | 44.856 | 11.121 |
| Model 13: ln(B) = [ln(BStem) + ln(BFSR) + ln(BRachis)] = [a1+b1ln(DBH2HT) + a2+b2ln(DBH2HTNF) + a3+b3ln(DBH2HTNF)] | 0.956 | 42.950 | 0.0001 | 0.052 | 5.268 | 27.325 | 6.774 |
| Model 14: ln(B) = [ln(BStem) + ln(BLeaf)] = [b1ln(DBH2HTρ) + b2ln(DBH2HTNF)] | 0.969 | 40.519 | < 0.0001 | 0.044 | 4.420 | 21.352 | 5.294 |
| Model 15: [BStem + BLeaf] = [a1 + b1ln(DBH2HTρ) + a2 + b2ln(DBH2HTNF)] | 0.972 | 39.922 | < 0.0001 | 0.036 | 3.684 | 20.692 | 5.130 |
| Reference | Name | ER | %ER | RMSE | %RMSE |
|---|---|---|---|---|---|
| Allometric Equations Using Height as an Explanatory Variable | |||||
| Khalid et al. [4] | Khal1999 | 1.725 | 172.583 | 669.968 | 166.109 |
| Thenkabail et al. [20] (Dry biomass model) | Thenk2004b | −0.198 | −19.838 | 96.752 | 23.988 |
| Thenkabail et al. [20] (Fresh biomass model) | Thenk2004a | −0.077 | −7.752 | 55.317 | 13.715 |
| This study | Model 7 | 0.042 | 4.157 | 38.854 | 9.633 |
| Allometric Equations Using DBH and Height as Compound Explanatory Variables | |||||
| Saldarriaga et al. [18] | Sald1988 | −0.999 | −99.999 | 410.677 | 101.821 |
| Hughes et al. [25] | Flyn1999 | −0.999 | −99.996 | 410.664 | 101.818 |
| This study | Model 9 | 0.065 | 6.501 | 33.027 | 8.188 |
| Allometric Equations Using DBH, Height and Infra-Density or Dry Mass Fraction as Composite Explanatory Variables | |||||
| Goodman et al. [27] | Good2013 | −0.994 | −99.408 | 408.402 | 101.257 |
| Da Silva et al. [22] (Not compartmentalized allometric biomass model) | DaSil2015a | 0.024 | 2.413 | 37.699 | 9.347 |
| This study | Model 11 | 0.042 | 4.247 | 23.339 | 5.786 |
| Allometric Equations Estimating Aboveground Biomass (B) from Biomass Components (Stems, Leaves or Rachis) Using DBH, HT and ρ or NF | |||||
| Cole and Ewel [26] | ColEwe2006 | −0.211 | −21.122 | 92.841 | 23.018 |
| Da Silva et al. [22] (Compartmentalized allometric biomass model) | DaSil2015b | 0.050 | 5.007 | 44.157 | 10.948 |
| This study | Model 15 | 0.036 | 3.684 | 20.692 | 5.130 |
© 2020 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Migolet, P.; Goïta, K.; Ngomanda, A.; Mekui Biyogo, A.P. Estimation of Aboveground Oil Palm Biomass in a Mature Plantation in the Congo Basin. Forests 2020, 11, 544. https://doi.org/10.3390/f11050544
Migolet P, Goïta K, Ngomanda A, Mekui Biyogo AP. Estimation of Aboveground Oil Palm Biomass in a Mature Plantation in the Congo Basin. Forests. 2020; 11(5):544. https://doi.org/10.3390/f11050544
Chicago/Turabian StyleMigolet, Pierre, Kalifa Goïta, Alfred Ngomanda, and Andréana Paola Mekui Biyogo. 2020. "Estimation of Aboveground Oil Palm Biomass in a Mature Plantation in the Congo Basin" Forests 11, no. 5: 544. https://doi.org/10.3390/f11050544
APA StyleMigolet, P., Goïta, K., Ngomanda, A., & Mekui Biyogo, A. P. (2020). Estimation of Aboveground Oil Palm Biomass in a Mature Plantation in the Congo Basin. Forests, 11(5), 544. https://doi.org/10.3390/f11050544