Quality and Price of Spruce Logs, Determined Conventionally and by Dendrochronological and NDE Techniques
Abstract
:1. Introduction
2. Materials and Methods
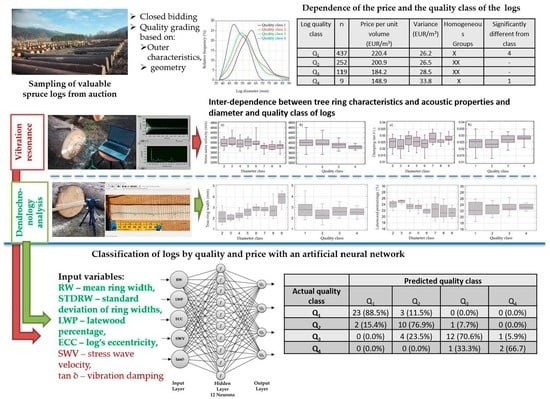
2.1. Log Sampling
2.2. Visual Determination of Log Quality According to Standards
2.3. Determination of Stress Wave Velocity and Vibration Damping in Logs by Vibration Resonance Method

2.4. Dendrochronological Measurements and Analysis
2.5. Data Analysis and Modelling
3. Results and Discussion
3.1. Interdependence between Quality According to Standards, Geometric Characteristics of Logs, and Tree-Ring Characteristics
3.2. Log Characteristics and Quality Evaluated by Stress Wave Velocity
3.3. Relationship between the Technological Characteristics of Logs and the Price
3.4. Artificial Neural Network Analysis
4. Conclusions
Author Contributions
Funding
Data Availability Statement
Acknowledgments
Conflicts of Interest
References
- Wagenführ, R. Holzatlas, 4th ed.; Fachbuchverlag: Leipzig, Germany, 2014; p. 688. [Google Scholar]
- Øvrum, A.; Vestøl, G.I. Modeling the effect of length on yield of sawn timber grades in Norway spruce (Picea abies (L.) Karst.). Eur. J. Wood Wood Prod. 2009, 67, 63–70. [Google Scholar] [CrossRef]
- Ovrum, A.; Hoibo, O.A.; Vestol, G.I. Grade yield of lumber in Norway spruce (Picea abies (L.) Karst.) as affected by forest quality, tree size and log length. For. Prod. J. 2009, 59, 70–78. [Google Scholar]
- Rais, A.; Pretzsch, H.; Kuilen, J.W.G. Roundwood pre-grading with longitudinal acoustic waves for production of structural boards. Eur. J. Wood Wood Prod. 2014, 72, 87–98. [Google Scholar] [CrossRef]
- Blouin, D.; Beaulieu, J.; Daoust, G.; Poliquin, J. Wood quality of Norway spruce grown in plantations in Quebec. Wood Fiber Sci. 1994, 26, 342–353. [Google Scholar]
- Edlund, J. Automatic grading of softwood sawlogs for pricing using external geometry. Scand. J. For. Res. 2004, 19, 38–47. [Google Scholar] [CrossRef]
- Pretzsch, H.; Rais, A. Wood quality in complex forests versus even-aged monocultures: Review and perspectives. Wood Sci. Technol. 2016, 50, 845–880. [Google Scholar] [CrossRef]
- Carlier, C.; Bremaud, I.; Gril, J. Violin making ‘tonewood’: Comparing makers’ empirical expertise with wood structural/visual and acoustical properties. In Proceedings of the International Symposium on Musical Acoustics ISMA2014, La Mans, France, 7–12 July 2014; pp. 325–330. [Google Scholar]
- Buksnowitz, C.; Teischinger, A.; Müller, U.; Pahler, A.; Evans, R. Resonance wood [Picea abies (L.) Karst.]—Evaluation and prediction of violin makers’ quality grading. J. Acoust. Soc. Am. 2007, 121, 2384–2395. [Google Scholar] [CrossRef]
- Service, S.F. Poročilo Zavoda za Gozdove Slovenije o Gozdovih; Slovenian Forestry Service: Ljubljana, Slovenia, 2020; p. 125. [Google Scholar]
- Diaci, J. Regeneration dynamics in a Norway spruce plantation on a silver fir-beech forest site in the Slovenian Alps. For. Ecol. Manag. 2002, 161, 27–38. [Google Scholar] [CrossRef]
- CEN. Qualitative classification of softwood round timber—Part 1: Spruces and firs. In EN 1927-1; CEN: Brussels, Belgium, 2008; Volume EN 1927-1, p. 11. [Google Scholar]
- Mäkelä, A.; Grace, J.C.; Deckmyn, G.; Kantola, A.; Campioli, M. Simulating wood quality in forest management models. For. Syst. 2010, 19, 48–68. [Google Scholar] [CrossRef]
- Repola, J. Models for Vertical Wood Density of Scots Pine, Norway Spruce and Birch Stems, and Their Application to Determine Average Wood Density. Silva Fenica 2006, 40, 673–685. [Google Scholar] [CrossRef] [Green Version]
- Meyers, M.A. Dynamic Behaviour of Materials; Willey & Sons: New York, NY, USA, 1994; p. 688. [Google Scholar]
- Bucur, V. Acoustics of Wood; Springer: Berlin/Heidelberg, Germany, 2006; p. 393. [Google Scholar]
- Rafiq, M.Y.; Bugmann, G.; Easterbrook, D.J. Neural network design for engineering applications. Comput. Struct. 2001, 79, 1541–1552. [Google Scholar] [CrossRef]
- Esteban, L.G.; Fernandez, F.G.; de Palacios, P. MOE prediction in Abies pinsapo Boiss. timber: Application of an artificial neural network using non-destructive testing. Comput. Struct. 2009, 87, 1360–1365. [Google Scholar] [CrossRef]
- Schmoldt, D.L.; He, J.; Abbot, A.L. Automated labelling of logs features in CT imagery of multiple hardwood species. Wood Fiber Sci. 2000, 32, 287–300. [Google Scholar]
- Nasir, V.; Nourian, S.; Avramidis, S.; Cool, J. Classification of thermally treated wood using machine learning technques. Wood Sci. Technol. 2019, 53, 275–288. [Google Scholar] [CrossRef]
- Nordmark, U. Knot Identification from CT images of Young Pinus sylvestris Sawlogs Using Artificial Neural Networks. Scand. J. For. Res. 2002, 17, 72–78. [Google Scholar] [CrossRef]
- Šilinskas, B.; Varnagiryte-Kabašinskiene, I.; Aleinikovas, M.; Beniušiene, L.; Aleinikoviene, J.; Škema, M. Scots Pine and Norway Spruce Wood Properties at Sites with Different Stand Densities. Forests 2020, 11, 587. [Google Scholar] [CrossRef]
- Wimmer, R.; Downes, G.M. Temporal variation of the ring width - wood density relationship in Norway spruce grown under two levels of anthropogenic disturbance. IAWA J. 2003, 24, 53–61. [Google Scholar] [CrossRef]
- Dutilleul, P.; Herman, M.; Avella Shaw, T. Growth rate effects on correlations among ring width, wood density, and mean tracheid length in Norway spruce (Picea abies). Can. J. For. Res. 1998, 28, 56–68. [Google Scholar] [CrossRef]
- Olesen, P.O. The interrelation between basic density and ring width of Norway spruce. Forstl. I. Dan. 1976, 34, 339–359. [Google Scholar]
- Koch, G.; Schwab, E.; Kruse, K.; Bauch, J. Untersuchung der dynamischen Belastbarkeit des Holzes sekundär geschädigter Fichten (Picea abies [L.] Karst.) aus extrem windexponierten Hochlagen des Ostererzgebirges. Holz Roh.-Und Werkst. 1996, 54, 313–319. [Google Scholar] [CrossRef]
- Wimmer, R.; Grabner, M. Effects of climate on vertical resin duct density and radial growth of Norway spruce (Picea abies (L.) Karst.). Trees 1997, 11, 271–276. [Google Scholar] [CrossRef]
- Gričar, J.; Čufar, K.; Eler, K.; Gryc, V.; Vavrčik, H.; de Luis, M.; Prislan, P. Transition Dates from Earlywood to Latewood and Early Phloem to Late Phloem in Norway Spruce. Forests 2021, 12, 331. [Google Scholar] [CrossRef]
- Sonderegger, W.; Mandallaz, D.; Niemz, P. An investigation of the influence of selected factors on the properties of spruce wood. Wood Sci. Technol. 2007, 42, 281–298. [Google Scholar] [CrossRef] [Green Version]
- Bergqvist, G. Wood density traits in Norway spruce understorey: Effects of growth rate and birch shelterwood density. Ann. Des Sci. For. 1998, 55, 809–821. [Google Scholar] [CrossRef]
- Franceschini, T.; Longuetaud, F.; Bontemps, J.D.; Bouriaud, O.; Caritey, B.D.; Leban, J.M. Effect of ring width, cambial age, and climatic variables on the within-ring wood density profile of Norway spruce Picea abies (L.) Karst. Trees 2013, 27, 913–925. [Google Scholar] [CrossRef]
- Glos, P.; Pahler, A. Fichtenstarkholz—Problemsortiment oder Chance? Schweiz. Z. Für. Forstwes. 2006, 157, 539–545. [Google Scholar] [CrossRef] [Green Version]
- Teschinger, A.; Müller, U. Holzeigenschaften von Nadelstarkholz und sein technologisches Potenzial. Schweiz. Z. Für. Forstwes. 2006, 157, 561–564. [Google Scholar] [CrossRef]
- Chauhan, S.S.; Walker, J.C.F. Variation in acoustic velocity and density with age, and their interrelationships in radiata pine. For. Ecol. Manag. 2006, 229, 388–394. [Google Scholar] [CrossRef]
- Legg, M.; Bradley, S. Measurement of stiffness of standing trees and felled logs using acoustics: A review. J. Acoust. Soc. Am. 2016, 139, 588–604. [Google Scholar] [CrossRef] [Green Version]
- Tsehaye, A.; Buchanan, A.H.; Walker, J.C.F. Sorting of logs using acoustics. Wood Sci. Technol. 2000, 34, 337–344. [Google Scholar] [CrossRef]
- Wang, X.; Ross, R.J.; Punches, J.; Erickson, J.R.; Pellerin, R.F. Diameter effect on stress-wave evaluation of modulus of elasticity of logs. Wood Fiber Sci. 2004, 36, 368–377. [Google Scholar]
- Machek, L.; Militz, R.H.; Sierra, A. As the influence of wood moisture content on dynamic modulus of elasticity measurements in durability testing. Holzforsch. Holzverwert. 2001, 53, 97–100. [Google Scholar]
- Barrett, J.D.; Hong, J.P. Moisture content adjustments for dynamic modulus of elasticity of wood members. Wood Sci. Technol. 2009, 44, 485–495. [Google Scholar] [CrossRef]
- Ouis, D. On the frequency dependence of the modulus of elasticity of wood. Wood Sci. Technol. 2002, 36, 335–346. [Google Scholar] [CrossRef]
- Woodhouse, J. Linear damping models for structural vibration. J. Sound Vib. 1998, 215, 547–569. [Google Scholar] [CrossRef]
- Ouis, D. Vibrational and acoustical experiments on logs of spruce. Wood Sci. Technol. 1999, 33, 151–184. [Google Scholar] [CrossRef]
- Ouis, D. Detection of decay in logs through measuring the dampening of bending vibrations by means of a room acoustical technique. Wood Sci. Technol. 2000, 34, 221–236. [Google Scholar] [CrossRef]
- Barré, J.B.; Bourrier, F.; Brancheriau, L.; Rey, F.; Bertrand, D. Effects of fungal decay on elasticity and damping of small-diameter silver fir logs assessed by the transverse vibration resonant method. Wood Sci. Technol. 2018, 52, 403–420. [Google Scholar] [CrossRef] [Green Version]
- Kantola, A.; Song, T.; Usenius, A.; Heikkilä, A. Simulated yield and quality distribution of sawn timber from final felling in a Norway spruce [Picea abies (L.) Karst.] stand with varying thinning regimes: A case study. Wood Mater. Sci. Eng. 2009, 4, 87–97. [Google Scholar] [CrossRef]
- Fischer, C.; Vestøl, G.L.; Øvrum, A.; Høibø, O.A. Pre-sorting of Norway spruce structural timber using acoustic measurements combined with site-, tree- and log characteristics. Eur. J. Wood Wood Prod. 2015, 73, 819–828. [Google Scholar] [CrossRef]
- Edlund, J.; Lindström, H.; Nilsson, F.; Reale, M. Modulus of elasticity of Norway spruce saw logs vs. structural lumber grade. Holz Roh.-Und Werkst. 2006, 64, 273–279. [Google Scholar] [CrossRef]
- Mäkinen, H.; Verkasalo, E.; Tuimala, A. Effects of pruning in Norway spruce on tree growth and grading of sawn boards in Finland. Forestry 2014, 87, 417–424. [Google Scholar] [CrossRef] [Green Version]
- Kamal, K.; Qayyum, R.; Mathavan, S.; Zafar, T. Wood defects classification using laws texture energy measures and supervised learning approach. Adv. Eng. Inform. 2017, 34, 125–135. [Google Scholar] [CrossRef]
- Gobakken, T. The Effect of Two Different Price Systems on the Value and Cross-cutting Patterns of Norway Spruce Logs. Scand. J. For. Res. 2000, 15, 368–377. [Google Scholar] [CrossRef]
- Hlavackova, P.; Brezina, D.; Sujova, A. The Price Formation of Raw Wood in the Czech Republic and a Comparison with the Neighbor States. Procedia Econ. Financ. 2015, 26, 389–395. [Google Scholar] [CrossRef] [Green Version]
- Malinen, J.; Kilpeläinen, H. Price Systems for Standing Sales of Industrial Roundwood in Finland. Balt. For. 2013, 19, 307–315. [Google Scholar]











| Characteristics | Quality Class | ||||||
|---|---|---|---|---|---|---|---|
| Q1 | Q2 | Q3 | Q4 | Q5 | |||
| Dimensions of log | Mean diameter (cm) | >45 | >40 | > 35 < 55 | >20 | >20 | |
| Length (m) | >3 | >3 | >3 | >3 | >3 | ||
| Knots | Sound | N.A. | N.A. | N.A. | D ≤ 4 cm | D ≤ 8 cm | |
| Dead | N.A. | N.A. | N.A. | N.A. | D ≤ 4 cm | ||
| Eccentricity [%] | N.A. | N.A. | ≤10 | ≤15 | unlimited | ||
| Sweep [cm/m] | 20 ≤ D ≤ 35 cm | N.A. | N.A. | - | ≤1.0 | ≤2.0 | |
| D ≥ 35 cm | ≤1.0 | ≤1.5 | ≤2.0 | ||||
| Taper | Length ≤ 6 m | 20 ≤ D ≤ 35 cm | N.A. | N.A. | - | ≤1.2 | ≤1.7 |
| D ≥ 35 cm | - | ≤1.7 | ≤2.6 | ||||
| Length > 6 m | 20 ≤ D ≤ 35 cm | - | - | - | ≤1.1 | ≤1.4 | |
| D ≥ 35 cm | - | ≤1.3 | ≤1.6 | ||||
| Heart cracks | N.A. | N.A. | ≤D/4 | ≤D/3 | ≤D/2 | ||
| Ring shakes | N.A. | N.A. | N.A. | ≤D/4 | ≤D/3 | ||
| Number of Tree Rings | ||||||
|---|---|---|---|---|---|---|
| Quality Class | Number of Logs | Mean | St.dev | CoV (%) | Minimum | Maximum |
| Q1 | 26 | 121 | 19.5 | 15.7% | 96 | 167 |
| Q2 | 13 | 118 | 17.0 | 10.1% | 90 | 153 |
| Q3 | 17 | 111 | 12.6 | 17.6% | 79 | 145 |
| Q4 | 3 | 104 | 12.0 | 11.6% | 74 | 138 |
| Total | 59 | 113 | 15.3 | 13.7% | 74 | 167 |
| Source | Sum of Squares | Df | Mean Square | F-Ratio | p-Value |
|---|---|---|---|---|---|
| MAIN EFFECTS | |||||
| A: Diameter class | 1.415 · 106 | 8 | 176,905.0 | 8.96 | 0.000 |
| B: Quality class | 159,832.0 | 4 | 53,277.4 | 2.70 | 0.045 |
| C: Length class | 99,810.7 | 3 | 33,270.2 | 1.68 | 0.169 |
| RESIDUAL | 1.584 · 107 | 802 | 19,753.0 | ||
| TOTAL (CORRECTED) | 1.787 · 107 | 816 |
| Diameter Class | Diameter (cm) | n | Price per Unit Volume (EUR/m3) | Variance (EUR/m3) | Homogeneous Groups | Significantly Different from Class |
|---|---|---|---|---|---|---|
| 2 | 45–49 | 73 | 113.3 | 32.1 | X | 5, 6, 7, 8, 9 |
| 3 | 50–54 | 157 | 135.7 | 30.1 | XX | 6, 7, 8, 9 |
| 4 | 55–59 | 181 | 159.6 | 29.7 | XX | 6, 7, 8, 9 |
| 5 | 60–64 | 189 | 180.7 | 29.4 | XX | 8, 9 |
| 6 | 65–69 | 93 | 218.1 | 31.7 | X | 1, 2, 8, 9 |
| 7 | 70–74 | 65 | 219.4 | 33.5 | X | 1, 2, 8, 9 |
| 8 | 75–79 | 32 | 277.7 | 38.5 | X | 1, 2, 3, 4, 5, 6, 7 |
| 9 | >80 | 27 | 280.3 | 37.5 | X | 1, 2, 3, 4, 5, 6, 7 |
| Log Quality Class | n | Price per Unit Volume (EUR/m3) | Variance (EUR/m3) | Homogeneous Groups | Significantly Different from Class |
|---|---|---|---|---|---|
| Q1 | 437 | 220.4 | 26.2 | X | 4 |
| Q2 | 252 | 200.9 | 26.5 | XX | - |
| Q3 | 119 | 184.2 | 28.5 | XX | - |
| Q4 | 9 | 148.9 | 33.8 | X | 1 |
| Predicted Quality Class | ||||
|---|---|---|---|---|
| Actual Quality Class | Q1 | Q2 | Q3 | Q4 |
| Q1 | 23 (88.5%) | 3 (11.5%) | 0 (0.0%) | 0 (0.0%) |
| Q2 | 2 (15.4%) | 10 (76.9%) | 1 (7.7%) | 0 (0.0%) |
| Q3 | 0 (0.0%) | 4 (23.5%) | 12 (70.6%) | 1 (5.9%) |
| Q4 | 0 (0.0%) | 0 (0.0%) | 1 (33.3%) | 2 (66.7%) |
| Predicted Price Class | |||||||||
|---|---|---|---|---|---|---|---|---|---|
| Actual Price Class | P1 | P2 | P3 | P4 | P5 | P6 | P7 | P8 | P9 |
| P1 | 8 (100%) | 1 (12.5%) | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) |
| P2 | 1 (4.0%) | 22 (88%) | 2 (8.0%) | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) |
| P3 | 0 (0.0%) | 1 (11.1%) | 7 (77.8%) | 1 (11.1%) | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) |
| P4 | 0 (0.0%) | 0 (0.0%) | 2 (40.0%) | 3 (60.0%) | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) |
| P5 | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) | 2 (50.0%) | 2 (50.0%) | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) |
| P6 | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) | 2 (66.7%) | 1 (33.3%) | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) |
| P7 | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) | 1 (50.0%) | 0 (0.0%) | 1 (50.0%) | 0 (0.0%) | 0 (0.0%) |
| P8 | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) | 1 (50.0%) | 1 (50.0%) | 0 (0.0%) | 0 (0.0%) |
| P9 | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) | 0 (0.0%) | 1 (100.0%) | 0 (0.0%) | 0 (0.0%) |
Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Straže, A.; Novak, K.; Čufar, K. Quality and Price of Spruce Logs, Determined Conventionally and by Dendrochronological and NDE Techniques. Forests 2022, 13, 729. https://doi.org/10.3390/f13050729
Straže A, Novak K, Čufar K. Quality and Price of Spruce Logs, Determined Conventionally and by Dendrochronological and NDE Techniques. Forests. 2022; 13(5):729. https://doi.org/10.3390/f13050729
Chicago/Turabian StyleStraže, Aleš, Klemen Novak, and Katarina Čufar. 2022. "Quality and Price of Spruce Logs, Determined Conventionally and by Dendrochronological and NDE Techniques" Forests 13, no. 5: 729. https://doi.org/10.3390/f13050729
APA StyleStraže, A., Novak, K., & Čufar, K. (2022). Quality and Price of Spruce Logs, Determined Conventionally and by Dendrochronological and NDE Techniques. Forests, 13(5), 729. https://doi.org/10.3390/f13050729