The Trends and Future Prospective of In Silico Models from the Viewpoint of ADME Evaluation in Drug Discovery
Abstract
:1. Introduction
2. Evaluation Metrics of Predictive Models
- Classification model evaluation metrics
- b.
- Regression model evaluation metrics:
3. Physicochemical Properties
3.1. Lipophilicity
3.2. Solubility
3.3. Ionization
3.4. Topology
3.5. Molecular Weight
4. Oral Absorption
4.1. General Assessment
4.2. Solubility Prediction
4.3. Prediction of Membrane Permeability
4.4. Prediction of Intestinal Absorption
5. Distribution
5.1. General Assessment
5.2. Prediction of Tissue Distribution
5.3. Prediction of Human Plasma (Serum) Protein Binding
5.4. Prediction of Brain Distribution
5.4.1. General Assessment of Drug Concentrations in the Brain
5.4.2. Prediction of Brain-to-Plasma Concentration Ratio (BBB Permeability)
5.4.3. Unbound Brain-To-Plasma Partition Coefficient and Brain Homogenate Binding
| Parameter | Data Set | Type of Model | Algorithm, Descriptors or Equation of Model | Predictive Performance | Ref. | |
|---|---|---|---|---|---|---|
| No of cpds | Source | |||||
| fu,brain | 470 | Experimental data | QSAR | Nonlinear least-squares minimization with log P and pKa | R2 = 0.75 | [74] |
| fu,brain | 2292 | In-house data | QSAR | SVM | R2 = 0.64 | [90] |
| fu,brain | 24 | Commercial CNS drugs | QSAR | SVM | R2 = 0.782 | [92] |
| Kp,uu,brain | 246 for direct model, 173 for indirect model | In-house cpds, research | QSAR | RF, SVM | Indirect model: R2 = 0.79–0.9, direct model R2 = 0.94–0.96 | [86] |
| Kp,uu,brain | 346 | In-house cpds, research | QSAR | RF, SVM | Q2 = 0.73–0.80 | [87] |
| Kp,uu,brain | 43 | Selected from 92 drugs | QSAR | PLS model, 16 descriptors | Q2 = 0.452 | [91] |
| Kp,uu,brain | 640 | In-house cpds | QSAR | RF, Conjugate gradient optimization (GPOPT) or incorporation of in vitro data | R2 = 0.489 for RF, 0.536 for GPOPT | [93] |
| Kp,uu,brain | 241 | Developmental cpds and marketed drugs | linear regression | A quantum-mechanics-based energy of solvation (E-sol), a linear regression model based on E-sol vs. Kp,uu,brain linear | Accuracy = 0.79, R2 = 0.61 | [94] |
5.4.4. P-gp-Related Prediction Models
6. Metabolism
6.1. General Assessment
6.2. Prediction of Microsomal Metabolic Stability
6.3. Prediction of Total Clearance
6.4. Molecular Modeling and Simulation
7. Renal Excretion
7.1. General Assessment
7.2. Prediction of Renal Clearance
7.3. Prediction of the Fraction of Urinary Excretion
8. Prediction of Transporter Substrates Involved in ADME
9. Toxicity
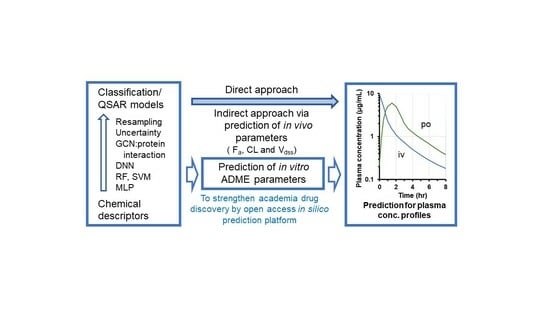
10. In Silico Prediction Models Applicable to Academic Research
11. Future Prospective and Conclusions
Author Contributions
Funding
Institutional Review Board Statement
Informed Consent Statement
Data Availability Statement
Conflicts of Interest
References
- Daoud, N.E.; Borah, P.; Deb, P.K.; Venugopala, K.N.; Hourani, W.; Alzweiri, M.; Bardaweel, S.K.; Tiwari, V. ADMET profiling in drug discovery and development: Perspectives of in silico, in vitro and integrated approaches. Curr. Drug Metab. 2021, 22, 503–522. [Google Scholar] [CrossRef]
- de Souza Neto, L.R.; Moreira-Filho, J.T.; Neves, B.J.; Maidana, R.L.B.R.; Guimarães, A.C.R.; Furnham, N.; Andrade, C.H.; Silva, F.P., Jr. In silico strategies to support fragment-to-lead optimization in drug discovery. Front. Chem. 2020, 18, 93. [Google Scholar] [CrossRef] [PubMed]
- Ferreira, L.L.G.; Andricopulo, A.D. ADMET modeling approaches in drug discovery. Drug Discov. Today 2019, 24, 1157–1165. [Google Scholar] [CrossRef]
- Ding, Y.; Jiang, X.; Kim, Y. Relational graph convolutional networks for predicting blood-brain barrier penetration of drug molecules. Bioinformatics 2022, 38, 2826–2831. [Google Scholar] [CrossRef] [PubMed]
- Jiang, D.; Wu, Z.; Hsieh, C.Y.; Chen, G.; Liao, B.; Wang, Z.; Shen, C.; Cao, D.; Wu, J.; Hou, T. Could graph neural networks learn better molecular representation for drug discovery? A comparison study of descriptor-based and graph-based models. J. Cheminform. 2021, 13, 12. [Google Scholar] [CrossRef] [PubMed]
- Kinch, M.S.; Horn, C.; Kraft, Z.; Tyler Schwartz, T. Expanding roles for academic entrepreneurship in drug discovery. Drug Discov. Today 2020, 25, 1905–1909. [Google Scholar] [CrossRef] [PubMed]
- Bryans, J.S.; Kettleborough, C.A.; Solari, R. Are academic drug discovery efforts receiving more recognition with declining industry efficiency? Expert. Opin. Drug Discov. 2019, 14, 605–607. [Google Scholar] [CrossRef] [PubMed]
- Sushko, I.; Novotarskyi, S.; Körner, R.; Pandey, A.K.; Rupp, M.; Teetz, W.; Brandmaier, S.; Abdelaziz, A.; Prokopenko, V.V.; Tanchuk, V.Y.; et al. Online chemical modeling environment (OCHEM): Web platform for data storage, model development and publishing of chemical information. J. Comput. Aided Mol. Des. 2011, 25, 533–554. [Google Scholar] [CrossRef] [PubMed]
- Daina, A.; Michielin, O.; Zoete, V. SwissADME: A free web tool to evaluate pharmacokinetics, drug-likeness and medicinal chemistry friendliness of small molecules. Sci. Rep. 2017, 7, 42717. [Google Scholar] [CrossRef] [PubMed]
- Pires, D.E.V.; Blundell, T.L.; Ascher, D.B. pkCSM: Predicting Small-molecule pharmacokinetic and toxicity properties using graph-based signatures. J. Med. Chem. 2015, 58, 4066–4072. [Google Scholar] [CrossRef] [PubMed]
- Komura, H.; Watanabe, R.; Kawashima, H.; Ohashi, R.; Kuroda, M.; Sato, T.; Honma, T.; Mizuguchi, K. A public-private partnership to enrich the development of in silico predictive models for pharmacokinetic and cardiotoxic properties. Drug Discov. Today 2021, 26, 1275–1283. [Google Scholar] [CrossRef]
- Fedi, A.; Vitale, C.; Ponschin, G.; Ayehunie, S.; Fato, M.; Scaglione, S. In vitro models replicating the human intestinal epithelium for absorption and metabolism studies: A systematic review. J. Control Release 2021, 335, 247–268. [Google Scholar] [CrossRef] [PubMed]
- Di, L.; Artursson, P.; Avdeef, A.; Benet, L.Z.; Houston, J.B.; Kansy, M.; Kerns, E.H.; Lennernäs, H.; Smith, D.A.; Sugano, K. The critical role of passive permeability in designing successful drugs. Chem. Med. Chem. 2020, 15, 1862–1874. [Google Scholar] [CrossRef] [PubMed]
- Shah, V.P.; Amidon, G.L.; Lennernas, H.; Shah, V.P.; Crison, J.R. A theoretical basis for a biopharmaceutic drug classification: The correlation of in vitro drug product dissolution and in vivo bioavailability. Pharm. Res. 1995, 12, 413–420. [Google Scholar] [CrossRef] [PubMed]
- Abuhassan, Q.; Khadra, I.; Pyper, K.; Augustijns, P.; Brouwers, J.; Gavin, W.; Halbert, G.W. Fasted intestinal solubility limits and distributions applied to the biopharmaceutics and developability classification systems. Eur. J. Pharm. Biopharm. 2022, 170, 160–169. [Google Scholar] [CrossRef] [PubMed]
- Walker, M.A. Improvement in aqueous solubility achieved via small molecular changes. Bioorg Med. Chem. Lett. 2017, 27, 5100–5108. [Google Scholar] [CrossRef]
- Wang, S.; Donga, G.; Shenga, C. Structural simplification: An efficient strategy in lead optimization. Acta Pharm. Sin. B 2019, 9, 880–901. [Google Scholar] [CrossRef]
- Sun, H.; Shah, P.; Nguyen, K.; Yu, K.R.; Kerns, E.; Kabir, M.; Wang, Y.; Xu, X. Predictive models of aqueous solubility of organic compounds built on A large dataset of high integrity. Bioorg Med. Chem. 2019, 27, 3110–3114. [Google Scholar] [CrossRef]
- Könczöl, Á.; Gergő Dargó, G. Brief overview of solubility methods: Recent trends in equilibrium solubility measurement and predictive models. Drug Discov. Today Technol. 2018, 27, 3–10. [Google Scholar] [CrossRef] [PubMed]
- Sou, T.; Bergström, C.A.S. Automated assays for thermodynamic (equilibrium) solubility determination. Drug Discov. Today Technol. 2018, 27, 11–19. [Google Scholar] [CrossRef]
- Volpe, D.A. Advances in cell-based permeability assays to screen drugs for intestinal absorption. Expert. Opin. Drug Discov. 2020, 15, 539–549. [Google Scholar] [CrossRef] [PubMed]
- Cai, X.; Patel, S.; Huang, C.; Paiva, A.; Sun, Y.; Barker, G.; Weller, H.; Shou, W. Comprehensive characterization and optimization of Caco-2 cells enabled the development of a miniaturized 96-well permeability assay. Xenobiotica 2022, 52, 742–750. [Google Scholar] [CrossRef] [PubMed]
- Jacobsen, A.; Nielsen, S.; Brandl, M.; Bauer-Brandl, A. Drug permeability profiling using the novel Permeapad® 96-Well plate. Pharm. Res. 2020, 37, 93. [Google Scholar] [CrossRef] [PubMed]
- Williams, J.; Siramshetty, V.; Nguyễn, Ð.; Padilha, E.C.; Kabir, M.; Yu, K.; Wang, A.Q.; Zhao, T.; Itkin, M.; Shinn, P.; et al. Using in vitro ADME data for lead compound selection: An emphasis on PAMPA pH 5 permeability and oral bioavailability. Bioorg Med. Chem. 2022, 56, 116588. [Google Scholar] [CrossRef]
- Ye, D.; Harder, A.; Fang, Z.; Weinheimer, M.; Laplanche, L.; Mezler, M. Characterization and validation of canine P-glycoprotein-deficient MDCK II cell lines for efflux substrate screening. Pharm. Res. 2020, 37, 194. [Google Scholar] [CrossRef]
- Bokulić, A.; Padovan, J.; Stupin-Polančec, D.; Milić, A. Isolation of MDCK cells with low expression of mdr1 gene and their use in membrane permeability screening. Acta Pharm. 2021, 72, 275–288. [Google Scholar] [CrossRef]
- Newby, D.; Freitas, A.A.; Ghafourian, T. Decision trees to characterise the roles of permeability and solubility on the prediction of oral absorption. Eur. J. Med. Chem. 2015, 90, 751–765. [Google Scholar] [CrossRef]
- Siramshetty, V.; Williams, J.; Nguyễn, D.; Neyra, J.; Southall, N.; Mathé, E.; Xu, X.; Shah, P. Validating ADME QSAR models using marketed drugs. SLAS Discov. 2021, 26, 1326–1336. [Google Scholar] [CrossRef]
- Falcón-Cano, G.; Molina, C.; Cabrera-Pérez, M.Á. ADME prediction with KNIME: In silico aqueous solubility consensus model based on supervised recursive random forest approaches. ADMET DMPK 2020, 8, 251–273. [Google Scholar]
- Kamiya, Y.; Omura, A.; Hayasaka, R.; Saito, R.; Sano, I.; Handa, K.; Ohori, J.; Kitajima, M.; Shono, F.; Funatsu, K.; et al. Prediction of permeability across intestinal cell monolayers for 219 disparate chemicals using in vitro experimental coefficients in a pH gradient system and in silico analyses by trivariate linear regressions and machine learning. Biochem. Pharmacol. 2021, 192, 114749. [Google Scholar] [CrossRef]
- Ta, G.H.; Jhang, C.S.; Weng, C.F.; Leong, M.K. Development of a hierarchical support vector regression-based in silico model for Caco-2 permeability. Pharmaceutics 2021, 13, 174. [Google Scholar] [CrossRef] [PubMed]
- Broccatelli, F.; Salphati, L.; Plise, E.; Cheong, J.; Gobbi, A.; Lee, M.L.; Aliagas, I. Predicting passive permeability of drug-like molecules from chemical structure: Where are we? Mol. Pharm. 2016, 13, 4199–4208. [Google Scholar] [CrossRef] [PubMed]
- Lee, M.; Ta, G.H.; Weng, C.; Leong, M.K. In silico prediction of intestinal permeability by hierarchical support vector regression. Int. J. Mol. Sci. 2020, 21, 3582. [Google Scholar] [CrossRef] [PubMed]
- Nakao, K.; Fujikawa, M.; Shimizu, R.; Akamatsu, M. QSAR application for the prediction of compound permeability with in silico descriptors in practical use. J. Comput. Aided Mol. Des. 2009, 23, 309–319. [Google Scholar] [CrossRef] [PubMed]
- Chi, C.; Lee, M.; Weng, C.; Leong, M.K. In silico prediction of PAMPA effective permeability using a two-QSAR approach. Int. J. Mol. Sci. 2019, 20, 3170. [Google Scholar] [CrossRef] [PubMed]
- Bergström, C.A.S.; Larsson, P. Computational prediction of drug solubility in water-based systems: Qualitative and quantitative approaches used in the current drug discovery and development setting. Int. J. Pharm. 2018, 540, 185–193. [Google Scholar] [CrossRef]
- Stenberg, P.; Bergström, C.A.S.; Luthman, K.; Artursson, P. Theoretical predictions of drug absorption in drug discovery and development. Clin. Pharmacokinet. 2002, 41, 877–899. [Google Scholar] [CrossRef] [PubMed]
- van De Waterbeemd, H.; Smith, D.A.; Beaumont, K.; Walker, D.K. Property-based design: Optimization of drug absorption and pharmacokinetics. J. Med. Chem. 2001, 44, 1313–1333. [Google Scholar] [CrossRef]
- Refsgaard, H.H.; Jensen, B.F.; Brockhoff, P.B.; Padkjaer, S.B.; Guldbrandt, M.; Christensen, M.S. In silico prediction of membrane permeability from calculated molecular parameters. J. Med. Chem. 2005, 48, 805–811. [Google Scholar] [CrossRef]
- O’Donovan, D.H.; De Fusco, C.D.; Kuhnke, L.; Reichel, A. Trends in molecular properties, bioavailability, and permeability across the Bayer compound collection. J. Med. Chem. 2023, 66, 2347–2360. [Google Scholar] [CrossRef]
- Shen, J.; Cheng, F.; Xu, Y.; Li, W.; Tang, Y. Estimation of ADME properties with substructure pattern recognition. J. Chem. Inf. Model. 2010, 50, 1034–1041. [Google Scholar] [CrossRef] [PubMed]
- Niwa, T. Using general regression and probabilistic neural networks to predict human intestinal absorption with topological descriptors derived from two-dimensional chemical structures. J. Chem. Inf. Comput. Sci. 2003, 43, 113–119. [Google Scholar] [CrossRef]
- Hou, T.; Wang, J.; Li, Y. ADME evaluation in drug discovery. 8. The prediction of human intestinal absorption by a support vector machine. J. Chem. Inf. Model. 2007, 47, 2408–2415. [Google Scholar] [CrossRef] [PubMed]
- Czub, N.; Szlęk, J.; Pacławski, A.; Klimończyk, K.; Puccetti, M.; Mendyk, A. Artificial intelligence-based quantitative structure-property relationship model for predicting human intestinal absorption of compounds with serotonergic activity. Mol. Pharm. 2023, 20, 2545–2555. [Google Scholar] [CrossRef] [PubMed]
- Obrezanova, O.; Segall, M.D. Gaussian processes for classification: QSAR modeling of ADMET and target activity. J. Chem. Inf. Model. 2010, 50, 1053–1061. [Google Scholar] [CrossRef] [PubMed]
- Basant, N.; Gupta, S.; Singh, K.P. Predicting human intestinal absorption of diverse chemicals using ensemble learning based QSAR modeling approaches. Comput. Biol. Chem. 2016, 61, 178–196. [Google Scholar] [CrossRef]
- Adachi, K.; Utsumi, M.; Sato, T.; Nakano, H.; Shimizu, M.; Yamazaki, H. Modeled Rat hepatic and plasma concentrations of chemicals after virtual administrations using two sets of in silico liver-to-plasma partition coefficients. Biol. Pharm. Bull. 2023, 46, 1316–1323. [Google Scholar] [CrossRef] [PubMed]
- Harrell, A.W.; Sychterz, C.; Ho, M.Y.; Weber, A.; Valko, K.; Negash, K. Interrogating the relationship between rat in vivo tissue distribution and drug property data for >200 structurally unrelated molecules. Pharmacol. Res. Perspect. 2015, 3, e00173. [Google Scholar] [CrossRef] [PubMed]
- Berry, L.M.; Roberts, J.; Be, X.; Zhao, Z.; Lin, M.H. Prediction of V(ss) from in vitro tissue-binding studies. Drug Metab. Dispos. 2010, 38, 115–121. [Google Scholar] [CrossRef] [PubMed]
- Mahmood, I. Prediction of tissue to plasma concentration ratios of drugs in the rat from experimentally estimated volume of distribution: Application of allometry. Curr. Drug Metab. 2018, 19, 155–164. [Google Scholar] [CrossRef]
- Berellini, G.; Springer, C.; Nigel, J.; Waters, J.; Lombardo, F. In silico prediction of volume of distribution in human using linear and nonlinear models on a 669 compound data set. J. Med. Chem. 2009, 52, 4488–4495. [Google Scholar] [CrossRef] [PubMed]
- Paixão, P.; Aniceto, N.; Gouveia, L.F.; Morais, J.A. Prediction of drug distribution in rat and humans using an artificial neural networks ensemble and a PBPK model. Pharm. Res. 2014, 31, 3313–3322. [Google Scholar] [CrossRef] [PubMed]
- Louis, B.; Agrawal, V.K. Prediction of human volume of distribution values for drugs using linear and nonlinear quantitative structure pharmacokinetic relationship models. Interdiscip. Sci. 2014, 6, 71–83. [Google Scholar] [CrossRef] [PubMed]
- Fagerholm, U.; Hellberg, S.; Alvarsson, J.; Arvidsson McShane, S.; Spjuth, O. In silico prediction of volume of distribution of drugs in man using conformal prediction performs on par with animal data-based models. Xenobiotica 2021, 51, 1366–1371. [Google Scholar] [CrossRef] [PubMed]
- Ahmed, H.; Bergmann, F.; Zeitlinger, M. Protein binding in translational antimicrobial development-focus on interspecies differences. Antibiotics 2022, 11, 923. [Google Scholar] [CrossRef] [PubMed]
- Roberts, J.A.; Pea, F.; Lipma, J. The clinical relevance of plasma protein binding changes. Clin. Pharmacokinet. 2013, 52, 1–8. [Google Scholar] [CrossRef] [PubMed]
- Zhivkova, Z.; Doytchinova, I. Quantitative structure–-plasma protein binding relationships of acidic drugs. J. Pharm. Sci. 2012, 101, 4627–4641. [Google Scholar] [CrossRef]
- Zhu, X.W.; Sedykh, A.; Zhu, H.; Liu, S.S.; Tropsha, A. The use of pseudo-equilibrium constant affords improved QSAR models of human plasma protein binding. Pharm. Res. 2013, 30, 1790–1798. [Google Scholar] [CrossRef] [PubMed]
- Ingle, B.L.; Veber, B.C.; Nichols, J.W.; Tornero-Velez, R. Informing the human plasma protein binding of environmental chemicals by machine learning in the pharmaceutical space: Applicability domain and limits of predictability. J. Chem. Inf. Model. 2016, 56, 2243–2252. [Google Scholar] [CrossRef] [PubMed]
- Votano, J.R.; Parham, M.; Hall, L.M.; Hall, L.H.; Kier, L.B.; Oloff, S.; Tropsha, A. QSAR modeling of human serum protein binding with several modeling techniques utilizing structure-information representation. J. Med. Chem. 2006, 49, 7169–7181. [Google Scholar] [CrossRef] [PubMed]
- Sun, L.; Yang, H.; Li, J.; Wang, T.; Li, W.; Liu, G.; Tang, Y. In silico prediction of compounds binding to human plasma proteins by QSAR models. Chem. Med. Chem. 2018, 13, 572–581. [Google Scholar] [CrossRef]
- Zhang, R.R.; Grudzinksi, J.J.; Mehta, T.I.; Burnette, R.R.; Hernandez, R.; Clark, P.A.; Lubin, J.A.; Pinchuk, A.N.; Jeffrey, J.; Longino, M.; et al. In silico docking of alkylphosphocholine analogs to human serum albumin predicts partitioning and pharmacokinetics. Mol. Pharm. 2019, 16, 3350–3360. [Google Scholar] [CrossRef] [PubMed]
- Ciura, K.; Ulenberg, S.; Kapica, H.; Kawczak, P.; Belka, M.; Bączek, T. Drug affinity to human serum albumin prediction by retention of cetyltrimethylammonium bromide pseudostationary phase in micellar electrokinetic chromatography and chemically advanced template search descriptors. J. Pharm. Biomed. Anal. 2020, 188, 113423. [Google Scholar] [CrossRef] [PubMed]
- Chaturvedi, S.; Rashid, M.; Malik, M.Y.; Agarwal, A.; Singh, S.K.; Gayen, J.R.; Wahajuddin, M. Neuropharmacokinetics: A bridging tool between CNS drug development and therapeutic outcome. Drug Discov. Today 2019, 24, 1166–1175. [Google Scholar] [CrossRef] [PubMed]
- Cao, Y.; Ng, C. Absorption, distribution, and toxicity of per- and polyfluoroalkyl substances (PFAS) in the brain: A review. Env. Environ. Sci. Process Impacts 2021, 23, 1623–1640. [Google Scholar] [CrossRef] [PubMed]
- Chatterjee, S.; Deshpande, A.A.; Shen, H. Recent advances in the in vitro and in vivo methods to assess impact of P-glycoprotein and breast cancer resistance protein transporters in central nervous system drug disposition. Biopharm. Drug Dispos. 2023, 44, 7–25. [Google Scholar] [CrossRef] [PubMed]
- Summerfield, S.G.; Yates, J.W.T.; Fairman, D.A. Free drug theory–- no longer just a hypothesis? Pharm. Res. 2022, 9, 213–222. [Google Scholar] [CrossRef]
- Schmitt, M.V.; Reichel, A.; Liu, X.; Fricker, G.; Lienau, P. Extension of the mechanistic tissue distribution model of Rodgers and Rowland by systematic incorporation of lysosomal trapping: Impact on unbound partition coefficient and volume of distribution predictions in the rat. Drug Metab. Dispos. 2021, 49, 53–61. [Google Scholar] [CrossRef] [PubMed]
- Cen, Y.; Shan, Y.; Zhao, F.; Xu, X.; Nie, Z.; Zhang, J. Multiple drug transporters contribute to the brain transfer of levofloxacin. CNS Neurosci. Ther. 2023, 29, 445–457. [Google Scholar] [CrossRef] [PubMed]
- Hammarlund-Udenaes, M.; Fridén, M.; Syvänen, S.; Gupta, A. On the rate and extent of drug delivery to the brain. Pharm. Res. 2008, 25, 1737–1750. [Google Scholar] [CrossRef] [PubMed]
- Altendorfer-Kroath, T.; Schimek, D.; Eberl, A.; Rauter, G.; Ratzer, M.; Sinner, F.; Birngruber, T. Comparison of cerebral open flow microperfusion and microdialysis when sampling small lipophilic and small hydrophilic substances. J. Neurosci. Methods 2019, 311, 394–401. [Google Scholar] [CrossRef]
- Young, R.C.; Mitchell, R.C.; Brown, T.H.; Ganellin, C.R.; Griffiths, R.; Jones, M.; Rana, K.K.; Saunders, D.; Smith, I.R.; Sore, N.E. Development of a new physicochemical model for brain penetration and its application to the design of centrally acting H2 receptor histamine antagonists. J. Med. Chem. 1988, 31, 656–671. [Google Scholar] [CrossRef] [PubMed]
- Singh, M.; Divakaran, R.; Konda, L.S.K.; Kristam, R. A classification model for blood brain barrier penetration. J. Mol. Graph. Model. 2020, 96, 107516. [Google Scholar] [CrossRef] [PubMed]
- Lanevskij, K.; Dapkunas, J.; Juska, L.; Japertas, P.; Didziapetris, R. QSAR analysis of blood-brain distribution: The influence of plasma and brain tissue binding. J. Pharm. Sci. 2011, 100, 2060–2147. [Google Scholar] [CrossRef] [PubMed]
- Gupta, S.; Basant, N.; Singh, K.P. Qualitative and quantitative structure-activity relationship modelling for predicting blood-brain barrier permeability of structurally diverse chemicals. SAR QSAR Env. Environ. Res. 2015, 26, 95–124. [Google Scholar] [CrossRef]
- Chen, Y.; Zhu, Q.; Pan, J.; Yang, Y.; Wu, X. A prediction model for blood-brain barrier permeation and analysis on its parameter biologically. Comput. Methods Programs Biomed. 2009, 95, 280–287. [Google Scholar] [CrossRef]
- Vilar, S.; Chakrabarti, M.; Costanzi, S. Prediction of passive blood-brain partitioning: Straightforward and effective classification models based on in silico derived physicochemical descriptors. J. Mol. Graph. Model. 2010, 28, 899–903. [Google Scholar] [CrossRef]
- Shaker, B.; Yu, M.; Song, J.S.; Ahn, S.; Ryu, J.Y.; Oh, K.; Na, D. LightBBB: Computational prediction model of blood-brain-barrier penetration based on LightGBM. Bioinformatics 2021, 37, 1135–1139. [Google Scholar] [CrossRef] [PubMed]
- Yuan, Y.; Zheng, F.; Zhan, C. Improved Prediction of blood-brain barrier permeability through machine learning with combined use of molecular property-based descriptors and fingerprints. AAPS J. 2018, 20, 54. [Google Scholar] [CrossRef]
- Wang, Z.; Yang, H.; Wu, Z.; Wang, T.; Li, W.; Tang, Y.; Liu, G. In silico prediction of blood-brain barrier permeability of compounds by machine learning and resampling methods. Chem. Med. Chem. 2018, 13, 2189–2201. [Google Scholar] [CrossRef]
- Alsenan, S.; Al-Turaiki, I.; Hafez, A. A recurrent neural network model to predict blood-brain barrier permeability. Comput. Biol. Chem. 2020, 89, 107377. [Google Scholar] [CrossRef] [PubMed]
- Radan, M.; Djikic, T.; Obradovic, D.; Nikolic, K. Application of in vitro PAMPA technique and in silico computational methods for blood-brain barrier permeability prediction of novel CNS drug candidates. Eur. J. Pharm. Sci. 2022, 168, 106056. [Google Scholar] [CrossRef] [PubMed]
- Tong, X.; Wang, D.; Ding, X.; Tan, X.; Ren, Q.; Chen, G.; Rong, Y.; Xu, T.; Huang, J.; Jiang, H.; et al. Blood-brain barrier penetration prediction enhanced by uncertainty estimation. J. Cheminform 2022, 14, 44. [Google Scholar] [CrossRef] [PubMed]
- Liu, H.; Dong, K.; Zhang, W.; Summerfield, S.G.; Terstappen, G.C. Prediction of brain:blood unbound concentration ratios in CNS drug discovery employing in silico and in vitro model systems. Drug Discov. Today 2018, 23, 1357–1372. [Google Scholar] [CrossRef] [PubMed]
- Fridén, M.; Winiwarter, S.; Jerndal, G.; Bengtsson, O.; Wan, H.; Bredberg, U.; Hammarlund-Udenaes, M.; Antonsson, M. Structure-brain exposure relationships in rat and human using a novel data set of unbound drug concentrations in brain interstitial and cerebrospinal fluids. J. Med. Chem. 2009, 52, 6233–6243. [Google Scholar] [CrossRef] [PubMed]
- Chen, H.; Winiwarter, S.; Fridén, M.; Antonsson, M.; Engkvist, O. In silico prediction of unbound brain-to-plasma concentration ratio using machine learning algorithms. J. Mol. Graph. Model. 2011, 29, 985–995. [Google Scholar] [CrossRef]
- Varadharajan, S.; Winiwarter, S.; Carlsson, L.; Engkvist, O.; Anantha, A.; Kogej, T.; Markus Fridén Stålring, J.; Chen, H. Exploring in silico prediction of the unbound brain-to-plasma drug concentration ratio: Model validation, renewal, and interpretation. J. Pharm. Sci. 2015, 104, 1197–1206. [Google Scholar] [CrossRef]
- Spreafico, M.; Jacobson, M.P. In silico prediction of brain exposure: Drug free fraction, unbound brain to plasma concentration ratio and equilibrium half-life. Curr. Top. Med. Chem. 2013, 13, 813–820. [Google Scholar] [CrossRef]
- Loryan, I.; Sinha, V.; Mackie, C.; Van Peer, A.; Drinkenburg, W.H.; Vermeulen, A.; Heald, D.; Hammarlund-Udenaes, M.; Wassvik, C.M. Molecular properties determining unbound intracellular and extracellular brain exposure of CNS drug candidates. Mol. Pharm. 2015, 12, 520–532. [Google Scholar] [CrossRef]
- Dolgikh, E.; Watson, I.A.; Desai, P.V.; Sawada, G.A.; Morton, S.; Jones, T.M.; Raub, T.J. QSAR model of unbound brain-to-plasma partition coefficient, Kp,uu,brain: Incorporating p-glycoprotein efflux as a variable. J. Chem. Inf. Model. 2016, 56, 2225–2233. [Google Scholar] [CrossRef]
- Fridén, M.; Bergström, F.; Wan, H.; Rehngren, M.; Ahlin, G.; Hammarlund-Udenaes, M.; Bredberg, U. Measurement of unbound drug exposure in brain: Modeling of pH partitioning explains diverging results between the brain slice and brain homogenate methods. Drug Metab. Dispos. 2011, 39, 353–362. [Google Scholar] [CrossRef] [PubMed]
- Wan, H.; Rehngren, M.; Giordanetto, F.; Bergström, F.; Tunek, A. High-throughput screening of drug-brain tissue binding and in silico prediction for assessment of central nervous system drug delivery. J. Med. Chem. 2007, 50, 4606–4615. [Google Scholar] [CrossRef] [PubMed]
- Kosugi, Y.; Mizuno, K.; Santos, C.; Sato, S.; Hosea, N.; Zientek, M. Direct Comparison of the prediction of the unbound brain-to-plasma partitioning utilizing machine learning approach and mechanistic neuropharmacokinetic model. AAPS J. 2021, 23, 72. [Google Scholar] [CrossRef] [PubMed]
- Lawrenz, A.; Svensson, M.; Kato, M.; Dingley, K.H.; Elk, J.C.; Nie, Z.; Zou, Y.; Kaplan, Z.; Lagiakos, H.R.; Igawa, H.; et al. A computational physics-based approach to predict unbound brain-to-plasma partition coefficient, Kp,uu. J. Chem. Inf. Model. 2023, 63, 3786–3798. [Google Scholar] [CrossRef] [PubMed]
- Di, L.; Umland, J.P.; Chang, G.; Huang, Y.; Lin, Z.; Scott, D.O.; Troutman, M.D.; Liston, T.E. Species independence in brain tissue binding using brain homogenates. Drug Metab. Dispos. 2011, 39, 1270–1277. [Google Scholar] [CrossRef] [PubMed]
- Desai, P.V.; Sawada, G.A.; Watson, I.A.; Raub, T.J. Integration of in silico and in vitro tools for scaffold optimization during drug discovery: Predicting P-glycoprotein efflux. Mol. Pharm. 2013, 10, 1249–1261. [Google Scholar] [CrossRef] [PubMed]
- Gunaydin, H.; Weiss, M.M.; Sun, Y. De novo prediction of p-glycoprotein-mediated efflux liability for druglike compounds. ACS Med. Chem. Lett. 2012, 4, 108–112. [Google Scholar] [CrossRef] [PubMed]
- Chen, C.; Lee, M.; Weng, C.; Leong, M.K. Theoretical Prediction of the Complex P-glycoprotein substrate efflux based on the novel hierarchical support vector regression scheme. Molecules 2018, 23, 1820. [Google Scholar] [CrossRef] [PubMed]
- Lee, P.H.; Cucurull-Sanchez, L.; Lu, J.; Du, Y.J. Development of in silico models for human liver microsomal stability. J. Comput. Aided Mol. Des. 2007, 21, 665–673. [Google Scholar] [CrossRef]
- Sakiyama, Y.; Yuki, H.; Moriya, T.; Hattori, K.; Suzuki, M.; Shimada, K.; Honma, T. Predicting human liver microsomal stability with machine learning techniques. J. Mol. Graph. Model. 2008, 26, 907–915. [Google Scholar] [CrossRef]
- Gupta, R.R.; Gifford, E.M.; Liston, T.; Waller, C.L.; Hohman, M.; Bunin, B.A.; Ekins, S. Using open-source computational tools for predicting human metabolic stability and additional absorption, distribution, metabolism, excretion, and toxicity properties. Drug Metab. Dispos. 2010, 38, 2083–2090. [Google Scholar] [CrossRef]
- Sasahara, K.; Shibata, M.; Sasabe, H.; Suzuki, T.; Takeuchi, K.; Umehara, K.; Kashiyama, E. Predicting drug metabolism and pharmacokinetics features of in-house compounds by a hybrid machine-learning model. Drug Metab. Pharmacokinet. 2021, 39, 100395. [Google Scholar] [CrossRef] [PubMed]
- Sasahara, K.; Shibata, M.; Sasabe, H.; Suzuki, T.; Takeuchi, K.; Umehara, K.; Kashiyama, E. Feature importance of machine learning prediction models shows structurally active part and important physicochemical features in drug design. Drug Metab. Pharmacokinet. 2021, 39, 100401. [Google Scholar] [CrossRef]
- Liu, R.; Schyman, P.; Wallqvist, A. Critically assessing the predictive power of QSAR models for human liver microsomal stability. J. Chem. Inf. Model. 2015, 55, 1566–1575. [Google Scholar] [CrossRef] [PubMed]
- Siramshetty, V.B.; Shah, P.; Kerns, E.; Nguyen, K.; Yu, K.R.; Kabir, M.; Williams, J.; Neyra, J.; Southall, N.; Nguyễn, Ð.; et al. Retrospective assessment of rat liver microsomal stability at NCATS: Data and QSAR models. Sci. Rep. 2020, 10, 20713. [Google Scholar] [CrossRef] [PubMed]
- Li, L.; Lu, Z.; Liu, G.; Tang, Y.; Li, W. In silico prediction of human and rat liver microsomal stability via machine learning methods. Chem. Res. Toxicol. 2022, 35, 1614–1624. [Google Scholar] [CrossRef] [PubMed]
- Berellini, G.; Waters, N.J.; Lombardo, F. In silico prediction of total human plasma clearance. J. Chem. Inf. Model. 2012, 52, 2069–2078. [Google Scholar] [CrossRef] [PubMed]
- Yu, M.J. Predicting total clearance in humans from chemical structure. J. Chem. Inf. Model. 2010, 50, 1284–1295. [Google Scholar] [CrossRef] [PubMed]
- Lombardo, F.; Obach, R.S.; Varma, M.V.; Stringer, R.; Berellini, G. Clearance mechanism assignment and total clearance prediction in human based upon in silico models. J. Med. Chem. 2014, 57, 4397–4405. [Google Scholar] [CrossRef] [PubMed]
- Kosugi, Y.; Hosea, N. Prediction of oral pharmacokinetics using a combination of in silico descriptors and in vitro ADME properties. Mol. Pharm. 2021, 18, 1071–1079. [Google Scholar] [CrossRef]
- Ballante, F.; Kooistra, A.J.; Kampen, S.; de Graaf, C.; Carlsson, J. Structure-based virtual screening for ligands of G protein-coupled receptors: What can molecular docking do for you? Pharmacol. Rev. 2021, 73, 527–565. [Google Scholar] [CrossRef]
- Zanger, U.M.; Schwab, M. Cytochrome P450 enzymes in drug metabolism: Regulation of gene expression, enzyme activities, and impact of genetic variation. Pharmacol. Ther. 2013, 138, 103–141. [Google Scholar] [CrossRef] [PubMed]
- Zaretzki, J.; Rydberg, P.; Bergeron, C.; Bennett, K.P.; Olsen, L.; Curt M Breneman, C.M. RS-Predictor models augmented with SMARTCyp reactivities: Robust metabolic regioselectivity predictions for nine CYP isozymes. J. Chem. Inf. Model. 2012, 52, 1637–1659. [Google Scholar] [CrossRef]
- Skopalík, J.; Anzenbacher, P.; Otyepka, M. Flexibility of human cytochromes P450: Molecular dynamics reveals differences between CYPs 3A4, 2C9, and 2A6, which correlate with their substrate preferences. J. Phys. Chem. B 2008, 112, 8165–8173. [Google Scholar] [CrossRef] [PubMed]
- Sato, A.; Tanimura, N.; Honma, T.; Konagaya, A. Significance of data selection in deep learning for reliable binding mode prediction of ligands in the active site of CYP3A4. Chem. Pharm. Bull. 2019, 67, 1183–1190. [Google Scholar] [CrossRef] [PubMed]
- Muthusamy, R.; Bharatam, P.V. Molecular modeling studies on cytochrome P450-mediated drug metabolism. Curr. Drug Metab. 2021, 22, 683–697. [Google Scholar]
- Rowland Yeo, K.; Aarabi, M.; Jamei, M.; Rostami-Hodjegan, A. Modeling and predicting drug pharmacokinetics in patients with renal impairment. Expert. Rev. Clin. Pharmacol. 2011, 4, 261–274. [Google Scholar] [CrossRef]
- Huang, W.; Isoherranen, N. Novel Mechanistic PBPK Model to Predict Renal Clearance in Varying Stages of CKD by Incorporating Tubular Adaptation and Dynamic Passive Reabsorption. CPT Pharmacomet. Syst. Pharmacol. 2020, 9, 571–583. [Google Scholar] [CrossRef]
- Jansen, K.; Casellas, C.P.; Groenink, L.; Wever, K.E.; Masereeuw, R. Humans are animals, but are animals human enough? A systematic review and meta-analysis on interspecies differences in renal drug clearance. Drug Discov. Today 2020, 25, 706–717. [Google Scholar] [CrossRef]
- Doddareddy, M.R.; Cho, Y.S.; Koh, H.Y.; Kim, D.H.; Pae, A.N. In silico renal clearance model using classical Volsurf approach. J. Chem. Inf. Model. 2006, 46, 312–320. [Google Scholar] [CrossRef]
- Chen, J.; Yang, H.; Zhu, L.; Wu, Z.; Li, W.; Tang, Y.; Liu, G. In silico prediction of human renal clearance of compounds using quantitative structure-pharmacokinetic relationship models. Chem. Res. Toxicol. 2020, 33, 640–650. [Google Scholar] [CrossRef] [PubMed]
- Dave, R.A.; Morris, M.E. Quantitative structure-pharmacokinetic relationships for the prediction of renal clearance in humans. Drug Metab. Dispos. 2015, 43, 73–81. [Google Scholar] [CrossRef] [PubMed]
- Kusama, M.; Toshimoto, K.; Kazuya Maeda, K.; Hirai, Y.; Imai, S.; Chiba, K.; Akiyama, Y.; Sugiyama, Y. In silico classification of major clearance pathways of drugs with their physiochemical parameters. Drug Metab. Dispos. 2010, 38, 1362–1370. [Google Scholar] [CrossRef] [PubMed]
- Toshimoto, K.; Wakayama, N.; Kusama, M.; Maeda, K.; Sugiyama, Y.; Akiyama, Y. In silico prediction of major drug clearance pathways by support vector machines with feature-selected descriptors. Drug Metab. Dispos. 2014, 42, 1811–1819. [Google Scholar] [CrossRef] [PubMed]
- Wakayama, N.; Toshimoto, K.; Maeda, K.; Hotta, S.; Ishida, T.; Akiyama, Y.; Sugiyama, Y. In silico prediction of major clearance pathways of drugs among 9 routes with two-step support vector machines. Pharm. Res. 2018, 35, 197. [Google Scholar] [CrossRef]
- Ose, A.; Toshimoto, K.; Ikeda, K.; Maeda, K.; Yoshida, S.; Yamashita, F.; Hashida, M.; Ishida, T.; Akiyama, Y.; Sugiyama, Y. Development of a support vector machine-based system to predict whether a compound is a substrate of a given drug transporter using its chemical structure. J. Pharm. Sci. 2016, 105, 2222–2230. [Google Scholar] [CrossRef]
- Wang, M.W.H.; Goodman, J.M.; Allen, T.E.H. Machine learning in predictive toxicology: Recent applications and future directions for classification models. Chem. Res. Toxicol. 2021, 34, 217–239. [Google Scholar] [CrossRef]
- Ogura, K.; Sato, T.; Yuki, H.; Honma, T. Support Vector Machine model for hERG inhibitory activities based on the integrated hERG database using descriptor selection by NSGA-II. Sci. Rep. 2019, 9, 12220. [Google Scholar] [CrossRef]
- Alves, V.M.; Auerbach, S.S.; Kleinstreuer, N.; Rooney, J.P.; Muratov, E.N.; Rusyn, I.; Tropsha, A.; Schmitt, C. Curated data in-trustworthy in silico models out: The impact of data quality on the reliability of artificial intelligence models as alternatives to animal testing. Altern. Lab. Anim. 2021, 49, 73–82. [Google Scholar] [CrossRef]
- Hu, Y.; Ren, Q.; Liu, X.; Gao, L.; Xiao, L.; Wenying Yu, W. In silico prediction of human organ toxicity via artificial intelligence methods. Chem. Res. Toxicol. 2023, 36, 1044–1054. [Google Scholar] [CrossRef]
- Hemmerich, J.; Gerhard F Ecker, G.F. In silico toxicology: From structure-activity relationships towards deep learning and adverse outcome pathways. Wiley Interdiscip. Rev. Comput. Mol. Sci. 2020, 10, e1475. [Google Scholar] [CrossRef] [PubMed]
- Leedale, J.; Sharkey, K.J.; Colley, H.E.; Norton, Á.M.; Peeney, D.; Mason, C.L.; Sathish, J.G.; Murdoch, C.; Sharma, P.; Webb, S.D. A combined in vitro/in silico approach to identifying off-target receptor toxicity. iScience 2018, 4, 84–96. [Google Scholar] [CrossRef] [PubMed]
- Xiong, G.; Wu, Z.; Yi, J.; Fu, L.; Yang, Z.; Hsieh, C.; Yin, M.; Zeng, X.; Wu, C.; Lu, A.; et al. ADMETlab 2.0: An integrated online platform for accurate and comprehensive predictions of ADMET properties. Nucleic Acids Res. 2021, 49, W5–W14. [Google Scholar] [CrossRef] [PubMed]
- Dong, J.; Wang, N.N.; Yao, Z.J.; Zhang, L.; Cheng, Y.; Ouyang, D.; Lu, A.P.; Cao, D.S. ADMETlab: A platform for systematic ADMET evaluation based on a comprehensively collected ADMET database. J. Cheminform 2018, 10, 29. [Google Scholar] [CrossRef]
- Kawashima, H.; Watanabe, R.; Esaki, T.; Kuroda, M.; Nagao, C.; Natsume-Kitatani, Y.; Ohashi, R.; Komura, H.; Mizuguchi, K. DruMAP: A novel drug metabolism and pharmacokinetics analysis platform. J. Med. Chem. 2023, 66, 9697–9709. [Google Scholar] [CrossRef]
- Esaki, T.; Ohashi, R.; Watanabe, R.; Natsume-Kitatani, Y.; Kawashima, H.; Nagao, C.; Komura, H.; Mizuguchi, K. Constructing an in silico three-class predictor of human intestinal absorption with Caco-2 permeability and dried-DMSO solubility. J. Pharm. Sci. 2019, 108, 3630–3639. [Google Scholar] [CrossRef]
- Watanabe, R.; Esaki, T.; Kawashima, H.; Natsume-Kitatani, Y.; Nagao, C.; Ohashi, R.; Mizuguchi, K. Predicting fraction unbound in human plasma from chemical structure: Improved accuracy in the low value ranges. Mol. Pharm. 2018, 15, 5302–5311. [Google Scholar] [CrossRef]
- Esaki, T.; Ohashi, R.; Watanabe, R.; Natsume-Kitatani, Y.; Kawashima, H.; Nagao, C.; Mizuguchi, K. Computational model to predict the fraction of unbound drug in the brain. J. Chem. Inf. Model. 2019, 59, 3251–3261. [Google Scholar] [CrossRef]
- Watanabe, R.; Esaki, T.; Ohashi, R.; Kuroda, M.; Kawashima, H.; Komura, H.; Natsume-Kitatani, Y.; Mizuguchi, K. Development of an in silico prediction model for P-glycoprotein efflux potential in brain capillary endothelial cells toward the prediction of brain penetration. J. Med. Chem. 2021, 64, 2725–2738. [Google Scholar] [CrossRef]
- Esaki, T.; Watanabe, R.; Kawashima, H.; Ohashi, R.; Natsume-Kitatani, Y.; Nagao, C.; Mizuguchi, K. Data curation can improve the prediction accuracy of metabolic intrinsic clearance. Mol. Inf. Inform. 2019, 38, e1800086. [Google Scholar] [CrossRef]
- Watanabe, R.; Ohashi, R.; Esaki, T.; Kawashima, H.; Natsume-Kitatani, Y.; Nagao, C.; Mizuguchi, K. Development of an in silico prediction system of human renal excretion and clearance from chemical structure information incorporating fraction unbound in plasma as a descriptor. Sci. Rep. 2019, 9, 18782. [Google Scholar] [CrossRef]
- Ohashi, R.; Watanabe, R.; Esaki, T.; Taniguchi, T.; Torimoto-Katori, N.; Watanabe, T.; Ogasawara, Y.; Takahashi, T.; Tsukimoto, M.; Mizuguchi, K. Development of simplified in vitro P-Glycoprotein substrate assay and in silico prediction models to evaluate transport potential of P-glycoprotein. Mol. Pharm. 2019, 16, 1851–1863. [Google Scholar] [CrossRef] [PubMed]
- Kuroda, M.; Watanabe, R.; Esaki, T.; Kawashima, H.; Ohashi, R.; Sato, T.; Honma, T.; Komura, H.; Mizuguchi, K. Utilizing public and private sector data to build better machine learning models for the prediction of pharmacokinetic parameters. Drug Discov. Today 2022, 27, 103339. [Google Scholar] [CrossRef] [PubMed]
- Schneckener, S.; Grimbs, S.; Hey, J.; Menz, S.; Osmers, M.; Schaper, S.; Hillisch, A.; Göller, A.H. Prediction of oral bioavailability in rats: Transferring insights from in vitro correlations to (Deep) machine learning models using in silico model outputs and chemical structure parameters. J. Chem. Inf. Model. 2019, 59, 4893–4905. [Google Scholar] [CrossRef]
- Kamiya, Y.; Handa, K.; Miura, T.; Yanagi, M.; Shigeta, K.; Hina, S.; Shimizu, M.; Kitajima, M.; Shono, F.; Funatsu, K.; et al. In silico prediction of input parameters for simplified physiologically based pharmacokinetic models for estimating plasma, liver, and kidney exposures in rats after oral doses of 246 disparate chemicals. Chem. Res. Toxicol. 2021, 34, 507–513. [Google Scholar] [CrossRef] [PubMed]
- Miljković, F.; Martinsson, A.; Obrezanova, O.; Williamson, B.; Johnson, M.; Sykes, A.; Bender, A.; Greene, N. Machine learning models for human in vivo pharmacokinetic parameters with in-house validation. Mol. Pharm. 2021, 18, 4520–4530. [Google Scholar] [CrossRef] [PubMed]
- Handa, K.; Wright, P.; Yoshimura, S.; Kageyama, M.; Iijima, T.; Bender, A. Prediction of compound plasma concentration-time profiles in mice using random forest. Mol. Pharm. 2023, 20, 3060–3072. [Google Scholar] [CrossRef]
- Iwata, H.; Matsuo, T.; Mamada, H.; Motomura, T.; Matsushita, M.; Fujiwara, T.; Maeda, K.; Handa, K. Predicting total drug clearance and volumes of distribution using the machine learning-mediated multimodal method through the imputation of various nonclinical data. J. Chem. Inf. Model. 2022, 62, 4057–4065. [Google Scholar] [CrossRef] [PubMed]

| Assay | Dataset | Type of Model | Algorithms | Predictive Performance | Ref. | ||
|---|---|---|---|---|---|---|---|
| No of cpds | Source | Parameters | |||||
| Solubility | 483 | AQUASOL and SRC databases | Aqueous solubility | Two-classification model | Cart classification model | Sensitivity = 0.823, selectivity = 0.879 | [27] |
| Solubility | 11,780–22,209 | In-house assay data | Kinetic solubility | Two-classification model | RF, GCNN | AUC-ROC = 0.87–0.90, Sensitivity = 0.63–0.71, Specificity = 0.90–0.91 | [28] |
| Solubility | 12,674 | Two public databases | Aqueous solubility | Combination of two-classification and regression models | Gradient boosting and recursive RF | R2 = 0.87 for consensus model Sensitivity = 0.80, specificity = 0.96 | [29] |
| Permeability | 207 | In-house cpds measured | Caco-2 cells | QSAR | Multivariant linear regression | R = 0.76 | [30] |
| Permeability | 130 | Literature | Caco-2 cells | QSAR | Innovative machine learning-based HSVR | R2 = 0.91 | [31] |
| Permeability | 386 | Marketed drugs | MDCK cells | QSAR | PLS, SVM | AUC = 0.84 for PLS, 0.81 for SVM | [32] |
| Permeability | 74 | Discovery cpds | Rat intestinal permeability | QSAR | HSVR | R2 = 0.93 | [33] |
| Permeability | 71 | Drugs peptide mimic compounds | PAMPA | QSAR | Regression analysis | R2 = 0.76 | [34] |
| Permeability | 182 | Literature | PAPMA | QSAR | PLS, HSVR | Q2 = 0.88 for HSVR and 0.61 for PLS | [35] |
| Permeability | >6500 | Drugs and drug-like compounds | PAMPA | Four-classifier models | Graph convolutional neural network | Sensitivity = 0.74 specificity = 0.82 | [24] |
| Permeability | 2406–16,624 | In-house | PAMPA | Two-classifier model | RF, GCNN | AUC-ROC = 0.85–0.86, Sensitivity = 0.83–0.84, Specificity = 0.64–0.78 | [28] |
| Assay | Dataset | Type of Model | Algorithms | Predictive Performance | Ref. | ||
|---|---|---|---|---|---|---|---|
| No of cpds | Source | Parameter | |||||
| HIA | 86 | Drugs and drug-like cpds | Fa | QSAR | GRNN, probabilistic neutral network | RMS = 22.8% for GRNN, | [42] |
| HIA | 455 | Drugs and drug-like cpds | Fa | QSAR, Two-classifier model | Genetic function approximation, recursive partitioning techniques | R = 0.84, 95.9% poorly absorbed compounds and 96.1% well-absorbed compounds | [43] |
| HIA | 141 | ChEMBL, research and serotonin database | Fa | Two-classifier model, QSAR | Hierarchical combination of classification and regression | Accuracy = 0.765, precision = 0.782 R2 = 0.379 | [44] |
| HIA | 932 | Several research and FDA drug databases | Fa | Two-classifier model | Cart classification model | Sensitivity = 0.745, specificity = 0.865 | [27] |
| HIA | 578 | Hou’s research | Fa | Two-classification model | SVM | Sensitivity = 0.998, specificity = 0.859–0.897 | [41] |
| HIA | 225 | Zhao’s research | Fa | Classification models | Gaussian process classification, RF, SVM | Gaussian process classier RF, SVM κ = 0.42–0.58 | [45] |
| HIA | 578 | Research | HIA | SAR-based SAR model, QSAR | Linear SAR and ensemble learning-based SAR modeling | Qualitative SAR > 99%, QSAR: R2 > 0.91 | [46] |
| Assay | Data Set | Type of Model | Algorithms | Predictive Performance | Ref. | ||
|---|---|---|---|---|---|---|---|
| No of cpds | Source | Parameter | |||||
| Human plasma protein binding | 117 | Data from the literature | Unbound fraction | QSAR | PLS | Q2 = 0.69 | [54] |
| 132 | Obach’s database | Unbound fraction | QSAR | Stepwise linear regression | R2 = 0.771, Q2 = 0.737 | [57] | |
| 1045 | Drugs | Unbound fraction | QSAR | RF, SVM, κ-nearest neighbor | MAE = 0.10–0.18 | [59] | |
| 1242 | Drugs or drug-like cpds from DrugBank, etc. | Bound fraction | QSAR | RF, SVM, κ-nearest neighbor | R2 = 0.67 | [58] | |
| 967 | DrugBank, etc. | Bound fraction | QSAR | RF, SVM, κ-NN, multi-layer NN | MAE = 0.129–0.178 | [61] | |
| 1008 | Experimental data | Bound fraction | QSAR | MLR, artificial neural network, SVM | MAE = 7.6–18.3, R2 = 0.61–0.90 | [60] | |
| Assay | Data Set | Type of Model | Algorithm, Descriptors or Equation of Model | Predictive Performance | Ref. | |
|---|---|---|---|---|---|---|
| No of cpds | Source | |||||
| BBB permeation | 470 | Experimental data under steady-state condition | QSAR | nonlinear least-squares minimization with logP, pKa, plasma protein binding | R2 = 0.52 | [74] |
| BBB permeation | 362 | In vivo data from some research | QSAR | Nonlinear model with XlogP, TPSA, Dipole | R2 = 0.926 | [75] |
| BBB permeation | 120 | In vivo data | QSAR | Three layered feedforward NN | R2 = 0.67 | [76] |
| BBB permeation | 307 | In vivo data from some publications | QSAR | Model 1: log BB > 0.3 log BB class = 0.5159 × log P(o/w) − 0.0277 × TPSA − 0.3462 Model 2: log BB < −1 log BB = 0.2289 × logP(o/w) − 0.0326 × TPSA−0.5671 × (a.acid + a.base) + 2.3420 | Good classification > 0.80 | [77] |
| BBB permeation | 1147 | The literature and world drug index dataset | Two-classification model | RF, MLP, and SMO (sequential minimal optimization) | Consensus model Accuracy = 0.88, selectivity = 0.88, specificity = 0.88 | [73] |
| BBB permeation | 7162 | 7 studies | Two-classification model | Light gradient-boosting machine | Selectivity = 0.90, specificity = 0.94 | [78] |
| BBB permeation | 1990 | In vivo data from some research | Two-classification model | SVM with molecular property-based descriptors including 1D, 2D and 3D descriptors and fingerprints | Selectivity = 0.962, specificity = 0.944 and Q2 = 0.957 | [79] |
| BBB permeation | 2358 | In vivo data from some research | Two-classification model | SVM with MACCS fingerprints | Accuracy = 0.966 | [80] |
| BBB permeation | 3961 | The literature | Two-classification model | Relational GCN | Accuracy = 0.872, sensitivity = 0.919, specificity = 0.763 | [81] |
| BBB permeation | 2342 | The literature | Two-classification model | Deep-learning-based recurrent neural network model | Accuracy= 0.965, selectivity = 0.949, specificity = 0.981 | [82] |
| BBB permeation | 18 | PAMPA | QSAR | Stepwise MLR, PLS, SVM | R2 = 0.86 for MLR, 0.73 for PLS, 0.81 for SVM | [83] |
| Assay | Dataset | Type of Prediction Models | Algorithms | Predictive Performance | Ref. | ||
|---|---|---|---|---|---|---|---|
| No of cpds | Source of cpds | Parameter | |||||
| Human liver microsome | 14,557 | Cpds from various laboratories within company | CLint | Two-classification model | RF, Bayesian | Prediction accuracy = 0.80 | [99] |
| Human liver microsome | 1952 | Proprietary cpds | CLint | Two-classification model | RF, SVM | Sensitivity > 0.9, specificity > 0.6 | [100] |
| Human liver microsome | 49,968 | Synthesized cpds by in-house projects | CLint | Three-classification model | RF, SVM C5.0 decision tree | Sensitivity = 0.57, specificity = 0.91 | [101] |
| Human liver microsome | 26,138 | Proprietary cpds | CLint | Two-classification model | RF, XGB, GCN | Accuracy = 0.799 | [102,103] |
| Human liver microsome | 4012 | ChEMBL | t1/2 | QSAR Classification model | RF, variable nearest neighbor | Sensitivity = 0.78, 0.73, specificity =0.85, 0.88 | [104] |
| Rat liver microsome | >24,000 | Cpds from > 250 projects at NCATs | t1/2 | Two-classification model | RF, deep neural network, GCNN | Sensitivity = 0.86, specificity = 0.77 | [105] |
| Human and rat Liver microsome | 4771 for humans, 2512 for rats | ChEMBL | t1/2 | Two-classification model | RF, XGBoost, neural network, κ-nearest neighbor | AUC = 0.86 for human, AUC = 0.84 for rat | [106] |
| Parameters | Data Set | Type of Model | Algorithms | Predictive Performance | Ref. | |
|---|---|---|---|---|---|---|
| No of cpds | Source | |||||
| CLr | 130 | Marketed drugs | QSAR | PLS | R2 = 0.844 by Volsurf; R2 = 0.720 by Molcom-Z | [120] |
| CLr | 250 | Drugs and drug-like compounds | Two-classify-cation model (distinguish GNetR and GNetS) | ANN, classification tree, κ-nearest neighbor, RF, SVM | AUC = 0.66–0.68 | [121] |
| CLr | 636 | Drugs and drug-like compounds | Global model | MLR and RF | R2 = 0.21–0.36 | [121] |
| CLr | 265–371 | Drugs and drug-like compounds | Local model (GNetS, GNetR) | MLR and RF | R2 = 0.45–0.54 for GNetS, R2 = 0.48–0.76 for GNetR | [121] |
| CLr | 382 | Drugs and drug-like compounds | QSAR | StepwiseMLR | R2 = 0.79 for net reabsorption clearance | [122] |
| Renal elimination | 141 (Renal:41) | Approved drugs | Two-classification model | Rectangular approach (3-dimentional analysis with fu,p, MW and log D) | Recall = 0.90 | [123] |
| Renal elimination | 141 (Renal:41) | Approved drugs | Two-classification model | Rectangular approach, SVM | Recall = 0.71–0.90 | [124] |
| Renal elimination | 419 | Drugs | Two-classification model | SVM, single-step approach, two-step approach with subset clustering | Recall = 0.85 | [125] |
| Pharmacokinetic Items | Dataset (No of cpds) | Type of Models | Algorithms | Predictive Performance | Ref |
|---|---|---|---|---|---|
| Solubility | 367 | Two-classification | Linear SVM | Accuracy: 0.811, Kappa: 0.628 | [136] |
| Permeability | 3532 | Two-classification | Linear SVM | Accuracy: 0.824, Kappa: 0.401 | [136] |
| Intestinal absorption | 946 | Three-classification | Linear SVM | Accuracy: 0.836, Kappa: 0.560 | [136] |
| Plasma protein binding | 2738 | Regression | RF | R2 = 0.691 | [137] |
| Brain homogenate | 253 | Regression | Gradient boosting | R2 = 0.630 | [138] |
| P-glycoprotein: net efflux ratio | 28–46 | Confusion matrix model | Gradient boosting | Kapp = 0.45 | [139] |
| Metabolic stability | 4685 | Three-classification | Radial SVM | Accuracy: 0.771 Kappa: 0.588 | [140] |
| Urinary excretion | 411 | Two-classification | RF | Balanced accuracy: 0.74 | [141] |
| Renal clearance | 401 | Two-step prediction system: three-classification and regression model | RF | R2 for reabsorption type: 0.47, intermediate type: 0.68, secretion type: 0.46 | [141] |
Disclaimer/Publisher’s Note: The statements, opinions and data contained in all publications are solely those of the individual author(s) and contributor(s) and not of MDPI and/or the editor(s). MDPI and/or the editor(s) disclaim responsibility for any injury to people or property resulting from any ideas, methods, instructions or products referred to in the content. |
© 2023 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Komura, H.; Watanabe, R.; Mizuguchi, K. The Trends and Future Prospective of In Silico Models from the Viewpoint of ADME Evaluation in Drug Discovery. Pharmaceutics 2023, 15, 2619. https://doi.org/10.3390/pharmaceutics15112619
Komura H, Watanabe R, Mizuguchi K. The Trends and Future Prospective of In Silico Models from the Viewpoint of ADME Evaluation in Drug Discovery. Pharmaceutics. 2023; 15(11):2619. https://doi.org/10.3390/pharmaceutics15112619
Chicago/Turabian StyleKomura, Hiroshi, Reiko Watanabe, and Kenji Mizuguchi. 2023. "The Trends and Future Prospective of In Silico Models from the Viewpoint of ADME Evaluation in Drug Discovery" Pharmaceutics 15, no. 11: 2619. https://doi.org/10.3390/pharmaceutics15112619
APA StyleKomura, H., Watanabe, R., & Mizuguchi, K. (2023). The Trends and Future Prospective of In Silico Models from the Viewpoint of ADME Evaluation in Drug Discovery. Pharmaceutics, 15(11), 2619. https://doi.org/10.3390/pharmaceutics15112619