Integrating ISA and Part-of Domain Knowledge into Process Model Discovery
Abstract
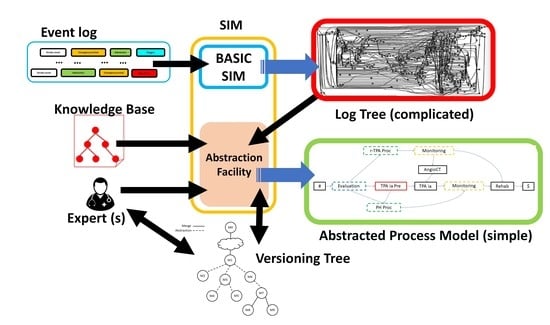
:1. Introduction
- (i)
- The possibility of giving domain experts/analysts an active role in the discovery of the process model.
- (ii)
- The possibility of adopting, besides “syntactic” forms of abstraction, also “semantic” (our terminology (specifically, we term “syntactic” all those forms of abstraction that are independent of the specific activities (but they consider, e.g., their number and/or their order); on the other hand, we term “semantic” those abstractions that depend on the specific activities (so that they require some form of—explicit or implicit—semantic knowledge about the activities in the domain))) ones.
2. Related Work
3. Preliminaries
3.1. SIM: Generalities
3.2. Representation Formalism (Process Model)
3.3. Query Language and Pattern Retrieval Facility
3.4. Merge Operations
4. A Model for the Domain Knowledge
- ISA relationships are (subtype–supertype) subsumption relations between classes (of entities; in our case, of activities): a class of activities A is a superclass of B when A’s specification implies B’s specification. For instance, in the knowledge base in Figure 4, intravenous thrombolysis (r-TPA Proc), intra-arterial thrombolysis (TPA ia Proc), and pharmacological therapy (PH Proc) are subclasses of Treatment.
- Part-of relationships are partonomic (i.e., part-whole) relations between classes; in the case of activities, they relate a class A with the classes C1,…,Cn composing it, modeling the decomposition of composite activities into the sub-activities composing them. For instance, in the knowledge base in Figure 4, Stroke_Management is composed of four (sub-)activities: Evaluation_L1, Treatment, Monitoring_L1, and Rehab_L1 (rehabilitation).
- “ISA nodes”, i.e., nodes N, whose sons in the KB hierarchy are in an ISA relationship with N;
- “Part-Of nodes”, i.e., nodes N, whose sons in the KB hierarchy are in a part-of relationship with N;
- “ground nodes”, i.e., nodes that have no sons in the KB hierarchy (representing the ground non-decomposable activities appearing in the input traces in the log).
- An evaluation of the patient’s condition (Evaluation in the KB in Figure 4, further abstracted as Evaluation_L1 at level 1), obtained through tests and instrumental exams, such as blood test and computerized tomography (BT and CT in the KB, respectively) and a neurological evaluation (EVAL).
- The treatment (Treatment in the KB in Figure 4) can consist of intravenous thrombolysis (r-TPA Proc), intra-arterial thrombolysis (TPA ia Proc), or pharmacological therapy (PH Proc). In turn, r-TPA Proc begins with a preparation phase (r-TPA Pre), composed of magnetic resonance with contrast (MR DW) and electrocardiogram (ECG) and continues with r-TPA drug administration (r-TPA). Similarly, TPA ia Proc starts with TPA ia Pre, composed of some preliminary steps (acetylsalicylic acid administration (ASA) and AngioCT), and continues with the TPA ia treatment itself. PH Proc, instead, starts with a preparatory phase (PH Pre), composed of tests such as ECG and magnetic resonance (MR). ASA (further abstracted as ASA_L3 at level 3) and anti-hypertensive drugs (Anti-HP) are then administered.
- A monitoring phase (Monitoring, further abstracted as Monitoring_L1 at level 1). Monitoring is usually performed through tests such as ECG (further abstracted as ECG_L3 at level 3), CT, and the administration of ASA.
- A rehabilitation phase (Rehab, further abstracted as Rehab_L1 at level 1).
5. Knowledge-Based Abstraction Operations
5.1. Main Issues
- Interactive vs. automatic application of the abstraction;
- Activity-based abstractions vs. level-based abstractions.
5.2. Automatic Abstraction Operators
- KB: the starting node of the ontological KB;
- AN: the node the user wishes to abstract;
- PM: the current process model (represented as a graph), which needs to be abstracted, in regard to the instances of node AN;
- AbstrST: a table maintaining the information of what KB nodes have already been considered for abstraction.
| Algorithm 1: pseudocode of automatic activity-based abstraction algorithm. |
| 1: AutomaticActAbstract (KB, AN, PM, AbstrST) 2: if (not LegalAbstraction? (KB, AN, AbstrST)) then 3: signal warning 4: else 5: PerformAutAbstraction (KB, AN, PM, AbstrST) 6: endif |
| Algorithm 2: pseudocode of the recursive automatic abstraction algorithm. |
| 1: PerformAutAbstraction (KB, AN, PM, AbstrST) 2: if (not Abstracted? (AN, AbstrST) and not GroundNode? (KB, AN)) then 3: if IsaNode? (KB, AN) then 4: for each Node in GetSons (KB, AN) do 5: PerformAutAbstraction (KB, Node, PM, AbstrST) 6: Substitute (Find (Node, PM), AN, PM) 7: end for 8: Add (AN, AbstrST) 9: else 10: if PartOfNode? (KB, AN) then 11: for each Node in GetSons (KB, AN) do 12: PerformAutAbstraction (KB, Node, PM, AbstrST) 13: end for 14: Substitute (Exec (AN, PM), AN, PM) 15: Add (AN, AbstrST) 16: end if 17: end if 18: end if |
5.2.1. Automatic Abstraction in Our Running Example
5.3. Interactive Abstraction Operators
- KB: the starting node of the ontological KB;
- AN: the node of KB the user wishes to abstract;
- PM: the current process model, which needs to be abstracted, in regard to the instances of node AN;
- AbstrST: the abstraction symbol table, which keeps track of what KB nodes, have already been considered for abstraction in PM.
| Algorithm 3: pseudocode of the interactive activity-based abstraction algorithm. |
| 1: InteractiveActAbstract (KB, AN, PM, AbstrST) 2: D ← DistanceGround (KB, AN) 3: for L ← D-1 to 0 do 4: Nodes ← GetNodesLevel (KB, AN, L) 5: Paths ← {} 6: for each N in Nodes do 7: if (not GroundNode? (KB, N) and not Abstracted? (N, AbstrST)) then 8: if IsaNode? (KB, N) then 9: for each CN in GetSons (KB, N) do 10: Substitute (Find (CN, PM), N, PM) 11: end for 12: Add (N, AbstrST) 13: else 14: if PartOfNode? (KB, N) then 15: Paths ← Paths ⋃ <Exec (N, PM), N> 16: Add (N, AbstrST) 17: end if 18: end if 19: end if 20: end for 21: if (not IsEmpty? (Paths)) then 22: PartitionSet ← Partition (Paths) 23: for each Set in PartitionSet do 24: SolveAndAbstract(Set, PM) 25: end for 26: end if 27: end for |
- T: a set of intersecting paths that needs to be abstracted; each element is a pair <P, AN>, where P is a path of the process model PM (see below), and AN is the part-of node, in which P may be abstracted;
- PM: the current process model that needs to be abstracted.
| Algorithm 4: pseudocode of the conflict resolution and abstraction algorithm. |
| 1: SolveAndAbstract (T, PM) 2: A ← AskAbstractions (T, PM) 3: PathsToKeep ← AskPaths (A, PM) 4: NodesToDelete ← {} 5: ArcsToDelete ← {} 6: for each <X, AN> in A do 7: N ← CreateNode (AN, PM) 8: CreateArcs (N, GetInArcs (X, PM), GetOutArcs (X, PM)) 9: NodesToDelete ← NodesToDelete ⋃ GetPathNodes (X) 10: ArcsToDelete ← ArcsToDelete ∪ GetInArcs (X,PM) ∪ GetOutArcs (X, PM) ⋃ GetPathArcs (X) 11: end for 12: for each P in PathsToKeep do 13: NodesToDelete ← NodesToDelete—GetPathNodes (P) 14: ArcsToDelete ← ArcsToDelete—GetPathArcs (P) 15: end for 16: Delete (PM, NodesToDelete, ArcsToDelete) |
6. Interactive Process-Model Discovery through Merge and Abstraction
| Algorithm 5:GenerateModel pseudo-code. |
| 1: GenerateModel (VerTree, L, KB) Output: Node 2: CurNode ← Root (VerTree) 3: Operation ← AskOp (CurNode) 4: while Operation ≠ “approve” do 5: switch Operation do 6: case “analyze”: 7: … query answering operations … 8: case “merge”: 9: MergeParameters ← AskMergeParameters (CurNode) 10: NewModel ← ExecuteMerge (CurNode.Model, MergeParameters) 11: NewNode ← AppendSon (CurNode, NewModel, CurNode.AbstrST) 12: CurNode ← NewNode 13: case “abstract”: 14: AbstractionModality ← AskModality () 15: switch AbstractionModality do 16: case “automatic_activity”: 17: Activity ← AskActivity (KB) 18: NewModel ← AutomaticActAbstract (KB, Activity, CurNode.Model, CurNode.AbstrST) 19: NewAbstrST ← CurNode.AbstrST ∪ {Activity} 20: case “automatic_level”: 21: Level ← AskLevel (KB) 22: Activities ← GetActivities (KB, Level) 23: NewModel ← AutomaticLevAbstract (KB, Activities, CurNode.Model, CurNode.AbstrST) 24: NewAbstrST ← CurNode.AbstrST ∪ {Activities} 25: case “interactive_activity”: 26: Activity ← AskAction (KB) 27: NewModel ← InteractiveActAbstract (KB, Activity, CurNode.Model, CurNode.AbstrST) 28: NewAbstrST ← CurNode.AbstrST ∪ {Activity} 29: case “interactive_level”: 30: Level ← AskLevel (KB) 31: Activities ← GetActivities (KB, Level) 32: NewModel ← InteractiveLevAbstract (KB, Level, CurNode.Model, CurNode.AbstrST) 33: NewAbstrST ← CurNode.AbstrST ∪ {Activities} 34: end switch 35: NewNode ← AppendSon(CurNode, NewModel, NewAbstrST) 36: CurNode ← NewNode 37: case “back”: 38: CurNode ← AskCur (VerTree) 39: end switch 40: Operation ← AskOp (CurNode) 41: end while 42: return CurNode |
7. Experimental Work
8. Conclusions
Author Contributions
Funding
Data Availability Statement
Conflicts of Interest
Appendix A. Experimental Comparison




| Process Model | Number of Nodes | Number of Edges |
|---|---|---|
| Alpha | 14 | 50 |
| Fuzzy | 14 | 22 |
| Heuristic | 14 | 22 |
| ILP | 14 | 42 |
| SIM | 11 | 14 |
References
- Van der Aalst, W.M.P. Data Mining. In Process Mining: Data Science in Action; Springer: Berlin/Heidelberg, Germany, 2016; pp. 89–121. [Google Scholar] [CrossRef]
- Van der Aalst, W.M.P.; Rubin, V.; Verbeek, H.M.W.; van Dongen, B.F.; Kindler, E.; Günther, C.W. Process mining: A two-step approach to balance between underfitting and overfitting. Softw. Syst. Modeling 2010, 9, 87. [Google Scholar] [CrossRef] [Green Version]
- Bottrighi, A.; Canensi, L.; Leonardi, G.; Montani, S.; Terenziani, P. Interactive mining and retrieval from process traces. Expert Syst. Appl. 2018, 110, 62–79. [Google Scholar] [CrossRef]
- Buijs, J.; van Dongen, B.; van der Aalst, W.M.P. On the role of fitness, precision, generalization and simplicity in process discovery. In Proceedings of the On the Move to Meaningful Internet Systems: OTM 2012, Rome, Italy, 10–14 September 2012; Springer: Berlin/Heidelberg, Germany, 2012; pp. 305–322. [Google Scholar] [CrossRef]
- Leemans, S.J.J.; Fahland, D.; van der Aalst, W.M.P. Scalable Process Discovery and Conformance Checking. Softw. Syst. Model. 2018, 17, 599–631. [Google Scholar] [CrossRef] [Green Version]
- Weijters, A.; van der Aalst, W.M.P.; de Medeiros, A.A. Process Mining with the Heuristic Miner Algorithm, WP166; Eindhoven University of Technology: Eindhoven, The Netherlands, 2006. [Google Scholar]
- Grando, M.A.; Schonenberg, M.H.; van der Aalst, W.M.P. Semantic Process Mining for the Verification of Medical Recommendations. In HEALTHINF 2011—Proceedings of the International Conference on Health Informatics, Rome, Italy, 26–29 January 2011; Traver, V., Fred, A.L.N., Filipe, J., Gamboa, H., Eds.; SciTePress: Setúbal, Portugal, 2011; pp. 5–16. [Google Scholar]
- Pedrinaci, C.; Domingue, J.; Brelage, C.; van Lessen, T.; Karastoyanova, D.; Leymann, F. Semantic Business Process Management: Scaling Up the Management of Business Processes. In Proceedings of the 2nd IEEE International Conference on Semantic Computing (ICSC 2008), Santa Clara, CA, USA, 4–7 August 2008; IEEE Computer Society: Washington, DC, USA, 2008; pp. 546–553. [Google Scholar] [CrossRef] [Green Version]
- Smirnov, S.; Reijers, H.A.; Weske, M. From fine-grained to abstract process models: A semantic approach. Inf. Syst. 2012, 37, 784–797. [Google Scholar] [CrossRef]
- Bose, R.P.J.C.; van der Aalst, W.M.P. Abstractions in Process Mining: A Taxonomy of Patterns. In Proceedings of the Business Process Management, 7th International Conference, BPM 2009, Ulm, Germany, 8–10 September 2009; Lecture Notes in Computer Science. Dayal, U., Eder, J., Koehler, J., Reijers, H.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 159–175. [Google Scholar] [CrossRef]
- Haigh, K.Z.; Yaman, F. RECYCLE: Learning looping workflows from annotated traces. ACM TIST 2011, 2, 42. [Google Scholar] [CrossRef]
- Mendling, J.; Verbeek, H.M.W.; Dongen, B.F.; van der Aalst, W.M.P.; Neumann, G. Detection and prediction of errors in EPCs of the SAP reference model. Data Knowl. Eng. 2008, 64, 312–329. [Google Scholar] [CrossRef]
- Sadiq, S.; Marjanovic, O.; Orlowska, M. Managing change and time in dynamic workflow processes. Int. J. Coop. Inf. Syst. IJCIS 2000, 9, 93–116. [Google Scholar] [CrossRef] [Green Version]
- Vanhatalo, J.; Völzer, H.; Koehler, J. The Refined Process Structure Tree. In Business Process Management; Dumas, M., Reichert, M., Shan, M.-C., Eds.; Springer: Berlin/Heidelberg, Germany, 2008; pp. 100–115. [Google Scholar] [CrossRef]
- Polyvyanyy, A.; Smirnov, S.; Weske, M. The Triconnected Abstraction of Process Models. In Proceedings of the Business Process Management, 7th International Conference, BPM 2009, Ulm, Germany, 8–10 September 2009; Lecture Notes in Computer, Science. Dayal, U., Eder, J., Koehler, J., Reijers, H.A., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 229–244. [Google Scholar] [CrossRef] [Green Version]
- Baier, T.; Rogge-Solti, A.; Mendling, J.; Weske, M. Matching of Events and Activities: An Approach Based on Behavioral Constraint Satisfaction. In Proceedings of the 30th Annual ACM Symposium on Applied Computing, SAC ’15, Salamanca, Spain, 13–17 April 2015; Association for Computing Machinery: New York, NY, USA, 2015; pp. 1225–1230. [Google Scholar] [CrossRef] [Green Version]
- Fazzinga, B.; Flesca, S.; Furfaro, F.; Masciari, E.; Pontieri, L. A Probabilistic Unified Framework for Event Abstraction and Process Detection from Log Data. In Proceedings of the on the Move to Meaningful Internet Systems: OTM 2015 Conferences—Confederated International Conferences: CoopIS, ODBASE, and C&TC 2015, Rhodes, Greece, 26–30 October 2015; pp. 320–328. [Google Scholar] [CrossRef]
- Ferreira, D.R.; Szimanski, F.; Ralha, C.G. Improving process models by mining mappings of low-level events to high-level activities. J. Intell. Inf. Syst. 2014, 43, 379–407. [Google Scholar] [CrossRef]
- Leemans, S.J.J.; Goel, K.; van Zelst, S.J. Using Multi-Level Information in Hierarchical Process Mining: Balancing Behavioural Quality and Model Complexity. In Proceedings of the 2nd International Conference on Process Mining, ICPM 2020, Padua, Italy, 4–9 October 2020; Dongen, B.F., van Montali, M., Wynn, M.T., Eds.; IEEE: Piscataway, NJ, USA; pp. 137–144. [Google Scholar] [CrossRef]
- Leonardi, G.; Striani, M.; Quaglini, S.; Cavallini, A.; Montani, S. Leveraging semantic labels for multi-level abstraction in medical process mining and trace comparison. J. Biomed. Inform. 2018, 83, 10–24. [Google Scholar] [CrossRef] [PubMed]
- De Leoni, M.; Dundar, S. From Low-Level Events to Activities—A Session-Based Approach (Extended Version). arXiv 2019, arXiv:1903.03993. [Google Scholar]
- Tax, N.; Sidorova, N.; Haakma, R.; van der Aalst, W.M.P. Event Abstraction for Process Mining using Supervised Learning Techniques. arXiv 2016, arXiv:1606.07283. [Google Scholar]
- Van Zelst, S.J.; Mannhardt, F.; de Leoni, M.; Koschmider, A. Event abstraction in process mining: Literature review and taxonomy. Granul. Comput. 2020, 6, 719–736. [Google Scholar] [CrossRef]
- Gaily, F.; Alkhaldi, N.; Casteleyn, S.; Verbeke, W. Recommendation-Based Conceptual Modeling and Ontology Evolution Framework (CMOE+). Bus. Inf. Syst. Eng. 2017, 59, 235–250. [Google Scholar] [CrossRef]
- Guizzardi, G.; Figueiredo, G.; Hedblom, M.; Poels, G. Ontology-Based Model Abstraction. In Proceedings of the 13th International Conference on Research Challenges in Information Science (RCIS), Brussels, Belgium, 29–31 May 2019; pp. 1–13. [Google Scholar] [CrossRef] [Green Version]
- Dixit, P.M.; Verbeek, H.M.W.; Buijs, J.C.A.M.; van der Aalst, W.M.P. Interactive Data-Driven Process Model Construction. In Proceedings of the Conceptual Modeling—37th International Conference, ER 2018, Xi’an, China, 22–25 October 2018; Lecture Notes in Computer Science. Trujillo, J., Davis, K.C., Du, X., Li, Z., Ling, T.W., Li, G., Lee, M.-L., Eds.; Springer: Berlin/Heidelberg, Germany, 2018; pp. 251–265. [Google Scholar] [CrossRef]
- Greco, G.; Guzzo, A.; Lupia, F.; Pontieri, L. Process Discovery under Precedence Constraints. ACM Trans. Knowl. Discov. Data 2015, 9, 32. [Google Scholar] [CrossRef]
- Rembert, A.J.; Omokpo, A.; Mazzoleni, P.; Goodwin, R. Process Discovery Using Prior Knowledge. In Proceedings of the Service-Oriented Computing 11th International Conference, ICSOC 2013, Berlin, Germany, 2–5 December 2013; Lecture Notes in Computer, Science. Basu, S., Pautasso, C., Zhang, L., Fu, X., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 328–342. [Google Scholar] [CrossRef]
- Maggi, F.M.; Bose, R.P.J.C.; van der Aalst, W.M.P. A Knowledge-Based Integrated Approach for Dis-covering and Repairing Declare Maps. In Proceedings of the Advanced Information Systems Engineering—25th International Conference, CAiSE 2013, Valencia, Spain, 17–21 June 2013; Lecture Notes in Computer Science. Salinesi, C., Norrie, M.C., Pastor, O., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 433–448. [Google Scholar] [CrossRef]
- Schuster, D.; van Zelst, S.J.; van der Aalst, W.M.P. Cortado—An Interactive Tool for Data-Driven Process Discovery and Modeling. In Proceedings of the Application and Theory of Petri Nets and Concurrency—42nd International Conference, PETRI NETS 2021, Virtual Event, 23–25 June 2021; Lecture Notes in Computer, Science. Buchs, D., Carmona, J., Eds.; Springer: Berlin/Heidelberg, Germany, 2021; pp. 465–475. [Google Scholar] [CrossRef]
- Benevento, E.; Dixit, P.M.; Sani, M.F.; Aloini, D.; van der Aalst, W.M.P. Evaluating the Effectiveness of Interactive Process Discovery in Healthcare: A Case Study. In Business Process Management Workshops—BPM 2019 International Workshops, Vienna, Austria, 1–6 September 2019; Revised Selected Papers, Lecture Notes in Business Information Processing; Di Francescomarino, C., Dijkman, R.M., Zdun, U., Eds.; Springer: Berlin/Heidelberg, Germany; pp. 508–519. [CrossRef]
- Valero-Ramon, Z.; Fernández-Llatas, C.; Valdivieso, B.; Traver, V. Dynamic Models Supporting Personalised Chronic Disease Management through Healthcare Sensors with Interactive Process Mining. Sensors 2020, 20, 5330. [Google Scholar] [CrossRef] [PubMed]
- Mans, R.; van der Aalst, W.M.P.; Vanwersch, R.; Moleman, A. Process Mining in Healthcare: Data Challenges When Answering Frequently Posed Questions. In ProHealth/KR4HC; Lecture Notes in Computer Science; Lenz, R., Miksch, S., Peleg, M., Reichert, M., Riaño, D., ten Teije, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; pp. 140–153. [Google Scholar] [CrossRef]
- Mans, R.; Schonenberg, H.; Leonardi, G.; Panzarasa, S.; Cavallini, A.; Quaglini, S.; van der Aalst, W.M.P. Process Mining Techniques: An Application to Stroke Care. In Proceedings of MIE, Studies in Health Technology and Informatics; Andersen, S., Klein, G.O., Schulz, S., Aarts, J., Eds.; IOS Press: Amsterdam, The Netherlands, 2008; pp. 573–578. [Google Scholar] [CrossRef]
- Mans, R.; Schonenberg, H.; Song, M.; van der Aalst, W.M.P.; Bakker, P. Application of process mining in healthcare—A case study in a Dutch hospital. In Biomedical Engineering Systems and Technologies, Communications in Computer and Information Science; Fred, A., Filipe, J., Gamboa, H., Eds.; Springer: Berlin/Heidelberg, Germany, 2009; pp. 425–438. [Google Scholar] [CrossRef]
- Perimal-Lewis, L.; Qin, S.; Thompson, C.; Hakendorf, P. Gaining Insight from Patient Journey Data using a Process-Oriented Analysis Approach. In Proceedings Workshop on Health Informatics and Knowledge Management (HIKM); Conferences in Research and Practice in Information Technology; Butler-Henderson, K., Gray, K., Eds.; Australian Computer Society: Sydney, Australia, 2012; pp. 59–66. [Google Scholar]
- Rojas, E.; Munoz-Gama, J.; Sepulveda, M.; Capurro, D. Process mining in healthcare: A literature review. J. Biomed. Inform. 2016, 61, 224–236. [Google Scholar] [CrossRef]
- International Health Terminology Standards Development Organisation. SNOMED Clinical Terms. 2015. Available online: http://www.ihtsdo.org/snomed-ct (accessed on 24 October 2022).
- Nahler, G. Anatomical therapeutic chemical classification system (ATC). In Dictionary of Pharmaceutical Medicine; Springer: Vienna, Austria, 2009; p. 8. [Google Scholar] [CrossRef]
- McGuinness, D.L.; van Harmelen, F. OWL Web Ontology Language. 2004. Available online: http://www.w3.org/TR/owl-features/ (accessed on 24 October 2022).
- Thompson, K. Programming Techniques: Regular Expression Search Algorithm. Commun. ACM 1968, 11, 419–422. [Google Scholar] [CrossRef]
















Publisher’s Note: MDPI stays neutral with regard to jurisdictional claims in published maps and institutional affiliations. |
© 2022 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (https://creativecommons.org/licenses/by/4.0/).
Share and Cite
Bottrighi, A.; Guazzone, M.; Leonardi, G.; Montani, S.; Striani, M.; Terenziani, P. Integrating ISA and Part-of Domain Knowledge into Process Model Discovery. Future Internet 2022, 14, 357. https://doi.org/10.3390/fi14120357
Bottrighi A, Guazzone M, Leonardi G, Montani S, Striani M, Terenziani P. Integrating ISA and Part-of Domain Knowledge into Process Model Discovery. Future Internet. 2022; 14(12):357. https://doi.org/10.3390/fi14120357
Chicago/Turabian StyleBottrighi, Alessio, Marco Guazzone, Giorgio Leonardi, Stefania Montani, Manuel Striani, and Paolo Terenziani. 2022. "Integrating ISA and Part-of Domain Knowledge into Process Model Discovery" Future Internet 14, no. 12: 357. https://doi.org/10.3390/fi14120357
APA StyleBottrighi, A., Guazzone, M., Leonardi, G., Montani, S., Striani, M., & Terenziani, P. (2022). Integrating ISA and Part-of Domain Knowledge into Process Model Discovery. Future Internet, 14(12), 357. https://doi.org/10.3390/fi14120357