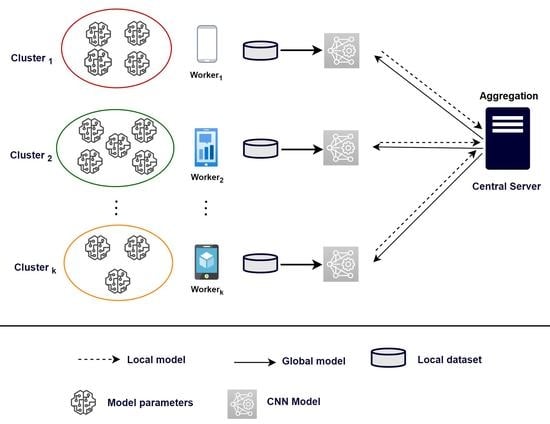
In this section, we first study the clustering optimization scheme used for the dynamic adaptation of partitioning of workers’ updates at each communication round. This adaptive behavior contributes to achieving robust communication in FL. The performance of the proposed FedCO is then evaluated and compared to three other existing FL approaches (FedAvg, FedProx, and CMFL) in terms of accuracy, communication rounds, and communication overhead.
Our proposed FedCO algorithm is a communication-optimized version of FedAvg. Therefore, we further evaluate these two algorithms by benchmarking them on two datasets from the LEAF Federated Learning repository, namely FEMNIST and CelebA. In addition, we further study our FedCO algorithm for two different scenarios for selecting cluster representatives: a performance threshold-based worker selection versus the single (top-performer) cluster representative selection, explained in Algorithm 1.
6.1. Clustering Optimization Behavior
Our clustering optimization algorithm assesses the local updates of clusters’ representatives at each communication round, and as a result, it assigns some workers to different clusters. An output of this cluster-updating procedure is that clusters may appear or disappear. Our solution is capable of catching and handling these scenarios. In addition, it implements a splitting procedure that performs a further fine calibration of the clustering for the newly uploaded updates.
In order to illustrate the properties of the clustering optimization scheme discussed above, we show in
Figure 4 the clustering updates in the first five global communication rounds of the FedCO algorithm applied to the Non-IID FashionMNIST dataset. In the example, in round 2, cluster 5 has disappeared and cluster 3 is a singleton, i.e., it cannot be a candidate for splitting. Almost all of the remaining clusters (except cluster 6) have negative SI scores. The remaining clusters (0, 1, 2, 4, and 7) have been split into two new clusters and their cluster labels are replaced. Interestingly, in round 3, the unique number of clusters is 17. However, in round 4, five clusters have turned out empty and have disappeared (1, 4, 10, 13, and 16). Furthermore, eight clusters have positive SI scores (0, 2, 5, 6, 9, 12, 14, and 15), while four have negative SI scores (3, 7, 8, and 11). The algorithm did not split the clusters 7, 8, and 11 because this did not improve the quality of the clustering solution; i.e., it did not increase its SI score. Cluster 3 is still a singleton. The worker belonging to this cluster may be considered as one that provides unique model parameters due to its training data. Consequently, in round 5, we have only 12 clusters. Two clusters disappeared (2 and 14), and four new clusters appeared (1, 6, 12, and 17), while clusters 3 and 9 were singletons.
The cluster optimizations discussed above will continue in the same fashion for the upcoming communication rounds. The workers’ partitioning is dynamically adapted at each communication round to reflect the new local updates of the representatives.
6.2. Convergence Analysis
In this section, we provide a convergence analysis of the proposed FedCO algorithm and theoretically show that it ensures a faster convergence than the baseline FedAvg algorithm.
Our analysis is based on two assumptions. The first one supposes that the data are non-IID. Secondly, we assume that there is a partial involvement of workers; this strategy is much more realistic as it does not require all of the worker output. Therefore, at each iteration, we can calculate the global update by aggregating the local updates by using those cluster representatives, which have reached a high accuracy level at this iteration phase. Two scenarios are considered to this end: (i) a global model is trained by FedAvg based on updates made by randomly selected workers, regardless of their accuracy value; (ii) a global model is trained by applying FedCO, and in that way, at each training round, only workers (cluster representatives) that have achieved the highest accuracy values are used.
Let us briefly summarize the working mechanism of the proposed FedCO algorithm. In the
tth global training iteration, each worker involved (
) calculates the average
gradients using the optimization algorithms in the local dataset in the current global model
. Note that according to Equation (
5), high-quality data and a high accuracy of the workers’ models can lead to a faster convergence of the local loss functions (Equation (
3)) and the global loss function (Equation (
4)) [
45]. Both the local model update
of the worker in Equation (
1) and the shared global model update
in Equation (
5) can be more quick to converge to the target value with fewer iterations. Consequently, the training time of a worker in a global iteration is decreasing. Therefore, highly accurate workers’ models can significantly improve the learning efficiency of Federated Learning; e.g., it can ensure less training time [
31,
46]. This process is iterative until a global accuracy
(
) is achieved. Specifically, each update of the local model has a local accuracy
that corresponds to the local quality of the worker
data. A higher local accuracy leads to fewer local and global iterations [
46,
47]. FedCO uses an iterative approach that requires a series of communication rounds to achieve a level of global accuracy
. Server and representative communications occur during each global round of the iteration phase. Specifically, each representative minimizes its objective
in Equation (
3) using the local training data
. Minimizing
in Equation (
4) also requires multiple local iterations up to a target accuracy. Then, the global rounds will be bounded as follows:
Thus, the global rounds are affected by both the global accuracy
and the local accuracy
. When
and
are high, FedCO needs to run a few global rounds. On the other hand, each global round consists of both computation and transmission time. Our primary motivation in this work is to consider the communication overhead, discussed and analyzed in detail in
Section 6.3. The computation time (
), however, depends on the number of local iterations. When the global accuracy
is fixed, the computation time is bound by
for an iterative algorithm to solve Equation
1; here, (SGD) is used [
46]. Therefore, the total time of one global communication round for a set of representatives is denoted as
where
represents the transmission time of a local model update. As a result, a high local accuracy value of
leads to fewer local iterations
and eventually to lower global communication rounds
. Unlike FedCO’s convergence rate, FedAvg does not necessarily guarantee a faster convergence speed. This is because FedAvg uses a much larger number of workers compared to the FedCO model. Therefore, if there are more workers with poor data quality, the convergence will be reached at a slower rate than when much fewer workers with high data quality are used. However, at each global round, FedCO may have selected a different set of workers. Those, however, are not selected randomly, but each one is a representative of a cluster of workers having modeled similar parameters, and in addition, it achieves the highest accuracy among the cluster members. Let
and
represent the number of global rounds for which convergence has been reached by FedAvg and FedCO, respectively. Then,
Table 4 and
Table 5 demonstrate that the inequality
is valid in the experiments aiming to reach the same accuracy using the two algorithms.
6.3. Communication Rounds versus Accuracy
In this subsection, we present the results related to the evaluation of the accuracy of our distributed deep learning (DL) model.
Figure 5,
Figure 6 and
Figure 7 show how the compared FL (FedAvg, FedProx, CMFL, and FedCO) algorithms perform in terms of Accuracy versus the Number of Communication Rounds. For the MNIST dataset (see
Figure 5), we can observe that the FedCO algorithm converges faster than with the state-of-the-art approaches. As is shown in
Figure 5a (IID data distribution setting), FedAvg and FedProx use 100 rounds to obtain an accuracy of
. The CMFL reaches the same accuracy in 30 rounds, while our FedCO algorithm achieves this result with only 10 rounds. Furthermore, in
Figure 5b, FedCO dramatically decreases the communication rounds with respect to FedAvg, FedProx, and CMFL. Indeed, in Non-IID data, a learning accuracy of
is achieved by FedCO in 40 rounds, FedAvg has conducted 160 rounds, FedProx requires 200 rounds, and CMFL needs 60.
In
Figure 6a, we compare the accuracy of the four FL approaches in the case of the IID data distribution scenario of FashionMNIST. The FedCO outperforms FedAvg, FedProx, and CMFL in this experimental setting. Within 25 communication rounds, CMFL, FedAvg, and FedProx reach
,
, and
accuracy, respectively, while our FedCO algorithm achieves an accuracy of
with the same number of communication rounds. Notice that under the Non-IID data distribution setting, our FedCO algorithm outperforms the other, reaching an accuracy of nearly
with only 11 rounds; this costs 100 communication rounds for FedAvg and 80 rounds for FedProx. CMFL considerably minimizes this cost to 60; see
Figure 6b.
Finally, for the CIFAR-10 IID data, the required communication costs of the FedAvg and FedProx to achieve
accuracy is 150 rounds, while CMFL obtains the same result for 75 rounds. Our FedCO algorithm outperforms the others, needing only nine rounds to reach this accuracy value (cf.
Figure 7a). In the case of the CIFAR-10 Non-IID data (see
Figure 7b), in 25 communication rounds, FedCO obtains an accuracy of
, while FedAvg and FedProx reach
and
, respectively. On the other hand, CMFL achieves a close result
of accuracy in the same number of rounds.
FedCO differs from the Federated Learning baseline FedAvg as follows: our algorithm uses a much smaller number of nodes while the aggregation procedure is the same. Thus, if we have a smaller number of workers, convergence is reached faster than in FedAvg, where all the available workers are used. At each round, FedCO selects and uses a different set of workers, and each worker is a representative that achieves the highest accuracy in each cluster. Hence, the accuracy is not sacrificed.
Table 4 shows the number of communication rounds to achieve the maximum model accuracy (i.e., to converge) for the datasets considered. Specifically, the target accuracy values are
for MNIST and FashionMNIST and
for CIFAR-10. FedAvg is the baseline benchmark, and the iterations saved for algorithm
X (
X = FedProx, CMFL, or FedCO) is computed as
FedCO saves from
to
of iterations to converge with respect to FedAvg for IID data distribution setting, and it saves from
to
iterations for the Non-IID data distribution scenario. Moreover, FedCO always converges with at least half of the iteration rounds needed by CMFL. In more detail, one can observe that the model on the MNIST IID data distribution setting converges to an accuracy of
in 190 rounds with the FedAvg algorithm, and in 25 rounds for our FedCO algorithm, providing savings of
, and in 185 rounds for FedProx, and in 50 rounds for CMFL, providing savings of
and
, respectively. The model trained on the FashionMNIST IID data distribution scenario converges to a target accuracy of
in 200 rounds for FedAvg, and in 50 rounds for FedCO, saving
of communication rounds, while it requires 190 and 60 rounds for FedProx (
saving) and CMFL (
saving), respectively. Furthermore, in the FashionMNIST Non-IID data distribution scenario, the model converges to an accuracy of
in 200 rounds for the FedAvg algorithm, and in 186 rounds for FedProx, saving only
. In contrast, it requires 70 and 150 communication rounds for FedCO and CMFL, with savings of
and
, respectively. The experimental results on the CIFAR-10 data show that the model trained in the IID and Non-IID data settings need 200 rounds for FedAvg to reach
of the accuracy, while it requires 188 rounds for FedProx to reach
in IID, and more than 200 rounds in Non-IID to obtain target accuracy. On the other hand, FedCO and CMFL require 30 and 80 rounds, respectively, to converge under the IID data distribution scenario. Furthermore, within the Non-IID data distribution setting, the model converges to an accuracy of
in 200 rounds for the FedAvg, while it requires 60 and 160 communication rounds for FedCO and CMFL, respectively. Similarly, in the Non-IID data distribution setting, the FedCO communication costs are reduced to
with the MNIST data,
with the FashionMNIST data, and up to
with the CIFAR-10 dataset, compared to the FedAvg.
Although FedProx is considered to be an optimized version of FedAvg, we can observe from the results discussed above that FedProx behaves very similarly to FedAvg and shows only a slightly better performance than FedAvg in the conducted experiments. In addition, as we mentioned earlier, our FedCO algorithm can also be interpreted as an optimized version of FedAvg. Therefore, we further study these two algorithms (FedCO and FedAvg) by conducting experiments and benchmarking their performance on two datasets from the LEAF repository, namely FEMNIST and CelebA.
Figure 8 shows the final accuracy scores after several rounds of communication for the FEMNIST dataset. Comparing the results produced by the two methods, it is evident that FedCO performs significantly better than FedAvg, on both the IID and Non-IID data scenarios. Specifically, FedCO ensures a higher accuracy than that of FedAvg within a smaller number of communication rounds. For example, in
Figure 8a, FedCO can reach
in only 110 iterations, while the FedAvg never reaches that level within 200 iterations.
Analyzing the results in
Figure 9, we can observe the following: (1) FedCO consistently outperforms FedAvg in both data distribution scenarios; (2) FedCO generally achieves better accuracies than FedAvg in most cases (see
Figure 9b), considering that both of them have been trained with only 200 rounds.
Table 5 reports the number of communication rounds that the FedAvg and FedCO algorithms need in order to converge, for the considered datasets. Specifically, the target accuracy values are
for FEMNIST and
for CelebA, respectively. In addition, FedAvg is considered as the baseline.
Note that these results again verify the faster convergence of FedCO compared to that of FedAvg. Notice that we have also studied and compared FedProx and FedAvg on the same LEAF datasets, and they again have demonstrated very similar behaviors.
6.4. Communication Overhead Analysis
In this section, we compare the efficiencies of the two compared FL algorithms for 100 communication rounds with respect to different numbers of workers on the CIFAR-10 and the MNIST datasets, under the IID and Non-IID data distribution scenarios. The obtained results are reported in
Figure 10 and
Figure 11, respectively. As one can notice, the FedCO algorithm has performed significantly better than the FedAvg, FedProx, and CMFL. The reader can also observe that the communication overhead increases linearly with the number of workers. Hence, to scale in a real scenario with thousands of workers, a FL algorithm should be capable of reducing the communication cost as much as possible, and reducing the number of rounds to converge, as with the proposed FedCO algorithm. Finally, the communication overhead in the IID and Non-IID cases is very close or identical. The results produced on the FashionMNIST dataset are similar to the other two datasets.
The communication cost savings for algorithm
X (
X = FedProx, CMFL, or FedCO) is computed as
As can be seen in
Figure 10a,b, the FedCO costs on the CIFAR-10 IID data are 1 MB for 20 workers, which is a reduction in communication costs by
in comparison with FedAvg, while FedProx and CMFL are allowed to save only
and
in communication costs, respectively. In an experiment involving 100 workers on the CIFAR-10 dataset, FedAvg, FedProx, and CMFL exchange 32.5, 31.04, and 20 MB of data, while the proposed FedCO consumes only 5.4 MB, which means that FedCO reduces the communication overhead by
with respect to FedAvg, and CMFL reduces the communication overhead by
, while FedProx saves only
in communication costs.
Figure 11a,b report the communication costs under the MINIST IID and Non-IID data distribution scenarios, respectively. The trend is similar to the results of the CIFAR-10 data experiments. Both the IID and Non-IID data distribution settings confirm that our FedCO algorithm ensures a significantly smaller communication overhead in comparison with FedAvg, FedProx, and CMFL, by substantially reducing the required number of bytes exchanged. As can be noticed, FedCO allows a saving of between
and
with respect to FedAvg. In
Figure 10 and
Figure 11, the communication costs increase linearly with the increasing number of workers for all of the compared algorithms. It is obvious that FedCO consistently outperforms FedAvg, FedProx, and CMFL in terms of reducing communication costs.
6.5. Threshold-Based Worker Selection
We also study scenarios in which we use an accuracy threshold to select the number of workers. The threshold is the specified cut-off of accuracy value for the selection of representatives of a cluster of workers. We select any worker where the local update ensures an accuracy of greater than or equal to the predefined threshold as a representative of a cluster. In this section, we report the results produced by testing four different threshold values for FedCO, namely
,
,
, and
. The network threshold for the selection of workers varies from bandwidth, transmission speed, or packet loss [
48].
Table 6 reports the number of the top-ranked workers that the FedCO algorithm has selected to communicate with the server when the predefined threshold is met within 100 communication rounds.
In the case of the CelebA data, the highest number of representatives has been selected when the accuracy of the local models is equal to or above
, namely 853 and 826 workers under IID and Non-IID, respectively. In the experiments conducted on the FEMNIST data, when the threshold of the local models was greater than or equal to
, 912 workers were selected as representatives for the IID scenario, and 844 workers for the Non-IID one. Similarly, these two values represent the highest numbers of selected workers. It is obvious from the number of representatives reported in
Table 6 that the low threshold value implies the greater number of representatives to be selected for global training in FL and vice versa. Thus, we can observe that the proposed algorithm substantially reduces the accumulated communication overhead when FedCO selects only
k representatives (i.e., one per cluster), rather than selecting a variable number of representatives based on a predefined threshold to train a global model.
Table 7 presents how many workers per round have been selected as representatives when various thresholds are applied for CelebA under the IID and Non-IID data scenarios, respectively.
We can see that until 10 communication rounds, the FedCO selects only k representatives, since there are no local models where the accuracy has reached at 10 rounds. Thus, the number of representatives increases from 10 to 97 at round 12 due to the selection of all the clusters’ workers, ensuring an accuracy that is equal to or above the given threshold. Notice that there are 97 workers of different clusters that reach the value of accuracy of their local models of or above. We can see that FedCO needs 30 rounds to have a number of workers whose accuracy is greater than or equal to and to meet this condition under IID data. Furthermore, to meet the threshold of , FedCO requires 100 rounds to have a number of workers (98) such that their accuracy of the local models meets this condition under IID. On the other hand, for Non-IID, FedCO never meets this condition, since no local models have a accuracy value of higher than or equal to ; thus, FedCO selects only 36 workers to represent the different clusters.
Figure 12 provides communication overheads for various thresholds. It is obvious to the reader that a higher number of selected representatives implies a higher values of communication costs to the server.
The above results suggest that our proposed FedCO algorithm can substantially reduce the communication overhead by using a higher accuracy threshold. In general, FedCO can be considered as being robust to different application scenarios by being able to tune its parameters (e.g., the accuracy threshold or the number of top-ranked representatives per cluster) to find a trade-off between the application-specific resource constraints and the accuracy requirements.