Design of Unsignalized Roundabouts Driving Policy of Autonomous Vehicles Using Deep Reinforcement Learning

Abstract

Driving at an unsignalized roundabout is a complex traffic scenario that requires both traffic safety and efficiency. At the unsignalized roundabout, the driving policy does not simply maintain a safe distance for all vehicles. Instead, it pays more attention to vehicles that potentially have conflicts with the ego-vehicle, while guessing the intentions of other obstacle vehicles. In this paper, a driving policy based on the Soft actor-critic (SAC) algorithm combined with interval prediction and self-attention mechanism is proposed to achieve safe driving of ego-vehicle at unsignalized roundabouts. The objective of this work is to simulate a roundabout scenario and train the proposed algorithm in a low-dimensional environment, and then test and validate the policy in the CARLA simulator to ensure safety while reducing costs. By using a self-attention network and interval prediction algorithms to enable ego-vehicle to focus on more temporal and spatial features, the risk of driving into and out of the roundabout is predicted, and safe and effective driving decisions are made. Simulation results show that our proposed driving policy can provide collision risk avoidance and improve vehicle driving safety, resulting in a 15% reduction in collisions. Finally, the trained model is transferred to the complete vehicle system of CARLA to validate the possibility of real-world deployment of the policy model.

1. Introduction

The unsignalized roundabout is one of the most challenging traffic scenarios in urban environments [1]. Individual drivers should decide whether to cross over (or turn to) their route without signalized protection at the roundabout. Therefore, it makes sense for autonomous vehicles to learn how to get through this scenario. In such a complex scenario, the ego-vehicle must consider the direction of surrounding obstacle vehicles and judging obstacle vehicle intentions. The existing approaches to this problem fall into three main categories: rule-based, collaborative scheduling-based, and learning-based. Traditional rule-based decision policies have the disadvantage of small decision space and long computation time and cannot be applied to complex scenarios [2]. Because rule-based decision policies are usually constructed from human knowledge and engineering experience, most use Time-To-Collision (TTC) as a safety indicator to ensure a safe distance between two vehicles [3]. Although this method can satisfy most driving conditions, the designed rules lack flexibility and adaptability in complex environments such as non-fiduciary controlled intersections. If new rules are written for each special working condition, the independence and compatibility between functions also need to be fully considered, so it is unrealistic to take into account all special working conditions. The collaborative scheduling-based approach uses road measurement equipment to obtain vehicle-to-vehicle information and perform overall scheduling of vehicles at intersections to complete the passage of vehicles at non-information-controlled intersections [4]. However, this approach has limitations and low scalability in reality as it requires the installation of expensive infrastructure. Learning-based approaches obtain optimal policies by neural networks learning from expert driving databases [5] or empirical data [6] in a training environment. The trained policies are real-time, do not require complex rules to be constructed by humans, and have great advantages and potential for handling autonomous driving decision problems. However, the driving dataset needs to contain a wider and broader range of scenarios, so it is difficult to obtain a good-quality dataset.

Therefore, deep learning or deep reinforcement learning methods have attracted the attention of scholars. Deep reinforcement learning is used to allow an agent to learn on its own by a simulated scenario through simulation, without the need to create a dataset, just by providing a training simulation. So, deep reinforcement learning (DRL) [7], with its unique ability to interact with the environment and self-learning capability, has been widely used in autonomous driving policy.

1.1. Literature Review

DRL is one of the common approaches to solving autonomous driving behavior decision problems in recent years [8]. In simple scenarios, simple autonomous driving tasks such as lane-keeping, lane-changing, and adaptive cruise (ACC) are solved based on deep reinforcement learning. Song et al. [9] investigated a combination of imitation-learning and reinforcement-learning policy for vehicle lane-changing decisions, which has a faster policy learning speed than simple reinforcement learning methods. Guo et al. [10] proposed a driver following a deterministic policy gradient (DDPG) algorithm that has comparable to real human drivers’ following behavior. However, the simple scenarios above are all about controlling the longitudinal movement of the vehicle and do not deal with the lateral movement of the vehicle, for example in terms of lane changing.

In complex scenarios, deep reinforcement learning has been used to implement merging on high-speed ramps [11], passing intersections [12], and passing modern roundabouts [13,14,15]. However, challenges remain for behavioral decision-making in the such complex road, multi-vehicle interaction, and traffic rule-constrained scenarios. Some algorithms have been proposed to improve the success rate and safety of behavioral decision-making. Edouard Leurent et al. [16,17] utilized interval prediction and search-trees for behavioral decision-making to improve the success rate through intersections, due to the use of decision search-trees. If the complexity of the environment, namely the branches of the search-trees, will grow geometrically, the search time will gradually increase, and cannot guarantee the real-time decision-making policy. Joseph Lubars et al. [18] and Williams et al. [19] applied a combination of reinforcement learning and Model Predictive Control (MPC) to solve autonomous driving in ramp merging scenarios. They adopted MPC to constrain ego-vehicle control commands for collision avoidance purposes but did not study complex roundabouts or intersections. Furthermore, MPC increases the computing power requirement with the complexity of the environment. Meanwhile, the neural networks’ policy model cannot explain the driving process well. Some scholars used self-attention networks to calculate the attention weights to surrounding vehicles, Wang J et al. [20] studied Self-Attention Network [21] to extract the environmental vehicle information and calculate the attention weights of different vehicles to visualize the explanation of decision-making interactions of ego-vehicles with other vehicles, but which is too aggressive or dangerous occasionally. Therefore, getting a safer, rational, and interpretable autonomous driving policy is a key technical challenge urgently needed for current autonomous vehicles.

1.2. Contribution

Aiming at the complex unsignalized roundabout, this paper proposed an autonomous driving policy: Interval Prediction with Soft Actor-Critical (IP-SAC). IP-SAC combines deep reinforcement learning with interval prediction models and self-attention networks to improve ego-vehicle driving safety. In the simulation environment, ego-vehicle has increased success rates and reduced risk factors for entrances and exits. To further test the policy, the trained model was validated in a CARLA simulator. The results show that the ego-vehicle can safely drive in the CARLA roundabout.

The remainder of the paper is organized as follows. The simulation roundabout scenario is described in Section 2. The IP-SAC is described in detail in Section 3. Simulations are designed to evaluate the performance of the IP-SAC algorithm and analysis simulation results, and the IP-SAC policy is validated in a CARLA roundabout in Section 4. The final section is the conclusion of the paper.

2. Roundabout Scenario

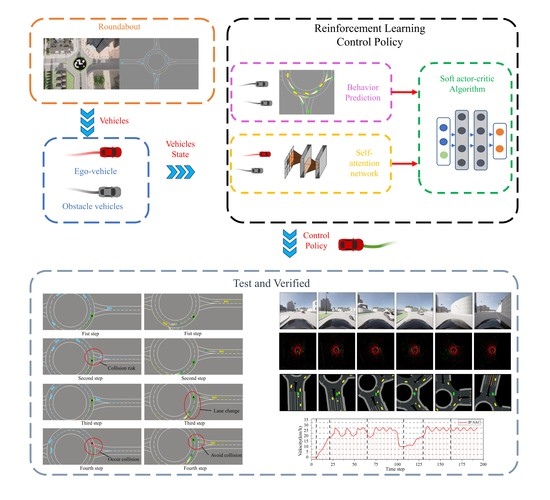
Scenario building is critical for training and evaluating the performance of autonomous vehicle driving policy. The generic approach is to test the safety of the driving policy in a natural environment but, considering the high dimensional characteristics of the environment and the probability of conflicting collision events, thousands of kilometers or multiple time cycles will be required to verify the safety of the policy, and this testing approach is very costly. In this paper, the policy algorithm is trained and improved in a simple low-dimensional simulation scenario and verified in a high-dimensional environment. The low-dimensional simulation environment has a low dimensionality and a higher incidence of conflicting collision events compared with the high-dimensional environment. Moreover, the simulation environment is parallel, and multiple environments can be tested simultaneously to accelerate the training and evaluation process.

2.1. Roundabout Simulation Scenario Construction

The research scenario is an unsignalized roundabout. Most of the autonomous driving algorithms are tested by building simulation scenarios based on natural environments, such as CARLA, Microsoft Air-Sim, NVIDIA Driver Constellation, Google/Waymo Car-Craft, and Baidu AADS. However, all these scenarios suffer from inefficiency and the driving policies are vulnerable to the influence of perception algorithms. The driving policies cannot focus on vehicle decisions, resulting in long training time or failure to converge. Therefore, it is necessary to use a low-dimensional simulation environment to verify the reinforcement learning decision algorithm, which is not affected by the perception algorithms and focuses more on the improvement of the algorithm itself. We compare six mainstream reinforcement learning simulation platforms: TORCS, Highway-ENV, CARLA, SMARTS, Driver-Gym, and SUMO, as shown in

Table 1. Comparison of reinforcement learning simulation platforms.

Platform	Low Dimensionality	Simulation Accuracy	Easy Development
TORCS	×	√	×
CARLA	×	√	√
SMARTS	√	√	×
SUMO	√	×	√
Driver-Gym	×	√	×
Highway-ENV	√	√	√

. After considering low-dimensionality, simulation accuracy, and development time, based on Python/Gym, we choose the Highway-Env [22] as the low-dimensional simulation platform and CARLA as the high-dimensional simulation platform.

To specifically study the roundabout scenario problem, by referring to the Chinese miniature unsignalized roundabout standards and base the CARLA Town3 map, we simplified and built a 25-m radius roundabout scenario, each vehicle’s dimensions are set at 5 m in length and 1.6 m in width, and roundabout road width of 3.75 m. In the roundabout, the ego-vehicle (autonomous vehicle) makes behavioral actions and interacts with obstacle vehicles. The ego-vehicle, from the starting point to the destination, is shown in Figure 1.

2.2. Roundabout Obstacle Vehicles Control

In the Highway-Env, the Kinematic Bicycle model is used to simulate the motion of the vehicles, which are controlled using a hierarchical architecture: top-level control and bottom-level control. The bottom control is divided into longitudinal control and lateral control. The longitudinal control uses a simple proportional controller to control vehicle acceleration, as Equation (1).

$$a=K_p\left(v_r-v\right)$$

(1)

where $a$ is the vehicle acceleration, $K_p$ is the controller proportional gain, $v_r$ is the vehicle reference speed, $v$ is the vehicle current speed.

The lateral control is divided into position control and heading control, which combines the vehicle kinematic model to calculate the front wheel angle of the vehicle through a proportional differential controller.

Lateral position controls are given by Equations (2) and (3):

$$v_{lat,r}=-K_{p,lat}{\Delta }_{lat}$$

(2)

$$\Delta {\psi }_r=\mathit{arcsin}\frac{v_{lat,r}}{v}$$

(3)

Heading control is given by Equations (4)–(6):

$${\psi }_r={\psi }_L+\Delta {\psi }_r$$

(4)

$${\dot{\psi }}_r=K_{p,\psi }\left({\psi }_r-\psi \right)$$

(5)

$$\delta =\mathit{arcsin}\left(\frac{1}{2}\frac{1}{v}{\dot{\psi }}_r\right)$$

(6)

where $v_{lat,r}$ is the lateral velocity, $K_{p,lat}$ is the lateral position control gain, ${\Delta }_{lat}$ is the lateral offset of the vehicle relative to the lane centerline, $\Delta {\psi }_r$ is the heading angle to compensate for the lateral position, $v$ is the current vehicle speed, ${\psi }_r$ is the vehicle target heading, ${\psi }_L$ is the heading required for the look-ahead distance (to predict the turn), ${\dot{\psi }}_r$ is the vehicle heading transverse swing rate, $K_{p,\psi }$ is the heading control gain, $\psi$ is the current vehicle heading, and $\delta$ is the front wheel angle.

Top-level control determines vehicle behaviors, such as controlling vehicle acceleration, lane keeping, and lane changing. The behavior is divided into longitudinal behavior and lateral behavior according to the behavior.

The longitudinal behavior controls the acceleration of the vehicle with the Intelligent Driver Model (IDM) control model as Equations (7) and (8). The IDM parameters are shown in

Table 2. IDM parameters.

Parameters	Value
Maximum acceleration $\omega$	6.0 m/s2
Constant velocity parameter $\delta$	4.0
Safety time interval $T$	1.5 s
Maximum deceleration $b$	−5.0 m/s2
Minimum relative distance $d_0$	10.0 m

.

$$a=\omega \left[1-{\left(\frac{v}{v_0}\right)}^{\delta }-{\left(\frac{d^{*}}{d}\right)}^2\right]$$

(7)

$$d^{*}=d_0+Tv+\frac{v\Delta v}{2\sqrt{ab}}$$

(8)

where $a$ is the vehicle acceleration, $\omega$ is the maximum vehicle acceleration, $v$ is the current vehicle speed, $v_0$ is the target speed, $\delta$ is the constant velocity parameter, $d$ is the distance from the front vehicle, $d^{*}$ is the desired spacing, $d_0$ is the minimum relative distance between vehicles, $T$ is the safety time interval, $b$ is the maximum deceleration of the vehicle.

The lateral behavior is determined by the MOBIL model based on the acceleration of surrounding vehicles to decide when to change lanes when the following conditions are met, as Equations (9) and (10):

$${\tilde{a}}_n\ge -b_{safe}$$

(9)

$$\underset{ego-vehicle}{\underbrace{{\tilde{a}}_c-a_c}}+p\left(\underset{new follower}{\underbrace{{\tilde{a}}_n-a_n}}+\underset{old follower}{\underbrace{{\tilde{a}}_o-a_o}}\right)\ge \Delta a_{th}$$

(10)

where c is controlled(ego-) vehicle, n is the old follower before controlled vehicle lane change, o is the new follower after controlled vehicle lane change lane change, $b_{\mathrm{safe}}$ is the maximum braking deceleration of the controlled vehicle, $a$, $\tilde{a}$ is the acceleration of the controlled vehicle before and after the lane change, respectively, $p$ is the conservative factor, and $\Delta a_{\mathrm{th}}$ is the acceleration threshold that triggers whether to change lanes.

To test the effectiveness and reliability of the driving policy, IDM and MOBIL control the obstacle vehicles added in the unsignalized roundabout. The obstacle vehicles are considered being driven by a human driver and appear randomly in the roundabout scenario. Each obstacle vehicle has its own route and destination for simulating vehicles encountered in reality. In a real-life scenario, the obstacle vehicle can be either a vehicle with autonomous driving capabilities or an ordinary vehicle driven by a human. The ego-vehicle senses the surrounding obstacle vehicles through machine vision, LIDAR, and other sensing sensors combined with sensing algorithms, and passes the sensing results (in this paper, the information on the location of the obstacle vehicle is used as a sensing result) to the decision-making policy.

2.3. Ego-Vehicle Control

The ego-vehicle can observe the surrounding vehicles’ location information. The driving path from the starting point to the destination is obtained in advance through global planning. However, local planning is not obtained, so the ego-vehicle driving policy needs to decide how to avoid obstacles, change lanes, and choose acceleration and deceleration behaviors during the driving process.

The ego-vehicle decision problem is transformed based on reinforcement learning algorithms into a behavioral action optimization problem. Ego-vehicle driving policy replaces the IDM and MOBIL models to sends actions to the bottom tracking controller.

3. IP-SAC Algorithm Framework

3.1. Algorithm Framework Design

We first apply the Soft Actor-Critic (SAC) algorithm to ego-vehicle control. Based on SAC, we proposed IP-SAC, which not only adds an interval prediction model to predict the accessible areas of obstacle vehicles to avoid the potential collision but also adds the self-attention network to calculate the attention weight value to filter major obstacle vehicles.

The proposed IP-SAC is shown in Figure 2. At each time step, the agent interacts with the roundabout environment to obtain samples ($s, a, r, s\prime$) that are stored in the replay buffer whose capacity is set to hold one million data items. During the learning process, a minibatch with 256 data items is randomly selected from the replay buffer which is used to solve the problem of data correlation and non-stationary distribution. In addition, the algorithm is able to learn from past experiences to increase data utilization and learning efficiency. The state vector $s$ combined with the action $a$ is used as input to self-attention networks. The self-attention networks output Q values, which are used to evaluate the value of taking input action under the input state vector. The next state vector $s\prime$ is used as input to the policy network to calculate the next action. The inputs of the target networks are $s\prime$ combined with the next action. Then, the Q value at the next moment can be obtained, which evaluates the value of taking the next action under the next state. Then, self-attention networks and policy networks are trained according to Equation (11), respectively. The α is learned by dual gradient descent according to Equation (12). More details about the IP-SAC algorithm have been shown in

Table 3. Training hyperparameters and neural network structure.

Parameters	Value
pre-training steps	1000
maximum steps in a single round	500
batch size	256
replay size	1,000,000
discount factor	0.99
learning rate	0.0003
Optimizer	Adam
fully connected hidden layer	[128, 128]
Self-attention network coding layer	[64, 64]
Self-attention network decoding layer	[64, 64]
Self-attention network head	2
Self-attention network normalization factor	32

.

$${\mathit{\pi }}^{*}=\arg \underset{\pi }{\max }{\mathbb{E}}_{\left(s_t,a_t\right)~\pi }\left[{\sum }_{t}r\left({\mathit{s}}_t,{\mathit{a}}_t\right)+\alpha H(\pi (·|{\mathit{s}}_t))\right]$$

(11)

$$J\left(\alpha \right)={\mathbb{E}}_{\left(s_t,a_t\right)~\pi }\left[-\alpha \log \left(\mathsf{\pi }\left({\mathit{a}}_t|{\mathit{s}}_t\right)\right)-\alpha H\right]$$

(12)

where ${\mathit{\pi }}^{*}$ is the new policy, $\pi$ is the old policy, ${\mathbb{E}}_{\left(s_t,a_t\right)~\pi }$ is the expectation. ${\mathit{a}}_t$ is the action of the ego-vehicle at moment $t$, ${\mathit{s}}_t$ is the observed state of the environment at moment $t$, $r\left({\mathit{s}}_t,{\mathit{a}}_t\right)$ is the reward for making ${\mathit{a}}_t$ action at moment $t$, $\alpha$ is the temperature coefficient that determines the weight of entropy relative to the reward value, $H\left(\pi \left(·|{\mathit{s}}_t\right)\right)=-E_a[\log (\mathsf{\pi }({\mathit{a}}_t|{\mathit{s}}_t))]$ is the entropy of the action at policy $\pi$ the entropy value.

The IP-SAC algorithm pseudocode is shown in

Table 4. IP-SAC training process.

Interval Processor with Soft Actor-Critical, IP-SAC
Input: attention matrix, accessible area.
1:	Initialize network and parameters.
2:	for epoch iteration do:
3:	for each environment step do:
4:	Interval prediction model calculates potential feasible paths.
5:	Adjust the reward function according to the prediction results.
6:	Output action(t) according to SAC policy.
7:	After performing action(t), the environment is transferred to state(t + 1) and rewarded with reward(t).
8:	Save the training sample: sample(t) = {s(t), a(t), r(t), s(t + 1)}.
9:	A small batch of samples were randomly selected from the experience pool buffer to calculate the gradient training and update the neural network parameters.
10:	End for
11:	End for
12:	Saving network parameters.
Output: roundabout driving policy: ${\pi }_{new}^{*}$.

.

3.2. Interval Prediction Model

Ego-vehicles can obtain speed, position, and other information about the obstacle vehicles through sensors such as cameras and LIDAR, but obstacle vehicles’ intentions are not directly perceivable. For example, obstacle vehicles suddenly change lanes, accelerate, decelerate, turn left or right, etc. Therefore, uncertain behaviors of obstacle vehicles increase the safety risk of the ego-vehicle. Ego-vehicle needs to to analyze the obtained information further and predict obstacle vehicles’ behavior.

The interval prediction model calculates the obstacle vehicles’ accessible area and can predict the locations of obstacle vehicles arriving in the future fixed steps, as shown in Figure 3. The obstacle vehicles are regarded as a linear system, as Equation (13).

$$\dot{x}\left(t\right)=\mathit{A}\left(\theta \right)x\left(t\right)+\mathit{B}u\left(t\right)+\mathit{D}\omega \left(t\right), t\ge 0$$

(13)

where $x\left(t\right)$ is the state, $u\left(t\right)$ is the control, $\omega \left(t\right)$ is the sensor perturbation, and $\mathit{A}$, $\mathit{B}$, and $\mathit{D}$ are the system matrix, control matrix, and perturbation matrix, respectively.

A period of historical data $D_N={\left\{\left(x_n,y_n,u_n\right)\right\}}_{n\in \left[N\right]}$ is observed to predict the possible arrival area of other obstacle vehicles. The interval prediction result $\left[\underset{\_}{x}\left(t\right)-\overline{x}\left(t\right)\right]$ is calculated by the control signal $u:\left[t,+\infty \right)$ and the upper, and lower bounds of the state perturbation $\left[\underset{\_}{\omega }\left(t\right)-\overline{\omega }\left(t\right)\right]$, and the estimating the confidence interval $\hat{\mathsf{\Theta }}\left(t\right)$ from the current observed state. Based on the interval prediction $x\left(t_N\right)$ the obstacle vehicle arrives at the next moment at the position as Equations (14) and (15).

$$\dot{\underset{\_}{x}}\left(t\right)={\underset{\_}{\mathit{A}}}^{+}{\underset{\_}{x}}^{+}\left(t\right)-{\overline{\mathit{A}}}^{+}{\underset{\_}{x}}^{-}\left(t\right)-{\underset{\_}{\mathit{A}}}^{-}{\overline{x}}^{+}\left(t\right)+{\overline{\mathit{A}}}^{+}{\overline{x}}^{-}\left(t\right)+\mathit{B}u\left(t\right)+{\mathit{D}}^{+}\underset{\_}{\omega }\left(t\right)-{\mathit{D}}^{-}\overline{\omega }\left(t\right)$$

(14)

$$\dot{\overline{x}}\left(t\right)={\overline{\mathit{A}}}^{+}{\overline{x}}^{+}\left(t\right)-{\underset{\_}{\mathit{A}}}^{+}{\overline{x}}^{-}\left(t\right)-{\overline{\mathit{A}}}^{-}{\underset{\_}{x}}^{+}\left(t\right)+{\underset{\_}{\mathit{A}}}^{-}{\underset{\_}{x}}^{-}\left(t\right)+\mathit{B}u\left(t\right)+{\mathit{D}}^{+}\overline{\omega }\left(t\right)-{\mathit{D}}^{-}\underset{\_}{\omega }\left(t\right)$$

(15)

In the roundabout scene, yellow vehicles indicate that an interval prediction algorithm has been applied to predict their locations and driving areas. By predicting the possible reach areas, obstacle vehicles at the current location intention can be calculated, so that ego-vehicle can avoid the areas where there may occur collisions. Obstacle vehicle 1’s intention is predicted to be lane-keeping in the roundabout. According to multiple accessible areas in obstacle vehicle 2, obstacle vehicle 2’s intentions predicted that it might change lanes or drive out of the roundabout, as shown in Figure 4.

3.3. Self-Attention Network

Only some obstacle vehicles in the roundabout scenario will affect the behavior of the ego-vehicle, so it is necessary to filter obstacle vehicles that affect the ego-vehicle behavior in the current state. Ego-vehicle makes behavior decisions based on the filtered obstacle vehicles so that the ego-vehicle driving policy is more reasonable and closer to human driving behavior habits. In this paper, a self-attention network layer [20] calculated the weight of each obstacle vehicle. Via calculated weights, ego-vehicle finds out obstacle vehicles that may have conflicts with ego-vehicle. As in the framework shown in Figure 5, the feature information such as the location of obstacle vehicles is passed to the coding layer. Then, the coding layer calculates the value of each obstacle vehicle’s weight. Finally, weights are passed to the decoding layer by the Softmax function, and the decoding layer outputs the action of a behavioral decision.

The self-attention network extracts the environment information, calculates the weight coefficient according to the Query (Q) and Key (K) inputted by the coding layer, and then calculates the weighted sum of Value (V) according to the weight coefficient.

The correlation weights between obstacle vehicles ($k_i$,$v_i$) and ego-vehicle ($q_0$,$k_0$,$v_0$) is calculated separately. The scaling factor $\sqrt{d_k}$ divided the weights for normalization. Finally, output by a layer of Softmax function, as shown in Figure 6, the attention can be calculated as Equation (16).

$$output=\sigma \left(\frac{\mathit{Q}{\mathit{K}}^T}{\sqrt{d_k}}\right)\mathit{V}$$

(16)

where $\mathsf{\sigma }$ is Softmax function, $\mathit{Q}$ is State vector of the vehicle, $\mathit{K}$ is the correlation vector between this vehicle and obstacle vehicles, $\mathit{V}$ is the state vector of obstacle vehicles, $\sqrt{d_k}$ is the normalization coefficient, $d_k$ is 32.

Different widths lines represent surrounding obstacle vehicle attention weight values calculated by the self-attention network, as shown in Figure 7. Ego-vehicle calculates the weight of different obstacle vehicles. By different weights, the ego-vehicle specifies which obstacle vehicle will affect the ego-vehicle behavior. Therefore, the ego-vehicle behavioral decision-making ability in roundabout scenarios is improved.

3.4. State Action and Reward Setting

In the action setting stage, we define four actions: acceleration, slow, change left lane, and change right lane. Position, heading, and speed information of the obstacle vehicle and ego-vehicle as state space are also defined.

The reward value is determined according to the different states of the current ego-vehicle in the roundabout. The reward function is shown in

Table 5. IP-SAC reward function.

Award Category	Reward Subfunctions
Crash penalty	$r_1=\{\begin{array}{cc}\hfill -\left(10+\frac{v_t}{12}\right),& \mathrm{crashed}\\ \hfill 0,& \mathrm{otherwise}\end{array}$
Lane change penalty	$r_2=-0.5$
Collision area penalty	$r_3=-1$
Speed reward	$r_4=\frac{1}{12}*\left[-2,10\right]\propto v_t,v_t\in \left(0,12m/s\right)$
Time penalty	$r_5=-t/100$
Finish reward	$r_6=5$

. When a collision occurs between the ego-vehicle and an obstacle vehicle, the collision penalty is based on the speed of the ego-vehicle, $v_t$ is the current speed of the vehicle, and $t$ is the cumulative time step of this round. When the ego-vehicle changes lane, there will be a lane change penalty. The collision area penalty is a penalty that occurs when the ego-vehicle drives into the next moment of the other obstacle vehicle’s drive area (this area is predicted by the interval prediction algorithm). Speed reward is calculated based on ego-vehicle speed. When the ego-vehicle is driven longer, the time penalty increases. Finish reward will be given when the ego-vehicle successfully reaches its destination.

The final reward function is as Equation (17).

$$R=r_1+r_2+r_3+r_4+r_5+r_6$$

(17)

4. Simulation Results and Analysis

4.1. Simulation Test Results

Train under different random seeds and the same hyper-parameters, as shown in

Table 6. Training hyperparameters and neural network structure.

Parameters	Value
Number of training experience accumulation steps	1000
Maximum number of steps in a single round	500
Number of small batch samples	256
Update frequency	2
Playback buffer size	1e6
Discount factor	0.99
Strategy network learning rate	3e−4
Neuron activation function	ReLU
Optimizer	Adam
Fully connected hidden layer	[128, 128]
Self-attentive network coding layer	[64, 64]
Self-attentive network decoding layer	[64, 64]
Self-attentive network head count	2
Attention network normalization factor	32

. The change in the total reward value is recorded, as shown in Figure 8. The convergence of the final total reward value demonstrates the correctness of the algorithm.

As shown in Figure 8, the IDM/MOBIL converges near the total reward value of 14, the SAC policy converges near the total reward value of 18, while the IP-SAC policy converges near the total reward value of 22. The total reward value has increased by 6 and 4, and IP-SAC has increased by 22% compared with SAC, showing that IP-SAC policy performs better.

In order to compare the training effect of the IP-SAC policy, SAC and IP-SAC tested 100 rounds in easy and difficult traffic. We record the average passing speed and calculate the success and collision rates. As shown in Figure 9, the average speed of SAC policy fluctuates between 3.9–9.7 m/s each time, showing that the instability of behavioral decision-making policy is very unsafe. The IP-SAC policy makes the average speed stable between 5.9–7.5 m/s, which shows that when the surrounding environment changes, the vehicle speed can still stay the same. IP-SAC policy is more stable, and the ego-vehicle average speed fluctuation is reduced.

The two policies’ success rates are compared in the easy and difficult scenarios. The purpose is to describe the robustness of the policy and its adaptability to the difficult roundabout scenarios. As shown in Figure 10, the success rate of the SAC policy is 64%, and the IP-SAC policy is 90% in the simple traffic flow. The success rate of the SAC policy is 22%, and the IP-SAC policy is 43% in the dense traffic flow of roundabout. The results show that the success rate of IP-SAC has obvious advantages under different traffic flows roundabout. In terms of the sum of the collision and success rates of SAC and IP-SAC, the sum of the success and collision rates of the SAC policy is less than 100%. The sum of the success rate and collision rate is less than 100%, indicating that the ego-vehicle was not passed within the specified time, which is an overtime case. The sum of the success rate and collision rate of IP-SAC observation is close to 100%, which significantly reduces the occurrence of timeout.

In order to analyze the cause for timeout, the control variable method is used to separately add the interval prediction model and the self-attention network to the policy. We record the success rate and collision rate of the single method, as shown in Figure 11. Through the analysis of the success rate and collision rate of the difficult scenarios in Figure 10 and Figure 11. The sum of success rate and collision rate using interval prediction method is still not 100%. However, with the addition of the self-attention network, the policy success rate and collision rate are both close to 100%. There is only a 3% timeout in the difficult scenarios. The results show that adding the self-attention network reduces the failure of ego-vehicles to time out at the unsignalized roundabout.

The comparison result of the control variable method shows that the success rate of adding interval prediction alone and using the self-attention network in the difficult scenarios is low. However, the success rate will be increased from 20% to 43% if interval prediction and self-attention are used together. The result shows that the self-attention network and interval prediction can complement each other, reduce collisions and timeout, greatly improve the success rate, and have better performance.

4.2. Ablation Experiment

In this paper, the interval prediction model and the self-attentive network are added to the SAC. In order to investigate the effect of both on policy improvement, we randomly generate 5–15 other vehicles at each roundabout reset and compare the SAC, SAC + Interval prediction, and SAC + Self-attentive network and IP-SAC in terms of success rate, timeout, and collision rate, and investigate which method improves the policy the most, as shown in

Table 7. Results of the ablation study on different methods.

Method	Success	Collision	Timeout
SAC	0.56	0.25	0.19
SAC + Interval prediction	0.73	0.14	0.13
SAC + Self-attention network	0.72	0.22	0.06
IP-SAC	0.83	0.15	0.02

. The SAC policy has a higher collision rate and timeout situation, interval prediction reduces the collision rate and self-attentive network reduces the timeout situation. IP-SAC combines the advantages of interval prediction and self-attentive network and has a greater improvement in both collision rate and timeout situation.

The results of the ablation study are consistent with the results of the tests in simple and complex scenarios (Section 4.1), and we can conclude that interval prediction has an advantage in terms of collisions against vehicles, which can be reduced at roundabouts, and the self-attentive network can reduce vehicle failures at roundabouts due to timeouts by filtering out the vehicles from the surrounding vehicles that mainly affect this vehicle.

4.3. Visual Analysis of Simulation Output Results

We extract the simulated driving screens of SAC and IP-SAC policies, as shown in Figure 12. The simulation shows that SAC policy collisions mainly occur at the moment of roundabout merge-in and -out, while IP-SAC policy reduces the occurrence of the case.

When the ego-vehicle is running in the roundabout, there is an obstacle vehicle merging quickly on the right side. There is a potential collision between the two vehicles at the intersection. As shown in Figure 12a, the SAC policy failed to predict the behavior of obstacle vehicles at the next moment in advance and did not decelerate. Eventually the ego-vehicle collided with the obstacle vehicle. As shown in Figure 12b, in the IP-SAC policy, the ego-vehicle normally runs in the roundabout. When the obstacle vehicle on the right side drives into the roundabout quickly, the ego-vehicle predicts the next moment’s position of the obstacle vehicle on the right side and thinks that a collision may occur at the entrance of the roundabout. Therefore, the ego-vehicle changes the lane in advance to drive in the inner lane of the roundabout, leaving space for the obstacle vehicle to enter the roundabout. IP-SAC policy reduced the risk coefficient and avoided the collision between the two vehicles.

Through the two policies of the ego-vehicle for the same situation, the IP-SAC policy is more sensitive to unsignalized roundabouts at the entrance and exit. IP-SAC policy can greatly reduce the risk of collision at the entrance and exit and reduce the risk coefficient.

The continuous simulation step of IP-SAC policy entering and exiting the roundabout is shown in Figure 13. Before entering the roundabout, according to self-attention work different lines, the ego-vehicle mainly focuses on the obstacle vehicles in the roundabout. At the same time, the ego-vehicle pays little attention to other obstacle vehicles at the east and west entrances of the roundabout, and observes no obstacle vehicles at the merge port, so accelerates into the roundabout, as shown in Figure 13a. When the ego-vehicle enters the roundabout, follow the front vehicle and keep a safe distance, as shown in Figure 13b. Ego-vehicle continues to drive and pass the east merge port, paying attention to the vehicles that will enter the roundabout, as shown in Figure 13c. At the north merge port, there are obstacles vehicles to driving in and out of the roundabout, so the ego-vehicle drives carefully, as shown in Figure 13d. When the north obstacle vehicle quickly enters the roundabout, the ego-vehicle decelerates, as shown in Figure 13e. After there is no obstacle vehicle in front of the ego-vehicle, the ego-vehicle starts to accelerate, as shown in Figure 13f. When the ego-vehicle is about to leave the roundabout, it still pays attention to the surrounding vehicles, as shown in Figure 13g. When completely out of the roundabout, the ego-vehicle will not pay attention to other obstacle vehicles in the roundabout, as shown in Figure 13h.

To sum up, the IP-SAC behavioral decision-making policy can filter other obstacle vehicles that do not affect the current ego-vehicle behavior in the unsignalized roundabout, and the ego-vehicle focuses on the surrounding obstacle vehicles that may cause conflicts.

4.4. Verify in CARLA

We deploy the IP-SAC trained model in the CARLA high-dimensional environment. First, we added other obstacle vehicles to CARLA to simulate roundabout traffic flow, as shown in Figure 14. Second, we use the LIDAR and the front camera to percept the surrounding vehicles and project the obstacle vehicles’ location onto the map. Eventually, the relative positions of other obstacle vehicles fed into the IP-SAC driving policy to generate ego-vehicle actions and control the ego-vehicle.

We recorded the ego-vehicle front camera and LiDAR data, perception extraction information, and speed curves of the ego-vehicle driving in the traffic circle, as shown in Figure 15. The results showed that the vehicle drove safely out of the roundabout without collision. We extracted six moments of ego-vehicle driving data: (1) the ego-vehicle start, (2) the ego-vehicle enters the roundabout, (3) when there is an obstacle vehicle on the right side of the ego-vehicle, (4) ego-vehicle slowing down to avoid the obstacle vehicle, (5) ego-vehicle accelerate to continue driving, (6) ego-vehicle drive out of the roundabout.

5. Discussions

In this section, we compare our experimental results with recent research on the application of reinforcement learning to roundabouts and discuss the sim2real problem, the limitations of our approach, and future research directions. Compared to the Q-learning method this paper has the advantage of using a more advanced algorithm (SAC), Laura et al. [14]. simply added one other vehicle or no other vehicles were involved and just drove through the roundabout, in this paper, multiple obstacle vehicles have been added to the roundabout to more closely resemble a real-life scenario and to test policy decisions. Hyunki Seong et al. [23]. combine a self-attentive network with SAC. This paper compares this method to the IP-SAC method on the same platform and in the same environment, resulting in a 15% improvement in collision rate due to the inclusion of an interval prediction model, as shown in Table 7.

However, the limitation of this paper is that firstly, the algorithm is verified inside the simulation environment, and the obstacle vehicles’ position is input to the policy network as sensing results in Highway-Env and CARLA, without combining with advanced sensing algorithms. Secondly, considering the sim2real (simulation to reality) problem, there is still a gap between the simulation environment and reality. We refer to the problems encountered by robots, robotic arms, and autonomous vehicles using reinforcement learning in both real and simulated environments, where direct interactive training in a real environment would be too inefficient in terms of sampling and safety issues. Reinforcement learning can have tens of millions of samples in training, and sampling in the real-world environment can be very time-consuming. Secondly, there is the issue of safety. As reinforcement learning is constantly subject to trial and error during training, robotic arms and robots may be damaged and collide with other objects, and vehicles may face more serious collisions and even harm to drivers. However, if training is carried out in a simulation environment, there will be errors in the modeling of the simulation environment, and it is impractical to deploy the trained policies directly into the real environment. To address the sim2real problem, we thought that the simulation environment can be randomized as much as possible, such as weather, vehicle color, road conditions, etc., and mixed simulations with real data for training. Alternatively, sensing and decision-making can be separated. In this paper, the policy inputs information about vehicle location parameters and does not directly input sensor data such as camera and LIDAR into the policy network, which we believe can reduce the impact of sim2real.

Although CARLA is very close to the real scenario, the effects of policy generalization, road conditions, weather, and perceptual noise are not taken into account, which is also a challenge for the deployment of deep reinforcement learning in autonomous driving decision-making today. This challenge must be addressed both in the simulation environment and in the deployment of real vehicles, where the simulation environment is continuously optimized to be close to the real scenario and the trained policies are deployed on advanced autonomous vehicle systems for validation before reinforcement learning can be truly applied to autonomous driving.

In the future, we will train the IP-SAC policy on a variety of scenarios such as a five-legged or three-legged roundabout, and intersections to obtain a more generalized decision policy. In the meantime, this can be combined with other advanced research, such as the program developed by Maria Rella Riccardi et al. [24] for the evaluation of safety factors at urban roundabouts, an active calculation of the road Safety Index (SI). We can explore the correlation between the collision locations of the ego-vehicle in training and the prediction of collisions based on the SI values of the roads. It is also possible to combine reinforcement learning with this type of active safety approach by using the road SI values as input to the network along with vehicle location information and training them using reinforcement learning algorithms. This can be compared to a method that only inputs vehicle location information to verify that the collision rate can be further reduced to improve vehicle safety.

6. Conclusions

In this paper, aiming at the complex unsignalized roundabout, we first use a reinforcement learning algorithm (SAC) to control the autonomous vehicle drive in the unsignalized roundabout scenario. Second, we propose an autonomous driving policy (IP-SAC). Third, the algorithmic policy model is validated in a low-dimensional environment. The simulation result shows that the IP-SAC behavioral decision policy has good decision ability and can reduce conflicts and collisions in the unsignalized roundabout. IP-SAC reduces the risk factor of ego-vehicle at roundabout entrances and exits, reduces the waiting time before entering the roundabout, improves the success rate, and reduces the fluctuation of the average speed. Finally, to further test the effectiveness of the IP-SAC policy, the policy is deployed to the CARLA environment. The speed profile of the ego-vehicle driving in the traffic circle was recorded. The verification results show that IP-SAC can make this vehicle drive safely out of the roundabout.

In summary, the IP-SAC policy has better behavioral decision capability, better stability, and a higher scenario task success rate in complex scenarios. In the future, we expect that IP-SAC can be deployed in real-world urban driving.