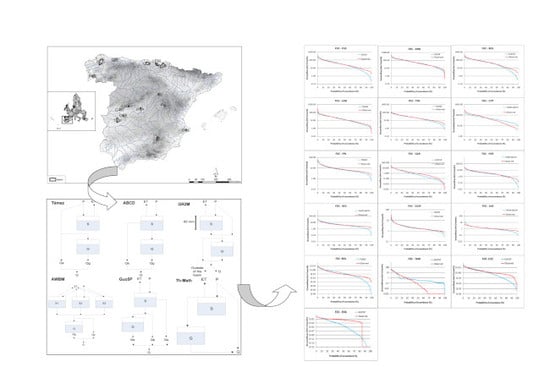
Evaluating Hydrological Models for Deriving Water Resources in Peninsular Spain
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data
2.2. Methodology
2.2.1. Water Balance Models
Témez Model
ABCD Model
GR2M-1994 Model (GR4-1994)
AWBM Model
Guo Model (Five Parameters)
Thornthwaite-Mather Model
2.2.2. Goodness-of-Fit Tests
3. Results
3.1. Precipitation Data Series Assessment
3.2. Models’ Parameters
3.3. Goodness-of-Fit Tests
3.3.1. AIC and BIC Criteria
3.3.2. Grading Classification (NSE, PBIAS, R2)
4. Discussion
4.1. Water Volume Assessment (REV)
4.2. Model Selection
4.3. Models Uncertainty Analysis
4.4. Flow Duration Curves
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Témez Model
Appendix B. ABCD Model
Appendix C. GR2M
Appendix D. AWBM
Appendix E. Guo-5P
Appendix F. Thornthwaite-Mather
References
- Wurbs, R.A. Texas water availability modeling system. J. Water Resour. Plan. Manag. 2005, 131, 270–279. [Google Scholar] [CrossRef]
- Senent-Aparicio, J.; Liu, S.; Pérez-Sánchez, J.; López-Ballesteros, A.; Jimeno-Sáez, P. Assessing Impacts of Climate Variability and Reforestation Activities on Water Resources in the Headwaters of the Segura River Basin (SE Spain). Sustainability 2018, 10, 3277. [Google Scholar] [CrossRef]
- Puricelli, M.M. Estimación y Distribución de Parámetros del Suelo Para la Modelación Hidrológica. Ph.D. Thesis, Departamento de Ingeniería Hidráulica y Medio Ambiente, Universidad Politécnica de Valencia, Valencia, Spain, 2003. [Google Scholar]
- Essam, M. Water Flow and Chemical Transport in a Subsurface Drained Watershed. Ph.D. Thesis, University of Illinois, Champaign County, IL, USA, 2007. [Google Scholar]
- Shimon, C. Water Resources; Island Press: Washington, DC, USA, 2010. [Google Scholar]
- Unesco. Methods for Water Balance Computation; Instituto de Hidrología de España: Madrid, Spain, 1981. [Google Scholar]
- Thornthwaite, C.W. A new and improved classification of climates. Geogr. Rev. 1948, 38, 55–94. [Google Scholar] [CrossRef]
- Thornthwaite, C.W.; Mather, J.R. Instructions and Tables for Computing Potential Evapotranspiration and the Water Balance; Publications in Climatology; Drexel Institute of Technology, Laboratory of Climatolog: Centerton, NJ, USA, 1957; Volume 10. [Google Scholar]
- Alley, W.M. On the treatment of evapotranspiration, soil moisture accounting, and aquifer recharge in monthly water balance models. Water Resour. Res. 1984, 20, 1137–1149. [Google Scholar] [CrossRef]
- Xiong, L.; Guo, S. A two-parameter monthly water balance model and its application. J. Hydrol. 1999, 216, 111–123. [Google Scholar] [CrossRef]
- Makhlouf, Z.; Michel, C. A two-parameter monthly water balance model for French watersheds. J. Hydrol. 1994, 162, 299–318. [Google Scholar] [CrossRef]
- Giakoumakis, S.; Tsakiris, G.; Efremides, D. On the Rainfall-Run-Off Modelling in a Mediterranean Island Environment; Advances in Water Resources Technology; Tsakiris, G., Ed.; Balkema: Rotterdam, The Netherlands, 1991. [Google Scholar]
- Mimikou, M.A.; Hadjisawa, P.S.; Kouvopoulos, Y.S.; Afrateos, H. Regional climate change impacts: II. Impacts on water management works. Hydrol. Sci. J. 1991, 36, 259–270. [Google Scholar] [CrossRef]
- Alley, W.M. Water balance models in one-month-ahead streamflow forecasting. Water Resour. Res. 1985, 21, 597–606. [Google Scholar] [CrossRef]
- Abulohom, M.S.; Shah, S.M.S.; Ghumman, A.R. Development of a rainfall-run-off model, its calibration and validation. Water Resour. Manag. 2001, 15, 149–163. [Google Scholar] [CrossRef]
- Yates, D.; Strzepek, K. Modeling the Nile basin under climate change. J. Hydrol. Eng. 1998, 3, 98–108. [Google Scholar] [CrossRef]
- Vandewiele, G.; Xu, C.-Y. Methodology and comparative study of monthly water balance models in Belgium, China and Burma. J. Hydrol. 1992, 134, 315–347. [Google Scholar] [CrossRef]
- Andréassian, V.; Hall, A.; Chahinian, N.; Schaake, J. Introduction and Synthesis: Why Should Hydrologists Work on A Large Number of Basin Data Sets? In Large Sample Basin Experiments for hydrological Model Parameterization, Results of the Model Parameter Experiment—MOPEX; IAHS Publication No. 307; IAHS Press: Paris, France, 2006. [Google Scholar]
- Perrin, C.; Michel, C.; Andreassian, V. Does a large number of parameters enhance model performance? Comparative assessment of common catchment model structures on 429 catchments. J. Hydrol. 2001, 242, 275–301. [Google Scholar] [CrossRef]
- Chiew, F.H.S.; McMahon, T.A. Australian Data for Rainfall-Run-Off Modelling and the Calibration of Models Against Streamflow Data Recorded Over Different Time Periods; Civil Engineering Transactions, The Institution of Engineers: Sydney, Australia, 1993; Volume 35, pp. 261–274. [Google Scholar]
- World Meteorological Organization. Intercomparison of Conceptual Models Used in Operational Forecasting; Operational Hydrology Report No. 7, WMO-No. 429; WMO: Geneva, Switzerland, 1975. [Google Scholar]
- Xu, C.Y.; Singh, V.P. Dependence of evaporation on meteorological variables at different time-scales and intercomparison of estimation methods. Hydrol. Process. 1998, 12, 429–442. [Google Scholar] [CrossRef]
- Todini, E. Rainfall-runoff modeling—past present and future. J. Hydrol. 1998, 100, 341–352. [Google Scholar] [CrossRef]
- Chiew, F.H.S.; Kirono, D.G.C.; Kent, D.M.; Frost, A.J.; Charles, S.P.; Timbal, B.; Nguyen, K.C.; Fu, G. Comparison of run-off modelled using rainfall from different downscaling methods for historical and future climates. J. Hydrol. 2010, 387, 10–23. [Google Scholar] [CrossRef]
- Zhang, Q.; Liu, J.; Singh, V.P.; Gu, X.; Chen, X. Evaluation of impacts of climate change and human activities on streamflow in the Poyang Lake basin, China. Hydrol. Process. 2016, 30, 2562–2576. [Google Scholar] [CrossRef]
- Wang, D.; Tang, Y. A one-parameter Budyko model for water balance captures emergent behavior in Darwinian hydrologic models. Geophys. Res. Lett. 2014, 41, 4569–4577. [Google Scholar] [CrossRef]
- Sankarasubramanian, A.; Vogel, R.M. Annual hydroclimatology of the United States. Water Resour. Res. 2002, 38, 19-1–19-2. [Google Scholar] [CrossRef]
- Lacombe, G.; Ribolzi, O.; De Rouw, A.; Pierret, A.; Latsachak, K.; Silvera, N.; Dinh, R.P.; Orange, D.; Janeau, J.L.; Soulileuth, B.; et al. Contradictory hydrological impacts of afforestation in the humid tropics evidenced by long-term field monitoring and simulation modelling. Hydrol. Earth Syst. Sci. 2016, 20, 2691–2704. [Google Scholar] [CrossRef]
- Mouelhi, S.; Michel, C.; Perrin, C.; Andreassian, V. Stepwise development of a two parameter monthly water balance model. J. Hydrol. 2006, 318, 200–214. [Google Scholar] [CrossRef]
- Burnash, R.J.C.; Ferral, R.L.; Maguire, R.A. A Generalized Streamflow Simulation System: Conceptual Models for Digital Computers; Joint Federal State River Forecast Center: Sacramento, CA, USA, 1973.
- Guo, S. Impact of Climate Change on Hydrological Balance and Water Resource Systems in the Dongjiang Basin, China; Modeling and Management of Sustainable Basin-Scale Water Resource Systems (Proceedings of a Boulder Symposium); LAHS Publ.: Los Alamos, NM, USA, 1995; Volume 231. [Google Scholar]
- Singh, K.; Kumar, A. Evaluation of relief aspects morphometric parameters derived from different sources of DEMs and its effects over time of concentration of run-off (TC). Earth Sci. Inform. 2016. [Google Scholar] [CrossRef]
- Singh, S.K. Transmuting synthetic unit hydrograph into gamma distribution. J. Hydrol. Eng. 2000, 5, 380–385. [Google Scholar] [CrossRef]
- Ferrer, J. Recomendaciones para el Cálculo Hidrometeorológico de Avenidas; CEDEX M-37, CEDEX: Madrid, Spain, 1993. [Google Scholar]
- Témez, J.R. Extended and Improved Rational Method: Version of the Highways Administration of Spain. In Proceedings of the XXIV Congress of IAHR, Madrid, Spain, 9–13 September 1991; Volume A, pp. 33–40. [Google Scholar]
- Témez, J.R. Cálculo Hidrometeorológico de Caudales Máximos en Pequeñas Cuencas Naturales; Dirección General de Carreteras, MOPU: Madrid, Spain, 1987.
- Lyon, S.W.; Walter, M.T.; Gerard-Marchant, P.; Steenhuis, T.S. Using a topographic index to distribute variable source area run-off predicted with the SCS curve-number equation. Hydrol. Proc. 2004, 18, 2757–2771. [Google Scholar] [CrossRef]
- Frankenberger, J.R.; Brooks, E.S.; Walter, M.T.; Walter, M.F.; Steenhuis, T.S. A GIS-Based Variable Source Area Hydrology Model. Hydrol. Process. 1999, 13, 804–822. [Google Scholar] [CrossRef]
- Calvo, J.C. An evaluation of Thornthwaite’s water balance technique in predicting stream run-off in Costa Rica. Hydrol. Sci. J. 1986, 31, 51–60. [Google Scholar] [CrossRef]
- Croke, B.F.W.; Andrews, F.; Jakeman, A.J.; Cuddy, S.M.; Luddy, A. IHACRES classic plus: A redesign of the IHACRES rainfall-run-off model. Environ. Model. Softw. 2006, 21, 426–427. [Google Scholar] [CrossRef]
- Chiew, F.H.S.; McMahon, T.A. Modelling the impacts of climate change on Australian streamflow. Hydrol. Process. 2002, 16, 1235–1245. [Google Scholar] [CrossRef]
- Perrin, C.; Michel, C.; Andréassian, V. Improvement of a parsimonious model for streamflow simulation. J. Hydrol. 2003, 279, 275–289. [Google Scholar] [CrossRef]
- Boughton, W. New approach to calibration of the AWBM for use on ungauged catchments. J. Hydrol. Eng. 2009, 14, 562–568. [Google Scholar] [CrossRef]
- Boughton, W. Effect of data length on rainfall–run-off modelling. Environ. Model. Softw. 2007, 22, 406–413. [Google Scholar] [CrossRef]
- Boughton, W. Calibrations of a daily rainfall–run-off model with poor quality data. Environ. Model. Softw. 2006, 21, 1114–1128. [Google Scholar] [CrossRef]
- Boughton, W. The Australian Water Balance Model. Environ. Model. Softw. 2004, 19, 943–956. [Google Scholar] [CrossRef]
- Boughton, W.; Chiew, F. Estimating run-off in ungauged catchments from rainfall, PET and the AWBM model. Environ. Model. Softw. 2007, 22, 476–487. [Google Scholar] [CrossRef]
- O’Connell, P.E.; Nash, J.E.; Farrell, J.P. River flow forecasting through conceptual models, Part 2, The Brosna catchment at Ferbane. J. Hydrol. 1970, 10, 317–329. [Google Scholar] [CrossRef]
- Singh, V.P. Watershed Modeling. In Computer Models of Watershed Hydrology, 1st ed.; Water Resources Publications: Highlands Ranch, CO, USA, 1995. [Google Scholar]
- Singh, V.P.; Frevert, D.K. Mathematical Models of Small Watershed Hydrology and Applications; Water Resources Publications: Littleton, CO, USA, 2002. [Google Scholar]
- Eder, G.; Fuchs, M.; Nachtnebel, H.; Loibl, W. Semi-distributed modelling of the monthly water balance in an alpine catchment. Hydrol. Process. 2005, 19, 2339–2360. [Google Scholar] [CrossRef]
- Arnold, J.G.; Srinivasan, R.; Muttiah, R.S.; Williams, J.R. Large-area hydrologic modeling and assessment: Part I. Model development. J. Am. Water Resour. Assoc. 1998, 34, 73–89. [Google Scholar] [CrossRef]
- Beven, K.J. Rainfall-Run-off Modelling: The Primer; Wiley: Chichester, UK, 2001. [Google Scholar]
- Ewen, J.; Parkin, G. Validation of catchment models for prediction land use and climate change impact. 1. Method. J. Hydrol. 1996, 175, 583–594. [Google Scholar] [CrossRef]
- Carpenter, T.M. Discretization scale dependencies of the ensemble flow range versus catchment area relationship in distributed hydrologic modeling. J. Hydrol. 2006, 328, 242–257. [Google Scholar] [CrossRef]
- Viney, N.R.; Croke, B.F.W.; Breuer, L.; Bormann, H.; Bronstert, A.; Frede, H.; Gräff, T.; Hubrechts, L.; Huisman, J.A.; Jakeman, A.J.; et al. Ensemble modelling of the hydrological impacts of land use change. In Proceedings of the MODSIM05—International Congress on Modelling and Simulation: Advances and Applications for Management and Decision Making, Melbourne, Australia, 12–15 December 2005; Zerger, A., Argent, R.M., Eds.; ANU: Canberra, Australia, 2005; pp. 2967–2973. [Google Scholar]
- Croke, B.F.W.; Merritt, W.S.; Jakeman, A.J. A dynamic model for predicting hydrologic response to land cover changes in gauged and ungauged catchments. J. Hydrol. 2004, 291, 115–131. [Google Scholar] [CrossRef]
- Vansteenkiste, T.; Tavakoli, M.; Ntegeka, V.; De Smedt, F.; Batelaan, O.; Pereira, F.; Willems, P. Intercomparison of hydrological model structures and calibration approaches in climate scenario impact projections. J. Hydrol. 2014, 519, 743–755. [Google Scholar] [CrossRef]
- Samaniego, L.; Kumar, R.; Attinger, S. Multiscale parameter regionalization of a grid--based hydrologic model at the mesoscale. Water Resour. Res. 2010, 46, W05523. [Google Scholar] [CrossRef]
- Beck, H.E.; van Dijk, A.I.J.M.; de Roo, A.; Miralles, D.G.; McVicar, T.R.; Schellekens, J.; Bruijnzeel, L.A. Global-scale regionalization of hydrologic model parameters. Water Resour. Res. 2016, 52, 3599–3622. [Google Scholar] [CrossRef]
- Yang, X.; Michel, C. Flood forecasting with a watershed model: A new method of parameter updating. Hydrol. Sci. J. 2000, 45, 537–546. [Google Scholar] [CrossRef]
- Cameron, D.S.; Beven, K.J.; Tawn, J.; Blazkova, S.; Naden, P. Flood frequency estimation by continuous simulation for a gauged upland catchment (with uncertainty). J. Hydrol. 1999, 219, 169–187. [Google Scholar] [CrossRef]
- Uhlenbrock, S.; Seibert, J.; Leibundgut, C.; Rohde, A. Prediction uncertainty of conceptual rainfall-run-off models caused by problems in identifying model parameters and structure. Hydrol. Sci. J. 1999, 44, 779–797. [Google Scholar] [CrossRef]
- Yang, X.; Parent, E.; Michel, C.; Roche, P.A. Comparison of real-time reservoir operation techniques. J. Water Resour. Plan. Manag. 1995, 121, 345–351. [Google Scholar] [CrossRef]
- Lobligeois, F.; Andréassian, V.; Perrin, C.; Tabary, P.; Loumagne, C. When does higher spatial resolution rainfall information improve streamflow simulation? An evaluation on 3620 flood events. Hydrol. Earth Syst. Sci. 2013, 10, 12485–12536. [Google Scholar] [CrossRef]
- Smith, M.B.; Koren, V.; Zhang, Z.; Zhang, Y.; Reed, S.M.; Cui, Z.; Moreda, F.; Cosgrove, B.A.; Mizukami, N.; Anderson, E.A. Results of the DMIP 2 Oklahoma experiments. J. Hydrol. 2012, 418–419, 17–48. [Google Scholar] [CrossRef]
- Apip; Sayama, T.; Tachikawa, Y.; Takara, K. Spatial lumping of a distributed rainfall sediment-run-off model and its effective lumping scale. Hydrol. Process. 2012, 26, 855–871. [Google Scholar] [CrossRef]
- Breuer, L.; Huisman, J.A.; Willems, P.; Bormann, H.; Bronstert, A.; Croke, B.F.W.; Frede, H.-G.; Gräff, T.; Hubrechts, L.; Jakeman, A.J.; et al. Assessing the impact of land use change on hydrology by ensemble modeling (LUCHEM) I: Model intercomparison of current land use. Adv. Water Resour. 2009, 32, 129–146. [Google Scholar] [CrossRef]
- Zhang, Z.; Koren, V.; Smith, M.; Reed, S.; Wang, D. Use of next generation weather radar data and basin disaggregation to improve continuous hydrograph simulations. J. Hydrol. Eng. 2004, 9, 103–115. [Google Scholar] [CrossRef]
- Koren, V.; Reed, S.; Smith, M.; Zhang, Z.; Seo, D.J. Hydrology laboratory research modeling system (HL-RMS) of the US national weather service. J. Hydrol. 2004, 291, 297–318. [Google Scholar] [CrossRef]
- Ajami, N.K.; Gupta, H.; Wagener, T.; Sorooshian, S. Calibration of a semidistributed hydrologic model for streamflow estimation along a river system. J. Hydrol. 2004, 298, 112–135. [Google Scholar] [CrossRef]
- Reed, S.; Koren, V.; Smith, M.B.; Zhang, Z.; Moreda, F.; Seo, D.; Dmipparticipants, A. Overall distributed model intercomparison project results. J. Hydrol. 2004, 298, 27–60. [Google Scholar] [CrossRef]
- Boyle, D.P.; Gupta, H.V.; Sorooshian, S.; Koren, V.; Zhang, Z.; Smith, M. Toward improved streamflow forecasts: Value of semidistributed modeling. Water Resour. Res. 2001, 37, 2749–2759. [Google Scholar] [CrossRef]
- Refsgaard, J.C.; Knudsen, J. Operational validation and intercomparison of different types of hydrological models. Water Resour. Res. 1996, 32, 2189–2202. [Google Scholar] [CrossRef]
- Shah, S.M.S.; O’Connell, P.E.; Hosking, J.R.M. Modelling the effects of spatial variability in rainfall on catchment response. 2. Experiments with distributed and lumped models. J. Hydrol. 1996, 175, 89–111. [Google Scholar] [CrossRef]
- Bormann, H.; Breuer, L.; Giertz, S.; Huisman, J.A.; Viney, N.R. Spatially explicit versus lumped models in catchment hydrology—Experiences from two case studies. In Uncertainties in Environmental Modelling and Consequences for Policy Making. NATO Science for Peace and Security Series C: Environmental Security; Baveye, P.C., Laba, M., Mysiak, J., Eds.; Springer: Dordrecht, The Netherlands, 2009. [Google Scholar]
- Vansteenkiste, T.; Tavakoli, M.; Van Steenbergen, N.; De Smedt, F.; Batelaan, O.; Pereira, F.; Willems, P. Intercomparison of five lumped and distributed models for catchment run-off and extreme flow simulation. J. Hydrol. 2014, 511, 335–349. [Google Scholar] [CrossRef]
- Martínez-Santos, P.; Andreu, J.M. Lumped and distributed approaches to model natural recharge in semiarid karst aquifers. J. Hydrol. 2010, 388, 389–398. [Google Scholar] [CrossRef]
- Haque, M.M.; Rahman, A.; Hagare, D.; Kibria, G.; Karim, F. Estimation of catchment yield and associated uncertainties due to climate change in a mountainous catchment in Australia. Hydrol. Process. 2015, 29, 4339–4349. [Google Scholar] [CrossRef]
- Jiang, T.; Chen, Y.Q.; Xu, C.Y.; Chen, X.H.; Chen, X.; Singh, V.P. Comparison of hydrological impacts of climate change simulated by six hydrological models in the Dongjiang Basin, South China. J. Hydrol. 2007, 336, 316–333. [Google Scholar] [CrossRef]
- Kumar, A.; Singh, R.; Jena, P.P.; Chatterjee, C.; Mishra, A. Identification of the best multi-model combination for simulating river discharge. J. Hydrol. 2015, 525, 313–325. [Google Scholar] [CrossRef]
- Van Esse, W.R.; Perrin, C.; Booij, M.J.; Augustijn, D.C.M.; Fenicia, F.; Kavetski, D.; Lobligeois, F. The influence of conceptual model structure on model performance: A comparative study for 237 French catchments. Hydrol. Earth Syst. Sci. 2013, 17, 4227–4239. [Google Scholar] [CrossRef]
- Velázquez, J.A.; Anctil, F.; Perrin, C. Performance and reliability of multimodel hydrological ensemble simulations based on seventeen lumped models and a thousand catchments. Hydrol. Earth Syst. Sci. 2010, 14, 2303–2317. [Google Scholar] [CrossRef]
- Broderick, C.; Matthews, T.; Wilby, R.L.; Bastola, S.; Murphy, C. Transferability of hydrological models and ensemble averaging methods between contrasting climatic periods. Water Resour. Res. 2016, 52, 8343–8373. [Google Scholar] [CrossRef]
- Bourgin, F.; Andréassian, V.; Perrin, C.; Oudin, L. Transferring global uncertainty estimates from gauged to ungauged catchments. Hydrol. Earth Syst. Sci. 2015, 19, 2535–2546. [Google Scholar] [CrossRef]
- Ye, W.; Bates, B.; Viney, N.; Sivapalan, M.; Jakeman, A. Performance of conceptual rainfall-run-off, models in low-yielding ephemeral catchments. Water Resour. Res. 1997, 33, 153–166. [Google Scholar] [CrossRef]
- Kirchner, J.W. Getting the right answers for the right reasons: Linking measurements, analyses, and models to advance the science of hydrology. Water Resour. Res. 2006, 42, W03S04. [Google Scholar] [CrossRef]
- Escriva-Bou, A.; Pulido-Velazquez, M.; Pulido-Velazquez, D. Economic value of climate change adaptation strategies for water management in Spain’s Jucar basin. J. Water Res. Plan. ASCE 2017, 143, 04017005. [Google Scholar] [CrossRef]
- MIMAM, Libro Blanco del Agua en España; Centro de Publicaciones del Ministerio de Medio Ambiente: Madrid, Spain, 2000.
- Cabezas, F.; Estrada, F.; Estrela, T. Algunas contribuciones técnicas del Libro Blanco del Agua en España. Ingeniería Civil 1999, 115, 79–96. [Google Scholar]
- Estrela, T.; Cabezas, F.; Estrada, F. La evaluación de los recursos hídricos en el libro blanco del agua en España. Ingeniería del Agua 1999, 6, 125–138. [Google Scholar] [CrossRef]
- Estrela, T. Modelos Matemáticos para la Evaluación de Recursos Hídricos; Centro de Estudios Hidrográficos y Experimentación de Obras Públicas, CEDEX: Madrid, Spain, 1992. [Google Scholar]
- Fernandez, W.; Vogel, R.; Sankarasubramanian, A. Regional calibration of a watershed model. Hydrol. Sci. J. 2000, 45, 689–707. [Google Scholar] [CrossRef]
- Martinez, G.F.; Gupta, H.V. Toward improved identification of hydrological models: A diagnostic evaluation of the “abcd” monthly water balance model for the conterminous United States. Water Resour. Res. 2010, 46, W08507. [Google Scholar] [CrossRef]
- Sankarasubramanian, A.; Vogel, R.M. Hydroclimatology of the continental United States. Geophys. Res. Lett. 2003, 30. [Google Scholar] [CrossRef]
- Thomas, H. Improved Methods for National Water Assessment; Report WR15249270; US Water Resource Council: Washington, DC, USA, 1981.
- Pellicer-Martinez, F.; Martínez-Paz, J.M. Contrast and transferability of parameters of lumped water balance models in the Segura River Basin (Spain). Water Environ. J. 2015, 29, 43–50. [Google Scholar] [CrossRef]
- Coron, L.; Thirel, G.; Delaigue, O.; Perrin, C.; Andréassian, V. The Suite of Lumped GR Hydrological Models in an R Package. Environ. Model. Softw. 2017, 94, 166–171. [Google Scholar] [CrossRef]
- Wriedt, G.; Bouraoui, F. Towards A General Water Balance Assessment of Europe; Joint Research Centre—Institute for Environment and Sustainability, Office for Official Publications of the European Communities: Luxembourg, 2009. [Google Scholar]
- Sharifi, F.A.S.; Safarpour, S.; Ayubzadeh, S.A. Evaluation of AWBM 2002 simulation model in 6 Iranian representative catchments. Pajouhesh-Va-Sazandegi. Nat. Resour. 2004, 17, 35–42. [Google Scholar]
- Sharafi, F.; Adamowski, J.; Barkhordari, J.; Saadat, H. Decision Support Tool for Evaluating Changes in Arid and Tropical Watersheds. J. Agric. Eng. 2012, 49, 33. [Google Scholar]
- Makungo, R.; Odiyo, J.O.; Ndiritu, J.G.; Mwaka, N. Rainfall-run-off modelling approach for ungauged catchments: A case study of Nzhelele River subquaternary catchment. Phys. Chem. Earth 2010, 35, 596–607. [Google Scholar] [CrossRef]
- Peranginangin, N.; Sakthivadievel, R.; Scott, N.R.; Kendy, E.; Steenhuis, T.S. Water accounting for conjunctive groundwater/surface water management: Case of the Singkarak-Ombilin River basin, Indonesia. J. Hydrol. 2004, 292, 1–22. [Google Scholar] [CrossRef]
- Barros, R.; Isidoro, D.; Aragüés, R. Long-term water balances in La Violada irrigation district (Spain): I. Sequential assessment and minimization of closing errors. Agric. Water Manag. 2011, 102, 35–45. [Google Scholar] [CrossRef]
- Sharifi, M.A.; Rodriguez, E. Design and development of a planning support system for policy formulation in water resources rehabilitation: The case of Alcázar De San Juan District in Aquifer 23, La Mancha, Spain. J. Hydroinform. 2002, 4, 157–175. [Google Scholar] [CrossRef]
- Estrela, T.; Sahuquillo, A. Modeling the Response of a Karstic Spring at Arteta Aquifer in Spain. Groundwater 1997, 35, 18–24. [Google Scholar] [CrossRef]
- Donker, N. WTRBLN, a computer program to calculate water balance. Comput. Geosci. 1987, 13, 95–122. [Google Scholar] [CrossRef]
- Pulido-Velázquez, D.; Ahlfeld, D.; Andreu, J.; Sahuquillo, A. Reducing the computational cost of unconfined groundwater flow in conjunctive-use models at basin scale assuming linear behaviour: The case of Adra- Campo de Dalías. J. Hydrol. 2008, 353, 159–174. [Google Scholar] [CrossRef]
- Pulido-Velazquez, D.; Sahuquillo, A.; Andreu, J.; Pulido-Velazquez, M. An efficient conceptual model to simulate surface water body-aquifer interaction in Conjunctive Use Management Models. Water Resour. Res. 2007, 43, W07407. [Google Scholar] [CrossRef]
- Köppen, W. Das Geographische System der Klimate, Handbuch der Klimatologie, 1; Köppen, W., Geiger, R., Eds.; Borntraeger: Berlin, Germany, 1936. [Google Scholar]
- Köppen, W. Klassification der KlimatenachTemperatur, Niederschlag and Jahreslauf; Petermanns Geographische Mitteilungen: Gotha, Germany, 1918; pp. 193–203, 243–248. [Google Scholar]
- Köppen, W. Die Wärmezonen der Erde, nach der Dauer der heissen, gemässigten und kaltenZeit und nach der Wirkung der Wärme auf die organische Welt betrachtet. Meteorol. Z. 1884, 1, 5–226. [Google Scholar]
- UNEP (United Nations Environment Programme). World Atlas of Desertification, 2nd ed.; UNEP: London, UK, 1997. [Google Scholar]
- Álvarez, J.; Sanchez, A.; Quintas, L. SIMPA, a GRASS based Tool for Hydrological Studies. Int. J. Geo-Inf. 2005, 1, 1. [Google Scholar]
- Estrela, T.; Quintas, L. A distributed hydrological model for water resources assessment in large basins. In Proceedings of the Rivertech ’96-1st International Conference on New/Emerging Concepts for Rivers, Chicago, IL, USA, 22–26 September 1996; Volumes 1–2, pp. 861–868. [Google Scholar]
- Pérez-Martín, M.A.; Estrela, T.; Andreu, J.; Ferrer, J. Modeling water resources and river-aquifer interaction in the Júcar River basin. Spain. Water Resour. Manag. 2014, 28, 4337–4358. [Google Scholar] [CrossRef]
- Gonzalez-Zeas, D. Análisis Hidrológico de los Escenarios de Cambio Climático en España. Ph.D. Thesis, Technical Universtiy of Madrid, Madrid, Spain, 2010. [Google Scholar]
- Belmar, O.; Velasco, J.; Martinez-Capel, F. Hydrological classification of natural flow regimes to support environmental flow assessments in intensively regulated Mediterranean rivers, Segura River basin (Spain). J. Environ. Manag. 2011, 47, 992–1004. [Google Scholar] [CrossRef]
- eea.europa.eu [Internet]. European Environmental Agency, 2019. Available online: https://www.eea.europa.eu/publications/COR0-landcover (accessed on 10 February 2019).
- ign.es [Internet]. Instituto Geográfico Nacional, 2019. Available online: http://www.ign.es/web/ign/portal (accessed on 12 February 2019).
- Akaike, H. Information theory and an extension of the maximum likelihood principle. In Proceedings of the 2nd International Symposium on Information Theory, USSR, Tsahkadsor, Armenia, 2–8 September 1971; Petrov, B.N., Csáki, F., Eds.; Akadémiai Kiadó: Budapest, Hungary, 1973; pp. 267–281. [Google Scholar]
- Akaike, H. A new look at the statistical model identification. IEEE Trans. Autom. Control 1974, 19, 716–723. [Google Scholar] [CrossRef]
- Fabozzi, F.J.; Focardi, S.M.; Svetlozar, T.; Bala, G. The Basics of Financial Econometrics: Tools, Concepts, and Asset Management Applications; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2014. [Google Scholar]
- Moriasi, D.N.; Gitau, M.W.; Pai, N.; Daggupati, P. Hydrologic and Water Quality Models: Performance Measures and Evaluation Criteria. Trans. ASABE 2015, 58, 1763–1785. [Google Scholar] [CrossRef]
- Bressiani, D.A.; Srinivasan, R.; Jones, C.A.; Mendiondo, E.M. Effects of spatial and temporal weather data resolutions on streamflow modeling of a semi-arid basin, Northeast Brazil. Int. J. Agric. Biol. Eng. 2015, 8, 125–139. [Google Scholar]
- Ritter, A.; Muñoz-Carpena, R. Predictive ability of hydrological models: Objective assessment of goodness-of-fit with statistical significance. J. Hydrol. 2013, 480, 33–45. [Google Scholar] [CrossRef]
- Témez, J.R. Modelo Matemático de Trasformación “Precipitación-Escorrentía”; Asociación de Investigación Industrial Eléctrica (ASINEL): Madrid, Spain, 1977. [Google Scholar]
- Edijatno, N.; Michel, C. Un modèle pluie-débit journalier a trois paramètres. LHBL 1989, 2, 113–121. [Google Scholar] [CrossRef]
- Kabouya, M. Modélisation pluie-débit aux pas de temps mensuel et annuel en Algérie septentrionale. Ph.D. Thesis, Université Paris Sud Orsay, Orsay, France, 1990. [Google Scholar]
- Paturel, J.E.; Servat, E.; Vassiliadis, A. Sensitivity of conceptual rainfall-run-off algorithms to errors in input data. Case of the GR2M model. J. Hydrol. 1995, 168, 111–125. [Google Scholar] [CrossRef]
- Nief, H.; Paturel, J.E.; Servat, E. Study of parameter stability of a lumped hydrologic model in a context of climatic variability. J. Hydrol. 2003, 278, 213–230. [Google Scholar]
- Thornthwaite, C.W.; Mather, J.R. The water balance. Publ. Climatol. 1955, 8, 1–104. [Google Scholar]
- KlemeŠ, V. Operational testing of hydrological simulation models. Hydrol. Sci. J. 1986, 31, 13–24. [Google Scholar] [CrossRef]
- Fylstra, D.; Lasdon, L.; Watson, J.; Waren, A. Design and use of the Microsoft Excel Solver. Interfaces 1998, 28, 29–55. [Google Scholar] [CrossRef]
- Ríos, S. Investigación Operativa; Centro de Estudios Ramón Areces: Madrid, Spain, 1988. [Google Scholar]
- Abadie, J. The GRG Method for Nonlinear Programming. In Design and Implementation of Optimization Software; Greenberg, H.J., Ed.; Sijthoff and Noordhoof: Alphen aan den Rijn, The Netherlands, 1978. [Google Scholar]
- Lasdon, L.S.; Waren, A.D. Generalized Reduced Gradient Software for Linearly and Nonlinearly Constrained Problems. In Design and Implementation of Optimization Software; Greenberg, H.J., Ed.; Sijthoff and Noordhoof: Alphen aan den Rijn, The Netherlands, 1978. [Google Scholar]
- Lasdon, L.S.; Waren, A.D.; Jain, A.; Ratner, M. Design and Testing of a Generalized Reduced Gradient Code for Nonlinear Constrained Programming. ACM Trans. Math. Softw. 1978, 4, 34–50. [Google Scholar] [CrossRef]
- Nuno, R.C.; Lopes, Z.; Pereira, Z.; Pereira, L. Multiple response optimization: A global criterion-based method. J. Chemom. 2010, 24, 333–342. [Google Scholar] [CrossRef]
- Ravinder, H.V. Determining the Optimal Values of Exponential Smoothing Constants—Does Solver Really Work? AJBE 2013, 6, 347–360. [Google Scholar] [CrossRef]
- Nash, J.E.; Sutcliffe, J.V. River flow forecasting through conceptual models: Part 1. A discussion of principles. J. Hydrol. 1970, 10, 282–290. [Google Scholar] [CrossRef]
- Pearson, K. Notes on regression and inheritance in the case of two parents. Proc. R. Soc. Lond. 1985, 58, 240–242. [Google Scholar]
- Gupta, H.V.; Sorooshian, S.; Yapo, P.O. Status of automatic calibration for hydrologic models: Comparison with multilevel expert calibration. J. Hydrol. Eng. 1999, 4, 135–143. [Google Scholar] [CrossRef]
- Karpouzos, D.K.; Baltas, E.A.; Kavalieratou, S.; Babajimopoulos, C. A hydrological investigation using a lumped water balance model: The Aison River Basin case (Greece). Water Environ. J. 2011, 25, 297–307. [Google Scholar] [CrossRef]
- Yilmaz, K.K.; Gupta, H.V.; Wagener, T. A process-based diagnostic approach to model evaluation: Application to the NWS distributed hydrologic model. Water Resour. Res. 2008, 44, W09417. [Google Scholar] [CrossRef]
- Shafifii, M.; Tolson, B.A. Optimizing hydrological consistency by incorporating hydrological signatures into model calibration objectives. Water Resour. Res. 2015, 5, 3796–3814. [Google Scholar] [CrossRef]
- Bai, P.; Liu, X.; Liang, K.; Liu, C. Comparison of performance of twelve monthly balance models in different climatic catchments of China. J. Hydrol. 2015, 529, 1030–1040. [Google Scholar] [CrossRef]
- Clark, M.P.; Slater, A.G.; Rupp, D.E.; Woods, R.A.; Vrugt, J.A.; Gupta, H.V.; Wagener, T.; Hay, L.E. Framework for Understanding Structural Errors (FUSE): A modular framework to diagnose differences between hydrological models. Water Resour. Res. 2008, 44, W00B02. [Google Scholar] [CrossRef]
- Jakeman, A.J.; Hornberger, G.M. How much complexity is warranted in a rainfall-run-off model? Water Resour. Res. 1993, 29, 2637–2649. [Google Scholar] [CrossRef]
- Michaud, J.; Sorooshian, S. Comparison of simple versus complex distributed run-off models on a midsized semiarid watershed. Water Resour. Res. 1994, 30, 593–605. [Google Scholar] [CrossRef]
- Beven, K. Changing ideas in hydrology—The case of physically-based models. J. Hydrol. 1989, 105, 157–172. [Google Scholar] [CrossRef]
- Yew Gan, T.; Dlamini, E.M.; Biftu, G.F. Effects of model complexity and structure, data quality, and objective functions on hydrologic modeling. J. Hydrol. 1997, 192, 81–103. [Google Scholar] [CrossRef]
- Krause, P.; Boyle, D.; Bäse, F. Comparison of different efficiency criteria for hydrological model assessment. Adv. Geosci. 2005, 5, 89–97. [Google Scholar] [CrossRef]
- Legates, D.R.; McCabe, G.J. Evaluating the use of “goodness–of–fit” measures in hydrologic and hydroclimatic model validation. Water Resour. Res. 1999, 35, 233–241. [Google Scholar] [CrossRef]
- Cho, H.; Olivera, F. Effect of the spatial variability of land use, soil type, and precipitation on streamflows in small watersheds. JAWRA 2009, 45, 1423–1431. [Google Scholar] [CrossRef]
- El-Nasr, A.; Arnold, J.G.; Feyen, J.; Berlamont, J. Modelling the hydrology of a catchment using a distributed and a semi-distributed model. Hydrol. Process. 2005, 19, 573–587. [Google Scholar] [CrossRef]
- Booij, M.J. Impact of climate change on river flooding assessed with different spatial model resolutions. J. Hydrol. 2005, 303, 176–198. [Google Scholar] [CrossRef]
- Beven, K. A Manifesto for the Equifinality Thesis. J. Hydrol. 2006, 320, 18–36. [Google Scholar] [CrossRef]
- Operacz, A.; Wałega, A.; Cupak, A.; Tomaszewska, B. The comparison of environmental flow assessment—The barrier for investment in Poland or river protection? J. Clean. Prod. 2018, 193, 575–592. [Google Scholar] [CrossRef]
- Pusłowska-Tyszewska, D.; Tyszewski, S. Attempt at Implementing the 2015 “Ecological Flow Assessment Method for Poland” In the Wieprza River Catchment. Acta Sci. Pol. Form. Circumiectus 2018, 17, 181–193. [Google Scholar] [CrossRef]
- Neitsch, S.; Arnold, J.; Kiniry, J.E.A.; Srinivasan, R.; Williams, J. Soil and Water Assessment Tool User’s Manual: Version 2012. Available online: https://swat.tamu.edu/docs/ (accessed on 12 February 2019).







| Code | Name | Area (km2) | Pfafstetter Code | X ETRS89 UTM 30N | Y ETRS89 UTM 30N | MASL (m) | Köppen Class. | UNEP Aridity Index | Average Temperature (°C) | Average Yearly Precipitation (mm) | Average Yearly ETP (mm) | CLC Variation (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| AND | Andoain | 778.49 | 172988 | 573,531.02 | 4,769,234.41 | 486.01 | Cfb | 2.15 | 11.62 | 1563.47 | 727.86 | 5.23 |
| BEG | Begonte | 836.89 | 104080 | 111,096.28 | 4,799,111.26 | 504.01 | Csb | 2.07 | 11.44 | 1332.62 | 632.50 | 1.89 |
| BOL | Bolulla | 29.23 | 806014 | 749,970.13 | 4,286,756.78 | 600.31 | Csa | 0.54 | 16.56 | 579.71 | 1080.30 | 0.00 |
| COT | Coterillo | 488.22 | 184926 | 460,081.35 | 4,786,345.03 | 559.51 | Cfb | 1.65 | 11.48 | 1311.12 | 793.16 | 2.47 |
| CUE | Cuernacabras | 139.86 | 308769 | 280,997.89 | 4,392,588.21 | 610.63 | Csa | 0.52 | 15.33 | 570.56 | 1098.46 | 1.32 |
| GAR | Gargüera | 69.92 | 301389 | 251,972.85 | 4,439,204.60 | 689.98 | Csa | 1.02 | 14.73 | 1060.18 | 1043.32 | 5.31 |
| HOY | Hoyos | 66.15 | 211914 | 318,316.11 | 4,466,995.19 | 1632.12 | Csb | 1.01 | 8.58 | 777.22 | 770.35 | 0.87 |
| JUB | Jubera | 207.66 | 913685 | 549,719.20 | 4,553,001.74 | 1150.05 | Csb | 0.65 | 10.84 | 509.76 | 783.22 | 0.12 |
| LEM | Lemona | 252.58 | 172552 | 530,214.27 | 4,779,163.90 | 342.18 | Cfb | 1.96 | 12.35 | 1393.18 | 709.20 | 19.12 |
| PRI | Priego | 328.16 | 309656 | 578,643.32 | 4,473,678.12 | 1255.05 | Csb | 1.19 | 10.96 | 763.04 | 642.86 | 0.02 |
| PUE | Puenteareas | 263.85 | 104192 | 52,975.07 | 4,692,077.36 | 400.05 | Csb | 2.20 | 14.07 | 1662.05 | 756.42 | 5.48 |
| RVA | Vallehermoso | 85.68 | 304523 | 407,367.20 | 4,444,846.50 | 607.70 | Bsk | 0.40 | 14.69 | 396.53 | 998.49 | 9.18 |
| SEG | Segura | 232.89 | 702180 | 533,459.57 | 4,225,568.22 | 1416.46 | Csb | 0.88 | 11.53 | 807.66 | 915.83 | 0.94 |
| TAM | Tamuja | 458.12 | 309755 | 237,068.72 | 4360580.97 | 447.46 | Csa | 0.54 | 15.93 | 596.36 | 1112.84 | 0.02 |
| TRE | Trevias | 413.54 | 185314 | 217,492.08 | 4,812,225.19 | 526.64 | Cfb | 1.84 | 12.31 | 1220.91 | 663.77 | 5.00 |
| ZUM | Zumeta | 266.03 | 702184 | 536,758.71 | 4,213,732.23 | 1549.95 | Csb | 0.79 | 11.35 | 750.28 | 951.88 | 0.04 |
| Goodness-of-Fit | NSE | PBIAS (%) | R2 | Grading | Classification-Sum |
|---|---|---|---|---|---|
| Very Good (V) | 0.75 < NSE ≤ 1.00 | PBIAS < ±10 | R2 ≥ 0.85 | 3 | 7 < E ≤ 9 |
| Good (G) | 0.65 < NSE ≤ 0.75 | ±10 ≤ PBIAS < ±15 | 0.75 < R2 ≤ 0.85 | 2 | 5 < E ≤ 7 |
| Satisfactory (S) | 0.50 < NSE ≤ 0.65 | ± 5 ≤ PBIAS < ±25 | 0.60 < R2 ≤ 0.75 | 1 | 3 < E ≤ 4 |
| Unsatisfactory (U) | NSE ≤ 0.50 | PBIAS ≥ ±25 | R2 < 0.60 | Unsatisfactory | Unsatisfactory |
| Model | Number of Storages | Number of Optimized Parameters | Parameters Value Range | Optimal Value Range |
|---|---|---|---|---|
| Témez | 2 | 4 | 50 < H < 250 | 50 < H < 140 |
| 0.2 < C < 1 | 0.2 < C < 1 | |||
| 10 < I < 150 | 13 < I < 150 | |||
| 0.001 < α < 0.9 | 0.2 < α < 0.9 | |||
| ABCD | 2 | 4 | 0 < a < 1 | a = 1 |
| 5 < b | 157 < b < 554 | |||
| 0 < c < 1 | 0.35 < c < 0.83 | |||
| 0 < d < 1 | 0.015 < d < 1 | |||
| GR2M-GR4 | 2 | 4 | 0.6 < X1 < 1.9 | 0.46 < X1 < 1.87 |
| 0.03 < X2 < 18.2 | 0.07 < X2 < 0.94 | |||
| 100 < a | 126 < a < 462 | |||
| 0.2 < α < 0.5 | 0.2 < α < 0.41 | |||
| AWBM | 4 | 6 | 50 < C < 200 | 42 < C < 92 |
| 0 < B < 1 | 0.4 < B < 0.5 | |||
| 0 < K < 1 | 0.3 < K < 0.61 | |||
| 0.5 < A1 < 1.5 | 0.2 < A1 < 0.3 | |||
| 0.5 < A2 < 1.5 | 0.35 < A2 < 0.4 | |||
| 0.5 < A3 < 1.5 | 0.35 < A3 < 0.4 | |||
| Guo 5p | 2 | 5 | 0 < K0 < 2 | 0.6 < K0 < 1.5 |
| 0 < K1 < 1 | 0 < K1 < 0.5 | |||
| 0 < K2 < 1 | 0 < K2 < 0.6 | |||
| 0 < C < 1 | 0 < C < 0.7 | |||
| 0 < S | 250 < S < 1000 | |||
| Thorn Thwaite-Mather | 2 | 3 | 0 < α < 1 | 0.02 < α < 1 |
| 0 < φ | 0.001 < φ < 256 | |||
| 0 < λ < 1 | 0.001 < λ < 0.91 |
| Témez | ABCD | GR2M | AWBM | GUO5P | TH-MTH | Average | CV (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Calib. | Valid. | Calib. | Valid. | Calib. | Valid. | Calib. | Valid. | Calib. | Valid. | Calib. | Valid. | |||
| PUE | 1311 | 1268 | 1293 | 1119 | 1189 | 1058 | 1320 | 1146 | 1293 | 1135 | 1289 | 1131 | 1213 | 7.60 |
| AND | 1095 | 1213 | 1093 | 1208 | 1060 | 1182 | 1123 | 1218 | 1190 | 1148 | 1112 | 1208 | 1154 | 4.83 |
| BEG | 1150 | 1152 | 1138 | 1164 | 1114 | 1130 | 1145 | 1173 | 1139 | 1169 | 1137 | 1165 | 1148 | 1.54 |
| LEM | 1053 | 718 | 1042 | 799 | 1015 | 877 | 1064 | 786 | 1041 | 828 | 1048 | 790 | 922 | 14.41 |
| TRE | 869 | 783 | 855 | 753 | 796 | 758 | 889 | 790 | 773 | 833 | 876 | 772 | 812 | 6.06 |
| COT | 1376 | 1231 | 1286 | 1163 | 1154 | 1184 | 1389 | 1259 | 1282 | 1166 | 1278 | 1162 | 1244 | 6.60 |
| PRI | 365 | 470 | 357 | 505 | 326 | 482 | 371 | 499 | 357 | 500 | 355 | 501 | 424 | 17.24 |
| GAR | 22 | 255 | 35 | 286 | −2 | 205 | 27 | 230 | 138 | 151 | −10 | 245 | 132 | 84.95 |
| HOY | 352 | 477 | 256 | 430 | 216 | 504 | 326 | 470 | 231 | 456 | 306 | 498 | 377 | 28.72 |
| SEG | 206 | 609 | 170 | 454 | 84 | 461 | 344 | 482 | 172 | 431 | 161 | 458 | 336 | 50.37 |
| ZUM | 221 | 499 | −12 | 207 | −146 | 163 | −89 | 196 | −87 | 197 | 30 | 342 | 127 | 151.57 |
| JUB | −319 | −132 | −296 | −144 | −397 | −196 | −391 | −191 | −366 | −152 | −411 | −172 | −264 | −41.57 |
| BOL | −50 | −30 | −72 | −27 | −118 | −27 | −52 | 2 | −61 | −88 | −55 | −23 | −50 | −64.86 |
| TAM | 348 | 609 | 375 | 478 | 423 | 433 | 353 | 545 | 444 | 417 | 400 | 671 | 458 | 22.15 |
| CUE | 447 | 292 | 440 | 352 | 431 | 387 | 444 | 326 | 191 | 503 | 433 | 321 | 381 | 22.92 |
| RVA | −1050 | −316 | −1036 | −985 | −1089 | −350 | −1056 | −325 | −429 | −601 | −980 | −301 | −710 | −48.87 |
| Témez | ABCD | GR2M | AWBM | GUO5P | TH-MTH | Average | CV (%) | |||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Calib. | Valid. | Calib. | Valid. | Calib. | Valid. | Calib. | Valid. | Calib. | Valid. | Calib. | Valid. | |||
| PUE | 1324 | 1280 | 1306 | 1132 | 1213 | 1071 | 1339 | 1159 | 1309 | 1151 | 1299 | 1140 | 1227 | 7.57 |
| AND | 1108 | 1226 | 1106 | 1221 | 1083 | 1195 | 1143 | 1231 | 1206 | 1164 | 1122 | 1217 | 1168 | 4.63 |
| BEG | 1163 | 1165 | 1150 | 1177 | 1137 | 1143 | 1164 | 1186 | 1155 | 1184 | 1147 | 1174 | 1162 | 1.39 |
| LEM | 1066 | 730 | 1055 | 812 | 1038 | 890 | 1083 | 799 | 1057 | 843 | 1058 | 800 | 936 | 14.34 |
| TRE | 881 | 796 | 868 | 765 | 820 | 770 | 908 | 802 | 789 | 848 | 885 | 781 | 826 | 6.02 |
| COT | 1388 | 1243 | 1299 | 1176 | 1177 | 1197 | 1408 | 1272 | 1298 | 1182 | 1287 | 1171 | 1258 | 6.54 |
| PRI | 378 | 482 | 370 | 518 | 349 | 495 | 390 | 512 | 373 | 516 | 364 | 511 | 438 | 16.36 |
| GAR | 34 | 268 | 48 | 299 | 20 | 218 | 46 | 242 | 153 | 167 | −1 | 255 | 146 | 75.84 |
| HOY | 364 | 489 | 268 | 443 | 237 | 517 | 344 | 482 | 246 | 472 | 315 | 508 | 390 | 27.37 |
| SEG | 218 | 622 | 183 | 467 | 107 | 474 | 215 | 430 | 187 | 447 | 171 | 468 | 332 | 50.47 |
| ZUM | 233 | 511 | 1 | 220 | −123 | 176 | −70 | 209 | −71 | 213 | 40 | 352 | 141 | 134.65 |
| JUB | −306 | −120 | −283 | −131 | −374 | −196 | −372 | −178 | −350 | −136 | −401 | −163 | −251 | −42.82 |
| BOL | −38 | −17 | −59 | −27 | −95 | −15 | −33 | 15 | −46 | −72 | −45 | −14 | −37 | −78.51 |
| TAM | 360 | 621 | 388 | 490 | 423 | 445 | 372 | 557 | 460 | 432 | 410 | 680 | 470 | 21.42 |
| CUE | 460 | 304 | 452 | 365 | 454 | 400 | 463 | 338 | 207 | 519 | 443 | 331 | 395 | 22.31 |
| RVA | −1037 | −304 | −1036 | −972 | −1066 | −337 | −1037 | −312 | −413 | −585 | −970 | −292 | −697 | −49.76 |
| Catchment | Témez | ABCD | GR2M | AWBM | GUO-5P | THOR-MATH | Best Model | Classification |
|---|---|---|---|---|---|---|---|---|
| PUE | 1/1 | 2/5 | 6/5 | 1/2 | 2/4 | 2/4 | GR2M | Good |
| AND | 8/6 | 9/7 | 9/8 | 7/6 | 9/8 | 9/7 | GR2M | Very Good |
| BEG | 7/8 | 9/8 | 9/9 | 8/7 | 8/8 | 8/7 | GR2M | Very Good |
| LEM | 3/8 | 4/5 | 6/3 | 2/7 | 4/4 | 5/6 | TH-MT | Good |
| TRE | 7/8 | 8/8 | 9/8 | 5/6 | 8/7 | 6/7 | GR2M | Very Good |
| COT | 2/3 | 4/6 | 8/5 | 1/2 | 6/6 | 6/7 | TH-MT | Good |
| PRI | 6/7 | 6/7 | 8/8 | 6/7 | 6/7 | 6/6 | GR2M | Very Good |
| GAR | 8/5 | 6/4 | 9/5 | 8/5 | 7/4 | 8/5 | GR2M | Good |
| HOY | 1/0 | 4/2 | 6/0 | 1/0 | 4/1 | 1/4 | ABCD | Unsatisfactory |
| SEG | 8/3 | 8/3 | 9/3 | 8/5 | 8/4 | 9/6 | TH-MT | Good |
| ZUM | 4/0 | 6/3 | 8/6 | 8/5 | 8/5 | 4/4 | GR2M | Good |
| JUB | 5/1 | 5/3 | 8/4 | 8/3 | 6/3 | 8/5 | TH-MT | Good |
| BOL | 2/3 | 3/4 | 6/1 | 2/1 | 5/4 | 2/2 | GUO-5P | Satisfactory |
| TAM | 7/2 | 5/4 | 1/5 | 6/2 | 6/4 | 3/2 | GUO-5P | Satisfactory |
| CUE | 1/4 | 2/3 | 2/3 | 0/4 | 4/3 | 1/4 | GUO-5P | Satisfactory |
| RVA | 3/0 | 0/1 | 4/1 | 2/1 | 1/3 | 0/0 | GR2M | Unsatisfactory |
| Best Fit (Number of Times) | 0 | 1 | 8 | 0 | 4 | 4 |
| Catchment | Témez | ABCD | GR2M | AWBM | GUO-5P | THOR-MATH |
|---|---|---|---|---|---|---|
| PUE | −36.72 | −12.76 | 11.92 | −39.73 | −9.86 | −9.56 |
| AND | −12.40 | −6.44 | 3.14 | −11.45 | −0.15 | −9.85 |
| BEG | −9.53 | −5.56 | 1.72 | −11.25 | −2.83 | −10.45 |
| LEM | −9.10 | 1.04 | 14.85 | −17.41 | 1.85 | 7.11 |
| TRE | −7.41 | −0.67 | 7.38 | −14.28 | −2.23 | −9.94 |
| COT | −42.95 | −9.74 | 10.60 | −46.93 | −5.43 | −5.36 |
| PRI | −7.94 | 1.63 | 2.99 | −5.53 | −0.61 | −3.10 |
| GAR | 41.31 | 50.72 | 13.54 | 32.88 | −11.47 | 40.90 |
| HOY | −51.91 | 8.98 | 26.48 | −41.58 | 13.96 | 3.08 |
| SEG | −2.45 | 11.07 | 7.47 | 1.10 | 4.65 | 3.34 |
| ZUM | 15.43 | 11.43 | 0.41 | −2.51 | −2.08 | −1.63 |
| JUB | −15.12 | −11.59 | −8.72 | −10.54 | −13.31 | −12.31 |
| BOL | −3.30 | 10.26 | 49.61 | −4.03 | 17.32 | −1.75 |
| TAM | 89.01 | 55.40 | 58.10 | 71.97 | 13.16 | 111.98 |
| CUE | 5.15 | 20.24 | 24.40 | −3.28 | −46.18 | 12.45 |
| RVA | −63.14 | −29.66 | −47.55 | −60.21 | −33.07 | −68.22 |
| Average (Absolute Value) | 25.80 | 15.45 | 19.12 | 23.42 | 11.14 | 19.44 |
| Best fit (Number of Times) | 0 | 3 | 3 | 2 | 4 | 4 |
| Catchment | Area (km2) | Altitude (MASL) | Model | AIC | BIC | Grading Method | REV (%) |
|---|---|---|---|---|---|---|---|
| PUE | 263.85 | 400.05 | GR2M | 1 | 1 | Good | +11.92 |
| AND | 778.49 | 486.01 | GR2M | 1 | 1 | Very Good | +3.14 |
| BEG | 836.89 | 504.01 | GR2M | 1 | 1 | Very Good | +1.72 |
| LEM | 252.58 | 342.18 | Témez | 1 | 1 | Good | −9.10 |
| TRE | 413.54 | 526.64 | GR2M | 1 | 1 | Very Good | +7.38 |
| COT | 488.22 | 559.51 | Th-Mt | 2 | 1 | Good | −5.36 |
| PRI | 328.16 | 1255.05 | GR2M | 1 | 2 | Very Good | +2.99 |
| GAR | 69.92 | 689.98 | GR2M | 1 | 1 | Good | +13.54 |
| HOY | 66.15 | 1632.12 | ABCD | 1 | 1 | Unsatisfactory | +8.98 |
| SEG | 232.89 | 1416.46 | Th-Mt | 2 | 3 | Good | +3.34 |
| ZUM | 266.03 | 1549.95 | GR2M | 1 | 1 | Good | +0.41 |
| JUB | 207.66 | 1150.05 | GR2M | 1 | 1 | Good | −8.72 |
| BOL | 29.23 | 600.31 | Guo-5p | 1 | 1 | Satisfactory | +17.32 |
| TAM | 458.12 | 447.46 | Guo-5p | 1 | 2 | Satisfactory | +13.16 |
| CUE | 139.86 | 610.63 | Témez | 1 | 1 | Unsatisfactory | +5.15 |
| RVA | 85.68 | 607.70 | Guo-5p | 1 | 2 | Unsatisfactory | +11.14 |
| Catchment | Model | Probability NSE = 0.75–1.00 | Probability NSE = 0.65–0.75 | Probability NSE = 0.50–0.65 | Probability NSE < 0.50 | Classification |
|---|---|---|---|---|---|---|
| PUE | GR2M | 44.5 % | 55.1% | 0.4% | 0.0% | Good-Very Good |
| AND | GR2M | 100% | 0.0% | 0.0% | 0.0% | Very Good |
| BEG | GR2M | 100% | 0.0% | 0.0% | 0.0% | Very Good |
| LEM | Témez | 3.6% | 65.9% | 30.5% | 0.0% | Acceptable-Good |
| TRE | GR2M | 95.2% | 4.8% | 0.0% | 0.0% | Good-Very Good |
| COT | Th-Mt | 0.1% | 87.0% | 12.9% | 0.0% | Acceptable-Good |
| PRI | GR2M | 91.8% | 8.2% | 0.0% | 0.0% | Good-Very Good |
| GAR | GR2M | 94.6% | 5.2% | 0.2% | 0.0% | Good-Very Good |
| HOY | ABCD | 0.0% | 0.4% | 49.8% | 49.8% | Unsatisfactory-Acceptable |
| SEG | Th-Mt | 25.3% | 25.4% | 31.0% | 18.3% | Unsatisfactory-Very Good |
| ZUM | GR2M | 14.6% | 43.7% | 41.7% | 0.0% | Acceptable-Very Good |
| JUB | GR2M | 17.9% | 60.9% | 21.0% | 0.2% | Acceptable-Very Good |
| BOL | Guo-5p | 1.9% | 42.8% | 50.1% | 5.2% | Unsatisfactory-Good |
| TAM | Guo-5p | 34.3% | 50.0% | 15.2% | 0.5% | Acceptable-Very Good |
| CUE | Témez | 0.3% | 10.1% | 60.2% | 29.4% | Unsatisfactory-Good |
| RVA | Guo-5p | 0.2% | 5.0% | 29.5% | 65.3% | Unsatisfactory-Good |
| Catchment | Model | Observed | Simulated | Di | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| MS | HV | LV | MS | HV | LV | MS | HV | LV | ||
| PUE | GR2M | 0.71 | 1878.65 | 67.54 | 0.81 | 1435.18 | 86.01 | −14.68 | 23.61 | −27.35 |
| AND | GR2M | 0.75 | 2239.05 | 164.43 | 0.71 | 1679.94 | 122.85 | 6.0 | 25.0 | 25.3 |
| BEG | GR2M | 0.76 | 2283.95 | 61.11 | 0.73 | 1789.04 | 59.91 | 4.0 | 21.7 | 2.0 |
| LEM | Témez | 0.70 | 943.00 | 138.90 | 0.76 | 569.64 | 56.39 | −8.6 | 39.6 | 59.4 |
| TRE | GR2M | 0.58 | 701.70 | 47.69 | 0.63 | 643.24 | 59.56 | −8.6 | 8.3 | −24.9 |
| COT | Th-Mt | 0.73 | 1725.80 | 110.60 | 0.44 | 1189.46 | 74.69 | 39.5 | 31.1 | 32.5 |
| PRI | GR2M | 0.40 | 321.01 | 29.96 | 0.38 | 216.56 | 16.61 | 7.3 | 32.5 | 44.6 |
| GAR | GR2M | 0.98 | 107.54 | 181.15 | 0.74 | 94.75 | 24.97 | 24.8 | 11.9 | 86.2 |
| HOY | ABCD | 0.70 | 147.23 | 72.38 | 0.39 | 109.93 | 16.41 | 44.8 | 25.3 | 77.3 |
| SEG | Th-Mt | 0.36 | 179.70 | 24.21 | 0.57 | 198.59 | 129.37 | −56.1 | −10.5 | −434.5 |
| ZUM | GR2M | 0.35 | 118.50 | 37.60 | 0.42 | 80.15 | 145.56 | −23.0 | 32.4 | −287.2 |
| JUB | GR2M | 0.42 | 33.88 | 27.07 | 0.31 | 24.34 | 32.34 | 25.0 | 28.2 | −19.5 |
| BOL | Guo-5p | 1.10 | 45.43 | 115.76 | 4.02 | 35.13 | 696.28 | −265.3 | 22.7 | −501.5 |
| TAM | Guo-5p | 3.34 | 283.49 | 9.26 | 0.32 | 299.61 | 0.10 | 90.4 | −5.7 | 98.9 |
| CUE | Témez | 0.79 | 168.00 | 278.79 | 0.78 | 145.80 | 99.88 | 1.17 | 13.21 | 64.17 |
| RVA | Guo-5p | 1.09 | 12.55 | 37.87 | 6.05 | 14.56 | 93.40 | −455.4 | −16.1 | −146.6 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pérez-Sánchez, J.; Senent-Aparicio, J.; Segura-Méndez, F.; Pulido-Velazquez, D.; Srinivasan, R. Evaluating Hydrological Models for Deriving Water Resources in Peninsular Spain. Sustainability 2019, 11, 2872. https://doi.org/10.3390/su11102872
Pérez-Sánchez J, Senent-Aparicio J, Segura-Méndez F, Pulido-Velazquez D, Srinivasan R. Evaluating Hydrological Models for Deriving Water Resources in Peninsular Spain. Sustainability. 2019; 11(10):2872. https://doi.org/10.3390/su11102872
Chicago/Turabian StylePérez-Sánchez, Julio, Javier Senent-Aparicio, Francisco Segura-Méndez, David Pulido-Velazquez, and Raghavan Srinivasan. 2019. "Evaluating Hydrological Models for Deriving Water Resources in Peninsular Spain" Sustainability 11, no. 10: 2872. https://doi.org/10.3390/su11102872
APA StylePérez-Sánchez, J., Senent-Aparicio, J., Segura-Méndez, F., Pulido-Velazquez, D., & Srinivasan, R. (2019). Evaluating Hydrological Models for Deriving Water Resources in Peninsular Spain. Sustainability, 11(10), 2872. https://doi.org/10.3390/su11102872