Generating Worthwhile Mathematical Tasks in Order to Sustain and Develop Mathematical Thinking

Abstract

Making use of a phenomenological stance which first and foremost values the lived experience of learners, six tasks are used to illustrate what it might mean for a mathematical task to be deemed worthy of being offered to learners. These take the form of encounters with, and opportunities to develop, pervasive mathematical themes, use of mathematical powers and experience of mathematical concepts and topics. Comments about how worthwhile mathematical tasks can evolve centre around developing the propensity, the habit of mind to extend, vary and generalise for oneself. Mathematical thinking is sustained by developing this disposition.

1. Introduction

The word worthwhile in the title begs questions such as worthwhile to whom, and to what end? Here worthwhile is taken to mean that a teacher considers it worthy of a learner’s time and attention, not simply because the topic is on the curriculum, but because consequent activity could serve to enrich and enhance learner appreciation and comprehension of the use of their natural powers and of ubiquitous mathematical themes, as well as of specific mathematical constructs, procedures or topics.

What matters most to me, certainly, is the lived experience of learners. Consequently, after stating some initial assumptions, I offer some specific tasks which seem to me to illustrate and highlight qualities of worthwhile tasks, with comments about how they were generated.

2. Some Assumptions

In order that human life becomes sustainable on this planet, it is necessary that mathematical models are developed which allow us to analyse the human impact on the environment. This has been made abundantly clear in the recent Coronavirus outbreak, where governments introduced ‘lockdowns’ which had unintended consequences on employment and health due to the intricate nature of the web of economic interdependencies. Policy makers needed to know in fine detail where in the economy to inject funds so that people did not become desperate and destitute. For this, refined mathematical modelling is essential.

In order to create and to critique effective mathematical models, it is essential to have developed the use of natural powers of sense-making in a mathematical context. This includes powers such as:

• Imagining, and Expressing what is imagined, in multiple modes (words, symbols, art, …);
• Specialising and Generalising, which includes trying particular examples, and using them to detect possible generalisations;
• Conjecturing and Convincing, which includes not believing the conjecture, and trying to convince oneself, then a friend, then a sceptic;
• Classifying and Characterising constructs by means of local and global properties;
• Stressing and Ignoring, which are actions of attention, and include discerning differences.

Alongside these natural powers, which are fundamental to mathematical thinking, there are ubiquitous mathematical themes which draw upon these powers, and amongst which are:

• Doing and Undoing, which includes seeking inverses and bypasses [1];
• Seeking and exploiting Invariance in the Midst of Change;
• Extending and Restricting meaning;
• Freedom and Constraint, as in placing increasing constraints or conditions in order to limit the number of objects satisfying the constraints; most routine exercises constrain to a single object to be found (the answer).

These have been written about in many places and in many different ways (see [2,3,4,5,6,7,8,9,10,11]) so there is no need to rehearse them in detail here, and in any case, instances of some will emerge in the examples provided shortly.

It follows that a key role for mathematical tasks is to provide opportunity for learners to develop their natural powers and their appreciation of ubiquitous mathematical themes. Gattegno [6] spoke of learners educating awareness, meaning to sensitise oneself to situations in which specific actions might be useful, and to internalise those actions so as to have them become available to be enacted. The principle pedagogic actions which assist in promoting learners to internalise actions are connected with the language of scaffolding, introduced by Wood, Bruner and Ross [12] in relation to Vygotsky’s notion of ZPD [13,14] and extended to scaffolding and fading [15]; this concept is also known by the triad directed-prompted-spontaneous [16,17,18].

Educating awareness and scaffolding and fading align with the enactive or behavioural aspects of the human psyche because they involve enacting particular actions. Equally important are affective aspects, such as developing resilience without obsession, and developing a disposition to ask questions rather than to wait for instructions. Another element of affect is trusting in periods of parking: laying aside concentrated effort in order to allow additional ideas and insights to arise unbidden, which Simone Weil identified with pure attention:

Teaching should have no aim but to prepare, by training the attention, for the possibility of a certain application of the full attention to an object.

All the other advantages of instruction are without interest.

(Simone Weil [19] p.108)

Also important are cognitive aspects, such as the richness of associations and connections with other topics and with mathematical themes and powers, together with sometimes taking a broad overview rather than always being caught up in specific details of calculations. Stimulating these moves is part of the role of the inner witness, also known as the monitor or executive, which mostly observes, but which periodically asks questions such as “why are we doing this?” or “Could there be a better way?” [4,20,21].

Since attention lies at the heart of all human action, feeling and thinking, mathematical tasks are worthwhile for students if working on a task offers the opportunity to become aware of choices not only in what to attend to, but in ways of attending. Again, much has been written about attention, so there is no need to go into detail here (see [22,23,24,25,26,27]).

In summary, mathematical tasks are worthwhile for students when they serve one or more of the following purposes:

• Encountering some new concept, procedure, method, proof method, etc.;
• Exposure to ubiquitous mathematical themes;
• Opportunity to hone and refine the mathematical use of their natural powers;
• Encountering non-routine uses of a topic in apparently unrelated situations;
• Enriching students example spaces, including images and connections with other topics [28];
• Providing appropriate challenge in order to retain commitment;
• Encouraging development of a disposition to ask questions and to develop resilience without obsession;
• Providing an opportunity to recognise aspects of their psyche such as: the way the focus and locus of attention shifts and how it can sometimes be directed intentionally; how actions can be parked as well as enacted; monitoring of progress; acceptance of lack of progress; resilience; positive disposition.

The rest of this paper consists of examples of tasks from my own experience which illustrate some of the features mentioned above. The tasks have been broken into three types depending on the overt initial context of the problem source: mathematics itself, the material world and the socio-psychological world of experience. What they all have in common is that they can all be presented as phenomena rather than as simply one-off ‘facts’. Learners begin work on the tasks by trying to identify a phenomenon (something that remains invariant under certain changes), articulate what it is and what lies behind it and then try to justify their conjectures concerning what makes it a phenomenon rather than a one-off event.

The most important point of all is that the most engaging tasks, the tasks which support and promote resilience and a positive disposition, are the tasks that learners create for themselves. This is so evident from personal experience and observation that it does not require any further justification. Bill Brookes pointed out that the appropriate question is not ‘what is a problem in mathematics?’ but ‘when is a problem?’ [29,30]. In other words, what matters is appreciating the nature of the state of ‘being in question’, of feeling that something is problematic and deserves to be comprehended and resolved, and trying to induce or promote this in others. This in turn requires investigation into the sorts of conditions in which a state of ‘being in problem’ develops most readily.

In what follows, it will become evident that it seems to me to be about learning to extend, vary and generalise tasks/situations/problems/conditions that yields both appreciation of the resolution and comprehension of its relevance. Since these are two fundamental components of understanding, they are worthwhile ends in themselves.

3. Mathematics as Context

Many tasks are based within, and come from, phenomena within mathematics itself. The first task only makes use of addition, and yet many learners find it challenging. The second also starts simply but can be extended considerably.

3.1. Some Summed Grids

The task is presented in Box 1.

Box 1. Some Summed Grids task

In the adjoining grid of numbers select five entries so that you have exactly one from each row and from each column. Add them up. Make another selection and again add them up. And another.

$\begin{array}{ccccc}3& 2& 7& 5& 1\\ 5& 4& 9& 7& 3\\ 11& 10& 15& 13& 9\\ 4& 3& 8& 6& 2\\ 8& 7& 12& 10& 6\end{array}$

3.1.1. Comment

This comment, and others to follow, are immediate comments on the task itself.

The first challenge is to interpret the conditions for choosing the five grid entries. This involves discerning details and recognising relationships between the positions of cells to be selected.

It is to be hoped that readers then ask themselves how it is possible that all such sums give the same answer. It seems that the task structure of asking for an example, and another and another can have powerful effects [28].

It is tempting, as a teacher, to include some prompt which focuses attention on the fact that all the sums are the same (an invariant) and further, to prompt learners to justify this. But it is only worth initiating this pedagogical action if learners do not yet ask themselves these sorts of questions. It can then be used in a sequence of tasks which scaffold and fade prompts to learners to find and justify some invariant, and to delineate the range of permissible change of various parameters which maintain the invariance [28].

Notice the degree of intensity of your wondering how the sum can be constant. As long as there is some intensity, your attention is most likely to shift to the grid and to gaze at it, to wait upon it for a while. Certain details start to jump out (your attention moves to them). One pedagogic device that supports this is to ask learners to “Say What You See” without being either fancy or comprehensive, but rather simply picking out details. As more and more details are identified, relationships in or between them may be recognised. Some of these may be conjectured as properties which can be perceived as instantiated in several instances, leading to the possibility of reasoning on the basis of agreed properties, providing the basis for justifying conjectured properties [25].

Once attention shifts to considering pairs of rows or pairs of columns, or two-by-two sub-squares, relationships emerge which, because they hold everywhere, come to be perceived as properties. The task then becomes sorting out which properties can be deduced from which others, so that you can see how to build your own grid (of any size).

3.1.2. Follow up Questions

What aspects of this task could be changed?

In order to construct your own grid, why might it be sensible to start by filling in the main diagonal, and then a few other cells (which ones?), finishing it off by invoking properties to complete the grid?

The size of the grid could be changed (must it be square?) and the numbers used could be varied: rational numbers, decimals and negatives could be used to give learners practice adding these sorts of numbers; adding could be changed to multiplying. The use of five as both the sum and the size of the grid was an intentional red-herring. Finding a way to convince yourself that the phenomenon does always hold is the real challenge.

Beware however, that practicing adding is a low-level task. Much more engaging and attractive is to get learners to build their own Constant Sum Grid using types of numbers with which they are not yet very confident, because not only will this generate practice tasks for others, but more importantly, it will require them to rehearse adding in order to construct their own grid. There is a fundamental difference between ‘doing someone else’s exercises’, and exploring something for yourself, during which you in fact exercise the same procedures.

The shift from recognising a relationship in or between details, to perceiving a potential property being instantiated in lots of places, is a fundamental mathematical shift that may slip by many learners in schools. Yet it is quintessentially what modern mathematics is about, namely generalising and abstracting.

What other arithmetic binary operations could be used in place of addition or multiplication?

Having encountered the initial idea of a constant-sum grid, the variations afford focus on particular mathematical actions such as adding specific types of numbers.

3.2. Hurrah for Arrays

Form a rectangular grid of numbers.

For each row of your grid, write down the maximum entry in that row, in a further column to the right.

For each column, write down the minimum entry in that column, in a further row at the bottom.

Now calculate the minimum of the maxima and the maximum of the minima, and compare these.

3.2.1. Comment

Again it could be tempting to include something along the lines of “Does changing the entries in your array make any difference to the final relationship?” or even “Does this relationship hold in every possible case?”, in order to draw attention to the phenomenon, but such intervention takes away the possibility of intrigue through coming to them for oneself, as anyone who read this far without thinking about the task for themself will probably have noticed and may now appreciate.

The main challenge seems to be in developing a notation to pin down and stabilise maxima in rows and minima in columns. One approach is to swap rows and swap columns (leaving the overall maxima and minima invariant) but arranging to have a particular entry in a particular place (say the upper-left corner) so as to make comparisons easier.

3.2.2. Extensions

What can be varied in this task and still the phenomenon holds?

In reference [4] pp. 228–229, a suggestion is made which generalises the underlying structure of an array with rows and columns. Other possibilities include replacing the maximum and minimum with other functions, such as the arithmetic and geometric means, or extending the grid infinitely to right and down, possibly, but not necessarily, using convergent sequences. This leads naturally to the mathematical constructs of sup and inf and their limits, with which many learners struggle on first encounter. Using this array context provides a setting in which to gain familiarity with the ideas without simply doing routine exercises.

Once the initial task is encountered, the richness afforded by the suggested variations leads to worthwhile tasks according to pedagogic aims, such as practice with calculating particular means, or sup and inf, or experiencing the putting together of logical reasoning.

3.3. Reflection

Pedagogic power emerges when learners begin to wonder about making changes and extensions to initial tasks, so that the task becomes ‘their problem’ rather than one imposed by authority. This is most efficiently developed by learners being in the presence of someone (teacher? text?) doing this explicitly and publicly themselves. It is the import of the slogan “being mathematical with, and in front of, learners” [25], and of “Doing for learners only what they cannot yet do for themselves” [18] p. 269.

4. Material World as Context

There are many opportunities to identify phenomena in the material world, to pose and to attempt to resolve problems concerning them. These involve discerning key details, recognising possible relationships amongst them and expressing these as possible properties.

4.1. Universal Joints

When two rotating shafts are not quite in line as in a tractor towing machinery driven by the tractor’s drive shaft, the two shafts can be connected using a universal joint. The one in pictured in Figure 1 is taken from a tractor.

What questions might be asked?

4.1.1. Comment

An obvious question, to me, is to find the speed of rotation of the output shaft in terms of the speed of rotation of the input shaft. This requires some thoughtful modelling, conjecturing of relationships until being satisfied and then convincing oneself and others.

Questions about speed lead to further questions. For example, will the Lego^® model in Figure 2 actually be able to turn (note that both ends of the two shafts engage with each other via the gears)?

The theme of ‘doing and undoing’ suggests questions about using two universal joints: does the action of one get reversed or undone by a second? In Figure 3, there are two configurations of a pair of universal joints in series. How does the output speed relate to the input speed now?

Attention may need to be paid to the relationship between the two universal joints, as shown in Figure 4.

Carefully note the relative positions of the universal joints in Figure 5.

In addition to illustrating how use of a machine can stimulate and benefit from mathematical modelling, these tasks certainly call upon imagining and expressing them as a geometric model of the relationship between rotations of the two shafts, through stressing pertinent features and ignoring others. The phenomenon to be explored is the effect of a universal joint on relative speeds of rotation, and to exploit this in considering other configurations. Doing and undoing plays a role as well in the compound configurations. Put another way, what constraints are placed on the output shaft by the presence of the universal joint, and are the parallel configurations over constrained so that the shafts will not even turn?

Here the initial observation of the fact of a universal joint and what it makes possible lead to a variety of problems based around combining two or more together and predicting the effects, illustrating one way of exploring an idea. Again, the pedagogic focus is on stimulating learners to pose these and other questions themselves, rather than posing them as part of the task.

4.1.2. Hydraulic Lifts

Two pistons are connected as shown in Figure 6, and the chamber is filled with an incompressible liquid. (two positions are shown). The pistons support masses.

What questions might be asked?

This task has been extracted and formulated after seeing some hydraulic pistons in action. So the mathematical modelling has already been done, in order to address my question. The question has then been removed in order to offer a simpler situation/phenomenon to learners.

4.1.3. Comment

How is the distance moved by one piston related to the distance moved by the other?

If a mass of m is applied to the small piston, what mass could the large piston support? (assume the pistons themselves are of equal mass, then assume they are of the same density)

What other questions might arise?

I find myself eager to know what happens when there are three (or more pistons) of different sizes and supporting different masses, and what happens when systems are connected together, as in Figure 7.

To explore these, it is necessary to have worked out how the piston movements are related, as a general principle.

Notice the urge to extend, vary and perhaps generalise, and the necessity to abstract (model with symbols and algebraic expressions) in order to express relationships as instances of general properties.

Rather than creating a collection of configurations, it will be more engaging for learners and more interesting for the teacher to attract learners to constructing their own variations. If necessary, the task can have the overt aim of each learners showing, through designing particular problems, their appreciation and comprehension of the underlying ideas and of what might make a particular problem easy or hard for other learners.

5. Social Context

The next tasks can be used to introduce the use of diagrams and functions to aide both reasoning, and the articulation or narration of that reasoning. The tasks have long histories, and are the starting points for many further mathematical developments. Although their origins lie in animal behaviour, they are soon transported into the domain of mathematics (graph theory).

5.1. Greetings

If, upon coming together, a certain group of people greet each other at most once by shaking hands, what can be said about the numbers of hands people shake?

If a couple host a party attended only by other couples, and some greeting takes place, then if one of the hosts discovers that everyone else has greeted a different number of people, what can be said about the people whom the host and the host’s partner greeted?

5.2. Pecking Order

In certain groups of people, like hens in a barnyard, in each pair, one person always dominates the other. A person p is said to k-dominate someone else q if there is a chain of length at most k starting from p and ending at q in which each person dominates the next in the chain.

For what k if any, can it be guaranteed that there must be at least one k-dominator?

In the absence of a 1-dominator, and a 1-dominated, must there be people who 2-dominate and people who are 2-dominated? Can everyone be placed around a circle so that each dominates the next person clockwise?

5.3. Who Knows Whom?

If in a certain group of people, each distinct pair of people know exactly one other person in common, then what can be said about the size of the group and the numbers of people who know each other? (knowing is taken to be reflexive)

If in a certain group of people, each pair of people know-of exactly one person in common, what can be said about the number of people a person knows-of, and the number by whom they are known (knowing-of and being known-to are taken as being unidirectional).

5.3.1. Comment

It is very likely that in any reasonably sized group of learners, someone will come up with the idea of drawing a diagram consisting of nodes (people) and edges (indicating greeting or knowing, which may be directed to indicate pecking or knowing-of), which will help in refining and articulating reasoning (see the next subsection).

Trying simple cases is likely to lead to the conclusion that where knowing is a two way relationship, there must be someone who knows everyone else.

Greetings is likely to illustrate the power of systematic specialising in order to re-generalise, and the way in which attention shifts from recognising a relationship to conjecturing and then justifying the presence of a property. It is highly likely that the construction of a function will emerge naturally, even if not specifically recognised as such.

Pecking order is likely to call upon specialising, and example construction in order to modify conjectures. Justification is likely to depend on some form of induction, whether by choosing a minimal counter-example or by reducing a case to a previous smaller case.

Who Knows Whom succumbs to the use of two mathematical ideas, one from Greetings, and one from Pecking Order, once a conjecture has been made about the structure of the knowing-relationship.

It is also very likely that someone will think of considering the set of people that someone knows, which is a development of the use of a function to recognise and denote the knowing-relationship, and this may simplify the process of articulating the reasoning. If necessary, learners can be shown how their reasoning can be simplified by using diagrams and functional notation. For a more sophisticated approach, see [31] pp. 307–309.

5.3.2. On Diagrams

Teachers often find it difficult to get learners to draw diagrams. It is almost as if learners feel that they have to know what is going on in order to draw a diagram, whereas the drawing of a diagram can actually assist with finding out what is going on in a situation. Evidence for this is the number of attempted diagrams before something satisfactory emerges.

Drawing a diagram to help articulate reasoning has much in common with traditional story-tellers who use a collection of objects to remind them of different chapters in some long narrative. The diagram reduces memory load.

For example, with Who Knows Whom, using a dot to (re)present a person p who knows a maximal number of people, and drawing edges to people they must or can be assumed to know, is likely to produce something like those developed in Figure 8.

Here, dotted edges indicate knowings that have been deduced to exist, which then become solid in the next diagram. However, once you start looking at these diagrams as an aid to reasoning, the task is transformed from finding your own justification, to interpreting the sequence and so bringing to articulation a prepared justification of the conjecture, which changes the nature and quality of engagement and commitment to checking all the details.

There are two parts to the reasoning, first, to show that p must know everyone, and second, that everyone else can be paired off with someone else whom they know. It might take several attempts to trim diagrams down to the bare essentials. Furthermore, in these diagram sequences the steps have been singled out, whereas in developing your own, the new edges and points are likely to accumulate on one diagram. Only later, for purposes of exposition like this, might the diagrams be built up step by step. These ideas lead directly to the mathematical domain of graph theory (for pecking orders, see [32,33,34]).

5.3.3. Extensions

The first diagram in Figure 9 depicts the way in which the people known to the politician p pair up.

This diagram suggests in turn configurations such as the others shown in Figure 9, as candidates for some sort of generalisation. Notice the subtle shift from doing to undoing: instead of trying to formulate a more general condition to impose which will enable a conjecture to be justified, attention shifts to characterising the solution configurations, and then trying to articulate conditions which will ensure this characterisation. What if knowing is, as in ordinary life, one-way: person a may know-of person b, but b may not know-of a. So there is knowing-of someone, and being known-to someone. What configurations are then possible?

6. Reflections

In order to develop and sustain mathematical thinking in others, it is important to develop and sustain it in yourself, to develop your mathematical being. This is the best way to develop sensitivity to the experiences of learners. One way to speak about this is through the slogan “being mathematical with and in front of learners” [25]. Being mathematical in front of learners covers a spectrum of behaviour from expounding (one of six modes of interaction: see [18,26]) through responding to learners by being explicit about the use of mathematical powers within a conjecturing atmosphere, to admitting not-knowing and taking time to find something out. Being mathematical with learners covers a spectrum of behaviour from listening-to learners explaining (another mode of interaction, and distinct from listening-for [35]) through offering the occasional prompt or interjection, to overtly and genuinely learning alongside learners. These forms of being mathematical can be seen as aspects of balancing caring for learners, for mathematics and for learning [36,37,38]. As with any aspect of the human psyche, excessive even exclusive weight on being-mathematical-with or on being-mathematical-in-front-of learners can create learned dependency. Scaffolding (initial explicit directing of attention) followed by gradual fading of those prompts may be required so that learners internalise the actions which they have been experiencing and undertaking, making them available for the future.

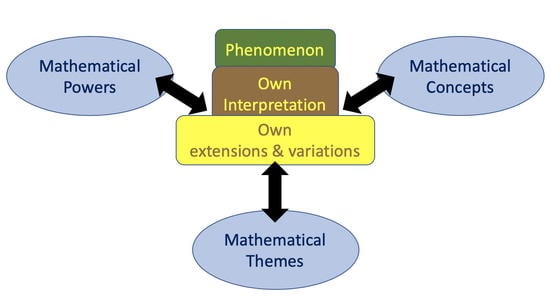
Mathematical being encompasses sensitivity to recognizing and using mathematical powers, exploiting mathematical themes, and an ever growing collection of links and associations between these and mathematical topics, concepts and procedures.

The most powerful way to get learners to engage with a task is to get them to contribute to the formulation of the problem, by identifying a phenomenon and then seeking to justify conjectures about it, by constructing their own examples with variations, extensions and generalisations, and by transforming a task by converting a ‘doing’ into an ‘undoing’.

The qualities which the presence of the teacher contribute to the mathematical development of the learners, whether in real time or via text or other media, can be summed up in the phrase the mathematical being of the teacher. What is critical is how the teacher conducts themself, what they are sensitised to be aware of, including what they are attending to and in what way and the range of pedagogical actions which are available to be enacted.

Developing and sustaining mathematical thinking is an ongoing process for everyone, as a teacher, learner, consultant or researcher. That is why it is so important to continue to practise (in both senses) your craft, your art, your attention, so as to sensitise yourself to the experience of others (learners, colleagues) and to enrich your own mathematical being through what you notice, what you attend to.