Improving Selection of Spectral Variables for Vegetation Classification of East Dongting Lake, China, Using a Gaofen-1 Image
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Sample Plot Data
2.3. Gaofen-1 Image and Transformations
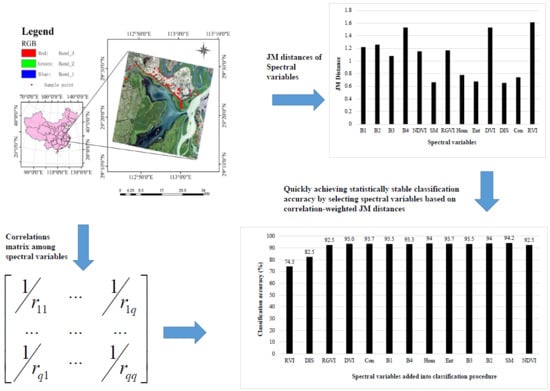
2.4. Improving Selection of Spectral Variables
- (1)
- The mean values of JM distances were utilized to rank the spectral variables for their abilities of distinguishing the land cover types. The most important spectral variable with the largest mean JM distance value was first selected to conduct the classification of the land cover types. This spectral variable was denoted with .
- (2)
- To select the second important spectral variable to be added for the classification, the correlation coefficient between each of the left q−1 spectral variables with the involved spectral variable was calculated:
- (3)
- To select the third important spectral variable to be added for the classification, the correlation coefficients of the left q − 2 spectral variables with the involved spectral variables and , were respectively calculated and their absolute inverse values of the correlation coefficients were then derived and timed with their mean JM distances. The spectral variable with the largest correlation-weighted JM distance, denoted with , was selected and added for the classification.
- (4)
- The above step 3 was repeated and , , …, were ranked and sequentially added for the classification.
3. Results
3.1. Correlations among Spectral Variables
3.2. Improving Selection of Spectral Variables for Classification
3.2.1. JM Distance and Correlation-Weighted JM Distance
3.2.2. Divergence and Correlation-Weighted Divergence
3.2.3. B-Distance and Correlation-Weighted B-Distance
3.2.4. Comparison of Methods
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Jensen, J.R. Introductory Digital Image Processing: A Remote Sensing Perspective, 4th ed.; Pearson Prentice Hall: New York, NY, USA, 2016. [Google Scholar]
- Jones, H.G.; Vaughan, R.A. Remote Sensing of Vegetation: Principles, Techniques, and Applications; Oxford University Press, Incorporated: New York, NY, USA, 2010. [Google Scholar]
- Lu, D.; Weng, Q. A survey of image classification methods and techniques for improving classification performance. Int. J. Remote Sens. 2007, 28, 823–870. [Google Scholar] [CrossRef]
- TSO, B.; Mather, P.M. Classification Methods for Remotely Sensed Data; Taylor and Francis Inc.: New York, NY, USA, 2001. [Google Scholar]
- Wang, G.; Weng, Q. Remote Sensing of Natural Resources; CRC Press, Taylor & Francis Group: Boca Raton, FL, USA, 2013. [Google Scholar]
- Haralick, R.M.; Shanmugan, K.; Dinstein, I. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, 3, 610–621. [Google Scholar] [CrossRef]
- Myint, S.W. A robust texture analysis and classification approach for urban land-use and land-cover feature discrimination. Geocarto Int. 2001, 16, 27–38. [Google Scholar] [CrossRef]
- Asner, G.P.; Heidebrecht, K.B. Spectral unmixing of vegetation, soil and dry carbon cover in arid regions: Comparing multispectral and hyperspectral observations. Int. J. Remote Sens. 2002, 23, 3939–3958. [Google Scholar] [CrossRef]
- Landgrebe, D.A. Signal Theory Methods in Multispectral Remote Sensing; John Wiley and Sons: Hoboken, NJ, USA, 2003. [Google Scholar]
- Platt, R.V.; Goetz, A.F.H. A comparison of AVIRIS and Landsat for land use classification at the urban fringe. Photogramm. Eng. Remote Sens. 2004, 70, 813–819. [Google Scholar] [CrossRef]
- Penaloza, M.A.; Welch, R.M. Feature selection for classification of Polar Regions using a fuzzy expert system. Remote Sens. Environ. 1996, 58, 81–100. [Google Scholar] [CrossRef]
- Peddle, D.R.; Ferguson, D.T. Optimisation of multisource data analysis: An example using evidential reasoning for GIS data classification. Comput. Geosci. 2002, 28, 45–52. [Google Scholar] [CrossRef]
- Lhermitte, S.; Verbesselt, J.; Verstraeten, W.W.; Coppin, P. A comparison of time series similarity measures for classification and change detection of ecosystem dynamics. Remote Sens. Environ. 2011, 115, 3129–3152. [Google Scholar] [CrossRef]
- Yan, E.; Wang, G.; Lin, H.; Xia, C.; Sun, H. Phenology-assisted classification of vegetation cover types in Northeast China with MODIS NDVI time series. Int. J. Remote Sens. 2015, 36, 489–512. [Google Scholar] [CrossRef]
- Zheng, Y.K.; Zhuang, D.F. Fourier Analysis of Multi-Temporal AVHRR Data. J. Grad. Sch. Chin. Acad. Sci. 2003, 20, 62–68. [Google Scholar]
- Swain, P.H.; Davis, S.M. Remote Sensing: The Quantitative Approach; McGraw-Hill: New York, NY, USA, 1978. [Google Scholar]
- Thomas, I.L.; Ching, N.P.; Benning, V.M.; D’Aguanno, J.A. A review of multi-channel indices of class separability. Int. J. Remote Sens. 1987, 8, 331–350. [Google Scholar] [CrossRef]
- Ferro, C.J.; Warner, T.A. Scale and texture in digital image classification. Photogramm. Eng. Remote Sens. 2002, 68, 51–63. [Google Scholar]
- Ifarraguerri, A.; Prairie, M.W. Visual Method for Spectral Band Selection. IEEE Geosci. Remote Sens. Lett. 2004, 1, 101–106. [Google Scholar] [CrossRef]
- Dalponte, M.; Bruzzone, L.; Vescovo, L.; Gianelle, D. Role of Spectral Resolution and Classifier Complexity in the Analysis of Hyperspectral Images of Forest Areas. Remote Sens. Environ. 2009, 113, 2345–2355. [Google Scholar] [CrossRef]
- Tin Kam, H. Random Decision Forests. In Proceedings of the 3rd International Conference on Document Analysis and Recognition, Montreal, QC, Canada, 14–16 August 1995; pp. 278–282. [Google Scholar]
- Tin Kam, H. The Random Subspace Method for Constructing Decision Forests. IEEE Trans. Pattern Anal. Mach. Intell. 1998, 20, 832–844. [Google Scholar] [CrossRef]
- Breiman, L. Random Forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Hao, P.; Zhan, Y.; Wang, L.; Niu, Z.; Shakir, M. Feature Selection of Time Series MODIS Data for Early Crop Classification Using Random Forest: A Case Study in Kansas, USA. Remote Sens. 2015, 7, 5347–5369. [Google Scholar] [CrossRef]
- Koreen Millard, K.; Richardson, M. On the Importance of Training Data Sample Selection in Random Forest Image Classification: A Case Study in Peatland Ecosystem Mapping. Remote Sens. 2015, 7, 8489–8515. [Google Scholar] [CrossRef]
- Wessels, K.J.; van den Bergh, F.; Roy, D.P.; Salmon, B.P.; Steenkamp, K.C.; MacAlister, B.; Swanepoel, D.; Jewitt, D. Rapid Land Cover Map Updates Using Change Detection and Robust Random Forest Classifiers. Remote Sens. 2016, 8, 888. [Google Scholar] [CrossRef]
- Sharma, R.C.; Tateishi, R.; Hara, K.; Iizuka, K. Production of the Japan 30-m Land Cover Map of 2013–2015 Using a Random Forests-Based Feature Optimization Approach. Remote Sens. 2016, 8, 429. [Google Scholar] [CrossRef]
- Deng, F.; Wang, X.; Li, E.; Cai, X.; Huang, J.; Hu, Y.; Jiang, L. Dynamics of Lake Dongting wetland from 1993 to 2010. Hupo Kexue 2012, 24, 571–576. [Google Scholar]
- Yin, G.Y.; Liu, L.M.; Jiang, X.L. The sustainable arable land use pattern under the tradeoff of agricultural production, economic development, and ecological protection—An analysis of Dongting Lake basin, China. Environ. Sci. Pollut. Res. 2017, 24, 25329–25345. [Google Scholar] [CrossRef] [PubMed]
- Singh, A.; Singh, K.K. Satellite image classification using genetic algorithm trained radial basis function neural network, application to the detection of flooded areas. J. Vis. Commun. Image Represent. 2017, 42, 173–182. [Google Scholar] [CrossRef]
- Ling, C.X.; Ju, H.B.; Zhang, H.Q.; Sun, H. Research on wetland type classification based on improved remote sensing index of worldview-2 data. For. Res. 2014, 27, 639–643. [Google Scholar]
- Hu, J.; Zhang, H.; Ling, C.; Lin, H.; Sun, H.; Wang, G. Wetland information extraction of the East Dongting Lake using mean shift segmentation. In Proceedings of the 3rd International Workshop on Earth Observation and Remote Sensing Applications (EORSA), Changsha, China, 11–14 June 2014. [Google Scholar]
- Thomas, K. The Divergence and Bhattacharyya Distance Measures in Signal Selection. IEEE Trans. Commun. Technol. 1967, 15, 52–60. [Google Scholar]
- Swain, P.H.; King, R.C. Two Effective Feature Selection Criteria for Multispectra Remote Sensing. In Proceedings of the 1st International Joint Conference on Pattern Recognition, Washington, DC, USA, 30 October–1 November 1973; pp. 536–540. [Google Scholar]
- Swain, P.H.; Roberson, T.V.; Wacker, A.G. Comparison of Divergence and B-Distance in Feature Selection; Information Note 020781; Laboratory for Application of Remote Sensing, Purdue University: West Lafayette, IN, USA, 1971. [Google Scholar]
- Mausel, P.W.; Kamber, W.J.; Lee, J.K. Optimum Band Selection for Supervised Classification of Multispectral Data. Photogramm. Eng. Remote Sens. 1990, 6, 55–60. [Google Scholar]
- Jiang, Q.X.; Townshend, J. Texture analysis method is utilized to extract the TM image information. J. Remote Sens. 2004, 5, 458–463. [Google Scholar]
- Hay, G.J.; Niemann, K.O.; Goodenough, D.G. Spatial thresholds, image-objects, and up-scaling: A multi-scale evaluation. Remote Sens. Environ. 1997, 62, 1–19. [Google Scholar] [CrossRef]
- Wang, G.; Gertner, G.Z.; Anderson, A.B. Spatial variability based algorithms for scaling up spatial data and uncertainties. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2004–2015. [Google Scholar] [CrossRef]
- Wang, G.; Gertner, G.Z.; Anderson, A.B. Up-scaling methods based on variability-weighted and simulation for inferring spatial information cross scales. Inter. J. Remote Sens. 2004, 25, 4961–4979. [Google Scholar] [CrossRef]










| B1 | B2 | B3 | B4 | NDVI | RVI | RGVI | DVI | Ent | Hom | Dis | Con | SM | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| B1 | 1 | 0.9376 | 0.9304 | 0.4281 | 0.5003 | 0.6098 | 0.4527 | 0.5768 | 0.1421 | 0.0672 | 0.0942 | 0.0268 | 0.1408 |
| B2 | 1 | 0.9318 | 0.1851 | 0.3366 | 0.4087 | 0.3280 | 0.3497 | 0.1762 | 0.1131 | 0.1538 | 0.0907 | 0.1560 | |
| B3 | 1 | 0.2481 | 0.3091 | 0.4767 | 0.6400 | 0.4215 | 0.1166 | 0.0470 | 0.1098 | 0.0594 | 0.0947 | ||
| B4 | 1 | 0.8145 | 0.9537 | 0.2909 | 0.9831 | 0.0802 | 0.0480 | 0.0411 | 0.0926 | 0.1414 | |||
| NDVI | 1 | 0.7828 | 0.1368 | 0.8210 | 0.3296 | 0.3258 | 0.2318 | 0.1511 | 0.3577 | ||||
| RVI | 1 | 0.4275 | 0.9829 | 0.1133 | 0.0616 | 0.0017 | 0.0602 | 0.1611 | |||||
| RGVI | 1 | 0.3934 | 0.0177 | 0.0687 | 0.0111 | 0.0108 | 0.0384 | ||||||
| DVI | 1 | 0.0971 | 0.0539 | 0.0177 | 0.0754 | 0.1502 | |||||||
| Ent | 1 | 0.8716 | 0.8885 | 0.7231 | 0.9799 | ||||||||
| Hom | 1 | 0.8918 | 0.7814 | 0.8282 | |||||||||
| Dis | 1 | 0.9286 | 0.8286 | ||||||||||
| Con | 1 | 0.6360 | |||||||||||
| SM | 1 |
| N. of SV | Correlation-Weighted JM Distances | Correlation-Weighted Divergences | Correlation-Weighted B-Distances | |||||||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SV | MD | RF (nt = 100) | BD | SV | MD | RF (nt = 100) | BD | SV | MD | RF (nt = 200) | BD | |
| 1 | RVI | 72.8 | 72.2 | 74.3 | RVI | 72.8 | 72.2 | 74.3 | RGVI | 43.0 | 58.5 | 59.8 |
| 2 | DIS | 78.8 | 79.8 | 82.5 | DIS | 78.8 | 79.7 | 82.5 | DIS | 65.0 | 68.8 | 74.2 |
| 3 | RGVI | 94.7 | 88.5 | 92.5 | RGVI | 94.7 | 89.0 | 92.5 | RVI | 94.7 | 88.5 | 92.5 |
| 4 | DVI | 93.0 | 88.2 | 93.0 | Con | 88.7 | 93.2 | Hom | 95.2 | 89.8 | 94.5 | |
| 5 | Con | 88.2 | 93.7 | DVI | 87.2 | 94.7 | NDVI | 93.3 | 89.5 | 93.7 | ||
| 6 | B1 | 88.0 | 93.5 | B1 | 89.8 | 93.5 | Ent | 92.8 | 89.8 | 93.7 | ||
| 7 | B4 | 92.0 | 93.3 | B4 | 92.2 | 93.3 | SM | 92.2 | 89.3 | 94.0 | ||
| 8 | Hom | 93.3 | 94.0 | Ent | 94.0 | 93.0 | Con | 89.5 | 92.3 | |||
| 9 | Ent | 93.3 | 93.7 | Hom | 92.5 | 93.7 | B1 | 90.0 | 93.7 | |||
| 10 | B3 | 93.5 | 93.5 | B3 | 93.5 | 93.5 | B2 | 92.5 | 93.3 | |||
| 11 | B2 | 93.7 | 94.0 | B2 | 93.7 | 94.0 | B3 | 92.8 | 91.7 | |||
| 12 | SM | 94.8 | 94.2 | SM | 93.8 | 94.2 | B4 | 94.0 | 93.0 | |||
| 13 | NDVI | 93.7 | 92.5 | NDVI | 94.3 | 92.5 | DVI | 93.7 | 92.5 | |||
| Land Cover Types | Willow Area | Poplar Area | Phragmites Area | Water Area | Carex Area | B&E Area | Row Total | UA (%) |
|---|---|---|---|---|---|---|---|---|
| Original divergence | ||||||||
| Willow area | 98 | 0 | 0 | 0 | 0 | 3 | 101 | 97.0 |
| Poplar area | 0 | 100 | 0 | 0 | 2 | 0 | 102 | 98.0 |
| Phragmites area | 0 | 0 | 100 | 0 | 10 | 0 | 110 | 90.9 |
| Water area | 0 | 0 | 0 | 81 | 0 | 20 | 101 | 80.2 |
| Carex area | 0 | 0 | 0 | 0 | 64 | 1 | 65 | 98.5 |
| B&E area | 2 | 0 | 0 | 19 | 24 | 76 | 121 | 62.8 |
| Col. total | 100 | 100 | 100 | 100 | 100 | 100 | ||
| PA (%) | 98 | 100 | 100 | 81 | 64 | 76 | ||
| Overall percentage correct: 86.5%, K = 0.838 | ||||||||
| Correlation-weighted divergence | ||||||||
| Willow area | 98 | 1 | 0 | 1 | 1 | 7 | 108 | 90.7 |
| Poplar area | 0 | 99 | 1 | 0 | 1 | 0 | 101 | 98.0 |
| Phragmites area | 0 | 0 | 99 | 0 | 2 | 0 | 101 | 98.0 |
| Water area | 0 | 0 | 0 | 80 | 0 | 3 | 83 | 96.4 |
| Carex area | 2 | 0 | 0 | 1 | 94 | 1 | 98 | 95.9 |
| B&E area | 0 | 0 | 0 | 18 | 2 | 89 | 109 | 81.7 |
| Col. total | 100 | 100 | 100 | 100 | 100 | 100 | ||
| PA (%) | 98 | 99 | 99 | 80 | 94 | 89 | ||
| Overall percentage correct: 93.2%, K = 0.918 | ||||||||
© 2017 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Song, R.; Lin, H.; Wang, G.; Yan, E.; Ye, Z. Improving Selection of Spectral Variables for Vegetation Classification of East Dongting Lake, China, Using a Gaofen-1 Image. Remote Sens. 2018, 10, 50. https://doi.org/10.3390/rs10010050
Song R, Lin H, Wang G, Yan E, Ye Z. Improving Selection of Spectral Variables for Vegetation Classification of East Dongting Lake, China, Using a Gaofen-1 Image. Remote Sensing. 2018; 10(1):50. https://doi.org/10.3390/rs10010050
Chicago/Turabian StyleSong, Renfei, Hui Lin, Guangxing Wang, Enping Yan, and Zilin Ye. 2018. "Improving Selection of Spectral Variables for Vegetation Classification of East Dongting Lake, China, Using a Gaofen-1 Image" Remote Sensing 10, no. 1: 50. https://doi.org/10.3390/rs10010050
APA StyleSong, R., Lin, H., Wang, G., Yan, E., & Ye, Z. (2018). Improving Selection of Spectral Variables for Vegetation Classification of East Dongting Lake, China, Using a Gaofen-1 Image. Remote Sensing, 10(1), 50. https://doi.org/10.3390/rs10010050