Evaluation of the PROSAIL Model Capabilities for Future Hyperspectral Model Environments: A Review Study

Abstract

Upcoming satellite hyperspectral sensors require powerful and robust methodologies for making optimum use of the rich spectral data. This paper reviews the widely applied coupled PROSPECT and SAIL radiative transfer models (PROSAIL), regarding their suitability for the retrieval of biophysical and biochemical variables in the context of agricultural crop monitoring. Evaluation was carried out using a systematic literature review of 281 scientific publications with regard to their (i) spectral exploitation, (ii) vegetation type analyzed, (iii) variables retrieved, and (iv) choice of retrieval methods. From the analysis, current trends were derived, and problems identified and discussed. Our analysis clearly shows that the PROSAIL model is well suited for the analysis of imaging spectrometer data from future satellite missions and that the model should be integrated in appropriate software tools that are being developed in this context for agricultural applications. The review supports the decision of potential users to employ PROSAIL for their specific data analysis and provides guidelines for choosing between the diverse retrieval techniques.

1. Introduction

For the retrieval of vegetation biophysical and biochemical properties, most studies traditionally proposed empirical relationships between the variables and optical data [1,2,3]. This approach has the advantage of straightforwardness and often yields good results. However, statistical models (e.g., a simple linear regression between vegetation indices (VI) and vegetation traits), cannot be easily generalized and require field measurements parallel to remote observations for calibration and validation purposes [4]. Additionally, not all relevant spectral information for the specific target application might be exploited when using only parts of the spectral data cube for modeling. This is the case for VIs mostly only using two or three bands concurrently and thus limiting the estimation of variables that exhibit certain levels of nonlinearity with reflectance measurements, such as leaf area index (LAI) or chlorophyll content [4,5,6]. Conversely, canopy reflectance models (CRMs) offer the possibility to significantly reduce the calibration needs. By definition, CRMs generalize well and also permit the simultaneous analysis of all spectral information in an imaging spectrometer data cube.

The very first canopy reflectance models (CRM) were established many decades ago, mainly for the purpose of understanding canopy light interception and absorption, i.e., the complex interaction of solar radiation with the vegetation canopy, see [7,8,9,10]. Since remote sensing data from airborne and satellite-based platforms have become increasingly available from the late 1980s, these models have also been exploited for the derivation of biophysical surface properties (e.g., vegetation traits) in the context of vegetation monitoring, mainly in agriculture and forestry.

CRMs can be classified according to their approach and level of complexity. They are grouped into four categories [11]:

(i)

Geometrical models (e.g., [12]) describe the canopy as translucent geometric shapes. These models may be sufficient to characterize sparse canopies where multiple scattering and shading only plays a minor role.

(ii)

Turbid medium models (e.g., [13]) treat the canopy as a horizontally uniform plane-parallel layer with absorbing and scattering particles. These models are better suited for denser canopies than (i) with the precondition that the vegetation elements are small compared to canopy height.

(iii)

Hybrid models are a combination of (i) and (ii) (e.g., [14]). They are complex but versatile models and can be used to characterize canopies that are neither dense nor sparse.

(iv)

Monte-Carlo ray tracing models (e.g., [15]) describe the radiation regime in vegetated canopies most closely to reality. Obviously, these models are the most complex and computationally-intensive.

Drawbacks of the different CRMs depend on the complexity of the model itself. Compared to empirical approaches, CRMs usually require stronger computational resources to perform quickly. Moreover, expert knowledge of model parameterization and inverse schemes are inevitable to permit successful outcomes.

Comprehensive reviews of CRMs exist, e.g., [11,16]. In the current review we will focus only on a turbid medium model (category ii): the widespread PROSPECT leaf model [17] combined with the Scattering by Arbitrary Inclined Leaves (SAIL) canopy model [13,18].

The coupling of the PROSPECT and SAIL models (hereafter for simplicity: PROSAIL) was used for the first time in 1992 [19] to analyze spectral shifts in the red edge spectral region. Many other studies followed, leading Jacquemoud et al. in 2009 to publish the first review article of PROSAIL analyzing the literature from 1992 to 2007 [20]. In recent years, the design and availability of a new generation of satellite sensor data empowered more complex approaches that can fully exploit the richer information content in the spectral (e.g., from future EnMAP satellite data), spatial (e.g., from GeoEye sensors), and temporal domains (e.g., from the Copernicus mission). Due to this growing interest, the PROSAIL model requires a new evaluation in terms of accuracy and possibilities of application. This is warranted not only in scientific context but also in view of operational processing chains for current and future satellite missions. Therefore, the main objective of the present study is to provide a systematic review of the usage of PROSAIL for vegetation studies focusing on agricultural applications. A motivation behind this work is the evaluation of the model in view of its final implementation into the software EnMAP-Box [21], designed to support the use of data from the German Spaceborne Imaging Spectrometer Mission EnMAP [22] in the context of biophysical and biochemical variable estimation. Moreover, we aim to support other potential users to apply PROSAIL for their specific purposes using both multi- and hyperspectral datasets for diverse vegetation types.

The paper is organized in the following way: Section 2 describes the model and its range of versions. In Section 3, the main PROSAIL applications are pointed out. Section 4 explains the identification of all peer-reviewed articles of interest. In the Section 5, Section 6, Section 7, Section 8 and Section 9, a statistical overview is given about the analyzed literature in terms of spectral exploitation (Section 5), vegetation type analyzed (Section 6), biophysical and biochemical variables of interest (Section 7), applied retrieval algorithms (Section 8), and geographic situations (Section 9). All these issues are disputed focusing on the performance of the model and retrievals regarding current trends and existing problems. Conclusions (Section 10) summarize the potential suitability of PROSAIL for hyperspectral data analysis, with a special focus on agricultural areas. Moreover, potential research gaps are highlighted.

2. The PROSAIL Model

2.1. Overview

PROSAIL combines the leaf optical properties model PROSPECT with the turbid medium canopy radiative transfer model SAIL. The models are coupled so that the simulated leaf reflectance and transmittance from PROSPECT are fed into the SAIL model, completed with information about soil optical properties and illumination/observation geometry (see Figure 1).

The leaf optical properties model PROSPECT is central to the success of PROSAIL as it simulates the spectral range from 400 to 2500 nm with only a limited number of parameters, describing the biophysical properties of a single leaf. PROSPECT itself is based on Allen’s generalized “plate model” [23] and received several modifications. Its first version simulated leaf reflectance and transmittance as a function of only three input parameters: the internal structure parameter of the leaf mesophyll (N), chlorophyll a + b concentration (C_ab), and leaf water content (C_w) [17]. More recent versions include additional parameters, such as dry matter content (C_m) or leaf mass per area (LMA), brown pigments (C_bp), and total carotenoid content (C_cx). More detailed descriptions of the various model versions can be found in the literature [24]. The newest version “PROSPECT-D” was published in the year 2017 [25]. In this version, besides a new calibration of specific absorption coefficients (SAC) of each pigment, leaf anthocyanin content (C_anth) was added.

The SAIL radiative transfer model is based on the 1-D model developed by Suits [26] to simulate bidirectional reflectance of a canopy [20]. PROSAIL also permits to calculate the fraction of absorbed photosynthetically active radiation (fAPAR), e.g., [27], and the fraction of vegetation cover (fCover), e.g., [28]. The SAIL model represents the canopy structure in a simple way and requires only a few parameters [29]. These include leaf reflectance and transmittance (obtained from the PROSPECT output), leaf area index (LAI), and leaf inclination distribution function (LIDF). In former PROSAIL versions, only the average leaf inclination angle (ALIA) was required. 4SAIL expects the two input parameters LIDF_a (average leaf slope) and LIDF_b (distribution bimodality) which are given for the diverse distribution functions [30]. If only the average inclination angle is known, LIDF_a is set to 0 and LIDF_b equals ALIA while angle density functions are calculated as proposed by Campbell [31]. Additionally, information about viewing geometries, i.e., sun and sensor (observer) zenith angles (SZA and OZA, respectively) as well as the relative azimuth angle between both (rAA), must be provided by the user. In 1991, the hot-spot effect was included in the model by Kuusk [32], which led to renaming into “SAILH” (not applied in the current manuscript). It requires the ratio of leaf size (width) over canopy height, introduced as the hot-spot size parameter (Hot). The fraction of diffuse incident solar radiation (skyl) is another input into the model. For more information the reader is referred to the study of Spitters et al. [33], presenting equations to estimate the share of direct and diffuse components from daily global irradiance. Moreover, a soil reflectance factor (α_soil) is used to mimic moisture-induced reflectance changes of the upper soil layer (ρ_soil), e.g., as illustrated in [27,34].

Summarizing, the current PROSAIL model calculates the canopy bidirectional reflectance from 400 to 2500 nm in 1 nm increments as a function of up to 16 input parameters, defining pigment and water content, canopy architecture, soil background, hot spot, solar diffusivity, as well as observation geometry. All parameters of the PROSPECT and SAIL model family are listed in

Table 1. Overview of the input parameters of the PROSAIL model with symbols, units and typical variable ranges published in the literature for five different crops that have been analyzed most often by the studies (see Section 6).

Parameter	Symbol	Units	Typical Ranges for Crops
			Maize [35,36,37]	Wheat [37,38]	Rice [39,40]	Soybean [41,42]	Sugar Beet [43,44,45]
Leaf Model: (PROSPECT-D)
Leaf structure index	N	Unit less	1.2–1.8	1.0–2.5	1.0–2.0	1.2–2.6	1.0–1.5
Chlorophyll a + b content	Cab	(µg/cm2)	0–80	0–80	0–80	0–80	20–45
Total carotenoid content	Ccx	(µg/cm2)	1–24	1–24	4–17	-	-
Total anthocyanin content	Canth	(µg/cm2)	-	-	-	-	-
Brown pigments	Cbp	Unit less	0–1	0–1	0–1	0–1	0–1
Dry matter content, or leaf mass per area	Cm/LMA	(g/cm2)	0.004–0.0075	0.001–0.02	0.001–0.02	0.001–0.02	0.004–0.007
Equivalent water thickness, or water depth	EWT/Cw	(cm)	0.01–0.03	0.001–0.05	0.001–0.002	0.001–0.05	0.03–0.08
Canopy Model: (4SAIL)
Leaf area index	LAI	(m2/m2)	0–7	0–8	0–10	0–7	0–4
Average leaf inclination angle * or: Leaf inclination distribution function **	ALIA LIDFa/b [30]	(°) (°)	20–70 [30]	20–90	20–80	10–75	20–40
Hot spot parameter	Hot	(m/m)	0.01–0.2	0.01–0.5	0.01–0.1	0.2	0.2–0.4
Soil reflectance	ρsoil	(%)
Soil brightness factor	αsoil	Unit less	0.5–1.5 *** or 0–1 ****
Fraction of diffuse illumination	skyl	Unit less	23% for a standard clear sky [33]
Sun zenith angle	SZA/θs	(°)	According to actual conditions during data/image acquisition
Viewing (observer) zenith angle	OZA/θv	(°)
Relative azimuth angle between sun and sensor	rAA/øSV	(°)

* characterizes an ellipsoidal leaf inclination model; ** spherical, planophile, erectophile, uniform, extremophile or plagiophile types. LIDF is characterized by LIDF_a, which controls the average leaf slope and LIDF_b which controls the distribution’s bimodality; *** to be multiplied with single ρ_soil spectrum; **** scaling factor between the two model-implemented ρ_soil spectra (wet versus dry).

, including their symbols and units. Additionally, crop-specific parameter ranges are listed for crops most often analyzed by the studies found by the systematic literature search (Figure 2): maize, wheat, rice, soybean, and sugar beet. Note that these ranges rely purely on values found in the literature and may underlie changes.

2.2. Model Variants

Originally, the SAIL model was established for the analysis of homogeneous canopies, but over the years, the model evolved to meet individual study objectives [46]. These model adaptation issues are only shortly described here as a dedicated chapter of the review paper from Jacquemoud et al. [20] discusses the model evolution in detail. For instance, to describe heterogeneous canopies with multiple layers, a multiple layer-structure was added in 2M-SAIL [47]. Decomposing vegetation canopy into stems and leaves, the SAIL model was converted into “SAIL-2” [48]. A combination of SAIL and a geometric model (iii—hybrid model) to simulate discontinuous canopies [14] was combined with PROSPECT to “GeoSAIL” [49]. The most recent variant is the numerically robust and speed-optimized hybrid two-layer version 4SAIL2. It includes improvements in the modelling of the hot spot and clumping effects as well as corrected output of canopy absorbance. Crown cover and tree shape factor are additional parameters to make the model suitable for forest analysis [50,51].

Special model versions for specific applications were also developed, such as SAILHFlood for submerged vegetation [52]. For the representation of heterogeneous canopies like forests, the ‘‘Invertible Forest Reflectance Model” (INFORM) was established [53], which is essentially a combination of the “Forest Light Interaction Model” (FLIM) [54], SAILH, and PROSPECT models.

PROSAIL was also combined with modules calculating atmospheric transfer with the REGularized canopy reFLECtance (REGFLEC) tool [55,56]. In some studies PROSAIL was coupled with the soil reflectance model SOILSPECT [57], a semi-empirical model of soil bidirectional reflectance, e.g., [58]. The soil-leaf-canopy (SLC) [50] combines a modified Hapke soil BRDF model with PROSPECT and 4SAIL2.

To analyze data outside the classical visible (VIS) to short wave infrared (SWIR) spectral region, the thermal infrared (TIR) range was included with the SAIL-Thermique model [59,60]. To take into account chlorophyll fluorescence emission (ChlF), the FluorSAIL model [61] or its newer version FluorSAIL3 [62] were published. FluorSAIL3 comprises FluorMODleaf for the calculation of leaf-level fluorescence [61] as well as a model for canopy–atmosphere coupling (MODTRAN5) [62]. The Fluspect model is another leaf ChlF-CRM also based on PROSPECT [63].

Note that specific SAIL and PROSPECT versions are embedded in the integrated radiative transfer and energy balance model “Soil-Canopy Observation of Photosynthesis and Energy” (SCOPE) [64]. Moreover, the free ARTMO (Automated Radiative Transfer Models Operator) platform provides the possibility, amongst others, to elaborate any kind of spectral data with different leaf and canopy RTMs, such as PROSPECT and SAIL [65].

In the current study, we restrict to the basic model version of the combined PROSPECT + SAIL model. In this regard, multi-layer or geometrical model versions as well as model extensions for thermal infrared or fluorescence analysis were excluded from the intense literature analysis.

3. Applications of the PROSAIL Model

PROSAIL has been used in forward mode, i.e., calculation of canopy reflectance using different input parameters, for diverse purposes (see also

Table 2. Examples of applications of the PROSAIL model in forward and inverse modes.

Applications	Exemplary References
Forward Modes:
Simulation of canopy reflectance for diverse vegetation types	[110,111]
Influence of the illumination/observation geometry on spectral reflectance (and vegetation indices)	[41,112,113]
Influence of biophysical and biochemical variables on spectral reflectance (or vegetation indices)	[37,114,115,116]
Sensitivity of canopy reflectance to leaf optical properties/Global sensitivity analysis (GSA)	[40,42,67,117,118]
Design, test and adaptation of vegetation indices	[69,119,120,121,122,123,124]
Assimilation of simulated reflectance/vegetation indices into crop growth/vegetation dynamic models	[125,126,127,128,129,130]
Emulation of canopy reflectance	[118,131,132]
Model comparisons	[79,83]
Inverse Modes:
Biophysical and biochemical variable retrieval	[5,28,39,45,133,134,135,136,137,138]
Influence of the observation geometry on variable retrieval	[38,139,140]
Determination of phenology	[44,75]
Assimilation of retrieved products into water balance models	[76,107]
Simulation and variable retrieval tests for future missions	[38,45,87,96]

in Section 4). For example, a common objective of studies using the model in forward mode was to examine the sensitivity of bi-directional canopy reflectance to different factors, for instance the effect of parameters on the red edge position (REP) of vegetation [66]. Other studies evaluated the sensitivity of canopy reflectance to leaf optical properties [67]. In this way, researchers found for example that the sensitivity of canopy reflectance to leaf reflectance is significant for large vegetation cover fractions only in spectral domains with low absorption. Also the influence of the observation geometry on red and near infrared (NIR) reflectance was investigated [68]. Other factors, such as sensitivity to canopy architecture, soil background reflectance, and atmospheric conditions were examined [69]. The PROSAIL model was also exploited for the design of new (improved) vegetation indices, e.g., [70,71].

The adoption of PROSAIL for retrieval of biophysical and biochemical variables from remotely sensed data is far more frequent than the forward modelling applications. Inversion techniques are employed when the actual input parameters of the model are the variables of interest: the actual output of the model—the remotely sensed signals or bi-directional reflectance from vegetated surfaces—then serves as input for the inverted model (see for instance Figure 7.1. in [4]). The quantification, mapping and monitoring of biophysical and biochemical vegetation properties have become increasingly important in the last years for a range of applications [72,73]. There are some specific applications, such as the correction of imaging spectroscopy data, where biophysical products are used for the evaluation of surface anisotropy corrections [74]. Other studies use RTM-derived plant traits for phenotyping [75]. Another common usage is the assimilation of simulated reflectance or remote sensing based estimates into vegetation dynamic/crop growth models (CGMs), for instance for the simulation of energy balance or plant growth [47,76].

Very systematic reviews of available algorithms for the retrieval of biophysical variables from optical remote sensing data were performed by Baret and Buis [4] and recently by Verrelst et al. [77]. The papers give comprehensive overviews of available methods and most of the inversion techniques that have been applied to the PROSAIL model. Statistical (or canopy biophysical variable-driven) approaches can be understood as parametric or non-parametric regression models adjusting the parameters for fitting reflectance values with the variable of interest [4,69,78]. In contrast to parametric regression methods, which include for instance simple ratio vegetation indices, orthogonal VIs or indices based on spectral continuum measures [69], non-parametric methods require a non-explicit choice on fitting functions and spectral band relationships. Non-parametric methods comprise linear regression methods, such as stepwise multiple linear regression (SMLR) or principal components regression (PCR), and non-linear approaches, which were also denoted as machine learning regression algorithms (MLRA). The large group of MLRAs comprises decision tree learning, artificial neural networks (ANN), kernel methods, and Bayesian networks (for details see [77]).

Physical or radiometric data-driven approaches rely on finding the best match between measured and simulated spectra [4]. Iterative numerical optimization or Markov chain Monte Carlo methods were traditionally applied for this purpose, e.g., [27,79,80,81,82,83]. Since these algorithms have known drawbacks, like high computational loads and the risk of converging to local minima [84], alternative minimization techniques such as look-up table (LUT) inversion were developed [6,36,39,85]. To this date, LUT methods may be one of the most often-used inversion strategies for the PROSAIL model. However, some of the LUT elements can be solutions of various ill-posed problems [84]. Additionally, LUT approaches still require relatively long computation time, in particular when variables must be generated for large areas or from hyperspectral data. This has contributed to the trend that many machine learning regression algorithms have been promoted in recent years [86,87], such as the kernel-based algorithm of Gaussian processes regression (GPR) [88]. The combination of the generic physical approach using a CRM with flexible, fast and effective non-parametric non-linear regression methods is considered a “hybrid approach” [77].

Over the last decade artificial neural networks have become the most popular MLRA inversion method [77]. ANNs were frequently applied to derive agronomic variables [43,89,90] and, moreover, have been the first algorithms to be implemented into operational processing chains for vegetation variable monitoring [91,92,93]. The Sentinel toolboxes, for instance, include a procedure for deriving LAI, fAPAR, fCover, C_ab and canopy water content (CWC) from Sentinel-2 data based on the ANN inversion of PROSAIL [94].

Up to now, only a few studies have tested the PROSAIL model’s suitability for data from the future German Spaceborne Imaging Spectrometer Mission EnMAP [22]. Currently under development, the dual-spectrometer instrument EnMAP will deliver data with a spectral sampling distance (SSD) of 6.5 nm in the visible to near-infrared (VNIR, 420–1000 nm) and a SSD of 10 nm in the shortwave-infrared (SWIR, 900–2450 nm) domain. Images will be acquired with a ground sampling distance of 30 m for a 30 km-wide area in the across-track direction. The expected launch date will be in 2020 (personal communication). An overview of the main characteristics of the future sensor is provided by Guanter et al. [22] and on the mission webpage [95].

Regional validation of LAI retrieval from simulated EnMAP data was promising and the authors concluded that transferable, consistent, and robust retrieval methods help to exploit the full potential of a space-borne imaging spectrometer for vegetation studies [96]. Moreover, off-nadir pointing capabilities of the future sensor can be employed to enhance the data acquisition rate [22], improving seasonal monitoring of crop development through higher temporal sampling rate. This may slightly decrease the accuracy of the variable retrievals [38] but certainly enhances the possibility to receive cloud-free scenes. Acquisitions of spatial hyperspectral data, or “Imaging Spectroscopy”, will continue to increase in the future. Besides EnMAP, other forthcoming spaceborne imaging spectroscopy missions include the Italian ASI Hyperspectral Precursor and Application Mission (PRISMA) [97], NASA HyspIRI [98], the Japanese HISUI HSI sensor for launch on ALOS-3, HYPerspectral X Imagery (HYPXIM) [99], the Spaceborne Hyperspectral Applicative Land and Ocean Mission (SHALOM) [100], or—in the long run—future ESA Sentinel-10. Suitable radiative transfer models for the analysis of these new spectral capabilities are therefore required. Many studies confirmed that the use of many contiguous spectral bands lead to more accurate variable retrievals or provides greater potential for reducing estimation uncertainties which consequently improves the accuracy and stability of the resulting biophysical and biochemical products indirectly [42,76,101,102]. Currently, a Scientific Processor for managed vegetation is under development, which will include forest and agricultural modules. This future module of the EnMAP–Box 3 software [21] will allow sophisticated variable retrieval methods from future EnMAP data, using LUTs and MLRA approaches.

4. Systematic Literature Review

A systematic literature review process was carried out as described in the scheme of Figure 2. The ISI Web of knowledge [103] was one of the main sources for the identification of relevant publications as for the review paper from Jacquemoud et al. [20]. However, instead of searching for the PROSPECT and SAIL model separately, the focus here was to look for studies using the combined model version. Therefore, the search items “PROSAIL” and “PROSPECT+SAIL” were applied in all variations for the period of 1992–2017 (see Figure 2). The second search engine used was ScienceDirect. As shown in Figure 2 in the “screening” part, duplicates from the total of 473 records were removed and those reference types identified, which were not relevant for the review study, such as conference proceedings or other non-peer reviewed works or reports. In the next step, titles and abstracts were screened in order to exclude studies from other research fields with similar naming. In the eligibility part, 334 records remained to be screened more intensely. We specifically excluded those studies fulfilling the following pre-defined criteria:

(1)

only one of both models was used (PROSPECT or SAIL);

(2)

the models were merely cited, mentioned, or planned to be used in the future;

(3)

model versions that considerably changed from the original, such as FCR [104], SAIL-2 [48], 4SAIL2 [50], SCOPE [64], or GeoSail [105].

The third exclusion criterion was added, since these more complex model versions are not planned for implementation into the EnMAP–Box 3 for the retrieval of agricultural products.

Additionally, during the paper writing process from May to November 2017, 23 more articles were published using PROSAIL (information provided through weekly Web of Science search alert, last update 16/11/2017). In the end, 281 records were left to fulfill the main criterion of having worked with the PROSAIL model in forward or inverse modes to analyze remotely sensed data for any purpose and application (see Supplementary Materials).

The most elaborative part of the study was the intense screening of the remaining articles to extract information according to the following main themes:

• study type (review/research article);
• application purpose;
• spectral exploitation: hyperspectral data acquired, used or simulated;
• vegetation type analyzed: crops, forest, grassland/shrubs, orchards, or synthetic;
• retrieved biophysical and biochemical products: leaf—and/or canopy variables;
• retrieval method: variable-driven parametric approaches (mainly simple ratio or orthogonal VIs established using PROSAIL), radiometric data-driven (iterative optimization or LUT inversion techniques) or hybrid algorithms (combining non-linear non-parametric approaches with the PROSAIL model);
• Geographic location.

Note that in the discussion and illustration of the literature review for simplicity the term “parametric” was adapted for all VI-based estimations established using the PROSAIL model. As explained in the introduction, there are several more methods categorized into parametric regressions (see [77]), which, however, have not been used in the study context.

A total number of N = 281 articles (Supplementary Materials) were screened and relevant information according to the above-mentioned criteria were extracted. Amongst those studies, eight provided reviews over specific topics, such as:

• methods to derive canopy characteristics from optical remotely sensed data [4,77];
• assimilation techniques for agroecosystem modeling [106];
• Earth Observation (E.O.) products for operational irrigation management [107];
• reviews of thirteen special issue papers that focused on novel approaches for exploiting current and future advancements in remote sensor technologies [108];
• the first PROSAIL review paper [20];
• the estimation of canopy water content from spectroscopy [109];
• the first review paper about terrestrial imaging spectroscopy and potential applications [29].

The remaining 273 records were classified as research papers using the combined PROSAIL model.

At first, a general overview of PROSAIL usages is given in Table 2. The applications are distinguished between forward and inverse modes and some exemplary references are given.

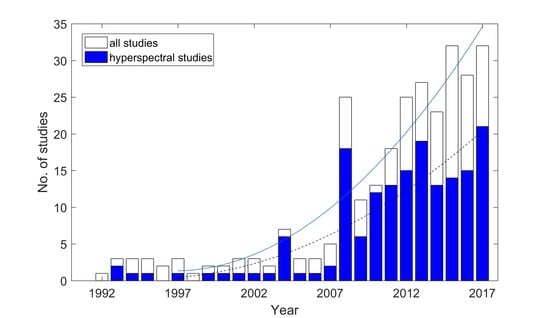
5. Annual Development and Spectral Exploitation

The histogram of Figure 3 shows the number of published PROSAIL papers from 1992 to 2017. As indicated by the solid trend line, there is an evident increase of model usage. The same holds true for studies elaborating hyperspectral data with the model, indicated by the dashed line. The year 2008 shows a significant peak for no obvious reason, even after conferring with the model authors.

The previous review study of Jacquemoud et al. [20] found a number of 29 articles published between 1992 and 2007 using PROSPECT and SAIL in the coupled version. Compared to this period, we found an almost tenfold increase up to 2017, implying the increasing importance of the model for diverse applications. Note that the absolute increase of PROSAIL model usage is in fact in accordance with the absolute increase of remote sensing and vegetation modelling studies from 1992 to 2017. Thus, there is no relative increase of works dealing with the PROSAIL model compared to all used approaches. However, the number of studies using PROSAIL is eminent compared to the application of other CRMs, such as ACRM, INFORM, GeoSAIL, or SLC models.

One reason for this may be the suitability of PROSAIL for inversions: by the combination of the canopy (SAIL) and the leaf (PROSPECT) model, a strong spectral constraint is imposed, minimizing the number of unknown variables and thus enabling the inversion procedure [20]. Nevertheless, the inversion of the model is still ill-posed, i.e., there is no unique solution, due to the fact that different combinations of parameters lead to the same spectral signal [4]. Another reason for the popularity of the model is that, unlike for vegetation indices, preliminary calibration is not needed and time-consuming and labor-intensive acquisitions of field data simultaneously to sensor-overpasses can be avoided [90,107,141]. Moreover, PROSAIL incorporates the effects of sun-target-sensor-geometry and is therefore able to simulate the specific illumination and observation conditions required. Simulated reflectance and changing parameter effects of the PROSAIL model agreed well with other 1-D models and even appeared to fit the outputs of more complex models [142]. In the year 2007, the actual versions of the SAIL model were successfully tested against other 1-D and 3-D models for homogeneous canopies in the framework of the RAdiation transfer Model Intercomparison (RAMI) experiment [143]. Overall, many studies concluded that the PROSAIL model constitutes a good compromise between the real world, model complexity, accuracy, and computation time [82,144] rendering it suitable for the analysis of hyperspectral data with multiple viewing angles.

Hyperspectral data used in the studies (blue bars in Figure 3) were mostly collected by ground-based spectrometer (ASD field spec) and airborne sensors, typically Compact Airborne Spectrographic Imager (CASI), DLR airborne sensor HySpex, Airborne imaging spectrometer HyMap or AHS, INTA. Nevertheless, the two operating hyperspectral satellite platform, i.e., ESA’s CHRIS on Proba, and Hyperion/Earth Observing-One (EO-1), were also exploited by a few studies, e.g., CHRIS [140,144,145,146] and Hyperion: [41,112,121]. The collection of hyperspectral data does not imply that the studies exploited the full spectral range measured. In contrast, most of them applied parametric regression methods using a few spectral bands (see Section 8). Overall, 45 studies were identified that specifically used hyperspectral sensor data, combined with numerical or hybrid PROSAIL inversion schemes for validation activities of agricultural biophysical and biochemical variables (mainly LAI and C_ab). Of those, a total number of N = 18 used field spectroscopy data (mainly from the FieldSpec instrument families, ASD), N = 17 used air-borne sensor data, such as HyMAP or CASI and N = 10 used satellite observation (CHRIS/Proba). Only 10% of all PROSAIL studies used data from hyperspectral satellite systems for diverse purposes, mainly biophysical and biochemical variable retrieval. This reflects the lower availability of free hyperspectral satellite data in the last decades compared to multispectral systems.

6. Vegetation Types Analyzed

As shown by the pie chart in Figure 4, tree-types were examined by 17% of the users (i.e., forests 15% and orchards 2%). Natural vegetation, which includes grassland and shrubs, was analyzed by 14% of the researches. Almost one fifth (i.e., 18%) of the studies investigated the synthetic model output for their objectives. Nearly half of the PROSAIL studies exploited a diversity of agricultural crops (49%). A distinction of crop type was only roughly performed, resulting in wheat (32%) as most often analyzed crop type, followed by maize (19%), and sugar beet (8%). Other crop types comprise rice, soybean, potato, vineyard, barley, alfalfa, cotton, mustard, sunflower, garlic, and onion.

In summary, literature analysis showed that PROSAIL was successfully used for various vegetation types, including different crops, forests, grassland, and shrubs. Vegetation with heterogeneous canopy architecture, such as orchards and forests, was thus investigated by a relatively high percentage of all studies. This is surprising, considering that there are various RTMs available which are intended for the description of discontinuous forest canopies, like INFORM [53], two- or multilayer versions of SAIL or GeoSail [14]. The basic physical assumptions of the turbid medium model PROSAIL—treating the canopy as a collection of absorbing and scattering tissues randomly distributed in a horizontal layer—rather recommends the application for homogenous crops. Indeed, a study estimating water-related variables (leaf and canopy water content) from forest, shrubs, and grassland found that the PROSAIL model inversion performance was rather limited across sites without precise in-situ knowledge [133]. For crops, most studies found that PROSAIL achieved reasonably accurate simulations, e.g., [41,83,110,111,137,147]. Compared to a three-dimensional dynamic maize model, the PROSAIL model performance was only slightly decreased [81]. Testing the model for wheat varieties, the overall shape of spectra for all combinations of view zenith and azimuth position including hotspot and dark spot positions was well simulated. The authors pointed out that the model’s performance may be suitable for deriving wheat biophysical variables from E.O. data [147]. Another work found similar trends between field-collected spectral data and PROSAIL simulated reflectance of maize and wheat canopies [78], concluding that both, the model as well as field-collected spectral measurements have the unique potential to determine crop biochemical variables, such as leaf chlorophyll content.

7. Biophysical and Biochemical Variables

The biophysical and biochemical variables that were retrieved by inverting the PROSAIL model (or deviated using PROSAIL-designed VIs) are summarized in Figure 5. The variable of strongest interest is the leaf area index (LAI). This might be due to the easier retrievability compared to other variables. Global sensitivity analysis of the PROSAIL model showed, that LAI is one of the main driving variables that influence the variations over the whole spectrum. In some spectral regions, LAI is even the dominant driver [42]. LAI is closely followed by leaf chlorophyll content (C_ab) as demonstrated by the bars in Figure 5. The combination of both—canopy chlorophyll content (CCC)—is ranked third, which is again related to the retrievability of LAI. The estimation of leaf variables, such as C_ab, from reflectance at canopy scale usually achieves lower accuracies than from leaf-scale signals. This is due to other (structural) variables, such as LAI and ALIA, strongly influencing the spectral signal on canopy level [42,145]. However, spectral measurements at leaf scale are restricted to single field-based or laboratory experiments and cannot be delivered by airborne and spaceborne sensors.

Besides retrievability, widespread and straightforward techniques for field data collection of LAI and C_ab using optical instruments may be another reason for the special interest in these variables. C_cx, fuel moisture content (FMC, a combination of C_m and C_w) and ALIA were estimated only in a few studies, albeit the latter was often highlighted as a problematic variable hindering the correct estimation of the variables of primary interest such as LAI and C_ab [27,89]. Nevertheless, the in-situ measurement of ALIA is laborious and resource-demanding, which often leads to a lack of data [148].

The retrieval accuracy for C_ab and LAI using different inversion methods was satisfying for a number of crop types that deviate more or less from the turbid medium assumption, such as cotton [145], sugar beet [136], potato [140], sunflower [149], or rice [39]. There exists, however, also critical work regarding the suitability of the model. A study investigating maize at early stage found that for row crops with incomplete coverage and strong leaf clumping, PROSAIL retrieval performance was limited [136]. This was emphasized by another study which pointed out the deficiency of PROSAIL in describing gap-driven anisotropy caused by the row structures of a (cotton) canopy. Testing the model for rice instead—a canopy type for which the turbid medium hypothesis may be more valid—PROSAIL correctly reproduced the typical bowl shaped NIR anisotropy [145]. Retrieval validation results, however, must be taken with caution, considering possible uncertainties of the ground-based variable measurements [90,136]. With the use of more complex and sophisticated models providing a more realistic canopy structure, such uncertainties might be overcome. It should be kept in mind that such complex three-dimensional models also require higher computational resources and may be partly impracticable in the frame of agricultural remote sensing applications, particularly regarding the increasing dimensionality of spectral, spatial, and temporal domains. However, recent studies have introduced the concept of emulation; i.e., the use of surrogate functions approximating the complex model structure, e.g., [132]. If this concept reaches a wider audience, more complex models could replace turbid medium approaches also within operational processing chains.

More than 85% of the analyzed studies employed the PROSAIL model for the estimation of biophysical and biochemical variables, using one or several of the discussed retrieval techniques. Leaf area index, the most frequently estimated variable from the 281 articles investigated, has an outstanding importance for plant eco-physiological processes, such as photosynthesis, evapotranspiration, interception, carbon fluxes, as well as for the detection of plant stress and diseases. Long-term global monitoring of this variable helps to identify dynamic changes in productivity and to quantify climate impacts on vegetated ecosystems. A review about LAI retrieval including other examples of applications is provided in [150]. Despite the high number of studies estimating LAI, still many problems were encountered using the PROSAIL model. One is the saturation of reflectance values occurring in particular with larger LAI values, reinforced by the complex effect of actual canopy architecture of the specific vegetation type analyzed [90]. On the other hand, at earliest and late growth stages with low LAI, the background reflectance dominates the spectral signal and thus strongly influences the variable retrieval. A solution to this problem was recently suggested [38], as two different background types were implemented in the inversion: whereas the “normal” soil reflectance characterizes the vegetative stage, a spectrum of typical non-photosynthetic vegetation was used to describe the background during the maturing stages of wheat.

The second most frequently estimated variable, C_ab, is of high interest due to its close relation to foliar chemistry parameters, in particular nitrogen, and thus its ability to indicate early plant stress [151]. The canopy scaled variable CCC is well suited for quantifying canopy level nitrogen content during early growth stages [152]. The average leaf inclination angle ALIA plays a minor role in scientific publications, as indicated by the low number of studies dealing with this variable (Figure 5). Nevertheless, just like LAI, it is a key plant canopy structure parameter affecting the radiation regime within the canopy and thus indirectly driving photosynthesis and plant productivity [153]. Therefore, more research is encouraged to investigate the retrieval of ALIA.

8. Variable Retrieval Methods

Researchers, who used the PROSAIL model for biophysical and biochemical variable retrieval, applied the following approaches:

(a)

parametric: indirect use of the model by building an arithmetic combination of two or more bands (=simple ratio or orthogonal VIs) and relating it to the variable of interest (these parametric models are then applied to real data, see also introduction);

(b)

radiometric-data driven (i): numerical iterative optimization techniques;

(c)

radiometric-data driven (ii): look-up tables (LUTs);

(d)

hybrid methods: combining a non-linear, non-parametric statistical approach with the physically based PROSAIL model. (i): ANNs and (ii): other machine learning regression algorithms, such as GPR or SVM.

Figure 6 shows the frequency of application of the discerned methods. Overall, the parametric approaches have been used the most, followed by LUTs, ANNs, iterative optimization and finally by the other MLRAs. In this context, the temporal development of application of the different methods is of special interest (Figure 7).

More than one third of all studies designed and/or tested parametric regressions, i.e., broad or narrow band vegetation indices. The application of this method to estimate the variables of interest is still a popular approach, though with decreasing tendency, as indicated by Figure 7. However, the use of VIs in so many studies is not surprising, since they are the most attractive method regarding calculation complexity and computation power and speed, while still delivering meaningful results, e.g., [69,78,124,151,154,155,156]. The reason for this decreasing trend may be attributed to an evanescence of novelty, because vegetation indices have been exhaustively designed, exploited, and adapted by the remote sensing community over decades. Their limitations, such as the lack of transferability, have been documented and confirmed by numerous studies [4,107]. Most importantly, it is widely recognized that VIs make only limited use of the full spectral resolution available, in particular with respect to hyperspectral datasets [5]. Regarding the radiometric-data driven approaches, the iterative optimization inversion techniques never reached high importance (Figure 7), due to long processing times and the risk of trapping into local “false” minima of the parameter space [84]. The LUT method instead has been extensively used in the last decade. This is on the one hand because LUTs can be parameterized to run much faster than iterative optimization techniques. Moreover, it provides the possibility to overcome the problem of local minima. A number of constraints can be implemented into the LUT parameterization to improve the estimates, such as a priori information. Weiss et al. [6] were the first to examine an LUT approach for the PROSAIL model on a synthetic data set. The study investigated the required size of an LUT and the number of selected best fits to obtain the solution. Moreover, different samplings of directional reflectance under varying observation angles were tested to estimate the biophysical and biochemical variables of interest. Note that the issue of optimal spectral sampling has been treated by many studies but goes beyond the scope of the present study [5,6,42,90,111,157,158]. The analysis of Weiss et al. has been fine-tuned by follow-up studies, investigating e.g., multiple solutions and stratification of LUTs for the retrieval of LAI and C_ab of heterogeneous grassland [134]. Moreover, a priori information was shown to improve the estimates [36,85]. Recent studies optimized the LUT structure in view of specific (future) satellite sensor missions, such as German EnMAP [22] or ESA’s Sentinel-2 and -3 families by adding noise, testing multiple best solutions, combining parameters, or applying different cost functions [38,96,159]. One study, which systematically evaluated various LUT regularization options to improve LAI and C_ab retrievals over an agricultural area, concluded that—despite the availability of a range of other suitable methods—the use of physically sound LUT-based inversion algorithms is advised for the biophysical and biochemical variable retrieval [65]. However, this study did not evaluate processing time. Considering the unprecedented hyperspectral data streams to be delivered by future missions, the LUT-based concepts will be quickly pushed to their limits. The current trend indicates that novel effective and fast MLRA techniques using PROSAIL (and other RTMs) in a hybrid manner, may overtake the LUT inversion within the next few years due to their high accuracy and transferability as proved by several studies [77,132,138], in particular for the analysis of hyperspectral data. Ideally, a combination of a dimensionality reduction (DR) method to reduce the spectral data load (in sampling or spectral domains [160]) and machine learning algorithms (e.g., GPR) combined with RTMs should be applied for the derivation of agronomic products from hyperspectral E.O. data [160]. A further advantage of these strategies is the provision of uncertainty estimates, for instance through GPR, being indispensable for variable retrievals [87]. Such hybrid retrieval designs therefore may be the core of next-generation operational retrievals [138,160].

9. Geographic Locations

High-performance computing (HPC) capabilities are now available off-the-shelf facilitating the generation, storage of, and access to large databases of RTM (PROSAIL) simulations. Multiple measurement sets of wide areas over different years and locations could then be inverted using the same database, for instance a big LUT with a large space and high diversity of canopy realizations, soil background, and illumination/viewing conditions, to characterize a wide range of vegetation properties and conditions [75]. This leads to the topic of the transferability of model results: PROSAIL has been used in an international context and for many different climate zones, vegetation types, soil characteristics, under various agricultural management conditions and with different ground, airborne, and satellite remote sensor types. To give just an insight into the variety of studies and sites with specific characteristics, the geographic locations of PROSAIL studies were as follows: several studies were carried out in large European agricultural regions, such as the Marchfeld area in Austria [161] or Lower Bavaria in Germany [38,96], characterized by temperate continental climate (Climate classification after Koeppen [162]). The Barrax site in Spain, which is situated in a cold semi-arid climate zone, was probably one of the most exploited test sites worldwide [65,76,87,90,159,163,164,165]. This was thanks to the successful ESA SPectra bARrax Campaigns (SPARC) in 2003 and 2004, generating a vast database of geo-biophysical variables simultaneously to ground based, airborne, and spaceborne remote sensing data acquisitions. In particular, SPARC represented a unique opportunity to exploit the multi-angular hyperspectral CHRIS/PROBA satellite data. Several studies chose Italian [5,82,166] or French [35,167,168] locations, characterized by warm oceanic or Mediterranean climate. Dutch [169] and English [43] test sites are influenced by temperate oceanic climate. Other test sides outside of Europe are located in south Brazil [170], Maricopa in Arizona, U.S. [75], or California, U.S. [116]. Besides the presence of agricultural regions, this distribution of test sites mainly reflects logistic issues, i.e., the possibility of collecting ground data in the frame of field campaigns. Moreover, there has been an increase in the number of Asian study sites, e.g., for Uzbekistan [145], India [171], and in particular China [151,172,173].

10. Conclusions

Considering the wide area of applications, today PROSAIL has become one of the most popular radiative transfer tools due to its outstanding features such as simplicity, robustness, and reliability in terms of consistency of validation results from lab, field-based, airborne, and satellite experiments over the last 40 years [131,174]. Moreover, the model is available for free in various computer languages and can be downloaded from a webpage [175].

The main application of the model has been the retrieval of biophysical and biochemical variables from different multi- and hyperspectral remotely sensed data (85% of all studies). Most of these studies (~80%) focused on agricultural areas, comprising crops, grassland, orchards, and synthetic vegetation. The variables of highest interest were LAI and C_ab, preferably retrieved with parametric regression methods (37%), which were established, tested or adapted using the PROSAIL model. Look-up table based model inversion schemes were applied by 25% of all retrieval studies. Except ANNs, machine learning regression algorithms, which became popular only recently, were still rarely applied (<10%). Certainly there will be a positive trend in the usage of these methods because MLRAs provide a high potential for the analyses of hyperspectral data in terms of availability, effectiveness, and speed. In view of the requirement to analyze, interpret, and retrieve agricultural products from future EnMAP and other forthcoming spaceborne imaging spectroscopy missions including HyspIRI, SHALOM, and PRISMA, future research should focus on such fast, transferable, generic, and hybrid retrieval techniques based on the PROSAIL model and suitable MLRAs, such as Gaussian processes regression [118,176]. Beside variable predictions, these models provide an assessment of uncertainty levels [176], being a pre-condition for most applications in this context. Sophisticated LUT techniques may also constitute promising estimation methods. In the context of operational processing chains in which millions of pixels—continuously streamed from new satellite sensors with improved resolution of time, space and wavelength—have to be analyzed in appropriate rates to provide users with up-to-date maps of biophysical and biochemical products; emulation should be applied to speed up the processing [118,131].

There is a clear research gap regarding the retrieval of certain biophysical and biochemical variables. With the future availability of hyperspectral data sources, the estimation of ALIA and leaf pigment variables, such as total carotenoid content or anthocyanins being key indicators of plant and crop health by influencing the nutrient, nitrogen, carbon, and water related mechanisms in plants [25], should be pushed using capable robust retrieval algorithms.

Finally, we recommend exploiting the full-spectrum data cube, as it will be available from future spaceborne spectrometers, such as EnMAP, with a full-spectrum model, such as PROSAIL, for diverse applications and retrieval purposes in the agricultural area. In this context, empirical approaches should be finally superseded by capable hybrid methods, combining the generic properties of physically based models, such as PROSAIL, with flexible and computational effective non-parametric approaches [160].

To emphasize our finding, the following points briefly list the most important recommendations of the study when hyperspectral data are to be elaborated with the PROSAIL model:

• The model’s spectral capabilities should be fully exploited instead of relying on simple empirical (parametric) models that require calibration and lack transferability.
• Machine learning regression algorithms should be further investigated in combination with dimensionality reduction methods [160], being fast and effective for hyperspectral data elaboration and providing predictions of uncertainties (in case of GPR). This is of particular interest when these data must be analyzed in near real-time in the framework of hyperspectral spaceborne missions, such as EnMAP.
• Suitable approaches to estimate plant pigments from hyperspectral data, such as carotenoids and anthocyanins, which have been implemented in the recent PROSPECT version [25], should be elaborated.

The emergence of a new generation of spaceborne spectrometers, for the first time, enables the application of the same hyperspectral instrument in all places on the globe. This will lead to comparable, i.e., identically calibrated, full-spectrum data from the most diverse and remote parts of the Earth and even will allow for the generation of hyperspectral time-series, giving access to temporal dynamics of plant physiological development. Analyzing this huge amount of most diverse data requires retrieval techniques that are both, independent from in-situ data and computationally fast. The PROSAIL model, based on our findings, seems to be ideally suited to contribute to this challenge.