Retrieval Accuracy of HCHO Vertical Column Density from Ground-Based Direct-Sun Measurement and First HCHO Column Measurement Using Pandora
Abstract
:1. Introduction
2. Methods
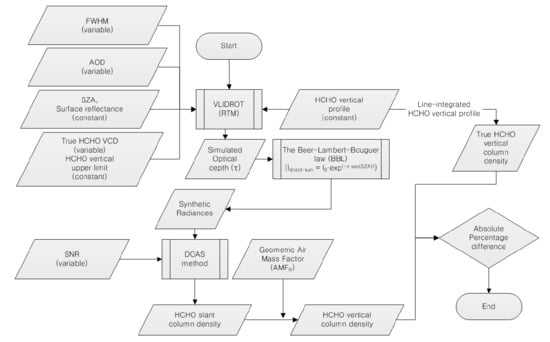
2.1. Estimation of HCHOVCD Retrieval Accuracy
2.2. Description of Pandora Measurements and Additional Datasets
2.2.1. Pandora Measurements
2.2.2. Spectral Analysis (Retrieval of HCHO Slant Column Density)
2.2.3. Ozone Monitoring Instrument (OMI) Data
3. Results
3.1. HCHO Precision Estimations
3.2. HCHOVCD Retrieval in Seoul Using Pandora
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Logan, J.A.; Prather, M.J.; Wofsy, S.C.; McElroy, M.B. Tropospheric chemistry: A global perspective. J. Geophys. Res. Oceans 1981, 86, 7210–7254. [Google Scholar] [CrossRef]
- Jiménez, R.; Martilli, A.; Balin, I.; Van den Bergh, H.; Calpini, B.; Larsen, B.; Favaro, G.; Kita, D. Measurement of Formaldehyde (HCHO) by DOAS: Intercomparison to DNPH Measurements and Interpretation from Eulerian Model Calculations. In Proceedings of the A&WMA 93rd Annual Conference, Salt Lake City, UT, USA, 18–22 June 2000. [Google Scholar]
- Hak, C.; Pundt, I.; Trick, S.; Kern, C.; Platt, U.; Dommen, J.; Ordóñez, C.; Prévôt, A.; Junkermann, W.; Astorga-Lloréns, C. Intercomparison of four different in-situ techniques for ambient formaldehyde measurements in urban air. Atmos. Chem. Phys. 2005, 5, 2881–2900. [Google Scholar] [CrossRef]
- Jones, N.; Riedel, K.; Allan, W.; Wood, S.; Palmer, P.; Chance, K.; Notholt, J. Long-term tropospheric formaldehyde concentrations deduced from ground-based fourier transform solar infrared measurements. Atmos. Chem. Phys. 2009, 9, 7131–7142. [Google Scholar] [CrossRef]
- Neitzert, V.; Seiler, W. Measurement of formaldehyde in clean air. Geophys. Res. Lett. 1981, 8, 79–82. [Google Scholar] [CrossRef]
- Tanner, R.L.; Meng, Z. Seasonal variations in ambient atmospheric levels of formaldehyde and acetaldehyde. Environ. Sci. Technol. 1984, 18, 723–726. [Google Scholar] [CrossRef]
- Harris, G.; Mackay, G.; Iguchi, T.; Mayne, L.; Schiff, H. Measurements of formaldehyde in the troposphere by tunable diode laser absorption spectroscopy. J. Atmos. Chem. 1989, 8, 119–137. [Google Scholar] [CrossRef]
- Grosjean, D.; Williams, E.L.; Seinfeld, J.H. Atmospheric oxidation of selected terpenes and related carbonyls: Gas-phase carbonyl products. Environ. Sci. Technol. 1992, 26, 1526–1533. [Google Scholar] [CrossRef]
- Arlander, D.; Cronn, D.; Farmer, J.; Menzia, F.; Westberg, H. Gaseous oxygenated hydrocarbons in the remote marine troposphere. J. Geophys. Res. Atmos. 1990, 95, 16391–16403. [Google Scholar] [CrossRef]
- Heikes, B.G. Formaldehyde and hydroperoxides at Mauna Loa observatory. J. Geophys. Res. Atmos. 1992, 97, 18001–18013. [Google Scholar] [CrossRef]
- Zhou, X.; Lee, Y.N.; Newman, L.; Chen, X.; Mopper, K. Tropospheric formaldehyde concentration at the Mauna Loa observatory during the Mauna Loa observatory photochemistry experiment 2. J. Geophys. Res. Atmos. 1996, 101, 14711–14719. [Google Scholar] [CrossRef]
- Ayers, G.; Gillett, R.; Granek, H.; De Serves, C.; Cox, R. Formaldehyde production in clean marine air. Geophys. Res. Lett. 1997, 24, 401–404. [Google Scholar] [CrossRef]
- Chance, K.V.; Palmer, P.I.; Spurr, R.J.; Martin, R.V.; Kurosu, T.P.; Jacob, D.J. Satellite observations of formaldehyde over North America from GOME. Geophys. Res. Lett. 2000. [Google Scholar] [CrossRef]
- De Smedt, I.; Müller, J.-F.; Stavrakou, T.; Van Der, A.R.; Eskes, H.; Van Roozendael, M. Twelve years of global observations of formaldehyde in the troposphere using GOME and SCIAMACHY sensors. Atmos. Chem. Phys. 2008, 8. [Google Scholar] [CrossRef]
- De Smedt, I.; Stavrakou, T.; Hendrick, F.; Danckaert, T.; Vlemmix, T.; Pinardi, G.; Theys, N.; Lerot, C.; Gielen, C.; Vigouroux, C. Diurnal, seasonal and long-term variations of global formaldehyde columns inferred from combined OMI and GOME-2 observations. Atmos. Chem. Phys. 2015, 15, 12519–12545. [Google Scholar] [CrossRef]
- Li, X.; Brauers, T.; Hofzumahaus, A.; Lu, K.; Li, Y.; Shao, M.; Wagner, T.; Wahner, A. MAX-DOAS measurements of NO2, HCHO and CHOCHO at a rural site in Southern China. Atmos. Chem. Phys. 2013, 13, 2133–2151. [Google Scholar] [CrossRef]
- Lee, H.; Ryu, J.; Irie, H.; Jang, S.-H.; Park, J.; Choi, W.; Hong, H. Investigations of the Diurnal Variation of Vertical HCHO Profiles Based on MAX-DOAS Measurements in Beijing: Comparisons with OMI Vertical Column Data. Atmosphere 2015, 6, 1816–1832. [Google Scholar] [CrossRef]
- Franco, B.; Hendrick, F.; Van Roozendael, M.; Müller, J.-F.; Stavrakou, T.; Marais, E.; Bovy, B.; Bader, W.; Fayt, C.; Hermans, C. Retrievals of formaldehyde from ground-based FTIR and MAX-DOAS observations at the Jungfraujoch station and comparisons with GEOS-Chem and IMAGES model simulations. Atmos. Meas. Tech. 2015, 8, 1733–1756. [Google Scholar] [CrossRef]
- Heckel, A.; Richter, A.; Tarsu, T.; Wittrock, F.; Hak, C.; Pundt, I.; Junkermann, W.; Burrows, J. MAX-DOAS measurements of formaldehyde in the Po-Valley. Atmos. Chem. Phys. 2005, 5, 909–918. [Google Scholar] [CrossRef]
- Vigouroux, C.; Hendrick, F.; Stavrakou, T.; Dils, B.; Smedt, I.D.; Hermans, C.; Merlaud, A.; Scolas, F.; Senten, C.; Vanhaelewyn, G. Ground-based FTIR and MAX-DOAS observations of formaldehyde at Réunion Island and comparisons with satellite and model data. Atmos. Chem. Phys. 2009, 9, 9523–9544. [Google Scholar] [CrossRef]
- Irie, H.; Takashima, H.; Kanaya, Y.; Boersma, K.; Gast, L.; Wittrock, F.; Brunner, D.; Zhou, Y.; Roozendael, M.V. Eight-component retrievals from ground-based MAX-DOAS observations. Atmos. Meas. Tech. 2011, 4, 1027–1044. [Google Scholar] [CrossRef] [Green Version]
- Peters, E.; Wittrock, F.; Großmann, K.; Frieß, U.; Richter, A.; Burrows, J. Formaldehyde and nitrogen dioxide over the remote western Pacific Ocean: SCIAMACHY and GOME-2 validation using ship-based MAX-DOAS observations. Atmos. Chem. Phys. 2012, 12, 11179–11197. [Google Scholar] [CrossRef] [Green Version]
- Pinardi, G.; Van Roozendael, M.; Abuhassan, N.; Adams, C.; Cede, A.; Clémer, K.; Fayt, C.; Frieß, U.; Gil, M.; Herman, J. MAX-DOAS formaldehyde slant column measurements during CINDI: Intercomparison and analysis improvement. Atmos. Meas. Tech. 2013, 6, 167. [Google Scholar] [CrossRef]
- Herman, J.; Cede, A.; Spinei, E.; Mount, G.; Tzortziou, M.; Abuhassan, N. NO2 column amounts from ground-based Pandora and MFDOAS spectrometers using the direct-Sun DOAS technique: Intercomparisons and application to OMI validation. J. Geophys. Res. Atmos. 2009, 114. [Google Scholar] [CrossRef]
- Herman, J.; Evans, R.; Cede, A.; Abuhassan, N.; Petropavlovskikh, I.; McConville, G. Comparison of ozone retrievals from the Pandora spectrometer system and Dobson spectrophotometer in Boulder, Colorado. Atmos. Meas. Tech. 2015, 8, 3407–3418. [Google Scholar] [CrossRef]
- Fioletov, V.E.; McLinden, C.A. Sulfur dioxide (SO2) vertical column density measurements by Pandora spectrometer over the Canadian oil sands. Atmos. Meas. Tech. 2016, 9, 2961. [Google Scholar] [CrossRef]
- Volkamer, R.; Coburn, S.; Dix, B.; Sinreich, R. MAX-DOAS observations from ground, ship, and research aircraft: Maximizing signal-to-noise to measure “weak” absorbers. In Proceeding of the SPIE Optical Engineering Applications, San Diego, CA, USA, 2–6 August 2009; Volume 7462. [Google Scholar]
- Rivera, C.; Stremme, W.; Grutter, M. Nitrogen dioxide DOAS measurements from ground and space: Comparison of zenith scattered sunlight ground-based measurements and OMI data in Central Mexico. Atmósfera 2013, 26, 401–414. [Google Scholar] [CrossRef]
- Spurr, R.; Christi, M. On the generation of atmospheric property Jacobians from the (V) LIDORT linearized radiative transfer models. J. Quant. Spectrosc. Radiat. Transf. 2014, 142, 109–115. [Google Scholar] [CrossRef]
- Wagner, T.; Beirle, S.; Brauers, T.; Deutschmann, T.; Frieß, U.; Hak, C.; Halla, J.D.; Heue, K.P.; Junkermann, W.; Li, X.; et al. Inversion of tropospheric profiles of aerosol extinction and HCHO and NO2 mixing ratios from MAX-DOAS observations in Milano during the summer of 2003 and comparison with independent data sets. Atmos. Meas. Tech. 2011, 4, 2685–2715. [Google Scholar] [CrossRef]
- Deriving Information of Surface Conditions from Column and Vertically Resolved Observations Relevant to Air Quality (Discover-AQ) Data. Available online: https://www-air.larc.nasa.gov/missions/discover-aq/discover-aq.html (accessed on 5 January 2018).
- Flynn, C.; Pickering, K.; Crawford, J.; Lamsal, L.; Krotkov, N.; Herman, J.; Weinheimer, A.; Chen, G.; Liu, X.; Szykman, J.; et al. Relationship between column-density and surface mixing ratio: Statistical analysis of O3 and NO2 data from the July 2011 Maryland DISCOVER-AQ mission. Atmos. Environ. 2014, 92, 429–441. [Google Scholar] [CrossRef]
- Jeong, U.; Kim, J.; Ahn, C.; Torres, O.; Liu, X.; Bhartia, P.K.; Spurr, R.J.; Haffner, D.; Chance, K.; Holben, B.N. An optimal-estimation-based aerosol retrieval algorithm using OMI near-UV observations. Atmos. Chem. Phys. 2016, 16, 177–193. [Google Scholar] [CrossRef]
- Hong, H.; Kim, J.; Jeong, U.; Han, K.S.; Lee, H. The Effects of Aerosol on the Retrieval Accuracy of NO2 Slant Column Density. Remote Sens. 2017, 9, 867. [Google Scholar] [CrossRef]
- Natraj, V.; Liu, X.; Kulawik, S.; Chance, K.; Chatfield, R.; Edwards, D.P.; Eldering, A.; Francis, G.; Kurosu, T.; Pickering, K. Multi-spectral sensitivity studies for the retrieval of tropospheric and lowermost tropospheric ozone from simulated clear-sky GEO-CAPE measurements. Atmos. Environ. 2011, 45, 7151–7165. [Google Scholar] [CrossRef]
- Fayt, C.; De Smedt, I.; Letocart, V.; Merlaud, A.; Pinardi, G.; Van Roozendael, M. QDOAS Software User Manual Version 1.00. 2011. Available online: http://uv-vis.aeronomie.be/software.QDOAS/index.php (accessed on 15 February 2012).
- Stutz, J.; Platt, U. Numerical analysis and estimation of the statistical error of differential optical absorption spectroscopy measurements with least-squares methods. Appl. Opt. 1996, 35, 6041–6053. [Google Scholar] [CrossRef] [PubMed]
- Platt, U.; Stutz, J. Differential absorption spectroscopy. In Differential Optical Absorption Spectroscopy; Springer: Berlin, Germany, 2008; pp. 135–174. [Google Scholar]
- Kurucz, R.L.; Furenlid, I.; Brault, J.; Testerman, L. Solar Flux Atlas from 296 to 1300 nm; National Solar Observatory Atlas, National Solar Observatory: Sunspot, NM, USA, 1984. [Google Scholar]
- Meller, R.; Moortgat, G.K. Temperature dependence of the absorption cross sections of formaldehyde between 223 and 323 K in the wavelength range 225–375 nm. J. Geophys. Res. Atmos. 2000, 105, 7089–7101. [Google Scholar] [CrossRef]
- Vandaele, A.; Hermans, C.; Simon, P.; Van Roozendael, M.; Guilmot, J.; Carleer, M.; Colin, R. Fourier transform measurement of NO2 absorption cross-section in the visible range at room temperature. J. Atmos. Chem. 1996, 25, 289–305. [Google Scholar] [CrossRef]
- Bogumil, K.; Orphal, J.; Homann, T.; Voigt, S.; Spietz, P.; Fleischmann, O.; Vogel, A.; Hartmann, M.; Kromminga, H.; Bovensmann, H. Measurements of molecular absorption spectra with the SCIAMACHY pre-flight model: Instrument characterization and reference data for atmospheric remote-sensing in the 230–2380 nm region. J. Photochem. Photobiol. A Chem. 2003, 157, 167–184. [Google Scholar] [CrossRef]
- Thalman, R.; Volkamer, R. Temperature dependent absorption cross-sections of O2–O2 collision pairs between 340 and 630 nm and at atmospherically relevant pressure. Phys. Chem. Chem. Phys. 2013, 15, 15371–15381. [Google Scholar] [CrossRef] [PubMed]
- Goddard Earth Sciences Data and Information Services Center (GES-DISC). Available online: https://disc.sci.gsfc.nasa.gov (accessed on 27 June 2017).
- Levelt, P.F.; Van den Oord, G.H.; Dobber, M.R.; Malkki, A.; Visser, H.; de Vries, J.; Stammes, P.; Lundell, J.O.; Saari, H. The ozone monitoring instrument. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1093–1101. [Google Scholar] [CrossRef]
- Chance, K. OMI algorithm theoretical basis document. In OMI Trace Gas Algorithms; Smithsonian Astrophysical Observatory: Cambridge, MA, USA, 2002; Volume 4. [Google Scholar]
- Ozone Monitoring Instrument README FILE. Available online: https://www.cfa.harvard.edu/atmosphere/Instruments/OMI/PGEReleases/READMEs/OMHCHO_README_v3.0.pdf (accessed on 27 June 2017).
- Ozone Monitoring Instrument Data User’s Guide. Available online: https://disc.gsfc.nasa.gov/Aura/data-holdings/additional/documentation/README.OMI_DUG.pdf (accessed on 27 June 2017).
- National Climate Data Service System (NCDSS). Available online: http://sts.kma.go.kr/eng/jsp/home/contents/main/main.do (accessed on 17 January 2018).
- Park, J.; Ryu, J.; Kim, D.; Yeo, J.; Lee, H. Long-Range Transport of SO2 from Continental Asia to Northeast Asia and the Northwest Pacific Ocean: Flow Rate Estimation Using OMI Data, Surface in Situ Data, and the HYSPLIT Model. Atmosphere 2016, 7, 53. [Google Scholar] [CrossRef]
- Anderson, L.G.; Lanning, J.A.; Barrell, R.; Miyagishima, J.; Jones, R.H.; Wolfe, P. Sources and sinks of formaldehyde and acetaldehyde: An analysis of Denver's ambient concentration data. Atmos. Environ. 1996, 30, 2113–2123. [Google Scholar] [CrossRef]
- Lee, C.; Kim, Y.J.; Hong, S.-B.; Lee, H.; Jung, J.; Choi, Y.-J.; Park, J.; Kim, K.-H.; Lee, J.-H.; Chun, K.-J. Measurement of atmospheric formaldehyde and monoaromatic hydrocarbons using differential optical absorption spectroscopy during winter and summer intensive periods in Seoul, Korea. Water Air Soil Pollut. 2005, 166, 181–195. [Google Scholar] [CrossRef]
- Pang, X.; Mu, Y. Seasonal and diurnal variations of carbonyl compounds in Beijing ambient air. Atmos. Environ. 2006, 40, 6313–6320. [Google Scholar] [CrossRef]
- Pang, X.; Mu, Y.; Zhang, Y.; Lee, X.; Yuan, J. Contribution of isoprene to formaldehyde and ozone formation based on its oxidation products measurement in Beijing, China. Atmos. Environ. 2009, 43, 2142–2147. [Google Scholar] [CrossRef]
- Pang, X.; Lee, X. Temporal variations of atmospheric carbonyls in urban ambient air and street canyons of a Mountainous city in Southwest China. Atmos. Environ. 2010, 44, 2098–2106. [Google Scholar] [CrossRef]
- Rappenglück, B.; Dasgupta, P.; Leuchner, M.; Li, Q.; Luke, W. Formaldehyde and its relation to CO, PAN, and SO2 in the Houston-Galveston airshed. Atmos. Chem. Phys. 2010, 10, 2413–2424. [Google Scholar] [CrossRef]









| Study | Location | Date or Campaign | Target Species | Instrument | Unit |
|---|---|---|---|---|---|
| Heckel et al. [19] | Po Valley, Northern Italy | Formaldehyde as a tracer of photo oxidation in the Troposphere (FORMAT; summer 2002) | HCHO | MAX-DOAS | Mixing ratio |
| Vigouroux et al. [20] | Réunion Island | 2004–2005 (2004–2007) | HCHO | MAX-DOAS, (FTIR) | Column density, Mixing ratio |
| Irie et al. [21] | Cabauw, the Netherlands | The Cabauw Intercomparison Campaign of Nitrogen Dioxide measuring Instruments (CINDI; summer 2009) | HCHO NO2 CHOCHO H2O SO2 O3 | MAX-DOAS | Mixing ratio |
| Peters et al. [22] | Western Pacific Ocean | TransBrom campaign (9–24 October 2009) | HCHO NO2 | MAX-DOAS | Column density |
| Pinardi et al. [23] | Cabauw, the Netherlands | The Cabauw Intercomparison Campaign of Nitrogen Dioxide measuring Instruments (CINDI; summer 2009) | HCHO | MAX-DOAS | Column density |
| Li et al. [16] | Shanghai, China | April 2010–April 2011 | HCHO NO2 | MAX-DOAS | Mixing ratio |
| De Smedt et al. [15] | Europe, China, and Africa | 2004–2014 | HCHO | MAX-DOAS, FTIR | Column density, Vertical profile |
| Lee et al. [17] | Beijing, China | Campaign of Air Quality Research in Beijing 2006 (CAREBEIJING-2006; August–September 2006) | HCHO O4 | MAX-DOAS | Column density, Vertical profile |
| Franco et al. [18] | Jungfraujoch and Monch on the northern edge of the Swiss Alps | July 2010–December 2012 | HCHO | MAX-DOAS, FTIR | Column density, Vertical profile |
| Variable | Value | Constant | Value |
|---|---|---|---|
| HCHOVCD (molecules cm−2) | Surface reflectance | 0.04 | |
| SZA | 30° | ||
| Aerosol Type | Smoke Type | ||
| AOD | 0.2, 0.6, and 1.5 | APH (km) | 0 |
| SNR | 650, 920, and 1300 | HCHO Vertical Upper Limit (km) | 2 |
| FWHM (nm) | 0.2, 0.6, and 1.0 |
| Product Name | Filter Flags and Conditions |
|---|---|
| HCHO (OMHCHOG) | Cloud fraction > 0.2 Solar zenith angle > 70° Suspect (quality flag = 1) Bad (quality flag = 2) Missing (quality flag ≤ −1) |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Park, J.; Lee, H.; Kim, J.; Herman, J.; Kim, W.; Hong, H.; Choi, W.; Yang, J.; Kim, D. Retrieval Accuracy of HCHO Vertical Column Density from Ground-Based Direct-Sun Measurement and First HCHO Column Measurement Using Pandora. Remote Sens. 2018, 10, 173. https://doi.org/10.3390/rs10020173
Park J, Lee H, Kim J, Herman J, Kim W, Hong H, Choi W, Yang J, Kim D. Retrieval Accuracy of HCHO Vertical Column Density from Ground-Based Direct-Sun Measurement and First HCHO Column Measurement Using Pandora. Remote Sensing. 2018; 10(2):173. https://doi.org/10.3390/rs10020173
Chicago/Turabian StylePark, Junsung, Hanlim Lee, Jhoon Kim, Jay Herman, Woogyung Kim, Hyunkee Hong, Wonei Choi, Jiwon Yang, and Daewon Kim. 2018. "Retrieval Accuracy of HCHO Vertical Column Density from Ground-Based Direct-Sun Measurement and First HCHO Column Measurement Using Pandora" Remote Sensing 10, no. 2: 173. https://doi.org/10.3390/rs10020173
APA StylePark, J., Lee, H., Kim, J., Herman, J., Kim, W., Hong, H., Choi, W., Yang, J., & Kim, D. (2018). Retrieval Accuracy of HCHO Vertical Column Density from Ground-Based Direct-Sun Measurement and First HCHO Column Measurement Using Pandora. Remote Sensing, 10(2), 173. https://doi.org/10.3390/rs10020173