Integration of Vessel-Based Hyperspectral Scanning and 3D-Photogrammetry for Mobile Mapping of Steep Coastal Cliffs in the Arctic
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Geological Setting
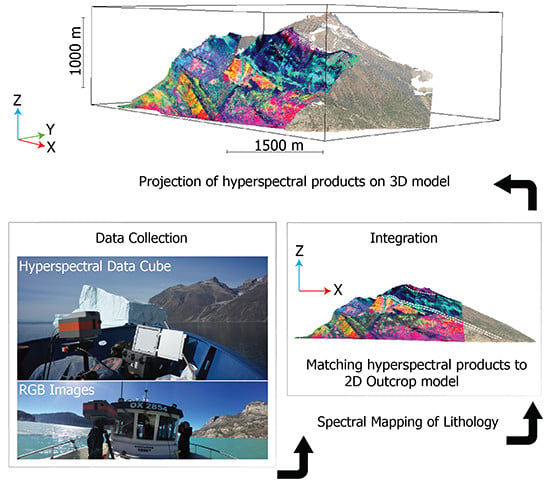
2.2. Data Acquisition
2.2.1. Instrumentation Setup
2.3. Processing Workflow
2.3.1. Pre-Processing of Hyperspectral Data
2.3.2. Geolocation of the Stereo-Images and Point Cloud Generation
2.3.3. Projection of the 3D Point Cloud onto a 2D Pseudo-Orthophoto
2.3.4. Matching the Hyperspectral Scans to the Pseudo-Orthophoto
2.4. Spectral Mapping
3. Results
3.1. Hyperspectral Classification
3.2. Integration
3.2.1. Matching Hyperspectral Products to the 2D Outcrop Model Using Transformation Matrix
3.2.2. Transformation of Hyperspectral Products into a 3D Model
3.3. Evaluation
4. Discussion
- Accurate setup of white panel within the same distance and orientation as the outcrop, essential for a realistic conversion to reflectance values, is not possible due to the inaccessibility of the observed outcrop and the fact that the platform is in motion. Consequently, the atmosphere between the vessel and vertical cliffs affects the surface reflectance spectra. Further spectral processing is needed for eliminating these effects to ensure accurate and reliable image spectra, which is crucial for the discrimination of geological targets and detailed spectral mapping applications.
- Collecting ground reflectance measurements from homogenous targets can be a solution for calculating the calibration coefficients for each band and removing the effects of atmospheric scattering and absorption to retrieve reliable data. However, when collecting reflectance spectra of the targets on the ground, sufficient measurements should be made to adequately represent any heterogeneity in the target, which due to the nature of near-vertical cliff sections is not always an option. In addition, if there is to be any time-lag between the collection of ground and vessel based data, then the spectral stability of the surface over time should be considered. Thus, it is not a feasible approach, if data are to be acquired on a large spatial scale and within a short amount of time, typical for geological surveys in the Arctic. This can alternatively be achieved by selecting an atmospheric reference spectrum from the image and correcting the image spectra based on the actual depth of atmospheric features. This approach requires additional development and could be a scope for follow-up research.
- An additional sensor-based challenge stems from the differences in the acquisition technology of frame-based RGB cameras and hyperspectral push-broom scanners rotating on a tripod. The resulting differences in viewing angle and perspective distortion can make the integration of datasets difficult. As CloudCompare (version 2.9) only supports rasterizing using orthographic view to project the point cloud onto a 2D plane, a python script was developed as part of this study to generate the perspective view for reconstructing the accurate viewing angle.
- From the mapping perspective, rocks of different chemical or mineral composition are sometimes characterized by only subtle differences in reflectance spectra [84,96,97]. However, in the context of steeply dipping cliff faces, variability in incident light also occurs causing spectral noise, which may exceed the effect of the intrinsic composition of the rocks. In such cases, it is not possible to uniquely separate and map rock units on vertical cliffs. Thus, it is essential to correct for these effects to retrieve reliable data. Moreover, surrounding topography can have a high influence on the local illumination within an image and can influence the measured at-sensor radiance by casting shadows, blocking diffuse sky irradiance or adding additional ground reflections [35]. The radiance of the same material varies, if it is located on a slope oriented toward or away from the sunlight incidence and optimal results are therefore achieved, when the view of the sensor is perpendicular to the slope of the outcrop.
- Shadows and change of scale could lead to misidentification of elevation points within the stereo model. In the present study, the experiments were performed in cloudy weather and the outcrop had a uniform steep slope without major changes in scale. The experiments as such were therefore conducted under optimal conditions.
- Considering the specification of the hyperspectral camera used here and assuming a range of 1.5 to 2.5 km, the ground pixel size would be approximately 2–4 m. This will pose a problem for the matching of datasets if the photogrammetric point cloud is too high in spatial resolution (i.e., cm pixel size in this study). As a solution, the point cloud can be downscaled (resampled) for finding transformation matrix and later be used with the original scale to perform geological mapping.
- Overall, the advantages of the method clearly outweigh the limitations, if those are considered during data processing and taken into account for the interpretation of the results.
5. Conclusions
- The SIFT image-matching algorithm performs reliable matching between the two image sets acquired from different viewpoints and with different spatial resolution and geometric projections (i.e., spectral data with aerial high-oblique stereo-images collected from a helicopter or near-horizontal stereo-images collected from a vessel using hand-held digital cameras).
- Larger vessels provide a more stable platform for data acquisition (i.e., less pronounced pitch and heave result in less distortion in the HSI data). Nevertheless, the presented method can cope with the data captured from both small and large vessels.
- The spectral mapping of hyperspectral imagery of vertical cliffs is not straightforward because of: (a) the relatively shallow absorption features of surface minerals in the spectra; (b) the instrument artifacts present in the data; and (c) the lack of ground samples of surface materials.
- Despite the low number of mineralogy related characteristic absorption features in the SWIR spectral range, a differentiation of lithological end-members is possible due to small differences in the slope, convexity and intensity of the reflectance spectra.
- Three methods are deployed to make an assessment of the information content of the hyperspectral images and the group of minerals present in the images: Mapping the wavelength position of the deepest absorption features between 2100 and 2400 nm provides a useful method for exploratory analysis of the surface mineralogy of vertical cliffs. By using a MNF transformation, it is possible to assess the material spatial variability, define end-members and employ a supervised classification. The SAM method provides information on the diversity and composition of minerals and their occurrences on the surface. However, assigning pixels to mineral classes could cause a loss of information.
- The empirical line correction method assumes that there are no differences in illumination across the image; therefore, changes in radiance due to cloud shadowing or topography are not corrected. In addition to sensor and platform/specific geometric distortion corrections, a subsequent topographic correction is highly recommended for sites with high relief or sub/optimal illumination conditions during data acquisition. Using continuum removal in a wavelength mapping technique reduces shadow effects and differences in scene illumination, which enables the production of seamless map products. However, by doing so, the spectral albedo, which links to the brightness of an object, is discarded. More importantly, the overall reflectance is also a key to handle mapping of spectrally featureless minerals.
- The method also assumes that the effect of the atmosphere is uniform across the image, but it has been observed that atmospheric constituents, especially water vapor, can vary greatly over short distances.
- The method assumes that the earth’s surface consists of Lambertian reflectors, when in fact the surfaces possess bi-directional reflectance properties [98,99], which will cause viewing geometry to be an important control over the accuracy of the prediction equations. Non-Lambertian reflectance is largely due to the presence of shadows caused by surface micro-relief. Further development of the methodology will require consideration of the bi-directional reflectance properties of the targets, and measurement of the spatial variability of the atmospheric path radiance throughout the image.
- The choice of the reference spectrum for removing the effect of atmosphere between the vessel and the outcrop has a high influence on the quality of the spectral data and needs to be investigated carefully, as it can otherwise create non-atmospheric absorption features. The reference spectra should be selected: (a) from homogeneous extensive bare areas (at least several times the size of the sensor ground instantaneous field-of-view) that are preferably located vertically; (b) devoid of vegetation or other temporally variant features; and (c) ideally spectrally featureless.
- Finally, we experienced that more accurate results can be achieved, if a perpendicular view to the surface of outcrop is set for data acquisition and a view-based projection of 3D point cloud onto 2D pseudo-orthophotos is used to project the individual hyperspectral products on the 2D pseudo-orthophoto. Exploiting inaccurate viewing angle would complicate the matching process of the two image-sets, thereby inducing distortions in the resulting georeferenced hyperspectral scan, and therefore will have possible impacts on the final mapping results.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Sørensen, E.V. Implementation of Digital Multi-Model Photogrammetry for Building of 3D-Models and Interpretation of the Geological and Tectonic Evolution of the Nuussuaq Basin. Ph.D. Thesis, University of Copenhagen, Copenhagen, Denmark, 2011. [Google Scholar]
- Svennevig, K.; Guarnieri, P.; Stemmerik, L. From oblique photogrammetry to a 3d model–structural modeling of Kilen, eastern north Greenland. Comput. Geosci. 2015, 83, 120–126. [Google Scholar] [CrossRef]
- Sørensen, E.V.; Bjerager, M.; Citterio, M. Digital models based on images taken with handheld cameras–examples on land, from the sea and on ice. Geol. Surv. Den. Greenl. Bull. 2015, 73–76. [Google Scholar]
- Sørensen, E.V.; Pedersen, A.K.; García-Sellés, D.; Strunck, M.N. Point clouds from oblique stereo-imagery: Two outcrop case studies across scales and accessibility. Eur. J. Remote Sens. 2015, 48, 593–614. [Google Scholar] [CrossRef]
- Vosgerau, H.; Guarnieri, P.; Weibel, R.; Larsen, M.; Dennehy, C.; Sørensen, E.V.; Knudsen, C. Study of a palaeogene intrabasaltic sedimentary unit in southern east Greenland: From 3-d photogeology to micropetrography. Geol. Surv. Den. Greenl. Bull. 2010, 20, 75–78. [Google Scholar]
- Óskarsson, B.V.; Andersen, C.B.; Riishuus, M.S.; Sørensen, E.V.; Tegner, C. The mode of emplacement of neogene flood basalts in eastern Iceland: The plagioclase ultraphyric basalts in the grænavatn group. J. Volcanol. Geother. Res. 2017, 332, 26–50. [Google Scholar] [CrossRef]
- Vosgerau, H.; Passey, S.R.; Svennevig, K.; Strunck, M.N.; Jolley, D.W. Reservoir architectures of interlava systems: A 3d photogrammetrical study of eocene cliff sections, Faroe Islands. Geol. Soc. Lond. Spec. Publ. 2016, 436, 55–73. [Google Scholar] [CrossRef]
- Buckley, S.; Vallet, J.; Braathen, A.; Wheeler, W. Oblique helicopter-based laser scanning for digital terrain modelling and visualisation of geological outcrops. In Proceedings of the International Archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Beijing, China, 3–11 July 2008; Volume 37, pp. 493–498. [Google Scholar]
- Vallet, J.; Skaloud, J. Development and experiences with a fully-digital handheld mapping system operated from a helicopter. In Proceedings of the XX ISPRS Congress, Istanbul, Turkey, 12–23 July 2004; Volume XXXV. [Google Scholar]
- Pedersen, A.K.; Larsen, L.M.; Pedersen, G.K.; Dueholm, K.S. Five slices through the Nuussuaq basin, west Greenland. Geol. Surv. Den. Greenl. Bull. 2006, 10, 53–56. [Google Scholar]
- Svennevig, K.; Guarnieri, P. From 3d mapping to 3d modelling: A case study from the skaergaard intrusion, southern east Greenland. Geol. Surv. Den. Greenl. Bull. 2012, 26, 57–60. [Google Scholar]
- Pedersen, A.; Watt, M.; Watt, W.; Larsen, L. Structure and stratigraphy of the early tertiary basalts of the Blosseville Kyst, east Greenland. J. Geol. Soc. 1997, 154, 565–570. [Google Scholar] [CrossRef]
- Bellian, J.A.; Kerans, C.; Jennette, D.C. Digital outcrop models: Applications of terrestrial scanning lidar technology in stratigraphic modeling. J. Sediment. Res. 2005, 75, 166–176. [Google Scholar] [CrossRef]
- Buckley, S.J.; Howell, J.A.; Enge, H.D.; Kurz, T.H. Terrestrial laser scanning in geology: Data acquisition, processing and accuracy considerations. J. Geol. Soc. 2008, 165, 625–638. [Google Scholar] [CrossRef]
- Buckley, S.J.; Enge, H.D.; Carlsson, C.; Howell, J.A. Terrestrial laser scanning for use in virtual outcrop geology. Photogramm. Rec. 2010, 25, 225–239. [Google Scholar] [CrossRef]
- Buckley, S.J.; Howell, J.A.; Enge, H.D.; Leren, B.L.S.; Kurz, T.H. Integration of terrestrial laser scanning, digital photogrammetry and geostatistical methods for high-resolution modelling of geological outcrops. Remote Sens. Spat. Inf. Sci. 2006, 36, 6. [Google Scholar]
- Enge, H.D.; Buckley, S.J.; Rotevatn, A.; Howell, J.A. From outcrop to reservoir simulation model: Workflow and procedures. Geosphere 2007, 3, 469–490. [Google Scholar] [CrossRef]
- Crowley, J.K. Visible and near-infrared spectra of carbonate rocks: Reflectance variations related to petrographic texture and impurities. J. Geophys. Res. Solid Earth 1986, 91, 5001–5012. [Google Scholar] [CrossRef]
- Gaffey, S.J. Spectral reflectance of carbonate minerals in the visible and near infrared (O.35-2.55 microns); calcite, aragonite, and dolomite. Am. Mineral. 1986, 71, 151–162. [Google Scholar]
- Hunt, G.R.; Salisbury, J.W. Visible and near infrared spectra of minerals and rocks. II. Carbonates. Mod. Geol. 1971, 2, 23–30. [Google Scholar]
- Van der Meer, F. Spectral reflectance of carbonate mineral mixtures and bidirectional reflectance theory: Quantitative analysis techniques for application in remote sensing. Remote Sens. Rev. 1995, 13, 67–94. [Google Scholar] [CrossRef]
- Van der Meer, F. Spectral mixture modelling and spectral stratigraphy in carbonate lithofacies mapping. ISPRS J. Photogramm. Remote Sens. 1996, 51, 150–162. [Google Scholar] [CrossRef]
- Van der Meer, F.D.; De Jong, S.M. Imaging Spectrometry: Basic Principles and Prospective Applications; Springer Science & Business Media: Berlin/Heidelberg, Germany, 2011; Volume 4. [Google Scholar]
- Solomon, J.; Rock, B. Imaging spectrometry for earth remote sensing. Science 1985, 228, 1147–1152. [Google Scholar]
- Bellian, J.A.; Beck, R.; Kerans, C. Analysis of hyperspectral and lidar data: Remote optical mineralogy and fracture identification. Geosphere 2007, 3, 491–500. [Google Scholar] [CrossRef]
- Bowen, B.B.; Martini, B.A.; Chan, M.A.; Parry, W.T. Reflectance spectroscopic mapping of diagenetic heterogeneities and fluid-flow pathways in the Jurassic Navajo sandstone. AAPG Bull. 2007, 91, 173–190. [Google Scholar] [CrossRef]
- Harris, J.R.; Rogge, D.; Hitchcock, R.; Ijewliw, O.; Wright, D. Mapping lithology in canada’s arctic: Application of hyperspectral data using the minimum noise fraction transformation and matched filtering. Can. J. Earth Sci. 2005, 42, 2173–2193. [Google Scholar] [CrossRef]
- Windeler, D.; Lyon, R. Discrimination dolomitization of marble in the Ludwig skarn near yerington, Nevada using high-resolution airborne infrared imagery. Photogramm. Eng. Remote Sens. 1991, 57, 1171–1177. [Google Scholar]
- Bedini, E. Mapping lithology of the sarfartoq carbonatite complex, southern west Greenland, using hymap imaging spectrometer data. Remote Sens. Environ. 2009, 113, 1208–1219. [Google Scholar] [CrossRef]
- Bedini, E. Mineral mapping in the Kap Simpson complex, central east Greenland, using hymap and aster remote sensing data. Adv. Space Res. 2011, 47, 60–73. [Google Scholar] [CrossRef]
- Bedini, E. Mapping alteration minerals at malmbjerg molybdenum deposit, central east Greenland, by kohonen self-organizing maps and matched filter analysis of hymap data. Int. J. Remote Sens. 2012, 33, 939–961. [Google Scholar] [CrossRef]
- Tukiainen, T.; Thomassen, B. Application of airborne hyperspectral data to mineral exploration in north-east Greenland. Geol. Surv. Den. Greenl. Bull. 2010, 20, 71–74. [Google Scholar]
- Bedini, E.; Tukiainen, T. Using spectral mixture analysis of hyperspectral remote sensing data to map lithology of the sarfartoq carbonatite complex, southern west Greenland. Geol. Surv. Den. Greenl. Bull 2009, 17, 69–72. [Google Scholar]
- Salehi, S.; Jakob, S.; Gloaguen, R.; Fensholt, R. Multiscale hyperspectral analysis of lithologies in presence of abundant lichens and mapping of ultramafic rocks in western Greenland (innarsuaq). In Proceedings of the 10th EARSeL SIG Imaging Spectroscopy Workshop, Zurich, Switzerland, 19–21 April 2017. [Google Scholar]
- Kurz, T.H.; Buckley, S.J.; Howell, J.A. Close-range hyperspectral imaging for geological field studies: Workflow and methods. Int. J. Remote Sens. 2013, 34, 1798–1822. [Google Scholar] [CrossRef]
- Kurz, T.H.; Dewit, J.; Buckley, S.J.; Thurmond, J.B.; Hunt, D.W.; Swennen, R. Hyperspectral image analysis of different carbonate lithologies (limestone, karst and hydrothermal dolomites): The pozalagua quarry case study (Cantabria, north-west Spain). Sedimentology 2012, 59, 623–645. [Google Scholar] [CrossRef]
- Murphy, R.J.; Monteiro, S.T. Mapping the distribution of ferric iron minerals on a vertical mine face using derivative analysis of hyperspectral imagery (430–970 nm). ISPRS J. Photogramm. Remote Sens. 2013, 75, 29–39. [Google Scholar] [CrossRef]
- Murphy, R.J.; Monteiro, S.T.; Schneider, S. Evaluating classification techniques for mapping vertical geology using field-based hyperspectral sensors. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3066–3080. [Google Scholar] [CrossRef]
- Buckley, S.J.; Kurz, T.H.; Howell, J.A.; Schneider, D. Terrestrial lidar and hyperspectral data fusion products for geological outcrop analysis. Comput. Geosci. 2013, 54, 249–258. [Google Scholar] [CrossRef]
- Zhang, Q.; Pless, R. Extrinsic calibration of a camera and laser range finder (improves camera calibration). In Proceedings of the IEEE/RSJ International Conference on Intelligent Robots and Systems (IROS 2004), Sendai, Japan, 28 September–2 October 2004; pp. 2301–2306. [Google Scholar]
- Kurz, T.H.; Buckley, S.J.; Howell, J.A.; Schneider, D. Integration of panoramic hyperspectral imaging with terrestrial lidar data. Photogramm. Rec. 2011, 26, 212–228. [Google Scholar] [CrossRef]
- Sima, A.A.; Buckley, S.J.; Kurz, T.H.; Schneider, D. Semi-automated registration of close-range hyperspectral scans using oriented digital camera imagery and a 3d model. Photogramm. Rec. 2014, 29, 10–29. [Google Scholar] [CrossRef]
- Monteiro, S.T.; Nieto, J.; Murphy, R.; Ramakrishnan, R.; Taylor, Z. Combining strong features for registration of hyperspectral and lidar data from field-based platforms. In Proceedings of the 2013 IEEE International Conference on Geoscience and Remote Sensing Symposium (IGARSS), Melbourne, Australia, 21–26 July 2013; pp. 1210–1213. [Google Scholar]
- Kurz, T.; Buckley, S.; Howell, J.; Schneider, D. Geological outcrop modelling and interpretation using ground based hyperspectral and laser scanning data fusion. In Proceedings of the International archives of Photogrammetry, Remote Sensing and Spatial Information Sciences, Beijing, China, 3–11 July 2008; Volume 37, pp. 1229–1234. [Google Scholar]
- Jakob, S.; Zimmermann, R.; Gloaguen, R. The need for accurate geometric and radiometric corrections of drone-borne hyperspectral data for mineral exploration: Mephysto—A toolbox for pre-processing drone-borne hyperspectral data. Remote Sens. 2017, 9, 88. [Google Scholar] [CrossRef]
- Grocott, J.; McCaffrey, K.J. Basin evolution and destruction in an early Proterozoic continental margin: The rinkian fold–thrust belt of central west Greenland. J. Geol. Soc. 2017, 174, 453–467. [Google Scholar] [CrossRef]
- Henderson, G.; Pulvertaft, T. Geological Map of Greenland, 1: 100000, Mârmorilik 71 v. 2 syd, Nûgâtsiaq 71 v. 2 Nord, Pangnertôq 72 v. 2 syd; Descriptive Text; Grønlands Geologiske Undersøgelse: Copenhagen, Denmark, 1987; Volume 8. [Google Scholar]
- Rosa, D.; Dewolfe, M.; Guarnieri, P.; Kolb, J.; LaFlamme, C.; Partin, C.; Salehi, S.; Vest Sørensen, E.; Thaarup, S.; Thrane, K.; et al. Architecture and Mineral Potential of the Paleoproterozoic Karrat Group, West Greenland. Results of the 2016 Season, 5; Geological Survey of Denmark and Greenland: Copenhagen, Denmark, 2017; p. 114. Available online: https://data.geus.dk/greenlanddb/webresources/dodex-report-file/released-report/32501 (accessed on 9 September 2017).
- Cadman, A.; Tarney, J.; Bridgwater, D.; Mengel, F.; Whitehouse, M.; Windley, B. The petrogenesis of the kangâmiut dyke swarm, W. Greenland. Precambrian Res. 2001, 105, 183–203. [Google Scholar] [CrossRef]
- Ramberg, H. Titanic iron ore formed by dissociation of silicates in granulite facies [Greenland]. Econ. Geol. 1948, 43, 553–570. [Google Scholar] [CrossRef]
- Bridgwater, D.; Mengel, F.; Fryer, B.; Wagner, P.; Hansen, S.C. Early Proterozoic mafic dykes in the north atlantic and baltic cratons: Field setting and chemistry of distinctive dyke swarms. Geol. Soc. Lond. Spec. Publ. 1995, 95, 193–210. [Google Scholar] [CrossRef]
- Ramberg, H. On the Petrogenesis of the Gneiss Complexes between Sukkertoppen and Christianshaab, West Greenland. Available online: http://2dgf.dk/xpdf/bull-1948-11-3-312-327.pdf (accessed on 9 September 2017).
- Escher, A.; Escher, J.; Watterson, J. The reorientation of the kangâmiut dike swarm, west Greenland. Can. J. Earth Sci. 1975, 12, 158–173. [Google Scholar] [CrossRef]
- Connelly, J.N.; Mengel, F.C. Evolution of Archean components in the paleoproterozoic Nagssugtoqidian orogen, west Greenland. Geol. Soc. Am. Bull. 2000, 112, 747–763. [Google Scholar] [CrossRef]
- Engström, J.; Klint, K.E.S. Continental collision structures and post-orogenic geological history of the kangerlussuaq area in the southern part of the nagssugtoqidian orogen, central west Greenland. Geosciences 2014, 4, 316–334. [Google Scholar] [CrossRef]
- Rosa, D.; Guarnieri, P.; Hollis, J.; Kolb, J.; Partin, C.; Petersen, J.; Vest Sørensen, E.; Thomassen, B.; Thomsen, L.; Thrane, K. Architecture and Mineral Potential of the Paleoproterozoic Karrat Group, West Greenland; Results of the 2015 Season; Geological Survey of Denmark and Greenland: Copenhagen, Denmark, 2016; p. 98. [Google Scholar]
- Dueholm, K.S. Geologic photogrammetry using standard small-frame cameras. Grønl. Geol. Unders. 1992, 156, 7–17. [Google Scholar]
- Lowe, D.G. Object recognition from local scale-invariant features. In Proceedings of the seventh IEEE International Conference on Computer Vision, Kerkyra, Greece, 20–27 September 1999; pp. 1150–1157. [Google Scholar]
- Fischler, M.A.; Bolles, R.C. Random sample consensus: A paradigm for model fitting with applications to image analysis and automated cartography. Commun. ACM 1981, 24, 381–395. [Google Scholar] [CrossRef]
- Lorenz, S.; Salehi, S.; Kirsch, M.; Zimmermann, R.; Unger, G.; Gloaguen, R. Radiometric correction and 3d integration of long-range ground-based hyperspectral imagery for mineral exploration of vertical outcrops. submitted.
- Smith, G.M.; Milton, E.J. The use of the empirical line method to calibrate remotely sensed data to reflectance. Int. J. Remote Sens. 1999, 20, 2653–2662. [Google Scholar] [CrossRef]
- Chavez, P.S. Image-based atmospheric corrections-revisited and improved. Photogramm. Eng. Remote Sens. 1996, 62, 1025–1035. [Google Scholar]
- Vicente-Serrano, S.M.; Pérez-Cabello, F.; Lasanta, T. Assessment of radiometric correction techniques in analyzing vegetation variability and change using time series of landsat images. Remote Sens. Environ. 2008, 112, 3916–3934. [Google Scholar] [CrossRef]
- Wessman, C.A.; Bateson, C.; Curtiss, B.; Benning, T.L. A comparison of spectral mixture analysis an ndvi for ascertaining ecological variables. In Proceedings of the 4th Annual JPL Airborne Geoscience Workshop, Washington, DC, USA, 25–29 October 1993. [Google Scholar]
- Haralick, R.M.; Sternberg, S.R.; Zhuang, X. Image analysis using mathematical morphology. IEEE Trans. Pattern Anal. Mach. Intell. 1987, 532–550. [Google Scholar] [CrossRef]
- Savitzky, A.; Golay, M.J. Smoothing and differentiation of data by simplified least squares procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Pollefeys, M.; Van Gool, L.; Vergauwen, M.; Verbiest, F.; Cornelis, K.; Tops, J.; Koch, R. Visual modeling with a hand-held camera. Int. J. Comput. Vis. 2004, 59, 207–232. [Google Scholar] [CrossRef]
- Saaidi, A.; Karam, A.; Satori, K. Incremental multi-view 3d reconstruction starting from two images taken by a stereo pair of cameras. 3D Res. 2015, 6, 1–18. [Google Scholar]
- Böhm, J.; Becker, S. Automatic marker-free registration of terrestrial laser scans using reflectance. In Proceedings of the 8th Conference on Optical 3D Measurement Techniques, Zurich, Switzerland, 9–12 July 2007; pp. 338–344. [Google Scholar]
- Delponte, E.; Isgrò, F.; Odone, F.; Verri, A. Svd-matching using sift features. Graph. Models 2006, 68, 415–431. [Google Scholar] [CrossRef]
- Khan, N.Y.; McCane, B.; Wyvill, G. Sift and surf performance evaluation against various image deformations on benchmark dataset. In Proceedings of the 2011 International Conference on Digital Image Computing Techniques and Applications (DICTA), Noosa, Australia, 6–8 December 2011; pp. 501–506. [Google Scholar]
- Lingua, A.; Marenchino, D.; Nex, F. Performance analysis of the sift operator for automatic feature extraction and matching in photogrammetric applications. Sensors 2009, 9, 3745–3766. [Google Scholar] [CrossRef] [PubMed]
- Meierhold, N.; Spehr, M.; Schilling, A.; Gumhold, S.; Maas, H. Automatic feature matching between digital images and 2d representations of a 3d laser scanner point cloud. In Proceedings of the International Archives of the Photogrammetry, Remote Sensing and Spatial Information Sciences, Newcastle upon Tyne, UK, 21–24 June 2010; Volume 38, pp. 446–451. [Google Scholar]
- Wessel, B.; Huber, M.; Roth, A. Registration of near real-time SAR images by image-to-image matching. Photogramm. Image Anal. 2007, 3, 179–184. [Google Scholar]
- Yun, S.; Min, D.; Sohn, K. 3D scene reconstruction system with hand-held stereo cameras. In Proceedings of the 3DTV Conference, Kos Island, Greece, 7–9 May 2007; pp. 1–4. [Google Scholar]
- Sima, A.; Buckley, S.J.; Kurz, T.H.; Schneider, D. Semi-automatic integration of panoramic hyperspectral imagery with photorealistic lidar models. Photogramm. Fernerkund. Geoinf. 2012, 2012, 443–454. [Google Scholar] [CrossRef]
- Sima, A.A.; Buckley, S.J. Optimizing sift for matching of short wave infrared and visible wavelength images. Remote Sens. 2013, 5, 2037–2056. [Google Scholar] [CrossRef]
- Muja, M.; Lowe, D.G. Fast approximate nearest neighbors with automatic algorithm configuration. In Proceedings of the International Joint Conference on Computer Vision, Imaging and Computer Graphics Theory and Applications, Lisbon, Portugal, 5–8 February 2009; Volume 2, p. 2. [Google Scholar]
- Van der Meer, F.; Kopačková, V.; Koucká, L.; van der Werff, H.M.; van Ruitenbeek, F.J.; Bakker, W.H. Wavelength feature mapping as a proxy to mineral chemistry for investigating geologic systems: An example from the rodalquilar epithermal system. Int. J. Appl. Earth Obs. Geoinf. 2018, 64, 237–248. [Google Scholar] [CrossRef]
- Joseph, W. Automated spectral analysis: A geologic example using aviris data, north grapevine mountains, nevada. In Proceedings of the Tenth Thematic Conference on Geologic Remote Sensing, Environmental Research Institute of Michigan, San Antonio, TX, USA, 9–12 May 1994; pp. 1407–1418. [Google Scholar]
- Green, A.A.; Berman, M.; Switzer, P.; Craig, M.D. A transformation for ordering multispectral data in terms of image quality with implications for noise removal. IEEE Trans. Geosci. Remote Sens. 1988, 26, 65–74. [Google Scholar] [CrossRef]
- Boardman, J. Automated spectral unmixing of aviris data using convex geometry concepts. In Proceedings of the Annual JPL Airborne Geosciences Workshop, Washington, DC, USA, 25–29 October 1993; JPL Publication: Pasadena, CA, USA, 1993. [Google Scholar]
- Kruse, F.A.; Lefkoff, A.; Boardman, J.; Heidebrecht, K.; Shapiro, A.; Barloon, P.; Goetz, A. The spectral image processing system (sips)-interactive visualization and analysis of imaging spectrometer data. Remote Sens. Environ. 1993, 44, 145–163. [Google Scholar] [CrossRef]
- Pontual, S.; Merry, N.; Gamson, P. G-mex. In Spectral Interpretation Field Manual; Ausspec International Pty. Ltd.: Kew, Australia, 1997; Volume 1, p. 3101. [Google Scholar]
- Thompson, A.J.; Hauff, P.L.; Robitaille, A.J. Alteration mapping in exploration: Application of short wave infrared (swir) spectroscopy. SEG Newsl. 1999, 39, 1–27. [Google Scholar]
- Clark, R.N. Spectroscopy of rocks and minerals, and principles of spectroscopy. In Manual of Remote Sensing, Volume 3, Remote Sensing for the Earth Sciences; John Wiley and Sons: New York, NY, USA, 1999; pp. 3–58. Available online: https://speclab.cr.usgs.gov/PAPERS.refl-mrs/ (accessed on 5 January 2018).
- Clark, R.N.; King, T.V.; Klejwa, M.; Swayze, G.A.; Vergo, N. High spectral resolution reflectance spectroscopy of minerals. J. Geophys. Res. Solid Earth 1990, 95, 12653–12680. [Google Scholar] [CrossRef]
- Bishop, J.; Lane, M.; Dyar, M.; Brown, A. Reflectance and emission spectroscopy study of four groups of phyllosilicates: Smectites, kaolinite-serpentines, chlorites and micas. Clay Miner. 2008, 43, 35–54. [Google Scholar] [CrossRef]
- Clark, R.N.; Roush, T.L. Reflectance spectroscopy: Quantitative analysis techniques for remote sensing applications. J. Geophys. Res. Solid Earth 1984, 89, 6329–6340. [Google Scholar] [CrossRef]
- Ahmad, F. Pixel purity index algorithm and n-dimensional visualization for ETM+ image analysis: A case of district vehari. Glob. J. Hum. Soc. Sci. Arts Humanit. 2012, 12, 76–82. [Google Scholar]
- Salehi, S.; Rogge, D.; Rivard, B.; Heincke, B.H.; Fensholt, R. Modeling and assessment of wavelength displacements of characteristic absorption features of common rock forming minerals encrusted by lichens. Remote Sens. Environ. 2017, 199, 78–92. [Google Scholar] [CrossRef]
- Hunt, G.R.; Ashley, R.P. Spectra of altered rocks in the visible and near infrared. Econ. Geol. 1979, 74, 1613–1629. [Google Scholar] [CrossRef]
- Hunt, G.R.; Salisbury, J.W.; Lenhoff, C.J. Visible and near infrared spectra of minerals and rocks. VI. Additional silicates. Mod. Geol. 1973, 4, 85–106. [Google Scholar]
- King, T.V.; Clark, R.N. Spectral characteristics of chlorites and mg-serpentines using high-resolution reflectance spectroscopy. J. Geophys. Res. Solid Earth 1989, 94, 13997–14008. [Google Scholar] [CrossRef]
- McInerney, D.; Kempeneers, P. Image (re-) projections and merging. In Open Source Geospatial Tools; Springer: Berlin, Germnay, 2015; pp. 99–127. [Google Scholar]
- Sgavetti, M.; Pompilio, L.; Carli, C. Rock mineralogy and chemistry implications for spectral reflectance analysis. Mem. Soc. Astron. Ital. Suppl. 2007, 11, 155–158. [Google Scholar]
- Zaini, N.; van der Meer, F.; van der Werff, H. Determination of carbonate rock chemistry using laboratory-based hyperspectral imagery. Remote Sens. 2014, 6, 4149–4172. [Google Scholar] [CrossRef]
- Silva, L.F. Radiation and Instrumentation in Remote Sensing. Remote Sens. Quant. Approach 1978, 35–36. [Google Scholar]
- Jackson, R.; Teillet, P.; Slater, P.; Fedosejevs, G.; Jasinski, M.F.; Aase, J.; Moran, M. Bidirectional measurements of surface reflectance for view angle corrections of oblique imagery. Remote Sens. Environ. 1990, 32, 189–202. [Google Scholar] [CrossRef]











| Study | ID | X-Ortho (Pixels) | Y-Ortho | X-Fenix | Y-Fenix (Pixels) | Diff-X (Pixels) | Diff-Y (Pixels) |
|---|---|---|---|---|---|---|---|
| Karrat | CP 1 | 193.8593 | 193.8593 | 190.6042 | 517.9694 | 3.2552 | 2.9267 |
| CP 2 | 219.3461 | 219.3461 | 220.2049 | 300.3276 | −0.8589 | −11.1290 | |
| CP 3 | 350.2552 | 350.2552 | 357.8391 | 481.0251 | −7.5839 | 0.4825 | |
| CP 4 | 211.2367 | 211.2367 | 201.6286 | 802.7344 | 9.6081 | 0.8329 | |
| CP 5 | 21.24463 | 21.24463 | 35.28549 | 786.6907 | −14.0409 | 12.2430 | |
| CP 6 | 232.0895 | 232.0895 | 235.4142 | 214.2756 | −3.3247 | −13.1219 | |
| CP 7 | 381.5344 | 381.5344 | 380.6374 | 864.7964 | 0.8970 | −14.8896 | |
| CP 8 | 188.0669 | 188.0669 | 183.0522 | 954.3008 | 5.0147 | 3.3454 | |
| CP 9 | 98.86334 | 98.86334 | 94.81434 | 400.3867 | 4.0490 | 1.1852 | |
| CP 10 | 122.0331 | 122.0331 | 128.1674 | 746.1608 | −6.1343 | −2.8350 | |
| RSME-X | RSME-Y (pixels) | ||||||
| 6.7 | 8.4 | ||||||
| Søndre Strømfjord | CP 1 | 140.3506 | 922.3118 | 134.8122 | 915.8555 | 5.5383 | 6.4563 |
| CP 2 | 105.2719 | 880.0375 | 106.2451 | 877.352 | −0.9732 | 2.6855 | |
| CP 3 | 29.7179 | 713.6388 | 30.48011 | 719.6117 | −0.7622 | −5.9730 | |
| CP 4 | 265.3745 | 854.8528 | 266.0554 | 855.8231 | −0.6810 | −0.9703 | |
| CP 5 | 212.3068 | 642.582 | 215.5454 | 650.471 | −3.2387 | −7.8890 | |
| CP 6 | 343.6269 | 1202.941 | 350.5148 | 1204.425 | −6.8879 | −1.4839 | |
| CP 7 | 216.8041 | 1007.76 | 217.6155 | 1009.423 | −0.8115 | −1.6634 | |
| CP 8 | 161.9374 | 460.8926 | 162.9654 | 453.8132 | −1.0279 | 7.0793 | |
| CP 9 | 36.01406 | 415.9199 | 28.82405 | 415.7237 | 7.1900 | 0.1962 | |
| CP 10 | 265.3745 | 1056.33 | 268.1255 | 1057.449 | −2.7510 | −1.1189 | |
| RSME-X | RSME-Y (pixels) | ||||||
| 3.9 | 4.5 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Salehi, S.; Lorenz, S.; Vest Sørensen, E.; Zimmermann, R.; Fensholt, R.; Henning Heincke, B.; Kirsch, M.; Gloaguen, R. Integration of Vessel-Based Hyperspectral Scanning and 3D-Photogrammetry for Mobile Mapping of Steep Coastal Cliffs in the Arctic. Remote Sens. 2018, 10, 175. https://doi.org/10.3390/rs10020175
Salehi S, Lorenz S, Vest Sørensen E, Zimmermann R, Fensholt R, Henning Heincke B, Kirsch M, Gloaguen R. Integration of Vessel-Based Hyperspectral Scanning and 3D-Photogrammetry for Mobile Mapping of Steep Coastal Cliffs in the Arctic. Remote Sensing. 2018; 10(2):175. https://doi.org/10.3390/rs10020175
Chicago/Turabian StyleSalehi, Sara, Sandra Lorenz, Erik Vest Sørensen, Robert Zimmermann, Rasmus Fensholt, Bjørn Henning Heincke, Moritz Kirsch, and Richard Gloaguen. 2018. "Integration of Vessel-Based Hyperspectral Scanning and 3D-Photogrammetry for Mobile Mapping of Steep Coastal Cliffs in the Arctic" Remote Sensing 10, no. 2: 175. https://doi.org/10.3390/rs10020175
APA StyleSalehi, S., Lorenz, S., Vest Sørensen, E., Zimmermann, R., Fensholt, R., Henning Heincke, B., Kirsch, M., & Gloaguen, R. (2018). Integration of Vessel-Based Hyperspectral Scanning and 3D-Photogrammetry for Mobile Mapping of Steep Coastal Cliffs in the Arctic. Remote Sensing, 10(2), 175. https://doi.org/10.3390/rs10020175