Estimating Surface Downward Shortwave Radiation over China Based on the Gradient Boosting Decision Tree Method

Abstract

Downward shortwave radiation (DSR) is an essential parameter in the terrestrial radiation budget and a necessary input for models of land-surface processes. Although several radiation products using satellite observations have been released, coarse spatial resolution and low accuracy limited their application. It is important to develop robust and accurate retrieval methods with higher spatial resolution. Machine learning methods may be powerful candidates for estimating the DSR from remotely sensed data because of their ability to perform adaptive, nonlinear data fitting. In this study, the gradient boosting regression tree (GBRT) was employed to retrieve DSR measurements with the ground observation data in China collected from the China Meteorological Administration (CMA) Meteorological Information Center and the satellite observations from the Advanced Very High Resolution Radiometer (AVHRR) at a spatial resolution of 5 km. The validation results of the DSR estimates based on the GBRT method in China at a daily time scale for clear sky conditions show an R² value of 0.82 and a root mean square error (RMSE) value of 27.71 W·m⁻² (38.38%). These values are 0.64 and 42.97 W·m⁻² (34.57%), respectively, for cloudy sky conditions. The monthly DSR estimates were also evaluated using ground measurements. The monthly DSR estimates have an overall R² value of 0.92 and an RMSE of 15.40 W·m⁻² (12.93%). Comparison of the DSR estimates with the reanalyzed and retrieved DSR measurements from satellite observations showed that the estimated DSR is reasonably accurate but has a higher spatial resolution. Moreover, the proposed GBRT method has good scalability and is easy to apply to other parameter inversion problems by changing the parameters and training data.

1. Introduction

Downward shortwave radiation (DSR) is a key parameter in the land-atmosphere interaction, which largely controls human life and ecosystems due to its important role in energy cycles [1,2], the hydrological cycle [3,4], the carbon cycles [5,6], and solar energy utilizations [7,8,9,10,11,12,13]. Therefore, knowledge of DSR is essential for improving our understanding of the Earth’s climate and potential climatic changes [14]. A number of gridded global DSR products exist from remote sensing, reanalysis, and general circulation models (GCMs). Satellite remote sensing is one of the most practical ways to derive DSR measurements with relatively higher spatial resolution and accuracy.

Currently, DSR data can be obtained in three ways. The first is through collection from ground measurements. This method is characterized by high precision and uneven geographic distribution. The second is estimation from reanalysis data and simulations from GCMs, which have relatively low spatial resolution and accuracy [15,16,17]. Examples include the ERA-Interim provided by European Center for Medium-Range Weather Forecast (ECMWF), the Japanese 55-year Reanalysis (JRA-55) provided by Japan Meteorological Agency, and the Modern-Era Retrospective analysis for Research and Applications (MERRA) reanalysis dataset provided by NASA. The third way is retrieval from remote sensing data [18,19,20], which can provide spatio-temporal continuous DSR estimates with relatively higher precision. Commonly used remote sensing datasets of surface solar radiance include the Global Energy and Water Cycle Experiment-Surface Radiation Budget (GEWEX-SRB), the International Satellite Cloud Climatology Project-Flux Data (ISCCP-FD), the University of Maryland-Shortwave Radiation Budget (UMD-SRB), and the Earth’s Radiant Energy System (CERES). Each type of DSR data from a different source has advantages and limitations: the ground measurements provide accurate but sparse spatial coverage, whereas products from the two other methods may have larger uncertainties. The ground measurements are always used to evaluate the other two types of DSR estimates. GCMs are widely believed to have an advantage in simulating global scale climate changes [21]. A reanalysis product is a combination of a model and measurements. It uses observations to constrain the dynamic model to optimize complete coverage and accuracy [22]. DSR retrievals from remote sensing data always have a relatively higher accuracy than those from reanalysis data and simulations from GCMs. These DSR products have been widely evaluated using ground measurements [23,24,25,26]. For example, Zhang et al. [26] evaluated four current representative existing remote sensing products using 1151 sites from the Global Energy Balance Archive and the China Meteorological Administration (CMA). The results implied that DSR estimates from remotely sensed data were more accurate than those acquired from reanalysis and simulations from GCMs. The maximum spatial resolution of these four products is 0.5°, and the temporal resolution is thrice-hourly. Although the current global radiation products have finer temporal resolution, they have lower spatial resolutions, which limit their application [27]. Therefore, it is still necessary to generate higher spatial resolution DSR estimates using satellite observation.

Several algorithms have been developed for retrieving DSR measurements. The first way is to estimate DSR based on statistical models [28,29,30,31,32,33]. Perez et al. [31] developed a simple solar radiation forecast model using sky cover predictions. Yang et al. [32] used a hybrid model with CMA routine data to estimate DSR, and the validation results of this proposed model against ground measurements collected in Tibetan Plateau were better than satellite estimations from existing satellite products. Wang et al. [33] used a statistical model to establish the relationship between top of atmosphere (TOA) reflectance and net surface shortwave radiation using multiple regression and revised methods, and they then compared the precision of these methods using various parameters. Empirical statistical models usually construct a regression model directly using observed data and measured DSR values. These models are easy to apply but are disadvantaged by their lack of universality; the relationship established in a particular atmospheric condition or region may not be applicable in another area. The second method to retrieve DSR measurements is to estimate them based on parametric physical modeling methods [34,35,36,37,38,39]. Li et al. [37] proposed a parameterized model in which the normalized net surface shortwave radiation flux of the top incident irradiance of the atmosphere was used to establish a parametric relationship with the planetary albedo. Qin et al. [38] used satellite atmospheric and land products—including ozone thickness, precipitable water, aerosol loading, cloud water path, clouds effective particle radius, cloud fraction, and ground surface albedo—to establish a physically based parameterization model. They then used the model to estimate surface solar irradiance with a mean RMSE of approximately 100 W/m² and 35 W/m² on an instantaneous and daily mean basis, respectively. López et al. [39] proposed a new, simple parametric physical model to estimate global solar radiance under cloudy sky conditions. These methods often construct a physical model by simulating direct interaction between solar radiation and the atmosphere. This requires many parameters (e.g., aerosol optical depth, surface albedo, and moisture). It is obvious that model accuracy depends on these parameters.

Machine learning methods, which learn the relationship between inputs and outputs by fitting a flexible model directly from the data, are some of the most widely used methods to estimate DSR [40,41,42,43,44,45]. Wang [43] proposed a method try to derive DSR measurements using Moderate Resolution Imaging Spectroradiometer (MODIS) data (e.g., atmospheric profile product and surface reflectance) based on an artificial neural network (ANN) model. The validation results against ground measurements showed that the maximum root mean square error (RMSE) was less than 45 W·m⁻². Qin et al. [44] used an ANN-based method to establish the relationship between the measured monthly mean of daily global solar radiation levels and available remote sensing products with the aim of estimating global solar radiation. Zhou et al. [45] suggested that the Random Forest (RF) model was another feasible way to estimate DSR using satellite observations. These machine learning methods have their own advantages and disadvantages. For example, the attractiveness of an ANN is nonlinearity and high parallelism [46], and the RF cannot extrapolate beyond the training data and may not interpret well for conditions with few samples [47]. Although machine learning may provide powerful methods for estimating DSR from remote sensing data due to their ability to perform adaptive and nonlinear data fitting [48,49,50], the accuracy of the results is limited and many machine learning methods are prone to the phenomenon of overfitting. This can be avoid by using the gradient boosting regression tree (GBRT) method [51]. In addition, the GBRT can efficiently provide high accuracy. However, it has not been widely used for estimating DSR.

The objective of this study is to use a machine learning method, the GBRT, to obtain high accuracy DSR estimates from remote sensing and surface observed data under both clear and cloudy sky conditions in China. Moreover, this study aims to compare the DSR estimates from the GBRT with estimated values from classical ANN and existing remote sensing and reanalysis data.

The paper is organized as follows: Section 2 provides a brief introduction to the ground measurement and remote sensing data used. Section 2 also describes the methods used. Section 3 presents the results and an analysis. The conclusions are presented in Section 4.

2. Materials and Methods

2.1. Materials

2.1.1. Ground Measurements

The measurements of daily DSR used in this study were supplied by the CMA Meteorological Information Center. DSR was first measured in 1957, and its measurement was gradually collected at a total of 122 stations. However, the measurement at some stations have stopped sometime in the past. In 1994, there were 96 stations remaining to measure DSR. Quality control of the CMA DSR data was performed before the release; this included a spatial and temporal consistency check and manual inspection and correction [52]. Previous studies showed that the systematic errors in radiation measurements due to technical failure and operation-related problems are not rare [53,54]. Hence, a critical quality control procedure was performed to the ground measurements from the CMA before they were used in this study. The procedure is as described by Zhang [26]. Figure 1 shows the geographical distributions of the sites from the CMA. For more detailed information about the radiation data, it is possible to refer to the data description at the website http://data.cma.cn/.

This study used the daily DSR data collected from 96 radiation stations in China from 2001 to 2003. The daily DSR data from 2001 and 2002 were used to train the models, and the daily DSR data from 2003 was used to validate the model.

2.1.2. Satellite Data

The National Oceanic and Atmospheric Administration (NOAA) Climate Data Records (CDR) of Visible and Near Infrared Reflectance from the Advanced Very High Resolution Radiometer (AVHRR) and the NASA Langley Research Center (LaRC) Cloud and Clear Sky Radiation Properties dataset were used in the paper. The two satellite datasets are from the Advanced Very High Resolution Radiometer (AVHRR) Global Area Coverage (GAC) Level 1B data, which has been quality controlled. These were taken from the NOAA-16 sun-synchronous orbit satellite observations provided by the NOAA CDR program. The NASA LaRC Cloud and Clear Sky Radiation Properties dataset is generated using the CERES Cloud Mask and Cloud Property Retrieval System (CCPRS) [55]. The NOAA CDR of Visible and Near Infrared Reflectance from AVHRR was calibrated by a multiple invariant Earth target calibration approach [56,57]. The NASA LaRC Cloud and Clear Sky Radiation Properties dataset was generated using algorithms initially designed for application to the Tropical Rainfall Measurement Mission (TRMM) and Moderate Resolution Imaging Spectroradiometer (MODIS) imagery within the NASA Clouds and the Earth’s Radiant Energy System (CERES) program [58]. The spatial and temporal resolution of the dataset is about 4 km at the nadir and one day, respectively. Variables of the radiation properties dataset include cloud and clear sky pixel detection, cloud optical depth, cloud particle effective radius, land and sea surface temperature retrieval, shortwave broadband albedo, etc. [58]. Two variables including the calibrated 0.63 micron channel reflectance (channel 1) and the calibrated 0.86 micron channel reflectance (channel 2) were utilized for DSR estimation in this study [59].

Table 1. Input settings of the GBRT-based downward shortwave radiation (DSR) clear and cloudy sky models.

Inputs Data	Model	Unit	Range
Solar zenith angle	Clear and cloudy sky	Degrees	0–180
Viewing zenith angle	Clear and cloudy sky	Degrees	0–90
Relative azimuth angle	Clear and cloudy sky	Degrees	0–180
Top of atmosphere shortwave broadband albedo	Clear and cloudy sky	N/A	0–1.5
Reflectance of channel 1 and 2 of AVHRR	Clear and cloudy sky	Percent	0–12.5
Brightness temperature of channel 4 and 5 of AVHRR	Clear and cloudy sky	Degrees/Kelvins	160–340
Cloud optical depth	Cloudy sky	N/A	0–150
Cloud mask	Clear and cloudy sky	N/A	0–1

lists the corresponding information extracted from the AVHRR dataset used in this study.

2.1.3. DSR Products

The two DSR products, the MERRA and the GEWEX-SRB DSR, were used in the paper. The MERRA product is a second reanalysis project from NASA for the satellite era (i.e., from 1979 to the present) using an updated new version of the Goddard Earth Observing System Data Assimilation System Version 5 (GEOS-5) [60]. The spatial resolution of the daily MERRA DSR estimate is 0.5° × 0.667°. The GEWEX-SRB radiation product from remotely sensed data used here was from the NASA/GEWEX-SRB shortwave version 3.0. The primary inputs to produce the data include shortwave and longwave radiances derived from International Satellite Cloud Climatology Project (ISCCP) pixel-level (DX) data, cloud and surface properties derived from the same source, temperature and moisture profiles, etc. [61]. The GEWEX-SRB DSR product was provided with a temporal resolution of 1 day and a spatial resolution of 1° from July 1983 to December 2008.

2.2. Methods

2.2.1. Gradient Boosting Regression Tree

The GBRT is a powerful, advanced statistical method widely used in classification and prediction. Because it does not require making assumptions on the data, it is extensively used in certain fields, such as in the optimization of recommendation systems [62,63], visual tracking algorithms [64], and traffic systems [65,66,67,68]. The attractiveness of GBRT comes from its ability to deal with the uneven distribution of data attributes, its lack of limitation for any hypothesis of input data, its better predictive capacity than a single decision tree, its power to deal with larger data size, and its transparency in terms of model development.

The GBRT produces competitive, highly robust, and interpretable procedures for both regression and classification. This was a method first proposed by Friedeman [51]. The core idea of this model is to generate a strong classifier by constructing an M amount of different weak classifiers through multiple iterations in order to reach the final combination. Each iteration is designed to improve the previous result by reducing the residuals of the previous model and establishing a new combination model in the gradient direction of the residual reduction. To describe the accuracy of the model, a loss function defined as L(y, F) is introduced. The frequently employed loss functions include squared-error and absolute error [51]. Suppose that ${\{x_i,y_i\}}_{i=1}^N$ is the training sample. The x represents explanatory variables. The y represents the response variable. N is the number of the training sample. Let the M different individual decisions trees be represented by ${\{h(x;{\alpha }_i)\}}_{i=1}^M$, which is the parameterized function of the explanatory variables x and is characterized by ${\alpha =\{{\alpha }_m\}}_{m=1}^M$. β is the weight of each classifier, and α is the classifier parameter. Each tree divides the input space into the number of independent areas numbered J, as in R_1m, …, R_jm. Each R_jm has a corresponding predicted value γ_jm. If the x-value is in the area R_jm, it means x∈ R_jm and the constant I equals 1. However, the constant I = 0. Hence, the function (F(x)), which is an approximation function of the response variable. It can be written as follows:

$$\begin{array}{l}\{\begin{array}{l}F(x)={\displaystyle \sum _{m=1}^M{\beta }_{m}h(x;{\alpha }_m)}\\ h(x;{\alpha }_m)={\displaystyle \sum _{j=1}^J{\gamma }_{jm}I(x\in R_{jm}),whereI=1ifx\in R_{jm};I=0,\mathrm{otherwise}}\end{array}\\ \end{array}$$

(1)

The general process of GBRT shown in Figure 2 and more detail of GBRT can be find in Hastie et al. [69] and Ridgeway [70].

The GBRT model can be constructed in three steps: (1) the preparation of the training database, (2) the architecture design and training phase, and (3) the application of the GBRT method. The next step is then to divide the data into clear sky and cloudy sky conditions according to the NOAA CDR of cloud mask data. If the pixel was marked as “cloud” by AVHRR data, it means it is under cloudy conditions. Otherwise, there is clear sky conditions. The GBRT-based DSR clear and cloudy sky model were trained using cloud mask data provided by the AVHRR data.

The performance of the DSR estimates was tested using the holdout method, which is a simple type of cross-validation. The dataset was randomly stratified into two groups, with 80% made part of the training dataset and 20% made part of the testing dataset. The main procedures are as follows.

(1)

Extracting the TOA radiance from the NOAA CDR of Visible and Near Infrared Reflectance from AVHRR;

(2)

Extracting the cloud properties from the NASA LaRC Cloud and Clear Sky Radiation Properties dataset;

(3)

Training the clear and cloudy sky models. The inputs of the clear sky model include the solar zenith angle, viewing zenith angle, relative Azimuth angle, TOA shortwave broadband albedo, reflectance (from channel 1 and 2) of AVHRR, and the brightness temperature (from channel 4 and 5) of AVHRR. The input of the cloudy sky model used the same input variables as the clear sky model and cloud optical depth;

(4)

Configuring the model coefficients. The optimal parameterization scheme was determined by looping in each parameter threshold.

Table 2. Parameters setting to determine the optimal parameters for the GBRT model.

Parameters	Threshold	Intervals
The number of iterations	50–300	50
Shrinkage	0.1–1	0.3
The depth of the tree	6–9	1
Sampling rate	0.2–1	0.2

shows the parameter setting details to determine the optimal parameterization for both the clear sky and cloudy sky conditions through the evaluation results (highest R² value and lowest bias and RMSE values) of the testing dataset for each loop;

(5)

Evaluating against the ground measurements.

Figure 3 shows the flowchart of the proposed GBRT model used in this study.

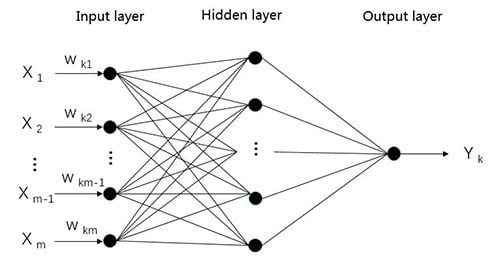
2.2.2. Artificial Neural Networks

ANNs are used as an empirical statistical method in a variety of applications such as classification, pattern recognition, forecasting, optimization, etc. [71,72,73]. An ANN model can be any model in which the output variables are computed from the input variables using compositions or connections of basic functions. In this research, a feedforward backpropagation neural network consisting of several layers of neurons was used. A neuron is a simplified mathematical model of a biological neuron, and a connection is a unique information transport link from a sending to a receiving neuron. Figure 4 shows a structural diagram of the ANN used in this study. The ANN model used here consists of three layers of neurons: input layers, hidden layers, and an output layer. Input ${\{x_j\}}_{j=1}^m$ is transmitted through a connection that multiplies its strength by a weight represented by ${\{w_{ij}\}}_{i=1}^k$. This gives the value x_iW_ij, which is an argument to a transfer function f that yields an output y_i.

$$y_i=f({\displaystyle \sum _{j=1}^m}{w}_{ij}{x}_j)$$

(2)

where i is the index of neuron in the hidden layer and j is the index of inputs to the neural network. A typical feedforward network trained with a resilient backpropagation algorithm [74,75] is employed to estimate DSR in this paper.

2.3. Constructing the Model

According to the characteristic variables in Table 1, corresponding data was extracted to establish the training dataset. Daily observed data from the CMA Meteorological Information Center from 2001 and 2002 were used as the response values (true values) of the training dataset. Information from the AVHRR cloudy and clear sky pixel detection was used to divide the training dataset into a cloudy sky training dataset and a clear sky training dataset. In addition, the missing values were removed both from the training and validation dataset.

2.3.1. Constructing the GBRT-Based DSR Model

The key step in building an efficient GBRT model is finding the optimal architecture. Building the GBRT model in a stage-wise fashion and regenerating the model minimizes the expected value of a certain loss function. After adding many trees to the model, the fitted model should have a small training error. However, it is important to remember that the generalization ability does not improve in direct proportion with the size of the fitted model; if the model is overfitted and possesses an extremely small error with the training dataset, its generalization ability will be poor. The performance of the GBRT model is influence by these four parameters as follows: the number of iterations, shrinkage, the depth of the tree, and the sampling rate [63]. As the number of iterations increases, model complexity will also increase, leading to poor prediction performance on the test dataset. Determining the appropriate number of iterations is essential to minimize future risks in prediction. Overfitting can be avoided by limiting the number of iterations and reducing the contribution of each tree. This is also known as shrinkage (or learning rate). There is a tradeoff between the number of iterations and the learning rate. A lower learning rate value means that the model is more robust but has a slower computing speed. The size of each tree is called the depth of the tree. The depth of the tree refers to the number of nodes in a tree. This parameter depends on the number of data points and the characteristic variables of the data. In theory, if the value of this parameter is too large, the model will run at a slower rate. The sampling rate is the ratio of the subsample to the total number of training instances. When set to 0.5, it means that the model randomly collected half the data instances to grow trees. This will prevent overfitting. This procedure should be used with adjusting the learning rate and the number of iterations.

In the present case, successive performance testing showed that an architecture of 250 trees with a tree depth of 6, a sampling rate of 0.6, and a learning rate of 0.1 was optimal to estimate the DSR under clear sky conditions. These values are 250, 6, 0.8, and 0.1, respectively, under cloudy sky conditions.

Considering that cloud optical depth is related to DSR under cloudy sky conditions, the cloud optical depth was chosen as the input data for the cloudy sky model. This was different from the input data used for the clear sky model. Table 1 shows the input data of the GBRT-based DSR model under clear sky and cloudy sky conditions. The debugging procedure for key parameters such as the number of trees, the size of each tree, the learning rate, and the subsample ratio was described earlier.

2.3.2. Constructing the ANN-Based DSR Model

The ANN training databases in this study were the same as those used in the GBRT model. The architecture is mainly defined by the number of layers, the number of neurons in each layer, and the transition function associated with each neuron. As for other parameters (e.g., initial weighting), details of these will not be shown in this paper. In the present case, successive performance testing has shown that an architecture with one hidden layer is sufficient to estimate DSR. The number of nodes in the input layer was set to nine nodes, and the number of nodes in the output layer was set to one. After testing, the number of the nodes in the hidden layer was 12 under clear sky conditions and 14 under cloudy sky conditions. The transfer function of the hidden layer was a tan-sigmoid transfer function, and those of the other two layers were linear functions under both clear sky and cloudy sky conditions. Theoretically, various sets of functions such as step, linear, and no linear functions could be used as the transfer function of different layers. However, the tan-sigmoid (for the hidden layer) and linear (for the input and output layers) types were most commonly used in the literature [71].

3. Results and Analysis

The estimated daily and monthly mean DSR based on the GBRT method were not only evaluated against ground measurements but also compared with the evaluation results from those estimated from the ANN-based DSR model. Additionally, the estimated DSR values were also compared with current existing DSR products from the GEWEX-SRB and the MERRA. The validation results were shown in terms of bias, RMSE, and correlation coefficient (R²).

3.1. Validation with Ground Measurements

3.1.1. Validation at a Daily Time Scale

The ground measurements at the selected 96 stations collected from CMA in 2003 were compared to the grid points of the estimated DSR based on the GBRT method. The performance of the GBRT-based DSR clear sky model using the training dataset and the validation dataset is shown in Figure 5. As shown in Figure 5, the daily estimated DSR correlates well with ground measurements under clear sky conditions. The daily DSR estimates under the clear sky conditions for the training dataset have an overall RMSE value of 19.05 W·m⁻² (19.06%), a bias value of 0.00 W·m⁻² (2.41%), and an R² value of 0.92. These values were 27.71 W·m⁻² (38.38%), −2.53 W·m⁻² (1.37%), and 0.82, respectively, for the validation dataset. The validation results at a daily time scale demonstrate that the GBRT is a practically applicable and effective method for estimating DSR under clear sky conditions using satellite observations from AVHRR data.

Figure 6 presents the evaluation results of the GBRT-based DSR cloudy sky model using the training dataset and the validation dataset. The daily DSR estimates for the training dataset under the cloudy sky conditions have an overall RMSE value of 33.37 W·m⁻² (30.21%), an R² value of 0.79, and a bias value of 0.01 W·m⁻² (4.74%). These values for the validation dataset were 42.97 W·m⁻² (34.57%), 0.64, and −2.83 W·m⁻² (1.45%), respectively. The accuracy was slightly lower than that of the clear sky model, which may be related to the influence of clouds [76].

When building the models for DSR estimation, we found that channel 4 and 5 influence the model accuracy. Figure 7 and Figure 8 show a comparison of the evaluation results without considering AVHRR channels 4 and 5 under clear and cloudy sky conditions, respectively. As shown in Figure 7, the daily DSR estimates without considering these two channels under clear sky conditions of the training dataset have an overall RMSE value of 26.52 W·m⁻² (23.93%), a bias value of −0.26 W·m⁻² (3.25%), and an R² value of 0.85. It can be concluded that the clear sky model yields higher accuracy if AVHRR channels 4 and 5 are considered. Similar results were also found under cloudy sky conditions. The daily DSR estimates without considering these two channels under cloudy sky conditions of the training dataset have an overall RMSE value of 37.52 W·m⁻² (31.86%), a bias value of 0.16 W·m⁻² (4.66%), and an R² value of 0.73. A potential reason for this may be the total atmospheric water vapor effect on DSR estimation, which may be to cause large uncertainties. Previous studies showed that AVHRR channels 4 and 5 have been widely used to retrieve the total atmospheric water vapor [77,78].

3.1.2. Validation at a Monthly Time Scale

To further show the relative accuracy of the GBRT method, we also validated the estimated DSR at a monthly time scale. To perform the comparison, monthly DSR estimates were obtained by averaging the daily DSR data of each month. Figure 9 shows the evaluation results of the training dataset and validation dataset based on the GBRT model of 2003 at a monthly time scale. The monthly estimated DSR of the training dataset has an overall RMSE value of 14.22 W·m⁻² (12.50%), a bias value of −0.30 W·m⁻² (2.04%), and an R² value of 0.94. These values were 15.40 W·m⁻² (12.93%), −2.25 W·m⁻² (1.01%), and 0.92, respectively, for the validation dataset. Like the validation results at a daily time scale, the validation results at a monthly time scale showed that the GBRT model is reasonably accurate.

3.2. Comparison with the ANN-Based Method

3.2.1. Validation at a Daily Time Scale

Figure 10a,b shows the evaluation results of the estimated daily DSR of the training and the validation dataset based on the ANN-based DSR model under clear sky and cloudy sky conditions. The daily DSR estimates based on the ANN-based clear sky model of the training dataset have an overall RMSE value of 26.53 W·m⁻² (41.84%) and a bias value of −0.09 W·m⁻² (0%). These values were 27.15 W·m⁻² (46.07%) and −3.67 W·m⁻² (1.60%), respectively, for the validation dataset. Although the RMSE of the estimated daily DSR of the validation dataset was slightly lower than that of the GBRT model, the mean absolute bias of the ANN-based model was 3.67 W·m⁻² (1.60%), which is larger than that of the GBRT model (2.53 W·m⁻² (1.37%)) (

Table 3. Comparison of the results of the ANN and GBRT models at a daily time scale (using measurements from 2001 and 2002 as the training dataset and measurements from 2003 as the validation dataset). The number in the parentheses is the percent bias or RMSE value.

Sky Condition	Dataset	Method	R2	RMSE (W·m−2)	Bias (W·m−2)
Clear sky	Training set	GBRT	0.92	19.05 (19.06%)	0 (2.41%)
		ANN	0.85	26.53 (41.84%)	−0.09 (0%)
	Validation set	GBRT	0.82	27.71 (38.38%)	−2.53 (1.37%)
		ANN	0.83	27.15 (46.07%)	−3.67 (1.60%)
Cloudy sky	Training set	GBRT	0.79	33.37 (30.21%)	0.01 (4.74%)
		ANN	0.66	42.07 (33.99%)	0.17 (3.13%)
	Validation set	GBRT	0.64	42.97 (34.57%)	−2.83 (1.45%)
		ANN	0.65	42.39 (34.50%)	−4.35 (0.17%)

). The evaluation results of the ANN-based cloudy sky model are shown in Figure 11. The daily DSR estimates based on the training dataset’s ANN cloudy sky DSR model have an overall RMSE value of 42.07 W·m⁻² (33.99%) and a bias value of 0.17 W·m⁻² (3.13%). These values were 42.39 W·m⁻² (34.50%) and −4.35 W·m⁻² (0.17%), respectively, for the validation dataset. According to the comparison results shown in Figure 10 and Figure 11 and Table 3, it was clear that the predictive abilities of the GBRT model are better than the ANN model at a daily time scale.

3.2.2. Validation at a Monthly Time Scale

Similar to what we did with the GBRT model, we also validated the estimated DSR at a monthly time scale to further show the accuracy of the ANN method. To perform the comparison, monthly DSR estimates were calculated by averaging the daily DSR of each month. Figure 12a shows the evaluation results of the training dataset based on the ANN-based DSR model in 2003 at a monthly time scale. The R² was 0.88, which was lower than that of GBRT model. The RMSE was 18.95 W·m⁻² (15.81%) larger than that of GBRT model. The evaluation results of the validation dataset’s monthly estimated DSR based on the ANN-based DSR model is shown in Figure 12b. The R² was 0.87, and the RMSE was 20.05 W·m⁻² (16.20%). As in the evaluation results at a daily time scale, it is obvious that the GBRT model performs better than the ANN model at a monthly time scale.

Although the DSR estimates based on the GBRT model at both daily and monthly time scales were relatively higher accuracy than those from the ANN-based model, the machine learning methods including GBRT and ANN are sensitive to the choice of parameters. Therefore, the parameters chosen for these two machine learning methods may influence the accuracy of the DSR estimates. In this study, the optimal parameterization scheme was determined by looping in each parameter threshold. Advanced methods for deriving the optimal parameters for both GBRT and ANN should be tested in the future.

3.3. Comparison with Existing DSR Products

3.3.1. Mapping DSR over China

To demonstrate the applicability of the GBRT-based DSR model for regional mapping, the surface monthly mean DSR was estimated based on the GBRT method in the mainland of China in March 2003. Figure 13a shows the estimated results for monthly DSR in March 2003. The GEWEX-SRB and MERRA monthly DSR for the same month are also shown in Figure 13b,c for comparison. According to these three figures, it can be concluded that the spatial distribution of estimated DSR based on the GBRT method is similar to that from the GEWEX-SRB. However, large discrepancies occurred in the comparison with the MERRA. Moreover, the DSR estimates from the GBRT model provide more details compared to the other two existing DSR products.

Figure 13d,e shows the differences between the monthly mean DSR estimates from the GBRT model and those from the GEWEX-SRB and the MERRA, respectively. Before comparison, the DSR estimates from the GBRT model and the MERRA were projected onto a 1° spatial resolution using bilinear interpolation to match the resolution of the GEWEX-SRB data. As shown in the Figure 13, the differences between the GBRT-based DSR estimates and the GEWEX-SRB DSR product were smaller than that between the GBRT-based DSR estimates and the MERRA DSR product. The maximum differences between the GBRT-based DSR estimates and the GEWEX-SRB DSR product were found in the Tibetan Plateau. The maximum differences between the GBRT-based DSR estimates and the MERRA DSR product were found in southeast China, which were greater than 100 W·m⁻² at some areas. The large discrepancies in the Tibetan Plateau may be related to the high elevation of the area. Yang et al. [32] pointed out that the discrepancies among the satellite products were always larger in highly variable terrain and smaller for non-variable terrain. The large differences in southeast China were probably due to inappropriate representation of aerosols and clouds, as well as their interactions with the algorithms used for this region [79,80]. In this area, heavy pollution is occurring due to rapid economic development and high population density. However, the DSR comparison of the GBRT model and current existing products were only performed for one month. This may also cause large uncertainties. Therefore, further investigations should be conducted for DSR estimation in the future if long-term DSR estimates are generated based on the GBRT method.

3.3.2. Validation with Ground Measurements

To further show the accuracy of the DSR estimates based on the GBRT method, we also compared the evaluation results of the GBRT-based daily estimated DSR against ground measurements from CMA in 2003 with those of current existing DSR products from the GEWEX-SRB and the MERRA. As shown in Figure 14, the daily estimated DSR based on the GBRT method correlates very well with the ground measurements, with an RMSE value of 31.65 W·m⁻² (21.34%) and a bias value of 0.86 W·m⁻² (1.50%). These values were 40.82 W·m⁻² (30.93%) and 27.39 W·m⁻² (17.86%), respectively, for the GEWEX-SRB-based estimates, and 74.2 W·m⁻² (39.40%) and 57.27 W·m⁻² (30.06%), respectively, for the MERRA-based estimates. It was obvious that the evaluation results of the GBRT-based DSR model were better than those of the other two products. However, the spatial representativeness of ground measurements is a potential error source for DSR evaluation.

As pointed out by Hakuba et al. [81], the monthly and annual mean representation error at the surface sites with respect to their 1° surroundings are, on average, 3.7% (4 W·m⁻²) and 2% (3 W·m⁻²), respectively. The DSR estimates from the GBRT model and current existing radiation products have different spatial resolutions. Therefore, the regional dependence of errors of coarse-resolution satellite products for complex terrain may cause large discrepancies.

4. Conclusions

DSR is an essential parameter in the terrestrial radiation budget and a necessary input for land-surface process models. Although several radiation products using satellite observations have been released, their coarse spatial resolution and low accuracy limit their application. Therefore, high spatio-temporal resolution and high accuracy DSR is still required for many applications. To achieve this goal, a fast, accurate, and robust GBRT method that has the ability to handle different types of input variables and model complex relations was developed to estimate DSR using satellite observations from AVHRR.

The estimated DSR was evaluated using the ground measurements from CMA and was compared with one remote sensing DSR product (the GEWEX-SRB) and one reanalysis DSR product (the MERRA). The daily estimated DSR had an overall R² value of 0.82, an RMSE of 27.71 W·m⁻² (38.38%), and a bias of −2.53 W·m⁻² (1.37%) under clear sky conditions, and an R² of 0.64, an RMSE of 42.97 W·m⁻² (34.57%), and a bias of −2.83 W·m⁻² (1.45%) under cloudy sky conditions. Comparison of the DSR estimates with the reanalyzed and the retrieved DSR values from satellite observation showed that the estimated DSR values are reasonably accurate but with higher spatial resolution. However, the DSR comparison of the GBRT model and current existing products was only performed for one month, which may cause large uncertainties. Beside this, measurement errors (e.g., instrument sensitivity, drift, and urbanization effects) and spatial representativeness of surface measurements are potential sources of error in DSR estimation [81]. Therefore, further investigations should be conducted for DSR estimation in the future if long-term DSR estimates are generated based on the GBRT method.

The strengths of GBRT are accuracy, speed, and robustness [51]. To show the advantages of GBRT, an ANN model was built. The results were compared between the GBRT-based DSR model and the ANN-based DSR model under clear and cloudy sky conditions, as shown in Section 3.2. The daily validation analysis showed that the maximum RMSE for GBRT-based and ANN-based clear sky model was less than 28 W·m⁻², but the bias of the GBRT-based clear sky model (−2.53 W·m⁻²) was less than that of the ANN-based clear sky model (−3.67 W·m⁻²). Similar results were also found for the cloudy sky model. The ANN has two known disadvantages: it needs a relatively long processing time to train a model with many input variables, and it behaves unpredictably when overestimation occurs during the training stage [82]. In contrast, the GBRT was evaluated as a promising machine learning approach in terms of processing speed and accuracy. All experiments were conducted on a Windows 7 Intel(R) Core(TM) i7-6700 CPU, 3.4 GHz, 20.00 GB RAM processor. The means for the elapsed time of completion of the GBRT clear sky model and the GBRT cloudy sky model were within 10 seconds. Therefore, we conclude that the GBRT method performs better than the ANN method for DSR estimation in this study. As it is well known, the mechanisms of machine learning methods are often considered to be black boxes, and the training procedure is sensitive to the choice of parameters. These limitations may influence the accuracy of the DSR estimates.

The contributions of this study demonstrate that the GBRT is efficient and practical for estimating DSR using remote sensing and ground observation data. Simultaneously, this method has a very good development procedure for defining training data and generating parameters. The method also has more extensive applicability than other current methods. The proposed GBRT-based method can also be used for the retrieval of other land surface variables.