Interferometric SAR DEMs for Forest Change in Uganda 2000–2012
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. SRTM Data
2.3. TanDEM-X Data
2.4. Estimating the X-C Penetration Difference
2.5. Estimating Height Changes Over Time
2.6. Vertical Bias Adjustment
2.7. Estimating AGB and Carbon Change
2.8. Estimation of Uncertainty and Summary Statistics
2.9. Comparison and Validation with External Data Sets
3. Results and Discussion
3.1. Estimating the X-C Penetration Difference
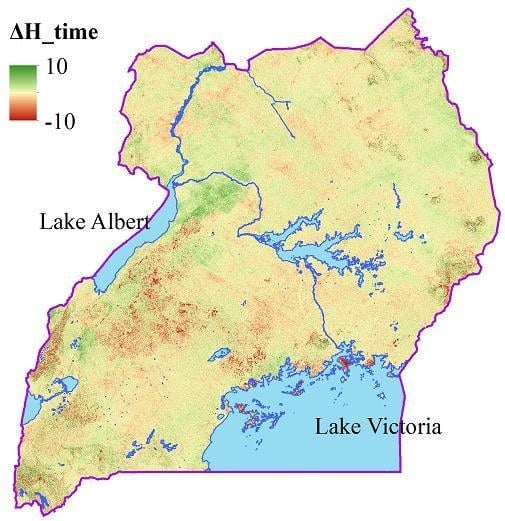
3.2. Estimating Height Changes Over Time
3.3. Vertical Bias Adjustment
3.4. Summary Statistics and Uncertainty
3.5. Comparison and Validation with External Datasets
4. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Ciais, P.; Sabine, C.; Bala, G.; Bopp, L.; Brovkin, V.; Canadell, J.; Chhabra, A.; DeFries, R.; Galloway, J.; Heimann, M.; et al. Carbon and Other Biogeochemical Cycles. In Climate Change 2013: The Physical Science Basis; Stocker, T.F., Qin, D., Plattner, G.-K., Tignor, M., Allen, S.K., Boschung, J., Nauels, A., Xia, Y., Bex, V., Midgley, P.M., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2013. [Google Scholar]
- Intergovernmental Panel on Climate Change (IPCC). Climate Change 2014: Mitigation of Climate Change: IPCC Working Group III Contribution to the Fifth Assesment Report of the Intergovernmental Panel on Climate Change; Edenhofer, O., Pichs-Madruga, R., Sokona, Y., Farahani, E., Kadner, S., Seyboth, K., Adler, A., Baum, I., Brunner, S., Eickemeier, P., et al., Eds.; Cambridge University Press: Cambridge, UK; New York, NY, USA, 2014. [Google Scholar]
- UNFCCC. Decision 2/Cp. 13: Reducing Emissions from Deforestation in Developing Countries: Approaches to Stimulate Action; United Nations Framework Convention on Climate Chgange: Bonn, Germany, 2007; Available online: http://Unfccc.Int/Resource/Docs/2007/Cop13/Eng/06a01.Pdf (accessed on 19 September 2014).
- Decision 4/Cp.15. Methodological Guidance for Activities Relating to Reducing Emissions from Deforestation and Forest Degradation and the Role of Conservation, Sustainable Management of Forests and Enhancement of Forest Carbon Stocks in Developing Countries; United Nations Framework Convention on Climate Change: Bonn, Germany, 2009; Available online: http://Unfccc.Int/Resource/Docs/2009/Cop15/Eng/11a01.Pdf (accessed on 19 September 2014).
- Quéré, C.L.; Moriarty, R.; Andrew, R.M.; Canadell, J.G.; Sitch, S.; Korsbakken, J.I.; Friedlingstein, P.; Peters, G.P.; Andres, R.J.; Boden, T.A.; et al. Global Carbon Budget 2015. Earth Syst. Sci. Data 2015, 7, 349–396. [Google Scholar] [CrossRef] [Green Version]
- Houghton, R.A.; House, J.I.; Pongratz, J.; Van Der Werf, G.R.; DeFries, R.S.; Hansen, M.C.; Quere, C.L.; Ramankutty, N. Carbon Emissions from Land Use and Land-Cover Change. Biogeosciences 2012, 9, 5125–5142. [Google Scholar] [CrossRef]
- MacDicken, K.G. Global Forest Resources Assessment 2015: What, Why and How? For. Ecol. Manag. 2015, 352, 3–8. [Google Scholar] [CrossRef]
- Pan, Y.D.; Birdsey, R.A.; Fang, J.Y.; Houghton, R.; Kauppi, P.E.; Kurz, W.A.; Phillips, O.L.; Shvidenko, A.; Lewis, S.L.; Canadell, J.G.; et al. A Large and Persistent Carbon Sink in the World’s Forests. Science 2011, 333, 988–993. [Google Scholar] [CrossRef] [PubMed]
- Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; Kommareddy, A.; et al. High-Resolution Global Maps of 21st-Century Forest Cover Change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [PubMed]
- Hansen, M.C.; Shimabukuro, Y.E.; Potapov, P.; Pittman, K. Comparing Annual MODIS and Prodes Forest Cover Change Data for Advancing Monitoring of Brazilian Forest Cover. Remote Sens. Environ. 2008, 112, 3784–3793. [Google Scholar] [CrossRef]
- Baccini, A.; Goetz, S.J.; Walker, W.S.; Laporte, N.T.; Sun, M.; Sulla-Menashe, D.; Hackler, J.; Beck, P.S.A.; Dubayah, R.; Friedl, M.A.; et al. Estimated Carbon Dioxide Emissions from Tropical Deforestation Improved by Carbon-Density Maps. Nat. Clim. Chang. 2012, 2, 182–185. [Google Scholar] [CrossRef]
- Saatchi, S.S.; Harris, N.L.; Brown, S.; Lefsky, M.; Mitchard, E.T.A.; Salas, W.; Zutta, B.R.; Buermann, W.; Lewis, S.L.; Hagen, S.; et al. Benchmark Map of Forest Carbon Stocks in Tropical Regions across Three Continents. Proc. Natl. Acad. Sci. USA 2011, 108, 9899–9904. [Google Scholar] [CrossRef] [PubMed]
- Avitabile, V.; Baccini, A.; Friedl, M.A.; Schmullius, C. Capabilities and Limitations of Landsat and Land Cover Data for Aboveground Woody Biomass Estimation of Uganda. Remote Sens. Environ. 2012, 117, 366–380. [Google Scholar] [CrossRef]
- Mitchard, E.T.A.; Feldpausch, T.R.; Brienen, R.J.W.; Lopez-Gonzalez, G.; Monteagudo, A.; Baker, T.R.; Lewis, S.L.; Lloyd, J.; Quesada, C.A.; Gloor, M.; et al. Markedly Divergent Estimates of Amazon Forest Carbon Density from Ground Plots and Satellites. Glob. Ecol. Biogeogr. 2014, 23, 935–946. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Avitabile, V.; Herold, M.; Henry, M.; Schmullius, C. Mapping Biomass with Remote Sensing: A Comparison of Methods for the Case Study of Uganda. Carbon Balance Manag. 2011, 6, 7. [Google Scholar] [CrossRef] [PubMed]
- Næsset, E. Predicting Forest Stand Characteristics with Airborne Scanning Laser Using a Practical Two-Stage Procedure and Field Data. Remote Sens. Environ. 2002, 80, 88–99. [Google Scholar] [CrossRef]
- Persson, H. Estimation of Boreal Forest Attributes from Very High Resolution Pléiades Data. Remote Sens. 2016, 8, 736. [Google Scholar] [CrossRef]
- Karjalainen, M.; Kankare, V.; Vastaranta, M.; Holopainen, M.; Hyyppa, J. Prediction of Plot-Level Forest Variables Using Terrasar-X Stereo Sar Data. Remote Sens. Environ. 2012, 117, 338–347. [Google Scholar] [CrossRef]
- Treuhaft, R.N.; Madsen, S.N.; Moghaddam, M.; Zyl, J.J. Vegetation Characteristics and Underlying Topography from Interferometric Radar. Radio Sci. 1996, 31, 1449–1485. [Google Scholar] [CrossRef]
- Treuhaft, R.N.; Siqueira, P.R. Vertical Structure of Vegetated Land Surfaces from Interferometric and Polarimetric Radar. Radio Sci. 2000, 35, 141–177. [Google Scholar] [CrossRef]
- Askne, J.I.H.; Dammert, P.B.G.; Ulander, L.M.H.; Smith, G. C-Band Repeat-Pass Interferometric Sar Observations of the Forest. IEEE Trans. Geosci. Remote Sens. 1997, 35, 25–35. [Google Scholar] [CrossRef]
- Soja, M.J.; Persson, H.; Ulander, L.M.H. Estimation of Forest Height and Canopy Density from a Single Insar Correlation Coefficient. IEEE Geosci. Remote Sens. Lett. 2015, 12, 646–650. [Google Scholar] [CrossRef]
- Soja, M.J.; Persson, H.J.; Ulander, L.M. Estimation of Forest Biomass from Two-Level Model Inversion of Single-Pass Insar Data. IEEE Trans. Geosci. Remote Sens. 2015, 53, 5083–5099. [Google Scholar] [CrossRef]
- Treuhaft, R.; Lei, Y.; Gonçalves, F.; Keller, M.; Santos, J.; Neumann, M.; Almeida, A. Tropical-Forest Structure and Biomass Dynamics from Tandem-X Radar Interferometry. Forests 2017, 8, 277. [Google Scholar] [CrossRef]
- Kellndorfer, J.; Walker, W.; Pierce, L.; Dobson, C.; Fites, J.A.; Hunsaker, C.; Vona, J.; Clutter, M. Vegetation Height Estimation from Shuttle Radar Topography Mission and National Elevation Datasets. Remote Sens. Environ. 2004, 93, 339–358. [Google Scholar] [CrossRef]
- Kenyi, L.W.; Dubayah, R.; Hofton, M.; Schardt, M. Comparative Analysis of Srtm-Ned Vegetation Canopy Height to Lidar-Derived Vegetation Canopy Metrics. Int. J. Remote Sens. 2009, 30, 2797–2811. [Google Scholar] [CrossRef]
- Sexton, J.O.; Bax, T.; Siqueira, P.; Swenson, J.J.; Hensley, S. A Comparison of Lidar, Radar, and Field Measurements of Canopy Height in Pine and Hardwood Forests of Southeastern North America. For. Ecol. Manag. 2009, 257, 1136–1147. [Google Scholar] [CrossRef]
- Solberg, S.; Astrup, R.; Bollandsas, O.M.; Naesset, E.; Weydahl, D.J. Deriving Forest Monitoring Variables from X-Band Insar Srtm Height. Can. J. Remote Sens. 2010, 36, 68–79. [Google Scholar] [CrossRef]
- Ni, W.; Guo, Z.; Sun, G.; Chi, H. Investigation of Forest Height Retrieval Using Srtm-Dem and Aster-Gdem. Presented at the International Geoscience and Remote Sensing Symposium (IGARSS), Honolulu, HI, USA, 25–30 July 2010. [Google Scholar]
- Solberg, S.; Astrup, R.; Breidenbach, J.; Nilsen, B.; Weydahl, D. Monitoring Spruce Volume and Biomass with Insar Data from Tandem-X. Remote Sens. Environ. 2013, 139, 60–67. [Google Scholar] [CrossRef]
- Solberg, S.; Astrup, R.; Weydahl, D.J. Detection of Forest Clear-Cuts with Shuttle Radar Topography Mission (Srtm) and Tandem-X Insar Data. Remote Sens. 2013, 5, 5449–5462. [Google Scholar] [CrossRef]
- Woodhouse, I.H. Predicting Backscatter-Biomass and Height-Biomass Trends Using a Macroecology Model. IEEE Trans. Geosci. Remote Sens. 2006, 44, 871–877. [Google Scholar] [CrossRef]
- Neeff, T.; Dutra, L.V.; Dos Santos, J.R.; Freitas, C.D.; Araujo, L.S. Tropical Forest Measurement by Interferometric Height Modeling and P-Band Radar Backscatter. For. Sci. 2005, 51, 585–594. [Google Scholar]
- Gama, F.F.; Dos Santos, J.R.; Mura, J.C. Eucalyptus Biomass and Volume Estimation Using Interferometric and Polarimetric Sar Data. Remote Sens. 2010, 2, 939–956. [Google Scholar] [CrossRef]
- Solberg, S.; Hansen, E.H.; Gobakken, T.; Næssset, E.; Zahabu, E. Biomass and Insar Height Relationship in a Dense Tropical Forest. Remote Sens. Environ. 2017, 192, 166–175. [Google Scholar] [CrossRef]
- Puliti, S.; Solberg, S.; Næsset, E.; Gobakken, T.; Zahabu, E.; Mauya, E.; Malimbwi, R.E. Modelling above Ground Biomass in Tanzanian Miombo Woodlands Using Tandem-X Worlddem and Field Data. Remote Sens. 2017, 9, 984. [Google Scholar] [CrossRef]
- Solberg, S.; Næsset, E.; Gobakken, T.; Bollandsås, O.M. Forest Biomass Change Estimated from Height Change in Interferometric Sar Height Models. Carbon Balance Manag. 2014, 9, 5. [Google Scholar] [CrossRef] [PubMed]
- Solberg, S.; Weydahl, D.J.; Astrup, R. Temporal Stability of X-Band Single-Pass Insar Heights in a Spruce Forest: Effects of Acquisition Properties and Season. IEEE Trans. Geosci. Remote Sens. 2015, 53, 1607–1614. [Google Scholar] [CrossRef]
- Solberg, S.; Lohne, T.P.; Karyanto, O. Temporal Stability of Insar Height in a Tropical Rainforest. Remote Sens. Lett. 2015, 6, 209–217. [Google Scholar] [CrossRef]
- Praks, J.; Demirpolat, C.; Antropov, O.; Hallikainen, M. On Forest Height Retrival from Spaceborne X-Band Inferometic Sar Images under Variable Seasonal Conditions. In Proceedings of the XXXII Finnish URSI Convention on Radio Science and SMARAD Seminar, Otaniemi, Finland, 24–25 April 2013; pp. 115–118. [Google Scholar]
- Way, J.; Paris, J.; Kasischke, E.; Slaughter, C.; Viereck, L.; Christensen, N.; Dobson, M.C.; Ulaby, F.; Richards, J.; Milne, A.; et al. The Effect of Changing Environmental-Conditions on Microwave Signatures of Forest Ecosystems: Preliminary Results of the March 1988 Alaskan Aircraft Sar Experiment. Int. J. Remote Sens. 1990, 11, 1119–1144. [Google Scholar] [CrossRef]
- Hoffmann, J.; Walter, D. How Complementary Are Srtm-X and -C Band Digital Elevation Models? Photogramm. Eng. Remote Sens. 2006, 72, 261–268. [Google Scholar] [CrossRef]
- Walker, W.S.; Kellndorfer, J.M.; Pierce, L.E. Quality Assessment of Srtm C- and X-Band Interferometric Data: Implications for the Retrieval of Vegetation Canopy Height. Remote Sens. Environ. 2007, 106, 428–448. [Google Scholar] [CrossRef]
- Drichi, P. National Biomass Study Technical Report 1996–2002; Kampala, Forest Department, Ministry of Water, Lands and Environment: Kampala, Uganda, 2002.
- MoWE. Proposed Forest Reference Level for Uganda; Republic of Uganda Ministry of Water and Environment: Kampala, Uganda, 2017. Available online: http://Redd.Unfccc.Int/Files/Uganda_Frel_Final_Version_16.01.Pdf (accessed on 23 August 2017).
- Rabus, B.; Eineder, M.; Roth, A.; Bamler, R. The Shuttle Radar Topography Mission—A New Class of Digital Elevation Models Acquired by Spaceborne Radar. ISPRS J. Photogramm. Remote Sens. 2003, 57, 241–262. [Google Scholar] [CrossRef]
- Krieger, G.; Moreira, A.; Fiedler, H.; Hajnsek, I.; Werner, M.; Younis, M.; Zink, M. Tandem-X: A Satellite Formation for High-Resolution Sar Interferometry. IEEE Trans. Geosci. Remote Sens. 2007, 45, 3317–3341. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Shi, P.; Deng, L.; Li, J. Generation of a Top-of-Canopy Digital Elevation Model (DEM) in Tropical Rain Forest Regions Using Radargrammetry. Int. J. Remote Sens. 2007, 28, 4345–4349. [Google Scholar] [CrossRef]
- Intergovernmental Panel on Climate Change (IPCC). Guidelines for National Greenhouse Gas Inventories: Volume 4: Agriculture, Forestry and Other Land Use; Institute for Global Environmental Strategies: Kanagawa Prefecture, Japan, 2006. [Google Scholar]
- Friedl, M.A.; Sulla-Menashe, D.; Tan, B.; Schneider, A.; Ramankutty, N.; Sibley, A.; Huang, X. MODIS Collection 5 Global Land Cover: Algorithm Refinements and Characterization of New Datasets, 2001–2012; Collection 5.1 Igbp Land Cover; Boston University: Boston, MA, USA, 2010. [Google Scholar]









| Source | DF | Sum of Squares | Mean Square |
|---|---|---|---|
| Artifact lines, Lm | 1966 | 678,972,490 | 345,357 |
| ΔH_penetration | 10 | 1,553,541 | 155,354 |
| Error, e1 | 68,309,116 | 540,543,128 | 8 |
| Corrected Total | 68,311,092 | 1,221,069,159 |
| Source | DF | Sum of Squares | Mean Square |
|---|---|---|---|
| Artifact lines, L1i | 756 | 16,031,767 | 21,206 |
| Artifact lines, L2j | 534 | 17,213,609 | 32,235 |
| Artifact bands, B1k | 3 | 46,665,641 | 15,555,214 |
| Artifact bands, B2l | 3 | 2,378,282 | 792,761 |
| Error, e2 | 76,153,436 | 361,137,038 | 5 |
| Corrected Total | 76,154,732 | 443,426,337 |
| Source | Mean | SE | Lower 95% CI | Upper 95% CI |
|---|---|---|---|---|
| ΔH_time | −0.073 | 0.022 | −0.116 | −0.030 |
| ΔAGB | −1.26 | 0.27 | −1.79 | −0.73 |
| Parameter | N | Mean | Min | Max | SE_mean | SE_min | SE_max |
|---|---|---|---|---|---|---|---|
| Penetration XC | 11 | −0.368 | −0.799 | 0.205 | 0.00354 | 0.00000 | 0.00522 |
| Intercept | 1 | 0.00513 | - | - | 0.208 | - | - |
| L1 | 757 | 0.437 | −0.897 | 1.710 | 0.0607 | 0.0000 | 0.0921 |
| L2 | 535 | −1.61 | −3.92 | 0.500 | 0.200 | 0.000 | 0.659 |
| B1 | 4 | −0.921 | −1.32 | 0.000 | 0.00162 | 0.00000 | 0.00348 |
| B2 | 4 | 0.541 | 0.000 | 1.22 | 0.00204 | 0.00000 | 0.00349 |
| AGB | 2 | 11.90 | 18.40 | 24.1 | 203 |
| No. | MODIS Land Cover Type | ΔH_Time, m | ΔAGB, t/ha | ||||
|---|---|---|---|---|---|---|---|
| Loss | No Change | Gain | Loss | No Change | Gain | ||
| 2 | Evergreen broadleaf forest | −8.5 | −0.7 | 1.0 | −156.3 | −12.9 | 18.0 |
| 8 | Woody savanna | −3.3 | 0.4 | 1.2 | −39.3 | 4.8 | 13.8 |
| 9 | Savanna | −1.3 | −0.1 | 1.9 | −15.0 | −0.9 | 22.1 |
| 10 | Grassland | −1.5 | 0.3 | 0.2 | −18.4 | 3.7 | 2.8 |
| 11 | Permanent wetlands | −3.0 | 0.5 | 0.6 | −36.0 | 6.5 | 7.0 |
| 12 | Croplands | −1.2 | 0.2 | 1.4 | −14.3 | 2.9 | 16.3 |
| 14 | Cropland and natural vegetation mosaic | −3.6 | −0.1 | 1.5 | −42.6 | −1.3 | 17.3 |
| Others | −3.7 | 0.7 | 1.5 | −44.5 | 8.3 | 17.7 | |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Solberg, S.; May, J.; Bogren, W.; Breidenbach, J.; Torp, T.; Gizachew, B. Interferometric SAR DEMs for Forest Change in Uganda 2000–2012. Remote Sens. 2018, 10, 228. https://doi.org/10.3390/rs10020228
Solberg S, May J, Bogren W, Breidenbach J, Torp T, Gizachew B. Interferometric SAR DEMs for Forest Change in Uganda 2000–2012. Remote Sensing. 2018; 10(2):228. https://doi.org/10.3390/rs10020228
Chicago/Turabian StyleSolberg, Svein, Johannes May, Wiley Bogren, Johannes Breidenbach, Torfinn Torp, and Belachew Gizachew. 2018. "Interferometric SAR DEMs for Forest Change in Uganda 2000–2012" Remote Sensing 10, no. 2: 228. https://doi.org/10.3390/rs10020228
APA StyleSolberg, S., May, J., Bogren, W., Breidenbach, J., Torp, T., & Gizachew, B. (2018). Interferometric SAR DEMs for Forest Change in Uganda 2000–2012. Remote Sensing, 10(2), 228. https://doi.org/10.3390/rs10020228