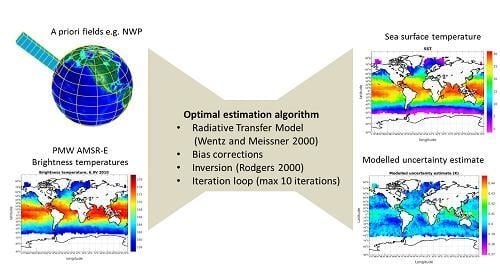
Optimal Estimation of Sea Surface Temperature from AMSR-E
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
2.1.1. AMSR-E Brightness Temperatures
2.1.2. In Situ Observations
2.1.3. Ancillary Data Fields
2.2. Matchup Database
2.2.1. ESA-CCI Multi-Sensor Matchup Dataset
2.2.2. Data Filtering Methods
2.3. Optimal Estimation Development
2.3.1. Initial OE Setup
2.3.2. Testing for Convergence
2.3.3. Improving the Forward Model
3. Results
3.1. SST Sensitivity
3.2. Retrieval Uncertainty
3.3. Validation against Independent Argo Floats
3.4. OE vs. NWP Latitudinal Performance
4. Discussion
5. Conclusions
- That the future 6–7 GHz frequency wide swath imaging capability currently provided by GCOM-W AMSR-2 is sustained by flying a new mission. This implies immediate initiation of satellite development for a potential launch in 2025.
- That the spatial resolution of the 6–7 GHz frequency channels is significantly improved to provide a ~10 km native instantaneous spatial resolution (which may imply using a large 6–9 m rotating deployable mesh antenna). This is required to minimize significant loss of data in the coastal zone and marginal sea ice zone due to side lobe contamination, currently there are no valid measurements within 100 km of these areas.
- That the radiometric quality of future satellite microwave radiometers is significantly improved over current capability. This is required because in many areas imaging microwave radiometer measurements are the only measurements available for the SST climate data record in areas characterized by quasi-permanent cloud cover that confounds thermal IR satellite SST retrievals.
- That appropriate combination with one or more higher-frequency channels (10, 18, 37 GHz) is provided in order to resolve the ambiguities in the microwave measurements if too few channels are available.
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Vázquez-Cuervo, J.; Armstrong, E.M.; Harris, A. The effect of aerosols and clouds on the retrieval of infrared sea surface temperatures. J. Clim. 2004, 17, 3921–3933. [Google Scholar] [CrossRef]
- Reynolds, R.W. Impact of mount pinatubo aerosols on satellite-derived sea surface temperatures. J. Clim. 1993, 6, 768–774. [Google Scholar] [CrossRef]
- Reynolds, R.W.; Rayner, N.A.; Smith, T.M.; Stokes, D.C.; Wang, W. An improved in situ and satellite sst analysis for climate. J. Clim. 2002, 15, 1609–1625. [Google Scholar] [CrossRef]
- Donlon, C.; Rayner, N.; Robinson, I.; Poulter, D.J.S.; Casey, K.S.; Vazquez-Cuervo, J.; Armstrong, E.; Bingham, A.; Arino, O.; Gentemann, C.; et al. The global ocean data assimilation experiment high-resolution sea surface temperature pilot project. Bull. Am. Meteorol. Soc. 2007, 88, 1197–1213. [Google Scholar] [CrossRef]
- Donlon, C.J.; Casey, K.S.; Gentemann, C.L.; Harris, A. Successes and challenges for the modern sea surface temperature observing system. In Proceeding of OceanObs’09: Sustained Ocean Observations and Information for Society; Hall, J., Harrison, D.E., Stammer, D., Eds.; ESA Publication WPP-306: Venice, Italy, 2010; Volume 2. [Google Scholar]
- Wentz, F.J.; Gentemann, C.; Smith, D.; Chelton, D.B. Satellite measurements of sea surface temperature through clouds. Science 2000, 288, 847–850. [Google Scholar] [CrossRef] [PubMed]
- Chelton, D.B.; Wentz, F.J. Global microwave satellite observations of sea surface temperature for numerical weather prediction and climate research. Bull. Am. Meteorol. Soc. 2005, 86, 1097–1115. [Google Scholar] [CrossRef]
- Wilheit, T.T.; Chang, A.T.C. An algorithm for retrieval of ocean surface and atmospheric parameters from the observations of the scanning multichannel microwave radiometer. Radio Sci. 1980, 15, 525–544. [Google Scholar] [CrossRef]
- Lipes, R.G. Description of SEASAT radiometer status and results. J. Geophys. Res. 1982, 87. [Google Scholar] [CrossRef]
- Milman, A.S.; Wilheit, T.T. Sea surface temperatures from the scanning multichannel microwave radiometer on Nimbus 7. J. Geophys. Res. 1985, 90. [Google Scholar] [CrossRef]
- Maeda, T.; Taniguchi, Y.; Imaoka, K. GCOM-W1 AMSR2 Level 1R Product: Dataset of brightness temperature modified using the antenna pattern matching technique. IEEE Trans. Geosci. Remote Sens. 2016, 54, 770–782. [Google Scholar] [CrossRef]
- Gaiser, P.W.; St Germain, K.M.; Twarog, E.M.; Poe, G.A.; Purdy, W.; Richardson, D.; Grossman, W.; Jones, W.L.; Spencer, D.; Golba, G.; et al. The WindSat spaceborne polarimetric microwave radiometer: Sensor description and early orbit performance. IEEE Trans. Geosci. Remote Sens. 2004, 42, 2347–2361. [Google Scholar] [CrossRef]
- Xie, S.-P. Satellite observations of cool ocean—Atmosphere interaction*. Bull. Am. Meteorol. Soc. 2004, 85, 195–208. [Google Scholar] [CrossRef]
- Shibata, A. Calibration of AMSR-E SST toward a monitoring of global warming. In Proceedings of the 2005 IEEE International Geoscience and Remote Sensing Symposium, Seoul, Korea, 29 July 2005. [Google Scholar]
- Shibata, A. Features of ocean microwave emission changed by wind at 6 GHz. J. Oceanogr. 2006, 62, 321–330. [Google Scholar] [CrossRef]
- Wentz, F.J.; Meissner, T. AMSR_E Ocean Algorithms; Remote Sensing Systems: Santa Rosa, CA, USA, 2007; p. 6. [Google Scholar]
- Hosoda, K.; Murakami, H.; Shibata, A.; Sakaida, F.; Kawamura, H. Difference characteristics of sea surface temperature observed by GLI and AMSR aboard ADEOS-II. J. Oceanogr. 2006, 62, 339–350. [Google Scholar] [CrossRef]
- Gentemann, C.L. Three way validation of MODIS and AMSR-E sea surface temperatures. J. Geophys. Res. Oceans 2014, 119, 2583–2598. [Google Scholar] [CrossRef]
- Donlon, C.J.; Martin, M.; Stark, J.; Roberts-Jones, J.; Fiedler, E.; Wimmer, W. The Operational Sea Surface Temperature and Sea Ice Analysis (OSTIA) system. Remote Sens. Environ. 2012, 116, 140–158. [Google Scholar] [CrossRef]
- Hosoda, K.; Kawamura, H.; Sakaida, F. Improvement of New Generation Sea Surface Temperature for Open ocean (NGSST-O): A new sub-sampling method of blending microwave observations. J. Oceanogr. 2015, 71, 205–220. [Google Scholar] [CrossRef]
- Stark, J.D.; Donlon, C.J.; Martin, M.J.; McCulloch, M.E. OSTIA : An operational, high resolution, real time, global sea surface temperature analysis system. In Proceedings of the OCEANS, Aberdeen, UK, 18–21 June 2007; pp. 1–4. [Google Scholar]
- Reynolds, R.W.; Smith, T.M.; Liu, C.; Chelton, D.B.; Casey, K.S.; Schlax, M.G. Daily high-resolution-blended analyses for sea surface temperature. J. Clim. 2007, 20, 5473–5496. [Google Scholar] [CrossRef]
- Donlon, C.; Casey, K.; Robinson, I.; Gentemann, C.; Reynolds, R.; Barton, I.; Arino, O.; Stark, J.; Rayner, N.; LeBorgne, P.; et al. The GODAE high-resolution sea surface temperature pilot project. Oceanography 2009, 22, 34–45. [Google Scholar] [CrossRef]
- Merchant, C.J.; Le Borgne, P.; Marsouin, A.; Roquet, H. Optimal estimation of sea surface temperature from split-window observations. Remote Sens. Environ. 2008, 112, 2469–2484. [Google Scholar] [CrossRef]
- Merchant, C.J.; Le Borgne, P.; Roquet, H.; Marsouin, A. Sea surface temperature from a geostationary satellite by optimal estimation. Remote Sens. Environ. 2009, 113, 445–457. [Google Scholar] [CrossRef]
- Merchant, C.J.; Embury, O. Simulation and Inversion of Satellite Thermal Measurements. In Experimental Methods in the Physical Sciences; Elsevier: Amsterdam, The Netherlands, 2014; Volume 47, pp. 489–526. ISBN 978-0-12-417011-7. [Google Scholar]
- Merchant, C.J.; Embury, O.; Roberts-Jones, J.; Fiedler, E.; Bulgin, C.E.; Corlett, G.K.; Good, S.; McLaren, A.; Rayner, N.; Morak-Bozzo, S.; et al. Sea surface temperature datasets for climate applications from Phase 1 of the European Space Agency Climate Change Initiative (SST CCI). Geosci. Data J. 2014, 1, 179–191. [Google Scholar] [CrossRef]
- Merchant, C.J.; Le Borgne, P.; Roquet, H.; Legendre, G. Extended optimal estimation techniques for sea surface temperature from the Spinning Enhanced Visible and Infra-Red Imager (SEVIRI). Remote Sens. Environ. 2013, 131, 287–297. [Google Scholar] [CrossRef]
- Pedersen, L.T. Merging microwave radiometer data and meteorological data for improved sea ice concentrations. EARSeL Adv. Remote Sens. 1994, 3, 81–89. [Google Scholar]
- Melsheimer, C.; Heygster, G.; Mathew, N.; Toudal Pedersen, L. Retrieval of sea ice emissivity and integrated retrieval of surface and atmospheric parameters over the Arctic from AMSR-E data. J. Remote Sens. Soc. Jpn. 2009, 29, 236–241. [Google Scholar]
- Scarlat, R.C.; Heygster, G.; Pedersen, L.T. Experiences with an Optimal estimation algorithm for surface and atmospheric parameter retrieval from passive microwave data in the arctic. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3934–3947. [Google Scholar] [CrossRef]
- Bettenhausen, M.H.; Smith, C.K.; Bevilacqua, R.M.; Wang, N.Y.; Gaiser, P.W.; Cox, S. A nonlinear optimization algorithm for WindSat wind vector retrievals. IEEE Trans. Geosci. Remote Sens. 2006, 44, 597–610. [Google Scholar] [CrossRef]
- Ashcroft, P.; Wentz, F.J. AMSR-E/Aqua L2A Global Swath Spatially-Resampled Brightness Temperatures (Tb), Version 3. 2013. Available online: https://cmr.earthdata.nasa.gov/search/concepts/C190757121-NSIDC_ECS.html (accessed on 30 July 2016).
- Wentz, F.J. SSM/I Version-7 Calibration Report; Remote Sensing Systems: Santa Rosa, CA, USA; 2013; p. 46. [Google Scholar]
- Woodruff, S.D.; Worley, S.J.; Lubker, S.J.; Ji, Z.; Eric Freeman, J.; Berry, D.I.; Brohan, P.; Kent, E.C.; Reynolds, R.W.; Smith, S.R.; et al. ICOADS Release 2.5: Extensions and enhancements to the surface marine meteorological archive. Int. J. Climatol. 2011, 31, 951–967. [Google Scholar] [CrossRef]
- Good, S.A.; Martin, M.J.; Rayner, N.A. EN4: Quality controlled ocean temperature and salinity profiles and monthly objective analyses with uncertainty estimates: THE EN4 DATA SET. J. Geophys. Res. Oceans 2013, 118, 6704–6716. [Google Scholar] [CrossRef]
- O’Carroll, A.G.; Eyre, J.R.; Saunders, R.W. Three-Way Error Analysis between AATSR, AMSR-E, and In Situ sea surface temperature observations. J. Atmos. Ocean. Technol. 2008, 25, 1197–1207. [Google Scholar] [CrossRef]
- Atkinson, C.P.; Rayner, N.A.; Kennedy, J.J.; Good, S.A. An integrated database of ocean temperature and salinity observations. J. Geophys. Res. Oceans 2014, 119, 7139–7163. [Google Scholar] [CrossRef]
- Roemmich, D.; Johnson, G.; Riser, S.; Davis, R.; Gilson, J.; Owens, W.B.; Garzoli, S.; Schmid, C.; Ignaszewski, M. The Argo Program: Observing the Global Oceans with Profiling Floats. Oceanography 2009, 22, 34–43. [Google Scholar] [CrossRef]
- Gille, S.T. Decadal-Scale Temperature Trends in the Southern Hemisphere Ocean. J. Clim. 2008, 21, 4749–4765. [Google Scholar] [CrossRef]
- Kennedy, J.J. A review of uncertainty in in situ measurements and data sets of sea surface temperature: In situ sst uncertainty. Rev. Geophys. 2014, 52, 1–32. [Google Scholar] [CrossRef]
- Abraham, J.P.; Baringer, M.; Bindoff, N.L.; Boyer, T.; Cheng, L.J.; Church, J.A.; Conroy, J.L.; Domingues, C.M.; Fasullo, J.T.; Gilson, J.; et al. A review of global ocean temperature observations: Implications for ocean heat content estimates and climate change: Review of ocean observations. Rev. Geophys. 2013, 51, 450–483. [Google Scholar] [CrossRef]
- Embury, O.; Merchant, C.J.; Corlett, G.K. A reprocessing for climate of sea surface temperature from the along-track scanning radiometers: Initial validation, accounting for skin and diurnal variability effects. Remote Sens. Environ. 2012, 116, 62–78. [Google Scholar] [CrossRef]
- Høyer, J.L.; Karagali, I.; Dybkjær, G.; Tonboe, R. Multi sensor validation and error characteristics of Arctic satellite sea surface temperature observations. Remote Sens. Environ. 2012, 121, 335–346. [Google Scholar] [CrossRef]
- Merchant, C.J.; Embury, O.; Rayner, N.A.; Berry, D.I.; Corlett, G.K.; Lean, K.; Veal, K.L.; Kent, E.C.; Llewellyn-Jones, D.T.; Remedios, J.J.; et al. A 20 year independent record of sea surface temperature for climate from Along-Track Scanning Radiometers: SST for climate from atsrs. J. Geophys. Res. Oceans 2012, 117. [Google Scholar] [CrossRef]
- Udaya Bhaskar, T.V.S.; Rahman, S.H.; Pavan, I.D.; Ravichandran, M.; Nayak, S. Comparison of AMSR-E and TMI sea surface temperature with Argo near-surface temperature over the Indian Ocean. Int. J. Remote Sens. 2009, 30, 2669–2684. [Google Scholar] [CrossRef]
- Dee, D.P.; Uppala, S.M.; Simmons, A.J.; Berrisford, P.; Poli, P.; Kobayashi, S.; Andrae, U.; Balmaseda, M.A.; Balsamo, G.; Bauer, P.; et al. The ERA-Interim reanalysis: configuration and performance of the data assimilation system. Q. J. R. Meteorol. Soc. 2011, 137, 553–597. [Google Scholar] [CrossRef]
- Zweng, M.M.; Reagan, J.R.; Antonov, J.I.; Seidov, D.; Biddle, M.M. World Ocean Atlas 2013, Volume 2, Salinity. 2013. Available online: https://repository.library.noaa.gov/view/noaa/14848 (accessed on 26 June 2017).
- Boyer, T.P.; Antonov, J.I.; Baranova, O.K.; Garcia, H.E.; Johnson, D.R.; Mishonov, A.V.; O’Brien, T.D.; Seidov, D.; Smolyar, I.; Zweng, M.M.; et al. World Ocean Database 2013; NOAA Printing Office: Silver Spring, MD, USA, 2013; 208p. [Google Scholar]
- Block, T.; Embacher, S.; Merchant, C.J.; Donlon, C. High performance software framework for the calculation of satellite-to-satellite data matchups (MMS version 1.2). Geosci. Model Dev. Discuss. 2017, 1–15. [Google Scholar] [CrossRef]
- Schulzweida, U.; Kornblueh, L.; Quast, R. CDO User’s Guide—Climate Data Operators; Max Planck Institute for Meteorology: Hamburg, Germany, 2010; pp. 1–173. [Google Scholar]
- Gentemann, C.L.; Hilburn, K.A. In situ validation of sea surface temperatures from the GCOM-W1 AMSR2 RSS calibrated brightness temperatures: Validation of RSS GCOM-W1 SST. J. Geophys. Res. Oceans 2015, 120, 3567–3585. [Google Scholar] [CrossRef]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding—Theory and Practice; Series on Atmospheric Ocanic and Planetary Physics; World Scientific Publishing Co. Pte. Ltd.: Singapore, 2000; Volume 2, ISBN 978-981-281-371-8. [Google Scholar]
- Wentz, F.J.; Meissner, T. AMSR Ocean Algorithm. Algorithm Theoretical Basis Document; Remote Sensing Systems: Santa Rosa, CA, USA, 2000. [Google Scholar]
- Chelton, D.B.; Freilich, M.H. Scatterometer-based assessment of 10-m wind analyses from the operational ECMWF and NCEP Numerical weather prediction models. Mon. Weather Rev. 2005, 133, 409–429. [Google Scholar] [CrossRef]
- Jakobson, E.; Vihma, T.; Palo, T.; Jakobson, L.; Keernik, H.; Jaagus, J. Validation of atmospheric reanalyses over the central Arctic Ocean: Tara reanalyses validation. Geophys. Res. Lett. 2012, 39. [Google Scholar] [CrossRef]
- Li, J.-L.F.; Waliser, D.; Woods, C.; Teixeira, J.; Bacmeister, J.; Chern, J.; Shen, B.-W.; Tompkins, A.; Tao, W.-K.; Köhler, M. Comparisons of satellites liquid water estimates to ECMWF and GMAO analyses, 20th century IPCC AR4 climate simulations, and GCM simulations. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Jiang, J.H.; Su, H.; Zhai, C.; Perun, V.S.; Del Genio, A.; Nazarenko, L.S.; Donner, L.J.; Horowitz, L.; Seman, C.; Cole, J.; et al. Evaluation of cloud and water vapor simulations in CMIP5 climate models using NASA “A-Train” satellite observations: Evaluation of IPCC Ar5 model simulations. J. Geophys. Res. Amospheres 2012, 117. [Google Scholar] [CrossRef]
- Donlon, C.J.; Minnett, P.J.; Gentemann, C.; Nightingale, T.J.; Barton, I.J.; Ward, B.; Murray, M.J. Toward improved validation of satellite sea surface skin temperature measurements for climate research. J. Clim. 2002, 15, 353–369. [Google Scholar] [CrossRef]
- Meissner, T.; Wentz, F.J. The emissivity of the ocean surface between 6 and 90 GHz over a large range of wind speeds and earth incidence angles. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3004–3026. [Google Scholar] [CrossRef]
- Pascual, A.; Faugère, Y.; Larnicol, G.; Le Traon, P.-Y. Improved description of the ocean mesoscale variability by combining four satellite altimeters. Geophys. Res. Lett. 2006, 33. [Google Scholar] [CrossRef]
- Legeckis, R. A survey of worldwide sea surface temperature fronts detected by environmental satellites. J. Geophys. Res. 1978, 83. [Google Scholar] [CrossRef]
- Prigent, C.; Aires, F.; Bernardo, F.; Orlhac, J.-C.; Goutoule, J.-M.; Roquet, H.; Donlon, C. Analysis of the potential and limitations of microwave radiometry for the retrieval of sea surface temperature: Definition of MICROWAT, a new mission concept: Sea Temperature from Microwaves. J. Geophys. Res. Oceans 2013, 118, 3074–3086. [Google Scholar] [CrossRef]
- Gentemann, C.L.; Meissner, T.; Wentz, F.J. Accuracy of satellite sea surface temperatures at 7 and 11 GHz. IEEE Trans. Geosci. Remote Sens. 2010, 48, 1009–1018. [Google Scholar] [CrossRef]
- Merchant, C.J.; Harris, A.R.; Roquet, H.; Le Borgne, P. Retrieval characteristics of non-linear sea surface temperature from the advanced very high resolution radiometer. Geophys. Res. Lett. 2009, 36. [Google Scholar] [CrossRef]
- Castro, S.L.; Wick, G.A.; Jackson, D.L.; Emery, W.J. Error characterization of infrared and microwave satellite sea surface temperature products for merging and analysis. J. Geophys. Res. 2008, 113. [Google Scholar] [CrossRef]
- Dong, S.; Gille, S.T.; Sprintall, J.; Gentemann, C. Validation of the advanced microwave scanning radiometer for the earth observing system (AMSR-E) sea surface temperature in the southern ocean. J. Geophys. Res. 2006, 111. [Google Scholar] [CrossRef]













| Flagging | N | % Removed |
|---|---|---|
| All matchups | 7,278,035 | |
| Gross error flag | 6,323,288 | 13.1 |
| 13.1 | |
| 9.6 | |
| 6.5 | |
| 8.0 | |
| 0.4 | |
| All above checks | 4,286,354 | 41.1 |
| Even out by latitude | 3,764,798 | 12.2 |
| Total | 3,764,798 | 48.3 |
| Aspect of Optimal Estimator | Configuration |
|---|---|
| Initial forward model, iF(x) | Modified from Wentz et al. [54] (Section 2.3.1) |
| Channels used in retrieval | 6.9, 10.7, 18.7, 23.8, 36.5 GHz (V/H) |
| First guess fields, xa | NWP (Section 2.1.3) |
| Prior error covariance for SST, | 0.5 K |
| Error covariance of observations and model, Sϵ | Full matrix (Section 2.3.2) |
| Convergence criterion | . (Section 2.3.2) |
| IterationsImproved forward model, F(x) | Max iterations = 10iF(x) + corrections (Section 2.3.3) |
| Filter | Bias/K OE-Drifter | std/K OE-Drifter | Bias/K NWP-Drifter | std/K NWP-Drifter | N (106) | |
|---|---|---|---|---|---|---|
| Convergence test passed | 0.02 | 0.57 | −0.04 | 0.50 | 3.7429 | =100% |
| Gross error check | 0.04 | 0.54 | −0.04 | 0.50 | 3.4071 | =91% |
| RMSETB < 1 K | 0.02 | 0.51 | −0.04 | 0.50 | 3.4329 | =92% |
| RMSETB < 0.50 K | 0.02 | 0.47 | −0.04 | 0.48 | 2.3953 | =64% |
| RMSETB < 0.35 K | 0.02 | 0.45 | −0.04 | 0.47 | 1.5681 | =42% |
| Filter | Bias/K OE-Argo | std/K OE-Argo | Bias/K NWP-Argo | std/K NWP-Argo | N | |
|---|---|---|---|---|---|---|
| Convergence test passed | 0.01 | 0.61 | −0.05 | 0.55 | 57789 | =100% |
| Gross error check | 0.03 | 0.58 | −0.05 | 0.54 | 51846 | =90% |
| RMSETB < 1 K | 0.01 | 0.55 | −0.06 | 0.54 | 53150 | =92% |
| RMSETB < 0.50 K | 0.01 | 0.50 | −0.06 | 0.51 | 36639 | =63% |
| RMSETB < 0.35 K | 0.01 | 0.49 | −0.05 | 0.50 | 23410 | =41% |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Nielsen-Englyst, P.; L. Høyer, J.; Toudal Pedersen, L.; L. Gentemann, C.; Alerskans, E.; Block, T.; Donlon, C. Optimal Estimation of Sea Surface Temperature from AMSR-E. Remote Sens. 2018, 10, 229. https://doi.org/10.3390/rs10020229
Nielsen-Englyst P, L. Høyer J, Toudal Pedersen L, L. Gentemann C, Alerskans E, Block T, Donlon C. Optimal Estimation of Sea Surface Temperature from AMSR-E. Remote Sensing. 2018; 10(2):229. https://doi.org/10.3390/rs10020229
Chicago/Turabian StyleNielsen-Englyst, Pia, Jacob L. Høyer, Leif Toudal Pedersen, Chelle L. Gentemann, Emy Alerskans, Tom Block, and Craig Donlon. 2018. "Optimal Estimation of Sea Surface Temperature from AMSR-E" Remote Sensing 10, no. 2: 229. https://doi.org/10.3390/rs10020229
APA StyleNielsen-Englyst, P., L. Høyer, J., Toudal Pedersen, L., L. Gentemann, C., Alerskans, E., Block, T., & Donlon, C. (2018). Optimal Estimation of Sea Surface Temperature from AMSR-E. Remote Sensing, 10(2), 229. https://doi.org/10.3390/rs10020229