Estimation of High Spatial-Resolution Clear-Sky Land Surface-Upwelling Longwave Radiation from VIIRS/S-NPP Data
Abstract
:1. Introduction
2. Data
2.1. Visible Infrared Imaging Radiometer Suite (VIIRS) Data
2.2. Atmospheric Profiles
2.3. Surface Radiation Budget Network (SURFRAD)
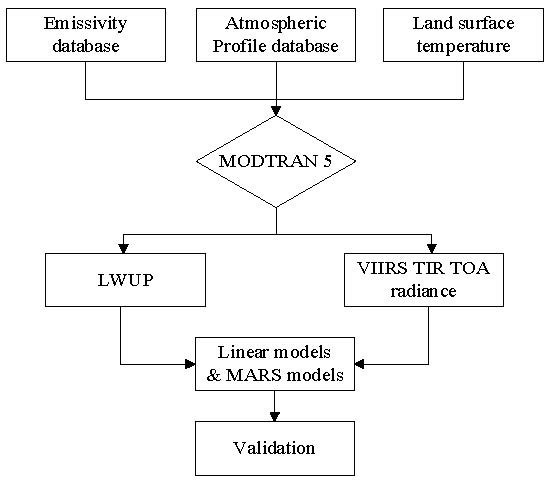
3. Method
3.1. Radiative Transfer Modeling
3.2. Linear Model
3.3. The Multivariate Adaptive Regression Spline (MARS) Model
4. Results
4.1. Training Results of the Linear Model and MARS Model
4.2. Validation with Field Measurements
4.2.1. The Linear Model
4.2.2. MARS Models
4.3. Comparison between Moderate Resolution Imaging Spectroradiometer (MODIS) and VIIRS Surface-Upwelling Longwave Radiation (LWUP)
5. Discussion
5.1. Cloud Effect
5.2. Broadband Emissivity (BBE) Effect
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Diak, G.R.; Mecikalski, J.R.; Anderson, M.C.; Norman, J.M.; Kustas, W.P.; Torn, R.D.; DeWolf, R.L. Estimating land surface energy budgets from space: Review and current efforts at the university of wisconsin—madison and usda–ars. Bull. Am. Meteorol. Soc. 2004, 85, 65–78. [Google Scholar] [CrossRef]
- Ellingson, R.G. Surface longwave fluxes from satellite observations: A critical review. Remote Sens. Environ. 1995, 51, 89–97. [Google Scholar] [CrossRef]
- Schmetz, J. Towards a surface radiation climatology: Retrieval of downward irradiances from satellites. Atmos. Res. 1989, 23, 287–321. [Google Scholar] [CrossRef]
- Curry, J.A.; Schramm, J.L.; Rossow, W.B.; Randall, D. Overview of arctic cloud and radiation characteristics. J. Clim. 1996, 9, 1731–1764. [Google Scholar] [CrossRef]
- Mlynczak, P.E.; Smith, G.L.; Wilber, A.C.; Stackhouse, P.W. Annual cycle of surface longwave radiation. J. Appl. Meteorol. Climatol. 2011, 50, 1212–1224. [Google Scholar] [CrossRef]
- Ma, Q.; Wang, K.; Wild, M. Evaluations of atmospheric downward longwave radiation from 44 coupled general circulation models of cmip5. J. Geophys. Res. Atmos. 2014, 119, 4486–4497. [Google Scholar] [CrossRef]
- Wang, W.; Liang, S.; Augustine, J.A. Estimating high spatial resolution clear-sky land surface upwelling longwave radiation from modis data. IEEE Trans. Geosci. Remote Sens. 2009, 47, 1559–1570. [Google Scholar] [CrossRef]
- Bisht, G.; Venturini, V.; Islam, S.; Jiang, L. Estimation of the net radiation using modis (moderate resolution imaging spectroradiometer) data for clear sky days. Remote Sens. Environ. 2005, 97, 52–67. [Google Scholar] [CrossRef]
- Long, D.; Gao, Y.; Singh, V.P. Estimation of daily average net radiation from modis data and dem over the baiyangdian watershed in north china for clear sky days. J. Hydrol. 2010, 388, 217–233. [Google Scholar] [CrossRef]
- Wang, C.; Tang, B.-H.; Huo, X.; Li, Z.-L. New method to estimate surface upwelling long-wave radiation from modis cloud-free data. Opt. Express 2017, 25, A574–A588. [Google Scholar] [CrossRef] [PubMed]
- Jiao, Z.; Yan, G.; Zhao, J.; Wang, T.; Chen, L. Estimation of surface upward longwave radiation from modis and viirs clear-sky data in the tibetan plateau. Remote Sens. Environ. 2015, 162, 221–237. [Google Scholar] [CrossRef]
- Cheng, J.; Liang, S. Global estimates for high-spatial-resolution clear-sky land surface upwelling longwave radiation from modis data. IEEE Trans. Geosci. Remote Sens. 2016, 54, 4115–4129. [Google Scholar] [CrossRef]
- Lee, H.-T.; Ellingson, R.G. Development of a nonlinear statistical method for estimating the downward longwave radiation at the surface from satellite observations. J. Atmos. Ocean. Technol. 2002, 19, 1500–1515. [Google Scholar] [CrossRef]
- Liang, S.; Zhao, X.; Liu, S.; Yuan, W.; Cheng, X.; Xiao, Z.; Zhang, X.; Liu, Q.; Cheng, J.; Tang, H. A long-term global land surface satellite (glass) data-set for environmental studies. Int. J. Digit. Earth 2013, 6, 5–33. [Google Scholar] [CrossRef]
- Cheng, J.; Liang, S.; Yao, Y.; Ren, B.; Shi, L.; Liu, H. A comparative study of three land surface broadband emissivity datasets from satellite data. Remote Sens. 2013, 6, 111–134. [Google Scholar] [CrossRef]
- Vogt, J.V. Land surface temperature retrieval from noaa avhrr data. In Advances in the Use of NOAA AVHRR Data for Land Applications; Springer: Berlin/Heidelberg, Germany, 1996; pp. 125–151. [Google Scholar]
- Wan, Z.; Dozier, J. A generalized split-window algorithm for retrieving land-surface temperature from space. IEEE Trans. Geosci. Remote Sens. 1996, 34, 892–905. [Google Scholar]
- Wan, Z.; Zhang, Y.; Zhang, Q.; Li, Z.-L. Quality assessment and validation of the modis global land surface temperature. Int. J. Remote Sens. 2004, 25, 261–274. [Google Scholar] [CrossRef]
- Cheng, J.; Liang, S.; Verhoef, W.; Shi, L.; Liu, Q. Estimating the hemispherical broadband longwave emissivity of global vegetated surfaces using a radiative transfer model. IEEE Trans. Geosci. Remote Sens. 2016, 54, 905–917. [Google Scholar] [CrossRef]
- Tang, B.; Li, Z.-L. Estimating of instananeous net surface longwave radiation from modis cloud-free data. Remote Sens. Environ. 2008, 112, 3482–3492. [Google Scholar] [CrossRef]
- Wang, T.; Yan, G.; Chen, L. Consistent retrieval methods to estimate land surface shortwave and longwave radiative flux components under clear-sky conditions. Remote Sens. Environ. 2012, 124, 61–71. [Google Scholar] [CrossRef]
- Jackson, J.M.; Liu, H.; Laszlo, I.; Kondragunta, S.; Remer, L.A.; Huang, J.; Huang, H.C. Suomi-npp viirs aerosol algorithms and data products. J. Geophys. Res. Atmos. 2013, 118, 12673–12689. [Google Scholar] [CrossRef]
- Vargas, M.; Miura, T.; Shabanov, N.; Kato, A. An initial assessment of suomi npp viirs vegetation index edr. J. Geophys. Res. Atmos. 2013, 118, 12301–312316. [Google Scholar] [CrossRef]
- Wang, D.; Liang, S.; He, T.; Yu, Y. Direct estimation of land surface albedo from viirs data: Algorithm improvement and preliminary validation. J. Geophys. Res. Atmos. 2013, 118, 12577–12586. [Google Scholar] [CrossRef]
- Yu, Y.; Privette, J.L.; Pinheiro, A.C. Analysis of the npoess viirs land surface temperature algorithm using modis data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2340–2350. [Google Scholar]
- Petrenko, B. Evaluation and selection of sst regression algorithms for jpss viirs. J. Geophys. Res. Atmos. 2014, 119, 4580–4599. [Google Scholar] [CrossRef]
- Schueler, C.F.; Clement, J.E.; Ardanuy, P.E.; Welsch, C.; DeLuccia, F.; Swenson, H. Npoess viirs sensor design overview. In Earth Observing Systems VI, Proceedings of the International Society for Optics and Photonics, San Diego, CA, USA, 29 July–4 August 2001; pp. 11–24. [Google Scholar]
- Xiong, X.; Butler, J.; Chiang, K.; Efremova, B.; Fulbright, J.; Lei, N.; McIntire, J.; Oudrari, H.; Sun, J.; Wang, Z. Viirs on-orbit calibration methodology and performance. J. Geophys. Res. Atmos. 2014, 119, 5065–5078. [Google Scholar] [CrossRef]
- Madhavan, S.; Brinkmann, J.; Wenny, B.N.; Wu, A.; Xiong, X. Evaluation of viirs and modis thermal emissive band calibration stability using ground target. Remote Sens. 2016, 8, 158. [Google Scholar] [CrossRef]
- Godin, R. Joint polar satellite system (jpss) viirs cloud mask (vcm) algorithm theoretical basis document (atbd). JPSS 2014, 474, 474-00033. [Google Scholar]
- Aumann, H.; Chanhine, M.T.; Gautier, C. Airs/amsu/hsb on the aqua mission: Design, science objectives, data products, and processing systems. IEEE Trans. Geosci. Remote Sens. 2003, 41, 253–264. [Google Scholar] [CrossRef]
- Aumann, H.; Elliott, D.; Strow, L. Validation of the radiometric stability of the atmospheric infrared sounder. In Earth Observing Systems XVII, Proceedings of the International Society for Optics and Photonics, San Diego, CA, USA, 14–16 August 2012; p. 85100T. [Google Scholar]
- Susskind, J.; Barnet, C.D.; Blaisdell, J.M. Retrieval of atmoshperic and surface parameters from airs/amsu/hsb data in the presence of clouds. IEEE Trans. Geosci. Remote Sens. 2003, 41, 390–409. [Google Scholar] [CrossRef]
- Augustine, J.A.; DeLuisi, J.J.; Long, C.N. Surfrad—A national surface radiation budget network for atmospheric research. Bull. Am. Meteorol. Soc. 2000, 81, 2341–2357. [Google Scholar] [CrossRef]
- Wang, K.; Dickinson, R.E. Global atmospheric downward longwave radiation at the surface from ground-based observations, satellite retrievals, and reanalyses. Rev. Geophys. 2013, 51, 150–185. [Google Scholar] [CrossRef]
- Augustine, J.A.; Dutton, E.G. Variability of the surface radiation budget over the united states from 1996 through 2011 from high-quality measurements. J. Geophys. Res. Atmos. 2013, 118, 43–53. [Google Scholar] [CrossRef]
- Berk, A.; Anderson, G.; Acharya, P.; Shettle, E. Modtran5. 2.0. 0 User’s Manual; Spectral Sciences Inc.: Burlington, MA, USA; Air Force Research Laboratory: Hanscom, MA, USA, 2008. [Google Scholar]
- Baldridge, A.; Hook, S.; Grove, C.; Rivera, G. The aster spectral library version 2.0. Remote Sens. Environ. 2009, 113, 711–715. [Google Scholar] [CrossRef]
- Snyder, W.C.; Wan, Z.; Zhang, Y.; Feng, Y.-Z. Classification-based emissivity for land surface temperature measurement from space. Int. J. Remote Sens. 1998, 19, 2753–2774. [Google Scholar] [CrossRef]
- Friedman, J.H. Multivariate adaptive regression splines. Ann. Stat. 1991, 1–67. [Google Scholar] [CrossRef]
- Gupta, S.K.; Kratz, D.P.; Wilber, A.C.; Nguyen, L.C. Validation of parameterized algorithms used to derive trmm–ceres surface radiative fluxes. J. Atmos. Ocean. Technol. 2004, 21, 742–752. [Google Scholar] [CrossRef]
- Wang, W.; Liang, S.; Meyers, T. Validating modis land surface temperature products using long-term nighttime ground measurements. Remote Sens. Environ. 2008, 112, 623–635. [Google Scholar] [CrossRef]
- Zhao, C.; Wang, Y.; Wang, Q.; Li, Z.; Wang, Z.; Liu, D. A new cloud and aerosol layer detection method based on micropulse lidar measurements. J. Geophys. Res. Atmos. 2014, 119, 6788–6802. [Google Scholar] [CrossRef]









| Name | Location | Elevation (m) | Land Cover | Time Period of Used Data |
|---|---|---|---|---|
| Bondville_IL | 40.0519°N, 88.3731°W | 230 | Cropland | 2014–2017 |
| Boulder_CO | 40.1249°N, 105.2368°W | 1689 | Grassland | 2014–2017 |
| Desert_Rock_NV | 36.6237°N, 116.0195°W | 1007 | Desert | 2014–2017 |
| Fort_Peck_MT | 48.3078°N, 105.1017°W | 634 | Grassland | 2014–2017 |
| Goodwin_Creek_MS | 34.2547°N, 89.873°W | 98 | Grassland | 2014–2017 |
| Penn_State_PA | 40.7201°N, 77.9309°W | 376 | Cropland | 2014–2017 |
| Sioux_Falls_SD | 43.7340°N, 96.6233°W | 473 | Grassland | 2014–2017 |
| Low-Latitude Region | ||||||||||
| Linear Model | MARS | |||||||||
| Angle | a0 | a1 | a2 | a3 | R2 | Bias | RMSE | R2 | Bias | RMSE |
| 0° | 124.404 | 2.687 | 119.530 | −93.350 | 0.989 | 0.00 | 8.82 | 0.990 | 0.00 | 8.53 |
| 15° | 126.927 | 2.833 | 121.603 | −95.997 | 0.988 | 0.00 | 8.97 | 0.993 | 0.00 | 8.54 |
| 30° | 135.126 | 3.434 | 128.092 | −104.459 | 0.988 | 0.00 | 9.13 | 0.989 | 0.00 | 8.71 |
| 45° | 151.431 | 5.290 | 139.829 | −120.664 | 0.985 | 0.00 | 10.46 | 0.986 | 0.00 | 9.03 |
| 60° | 182.429 | 12.293 | 157.379 | −149.538 | 0.977 | 0.00 | 13.02 | 0.982 | 0.00 | 10.13 |
| Middle-Latitude Region | ||||||||||
| Linear Model | MARS | |||||||||
| Angle | a0 | a1 | a2 | a3 | R2 | Bias | RMSE | R2 | Bias | RMSE |
| 0° | 99.959 | 1.747 | 104.644 | −73.428 | 0.993 | 0.00 | 6.94 | 0.993 | 0.00 | 6.64 |
| 15° | 101.853 | 1.769 | 106.772 | −75.933 | 0.992 | 0.00 | 7.04 | 0.993 | 0.00 | 6.84 |
| 30° | 108.090 | 1.922 | 113.550 | −84.018 | 0.992 | 0.00 | 7.39 | 0.992 | 0.00 | 7.18 |
| 45° | 120.822 | 2.647 | 126.401 | −99.870 | 0.990 | 0.00 | 8.11 | 0.991 | 0.00 | 7.88 |
| 60° | 146.517 | 6.157 | 148.690 | −129.866 | 0.985 | 0.00 | 9.79 | 0.987 | 0.00 | 8.24 |
| High-Latitude Region | ||||||||||
| Linear Model | MARS | |||||||||
| Angle | a0 | a1 | a2 | a3 | R2 | Bias | RMSE | R2 | Bias | RMSE |
| 0° | 77.525 | 0.915 | 87.049 | −50.963 | 0.995 | 0.00 | 5.27 | 0.996 | 0.00 | 4.8 |
| 15° | 79.219 | 1.588 | 88.103 | −52.734 | 0.995 | 0.00 | 5.16 | 0.996 | 0.00 | 4.85 |
| 30° | 82.928 | 1.339 | 94.582 | −59.759 | 0.995 | 0.00 | 5.41 | 0.996 | 0.00 | 5.11 |
| 45° | 90.741 | 1.020 | 107.407 | −73.892 | 0.994 | 0.00 | 5.91 | 0.994 | 0.00 | 5.80 |
| 60° | 107.699 | 1.298 | 132.253 | −102.344 | 0.991 | 0.00 | 6.95 | 0.992 | 0.00 | 6.47 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, S.; Cheng, J. Estimation of High Spatial-Resolution Clear-Sky Land Surface-Upwelling Longwave Radiation from VIIRS/S-NPP Data. Remote Sens. 2018, 10, 253. https://doi.org/10.3390/rs10020253
Zhou S, Cheng J. Estimation of High Spatial-Resolution Clear-Sky Land Surface-Upwelling Longwave Radiation from VIIRS/S-NPP Data. Remote Sensing. 2018; 10(2):253. https://doi.org/10.3390/rs10020253
Chicago/Turabian StyleZhou, Shugui, and Jie Cheng. 2018. "Estimation of High Spatial-Resolution Clear-Sky Land Surface-Upwelling Longwave Radiation from VIIRS/S-NPP Data" Remote Sensing 10, no. 2: 253. https://doi.org/10.3390/rs10020253
APA StyleZhou, S., & Cheng, J. (2018). Estimation of High Spatial-Resolution Clear-Sky Land Surface-Upwelling Longwave Radiation from VIIRS/S-NPP Data. Remote Sensing, 10(2), 253. https://doi.org/10.3390/rs10020253