Snow Wetness Retrieved from L-Band Radiometry
Abstract
:1. Introduction
2. Data Sets
2.1. Test Site
2.2. In-Situ Measurements
2.3. Radiometry Data
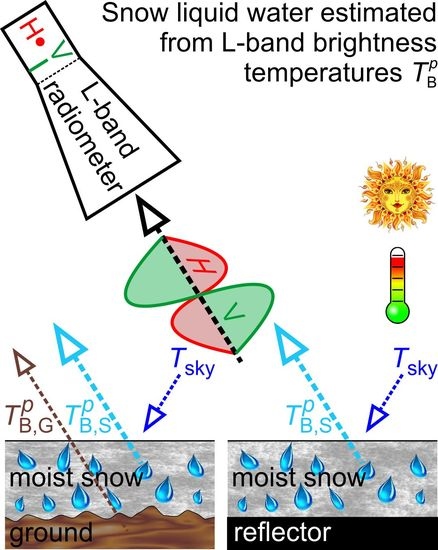
3. Retrieval Approach
3.1. Approach Used to Retrieve from
3.2. Approach Used to Retrieve from
4. Results and Discussion
4.1. Snow Wetness Retrieval Using
4.2. Snow Wetness Retrieval Using
- Brightness temperatures emitted exclusively from the “reflector area” are significantly more sensitive to low amounts of snow liquid water than brightness temperatures that are emitted from the “natural area”. This is demonstrated theoretically and experimentally in [22], and was the main reason for suggesting the use of retrievals as “references” to validate .
- are achieved from using a simple single parameter retrieval approach assuming ground reflectivity and using in-situ measured snow density (Figure 2b) as previous knowledge (Section 3.1). Accordingly, retrievals do not require the antecedent retrievals , as is the case in the two-step approach that is used to retrieve from (Section 3.2), implying that are not distorted by erroneous . The “pseudo-measurements” used in the first retrieval step are subject to errors introduced via snow liquid water content (Section 4.1 in [23]), spatially heterogeneous ground permittivity (Section 4.2 in [23]), and other types of geophysical noise [28].
5. Summary and Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Takala, M.; Luojus, K.; Pulliainen, J.; Derksen, C.; Lemmetyinen, J.; Kärnä, J.P.; Bojkov, B. Estimating northern hemisphere snow water equivalent for climate research through assimilation of space-borne radiometer data and ground-based measurements. Remote Sens. Environ. 2011, 115, 3517–3529. [Google Scholar] [CrossRef]
- Derksen, C.; Brown, R. Spring snow cover extent reductions in the 2008–2012 period exceeding climate model projections. Geophys. Res. Lett. 2012, 39, 19. [Google Scholar] [CrossRef]
- Mudryk, L.; Derksen, C.; Kushner, P.; Brown, R. Characterization of Northern Hemisphere snow water equivalent datasets, 1981–2010. J. Clim. 2015, 28, 8037–8051. [Google Scholar] [CrossRef]
- Barnett, T.P.; Adam, J.C.; Lettenmaier, D.P. Potential impacts of a warming climate on water availability in snow-dominated regions. Nature 2005, 438, 303–309. [Google Scholar] [CrossRef] [PubMed]
- Diffenbaugh, N.S.; Scherer, M.; Ashfaq, M. Response of snow-dependent hydrologic extremes to continued global warming. Nat. Clim. Chang. 2013, 3, 379. [Google Scholar] [CrossRef] [PubMed]
- Mankin, J.S.; Viviroli, D.; Singh, D.; Hoekstra, A.Y.; Diffenbaugh, N.S. The potential for snow to supply human water demand in the present and future. Environ. Res. Lett. 2015, 10, 114016. [Google Scholar] [CrossRef]
- Brun, E. Investigation on Wet-Snow Metamorphism in Respect of Liquid-Water Content. Ann. Glaciol. 1989, 13, 22–26. [Google Scholar] [CrossRef]
- Jiancheng, S.; Dozier, J.; Rott, H. Deriving snow liquid water content using C-band polarimetric SAR. In Proceedings of the 1993 Better Understanding of Earth Environment, International Geoscience and Remote Sensing Symposium, IGARSS ‘93, Tokyo, Japan, 18–21 August 1993; Volume 3, pp. 1038–1041. [Google Scholar]
- Mätzler, C. Thermal Microwave Radiation: Applications for Remote Sensing; IEE Electromagnetic Waves Series No. 52; The Institution of Engineering and Technology: London, UK, 2006. [Google Scholar]
- Stiles, W.H.; Ulaby, F.T. The active and passive microwave response to snow parameters: 1. Wetness. J. Geophys. Res. Oceans 1980, 85, 1037–1044. [Google Scholar] [CrossRef]
- Mätzler, C.; Schanda, E. Snow mapping with active microwave sensors. Int. J. Remote Sens. 1984, 5, 409–422. [Google Scholar] [CrossRef]
- Arslan, A.N.; Hallikainen, M.T.; Pulliainen, J.T. Investigating of snow wetness parameter using a two-phase backscattering model. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1827–1833. [Google Scholar] [CrossRef]
- Kennedy, J.; Sakamoto, R. Passive microwave determinations of snow wetness factors. In Proceedings of the 4th International Symposium on Remote Sensing of Environment, Ann Arbor, MI, USA, 12–14 April 1966; pp. 161–171. [Google Scholar]
- Hofer, R.; Mätzler, C. Investigations on snow parameters by radiometry in the 3- to 60-mm wavelength region. J. Geophys. Res. 1980, 85, 453. [Google Scholar] [CrossRef]
- Schanda, E.; Matzler, C.; Kunzi, K. Microwave remote sensing of snow cover. Int. J. Remote Sens. 1983, 4, 149–158. [Google Scholar] [CrossRef]
- Matzler, C.; Strozzi, T.; Weise, T.; Floricioiu, D.-M.; Rott, H. Microwave snowpack studies made in the Austrian Alps during the SIR-C/X-SAR experiment. Int. J. Remote Sens. 1997, 18, 2505–2530. [Google Scholar] [CrossRef]
- Shi, J.; Dozier, J. Inferring snow wetness using C-band data from SIR-C’s polarimetric synthetic aperture radar. IEEE Trans. Geosci. Remote Sens. 1995, 33, 905–914. [Google Scholar]
- Sun, C.; Neale, C.M.; McDonnell, J.J. Snow wetness estimates of vegetated terrain from satellite passive microwave data. Hydrol. Process. 1996, 10, 1619–1628. [Google Scholar] [CrossRef]
- Stein, J.; Kane, D.L. Monitoring the unfrozen water content of soil and snow using time domain reflectometry. Water Resour. Res. 1983, 19, 1573–1584. [Google Scholar] [CrossRef]
- Schneebeli, M.; Davis, R. Time-Domain Reflectometry as a Method to Measure Snow Wetness and Density. In Proceedings of the International Snow Science Workshop, Beckenridge, Colorado Avalanche Information Centre, Denver, CO, USA, 4–8 October 1992; pp. 36–364. [Google Scholar]
- Schneebeli, M.; Coléou, C.; Touvier, F.; Lesaffre, B. Measurement of density and wetness in snow using time-domain reflectometry. Ann. Glaciol. 1998, 26, 69–72. [Google Scholar] [CrossRef]
- Naderpour, R.; Schwank, M.; Mätzler, C. Davos-Laret Remote Sensing Field Laboratory: 2016/2017 Winter Season L-Band Measurements Data-Processing and Analysis. Remote Sens. 2017, 9, 1185. [Google Scholar] [CrossRef]
- Schwank, M.; Naderpour, R. Snow Density and Ground Permittivity Retrieved from L-Band Radiometry: Melting Effects. Remote Sens. 2018, 10, 354. [Google Scholar]
- Schwank, M.; Mätzler, C.; Wiesmann, A.; Wegmüller, U.; Pulliainen, J.; Lemmetyinen, J.; Drusch, M. Snow Density and Ground Permittivity Retrieved from L-Band Radiometry: A Synthetic Analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3833–3845. [Google Scholar] [CrossRef]
- Lemmetyinen, J.; Schwank, M.; Rautiainen, K.; Kontu, A.; Parkkinen, T.; Mätzler, C.; Roy, A. Snow density and ground permittivity retrieved from L-band radiometry: Application to experimental data. Remote Sens. Environ. 2016, 180, 377–391. [Google Scholar] [CrossRef]
- Roy, A.; Toose, P.; Williamson, M.; Rowlandson, T.; Derksen, C.; Royer, A.; Arnold, L. Response of L-Band brightness temperatures to freeze/thaw and snow dynamics in a prairie environment from ground-based radiometer measurements. Remote Sens. Environ. 2017, 191, 67–80. [Google Scholar] [CrossRef]
- Schwank, M.; Rautiainen, K.; Mätzler, C.; Stähli, M.; Lemmetyinen, J.; Pulliainen, J.; Drusch, M. Model for microwave emission of a snow-covered ground with focus on L band. Remote Sens. Environ. 2014, 154, 180–191. [Google Scholar] [CrossRef]
- Naderpour, R.; Schwank, M.; Mätzler, C.; Lemmetyinen, J.; Steffen, K. Snow Density and Ground Permittivity Retrieved From L-Band Radiometry: A Retrieval Sensitivity Analysis. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3148–3161. [Google Scholar] [CrossRef]
- Schwank, M.; Wiesmann, A.; Werner, C.; Mätzler, C.; Weber, D.; Murk, A.; Wegmüller, U. ELBARA II, An L-Band Radiometer System for Soil Moisture Research. Sensors 2010, 10, 584–612. [Google Scholar] [CrossRef] [PubMed]
- Wiesmann, A.; Mätzler, C. Microwave emission model of layered snowpacks. Remote Sens. Environ. 1999, 70, 307–316. [Google Scholar] [CrossRef]
- Schwank, M.; Wigneron, J.P.; Lopez-Baeza, E.; Völksch, I.; Mätzler, C.; Kerr, Y. L-Band Radiative Properties of Vine Vegetation at the SMOS Cal/Val Site MELBEX III. IEEE Trans. Geosci. Remote Sens. 2012, 50, 1587–1601. [Google Scholar] [CrossRef] [Green Version]
- Mätzler, C.; Aebischer, H.; Schanda, E. Microwave dielectric properties of surface snow. IEEE J. Ocean. Eng. 1984, 9, 366–371. [Google Scholar] [CrossRef]
- Pomeroy, J.; Brun, E. Physical properties of snow. In Snow Ecology: An Interdisciplinary Examination of Snow-Covered Ecosystems; Springer: Dordrecht, The Netherlands, 2001; pp. 45–126. [Google Scholar]
- Bergstroem, S. The development of a snow routine for the HBV-2 model. Hydrol. Res. 1975, 6, 73–92. [Google Scholar]
- Kuusisto, E. On the values and variability of degree-day melting factor in Finland. Hydrol. Res. 1980, 11, 235–242. [Google Scholar]
- Martinec, J.; Rango, A.; Major, E. The Snowmelt-Runoff Model (SRM) User’s Manual; NASA: Washington, DC, USA, 1983.
- Lang, H.; Braun, L. On the information content of air temperature in the context of snow melt estimation. IAHS Publ. 1990, 190, 347–354. [Google Scholar]
- Wilson, W.T. An outline of the thermodynamics of snow-melt. Eos Trans. Am. Geophys. Union 1941, 22, 182–195. [Google Scholar] [CrossRef]
- Mätzler, C. Microwave permittivity of dry snow. IEEE Trans. Geosci. Remote Sens. 1996, 34, 573–581. [Google Scholar] [CrossRef]








© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Naderpour, R.; Schwank, M. Snow Wetness Retrieved from L-Band Radiometry. Remote Sens. 2018, 10, 359. https://doi.org/10.3390/rs10030359
Naderpour R, Schwank M. Snow Wetness Retrieved from L-Band Radiometry. Remote Sensing. 2018; 10(3):359. https://doi.org/10.3390/rs10030359
Chicago/Turabian StyleNaderpour, Reza, and Mike Schwank. 2018. "Snow Wetness Retrieved from L-Band Radiometry" Remote Sensing 10, no. 3: 359. https://doi.org/10.3390/rs10030359
APA StyleNaderpour, R., & Schwank, M. (2018). Snow Wetness Retrieved from L-Band Radiometry. Remote Sensing, 10(3), 359. https://doi.org/10.3390/rs10030359