Sparse Bayesian Learning Based Three-Dimensional Imaging Algorithm for Off-Grid Air Targets in MIMO Radar Array
Abstract
:1. Introduction
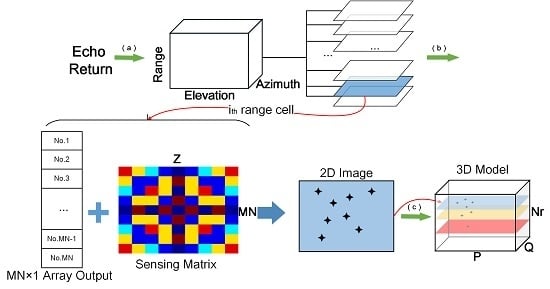
2. Problem Formulation of 3D Imaging
2.1. Ideal Imaging Model Based on Sparse Antenna Array
2.2. Off-Grid Imaging Model Using Taylor Expansion
3. The Proposed Off-Grid Imaging Algorithm
3.1. Algorithm Description
3.1.1. The Three-Stage Sparse Prior Model
3.1.2. Variational Inference EM Based Sparse Recovery Algorithm
3.2. Bayesian Cramér-Rao Bounds For Off-Grid Biases
4. Experimental Results
4.1. Validation of The Proposed Algorithm
4.2. Super-Resolution Performance Versus SNR
4.3. BCRB for Off-Grid Biases
5. Conclusions
Author Contributions
Conflicts of Interest
References
- Wang, G.; Xia, X.G.; Chen, V.C. Three-dimensional ISAR imaging of maneuvering targets using three receivers. IEEE Trans. Image Process. 2001, 10, 436–447. [Google Scholar] [CrossRef] [PubMed]
- Duan, G.Q.; Wang, D.W.; Ma, X.Y.; Su, Y. Three-dimensional imaging via wideband MIMO radar system. IEEE Geosci. Remote Sens. Lett. 2010, 7, 445–449. [Google Scholar] [CrossRef]
- Ma, C.; Yeo, T.S.; Tan, C.S.; Li, J.Y.; Shang, Y. Three-dimensional imaging using colocated MIMO radar and ISAR technique. IEEE Trans. Geosci. Remote Sens. 2012, 50, 3189–3201. [Google Scholar] [CrossRef]
- Ding, S.; Tong, N.; Zhang, Y.; Hu, X. Super-resolution 3D imaging in MIMO radar using spectrum estimation theory. IET Radar Sonar Navig. 2016, 11, 304–312. [Google Scholar] [CrossRef]
- Ma, C.; Yeo, T.S.; Tan, H.S.; Wang, J.; Chen, B. Three-dimensional ISAR imaging using a two-dimensional sparse antenna array. IEEE Geosci. Remote Sens. Lett. 2008, 5, 378–382. [Google Scholar]
- Ma, C.; Yeo, T.S.; Tan, C.S.; Liu, Z. Three-dimensional imaging of targets using colocated MIMO radar. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3009–3021. [Google Scholar] [CrossRef]
- Gu, F.; Chi, L.; Zhang, Q.; Zhu, F. Single snapshot imaging method in multiple-input multiple-output radar with sparse antenna array. IET Radar Sonar Navig. 2013, 7, 535–543. [Google Scholar] [CrossRef]
- Donoho, D.L. Compressed sensing. IEEE Trans. Inf. Theory 2006, 52, 1289–1306. [Google Scholar] [CrossRef]
- Zhang, L.; Xing, M.; Qiu, C.W.; Li, J.; Sheng, J.; Li, Y.; Bao, Z. Resolution enhancement for inversed synthetic aperture radar imaging under low SNR via improved compressive sensing. IEEE Trans. Geosci. Remote Sens. 2010, 48, 3824–3838. [Google Scholar] [CrossRef]
- Liu, H.; Jiu, B.; Liu, H.; Bao, Z. Superresolution ISAR imaging based on sparse Bayesian learning. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5005–5013. [Google Scholar]
- Xu, G.; Xing, M.; Zhang, L.; Liu, Y.; Li, Y. Bayesian inverse synthetic aperture radar imaging. IEEE Geosci. Remote Sens. Lett. 2011, 8, 1150–1154. [Google Scholar] [CrossRef]
- Hu, X.; Tong, N.; Zhang, Y.; Hu, G.; He, X. Multiple-input–multiple-output radar super-resolution three-dimensional imaging based on a dimension-reduction compressive sensing. IET Radar Sonar Navig. 2016, 10, 757–764. [Google Scholar] [CrossRef]
- Fannjiang, A.; Tseng, H.C. Compressive radar with off-grid targets: A perturbation approach. Inverse Probl. 2013, 29. [Google Scholar] [CrossRef]
- Yang, Z.; Xie, L. On gridless sparse methods for line spectral estimation from complete and incomplete data. IEEE Trans. Signal Process. 2015, 63, 3139–3153. [Google Scholar] [CrossRef]
- Boche, H.; Calderbank, R.; Kutyniok, G.; Vybiral, J. Compressed Sensing and Its Applications; Springer: Berlin, Germany, 2015; pp. 75–93. [Google Scholar]
- He, X.; Liu, C.; Liu, B.; Wang, D. Sparse frequency diverse MIMO radar imaging for off-grid target based on adaptive iterative MAP. Remote Sens. 2013, 5, 631–647. [Google Scholar] [CrossRef] [Green Version]
- Chi, Y.; Scharf, L.L.; Pezeshki, A.; Calderbank, A.R. Sensitivity to basis mismatch in compressed sensing. IEEE Trans. Signal Process. 2011, 59, 2182–2195. [Google Scholar] [CrossRef]
- Zhu, H.; Leus, G.; Giannakis, G.B. Sparsity-cognizant total least-squares for perturbed compressive sampling. IEEE Trans. Signal Process. 2011, 59, 2002–2016. [Google Scholar] [CrossRef]
- Yang, Z.; Xie, L.; Zhang, C. Off-grid direction of arrival estimation using sparse Bayesian inference. IEEE Trans. Signal Process. 2013, 61, 38–43. [Google Scholar] [CrossRef]
- Das, A. Theoretical and Experimental Comparison of Off-Grid Sparse Bayesian Direction-of-Arrival Estimation Algorithms. IEEE Access. 2017, 5, 18075–18087. [Google Scholar] [CrossRef]
- Bishop, C.M. Pattern Recognition and Machine Learning; Springer: Berlin, Germany, 2006. [Google Scholar]
- Blei, D.M.; Kucukelbir, A.; McAuliffe, J.D. Variational inference: A review for statisticians. J. Am. Stat. Assoc. 2017, 112. [Google Scholar] [CrossRef]
- Tzikas, D.G.; Likas, A.C.; Galatsanos, N.P. The variational approximation for Bayesian inference. IEEE Signal Process. Mag. 2008, 25, 131–146. [Google Scholar] [CrossRef]
- Lemonte, A.J.; Cordeiro, G.M. The exponentiated generalized inverse Gaussian distribution. Stat. Probab. Lett. 2011, 81, 506–517. [Google Scholar] [CrossRef]
- Prasad, R.; Murthy, C.R. Cramér-Rao-type bounds for sparse Bayesian learning. IEEE Trans. Signal Process. 2013, 61, 622–632. [Google Scholar] [CrossRef]











| Processing Steps of the Off-Grid Imaging Method. |
|---|
| Input: |
| Initialization: |
| , , , , |
| Iteration: let i denotes the iteration counter |
| (1) update by Equation (30) |
| (2) update by Equation (32) |
| (3) update by Equation (34) |
| (4) update by Equation (36) |
| (5) update and by Equations (37) and (39) |
| Termination condition: |
| The iteration ends when . |
| Output: |
| The imaging result , the off-gird bias estimation and |
| Parameter | Symbol | Value |
|---|---|---|
| Bandwidth | B | 500 MHz |
| Carrier frequency | 10 GHz | |
| Baseline in the X-direction | 6 m | |
| Baseline in the Y-direction | 6 m | |
| Target range | R | 2500 m |
| Pulse width | 10 s | |
| Number of transmitters | M | 4 |
| Number of receivers | N | 225 |
| Algorithm | OMP | BP | S-TLS | OGSBI | Proposed Method |
|---|---|---|---|---|---|
| NMSE of | 1.3371 | 1.1129 | 0.6921 | 0.5397 | 0.3016 |
| NMSE of | * | * | 0.6048 | 0.2452 | 0.1333 |
| NMSE of | * | * | 0.6321 | 0.2283 | 0.1266 |
| OGSBI, SNR = 10 dB | 0.0064 | 0.9932 | 0.5682 | 0.0490 |
| OGSBI, SNR = 20 dB | −0.0064 | 0.9949 | 0.2857 | 0.0412 |
| Proposed method, SNR = 10 dB | 0.0014 | 0.9948 | 0.4726 | 0.0418 |
| Proposed method, SNR = 20 dB | −0.0080 | 0.9975 | 0.2553 | 0.0435 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiao, Z.; Ding, C.; Liang, X.; Chen, L.; Zhang, F. Sparse Bayesian Learning Based Three-Dimensional Imaging Algorithm for Off-Grid Air Targets in MIMO Radar Array. Remote Sens. 2018, 10, 369. https://doi.org/10.3390/rs10030369
Jiao Z, Ding C, Liang X, Chen L, Zhang F. Sparse Bayesian Learning Based Three-Dimensional Imaging Algorithm for Off-Grid Air Targets in MIMO Radar Array. Remote Sensing. 2018; 10(3):369. https://doi.org/10.3390/rs10030369
Chicago/Turabian StyleJiao, Zekun, Chibiao Ding, Xingdong Liang, Longyong Chen, and Fubo Zhang. 2018. "Sparse Bayesian Learning Based Three-Dimensional Imaging Algorithm for Off-Grid Air Targets in MIMO Radar Array" Remote Sensing 10, no. 3: 369. https://doi.org/10.3390/rs10030369
APA StyleJiao, Z., Ding, C., Liang, X., Chen, L., & Zhang, F. (2018). Sparse Bayesian Learning Based Three-Dimensional Imaging Algorithm for Off-Grid Air Targets in MIMO Radar Array. Remote Sensing, 10(3), 369. https://doi.org/10.3390/rs10030369