Characterizing Land Surface Anisotropic Reflectance over Rugged Terrain: A Review of Concepts and Recent Developments
Abstract
:1. Introduction
2. BRDF in Rugged Terrain
2.1. Literatures Review
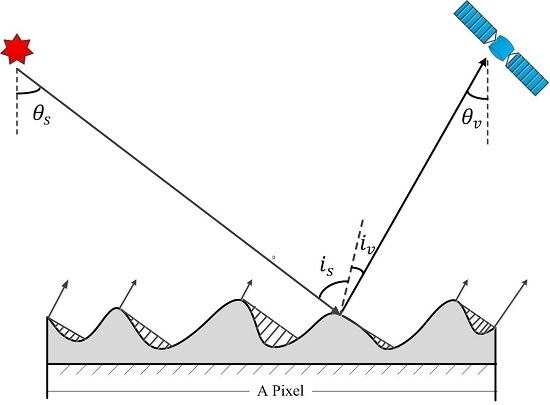
2.2. BRDF Definition and Its Topographic Effects
2.3. Model Building Procedures and Scientific Problems
3. Remote Sensing Atmospheric Correction over Rugged Terrain
3.1. Lambertian-Based Atmospheric Correction
3.2. Non-Lambertian-Based Atmospheric Correction
4. Solo Slope BRDF Model
4.1. Physical Basis
4.2. Model Development
4.2.1. Radiative Transfer Model
4.2.2. Geometric-Optical Model
4.2.3. Hybrid Model
4.3. Topographic Effect on Solo Slope BRDF
5. Composite Slope BRDF Model
5.1. Physical Basis
5.2. Model Development
5.2.1. Special-Shape Based Model
5.2.2. Random Field Based Model
5.2.3. DEM-Based Model
5.3. Topographic Effect on Composite Slope BRDF
6. Future Development and Perspective on BRDF Products Generation
6.1. High Quality DEM
6.2. Topographic Factor Parameterization
6.3. Potential Method to Derive the BRDF Product over Rugged Terrain
6.4. Validation Methods for the BRDF over Rugged Terrain
7. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Li, A.; Jiang, J.; Bian, J.; Deng, W. Combining the matter element model with the associated function of probability transformation for multi-source remote sensing data classification in mountainous regions. ISPRS J. Photogramm. Remote Sens. 2012, 67, 80–92. [Google Scholar] [CrossRef]
- Vanonckelen, S.; Lhermitte, S.; Rompaey, A.V. The effect of atmospheric and topographic correction methods on land cover classification accuracy. Int. J. Appl. Earth Obs. Geoinf. 2013, 24, 9–21. [Google Scholar] [CrossRef]
- Helbig, N.; Löwe, H. Shortwave radiation parameterization scheme for subgrid topography. J. Geophys. Res. Atmos. 2012, 117, 812–819. [Google Scholar] [CrossRef]
- Wen, J.; Zhao, X.; Liu, Q.; Tang, Y.; Dou, B. An improved land-surface albedo algorithm with DEM in rugged terrain. IEEE Geosci. Remote Sens. Lett. 2013, 11, 883–887. [Google Scholar]
- Yan, G.; Wang, T.; Jiao, Z.; Mu, X.; Zhao, J.; Chen, L. Topographic radiation modeling and spatial scaling of clear-sky land surface longwave radiation over rugged terrain. Remote Sens. Environ. 2016, 172, 15–27. [Google Scholar] [CrossRef]
- Pasolli, L.; Asam, S.; Castelli, M.; Bruzzone, L.; Wohlfahrt, G.; Zebisch, M.; Notarnicola, C. Retrieval of leaf area index in mountain grasslands in the alps from MODIS satellite imagery. Remote Sens. Environ. 2015, 165, 159–174. [Google Scholar] [CrossRef]
- Zhao, P.; Fan, W.; Liu, Y.; Mu, X.; Xu, X.; Peng, J. Study of the remote sensing model of FAPAR over rugged terrains. Remote Sens. 2016, 8, 309. [Google Scholar] [CrossRef]
- Schaepman-Strub, G.; Schaepman, M.E.; Painter, T.H.; Dangel, S.; Martonchik, J.V. Reflectance quantities in optical remote sensing—Definitions and case studies. Remote Sens. Environ. 2006, 103, 27–42. [Google Scholar] [CrossRef]
- Gao, F.; Schaaf, C.B.; Strahler, A.H.; Jin, Y.; Li, X. Detecting vegetation structure using a kernel-based BRDF model. Remote Sens. Environ. 2003, 86, 198–205. [Google Scholar] [CrossRef]
- Schaaf, C.B.; Gao, F.; Strahler, A.H.; Lucht, W.; Li, X.; Tsang, T.; Strugnell, N.C.; Zhang, X.; Jin, Y.; Muller, J.-P. First operational BRDF, albedo nadir reflectance products from MODIS. Remote Sens. Environ. 2002, 83, 135–148. [Google Scholar] [CrossRef]
- Xiao, Z.; Liang, S.; Wang, J.; Jiang, B.; Li, X. Real-time retrieval of leaf area index from MODIS time series data. Remote Sens. Environ. 2011, 115, 97–106. [Google Scholar] [CrossRef]
- Zege, E.P.; Katsev, I.L.; Malinka, A.V.; Prikhach, A.S.; Heygster, G.; Wiebe, H. Algorithm for retrieval of the effective snow grain size and pollution amount from satellite measurements. Remote Sens. Environ. 2011, 115, 2674–2685. [Google Scholar] [CrossRef]
- Roy, D.P.; Li, J.; Zhang, H.K.; Yan, L.; Huang, H.; Li, Z. Examination of Sentinel-2a multi-spectral instrument (MSI) reflectance anisotropy and the suitability of a general method to normalize MSI reflectance to nadir BRDFadjusted reflectance. Remote Sens. Environ. 2017, 199, 25–38. [Google Scholar] [CrossRef]
- Roy, D.P.; Zhang, H.K.; Ju, J.; Gomez-Dans, J.L.; Lewis, P.E.; Schaaf, C.B.; Sun, Q.; Li, J.; Huang, H.; Kovalskyy, V. A general method to normalize Landsat reflectance data to nadir BRDF adjusted reflectance. Remote Sens. Environ. 2016, 176, 255–271. [Google Scholar] [CrossRef]
- Schläpfer, D.; Richter, R.; Feingersh, T. Operational BRDF effects correction for wide-field-of-view optical scanners (BREFCOR). IEEE Trans. Geosci. Remote Sens. 2014, 53, 1855–1864. [Google Scholar] [CrossRef]
- Bacour, C.; Bréon, F.-M.; Maignan, F. Normalization of the directional effects in NOAA–AVHRR reflectance measurements for an improved monitoring of vegetation cycles. Remote Sens. Environ. 2006, 102, 402–413. [Google Scholar] [CrossRef]
- Fan, W.; Chen, J.M.; Ju, W.; Zhu, G. GOST: A geometric-optical model for sloping terrains. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5469–5482. [Google Scholar]
- Li, F.; Jupp, D.L.B.; Thankappan, M.; Lymburner, L.; Mueller, N.; Lewis, A.; Held, A. A physics-based atmospheric and BRDF correction for Landsat data over mountainous terrain. Remote Sens. Environ. 2012, 124, 756–770. [Google Scholar] [CrossRef]
- Wen, J.; Liu, Q.; Tang, Y.; Dou, B.; You, D.; Xiao, Q.; Liu, Q.; Li, X. Modeling land surface reflectance coupled BRDF for HJ-1/CCD data of rugged terrain in Heihe river basin, China. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 1506–1518. [Google Scholar] [CrossRef]
- Yin, G.; Li, A.; Zhao, W.; Jin, H.; Bian, J.; Wu, S. Modeling canopy reflectance over sloping terrain based on path length correction. IEEE Trans. Geosci. Remote Sens. 2017, 55, 4597–4609. [Google Scholar] [CrossRef]
- Schaaf, C.; Li, X.; Strahler, A. Topographic effects on bidirectional and hemispherical reflectances calculated with a geometric-optical canopy model. IEEE Trans. Geosci. Remote Sens. 1994, 32, 1186–1193. [Google Scholar] [CrossRef]
- Croft, H.; Anderson, K.; Kuhn, N.J. Reflectance anisotropy for measuring soil surface roughness of multiple soil types. Catena 2012, 93, 87–96. [Google Scholar] [CrossRef]
- Wang, Z.; Coburn, C.A.; Ren, X.; Teillet, P.M. Effect of surface roughness, wavelength, illumination, and viewing zenith angles on soil surface BRDF using an imaging BRDF approach. Int. J. Remote Sens. 2014, 35, 6894–6913. [Google Scholar] [CrossRef]
- Fan, W.; Chen, J.M.; Ju, W.; Nesbitt, N. Hybrid geometric optical–radiative transfer model suitable for forests on slopes. IEEE Trans. Geosci. Remote Sens. 2014, 52, 5579–5586. [Google Scholar]
- Proy, C.; Tanre, D.; Deschamps, P.Y. Evaluation of topographic effects in remotely sensed data. Remote Sens. Environ. 1989, 30, 21–32. [Google Scholar] [CrossRef]
- Shepherd, J.D.; Dymond, J.R. Correcting satellite imagery for the variance of reflectance and illumination with topography. Int. J. Remote Sens. 2003, 24, 3503–3514. [Google Scholar] [CrossRef]
- Combal, B.; Isaka, H.; Trotter, C. Extending a turbid medium BRDF model to allow sloping terrain with a vertical plant stand. IEEE Trans. Geosci. Remote Sens. 2000, 38, 798–810. [Google Scholar] [CrossRef]
- Wang, K.; Zhou, X.; Liu, J.; Sparrow, M. Estimating surface solar radiation over complex terrain using moderate-resolution satellite sensor data. Int. J. Remote Sens. 2005, 26, 47–58. [Google Scholar] [CrossRef]
- Wen, J.G.; Qiang, L.; Liu, Q.H.; Xiao, Q.; Li, X.W. Scale effect and scale correction of land-surface albedo in rugged terrain. Int. J. Remote Sens. 2009, 30, 5397–5420. [Google Scholar] [CrossRef]
- Hapke, B. Bidirectional reflectance spectroscopy: 3. Correction for macroscopic roughness. Icarus 1984, 59, 41–59. [Google Scholar] [CrossRef]
- Roupioz, L.; Nerry, F.; Jia, L.; Menenti, M. Improved surface reflectance from remote sensing data with sub-pixel topographic information. Remote Sens. 2014, 6, 10356–10374. [Google Scholar] [CrossRef]
- NicoDEMus, F.E.; Richmond, J.C.; Hsia, J.J.; Ginsberg, I.W.; Limperis, T. Geometrical Considerations and Nomenclature for Reflectance; Radiometry; Jones and Bartlett Publishers, Inc.: Burlington, MA, USA, 1977; pp. 94–145. [Google Scholar]
- Girolamo, L.D. Generalizing the definition of the bi-directional reflectance distribution function. Remote Sens. Environ. 2003, 88, 479–482. [Google Scholar] [CrossRef]
- Snyder, W.C. Definition and invariance properties of structured surface BRDF. IEEE Trans. Geosci. Remote Sens. 2002, 40, 1032–1037. [Google Scholar] [CrossRef]
- Parviainen, H.; Muinonen, K. Rough-surface shadowing of self-affine random rough surfaces. J. Quant. Spectrosc. Radiat. Transf. 2007, 106, 398–416. [Google Scholar] [CrossRef]
- Combal, B.; Isaka, H. The effect of small topographic variations on reflectance. IEEE Trans. Geosci. Remote Sens. 2002, 40, 663–670. [Google Scholar] [CrossRef]
- Martonchik, J.V.; Bruegge, C.J.; Strahler, A.H. A review of reflectance nomenclature used in remote sensing. Remote Sens. Rev. 2000, 19, 9–20. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.-P.; Yin, T.; Lauret, N.; Cajgfinger, T.; Gregoire, T.; Grau, E.; Feret, J.-B.; Lopes, M.; Guilleux, J.; Dedieu, G.; et al. Discrete anisotropic radiative transfer (DART 5) for modeling airborne and satellite spectroradiometer and LIDAR acquisitions of natural and urban landscapes. Remote Sens. 2015, 7, 1667–1701. [Google Scholar] [CrossRef] [Green Version]
- North, P. Three-dimensional forest light interaction model using a Monte Carlo method. IEEE Trans. Geosci. Remote Sens. 1996, 34, 946–956. [Google Scholar] [CrossRef]
- Vermote, E.F.; Tanre, D.; Deuze, J.L.; Herman, M.; Morcette, J.J. Second simulation of the satellite signal in the solar spectrum, 6S: An overview. IEEE Trans. Geosci. Remote Sens. 1997, 35, 675–686. [Google Scholar] [CrossRef]
- Berk, A.; Conforti, P.; Kennett, R.; Perkins, T.; Hawes, F.; Van Den Bosch, J. MODTRAN6: A major upgrade of the MODTRANradiative transfer code. Proc. SPIE 2014. [Google Scholar] [CrossRef]
- Reese, H.; Olsson, H. C-correction of optical satellite data over alpine vegetation areas: A comparison of sampling strategies for determining the empirical c-parameter. Remote Sens. Environ. 2011, 115, 1387–1400. [Google Scholar] [CrossRef]
- Soenen, S.A.; Peddle, D.R.; Coburn, C.A. SCS + C: A modified sun-canopy-sensor topographic correction in forested terrain. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2148–2159. [Google Scholar] [CrossRef]
- Fan, Y.; Koukal, T.; Weisberg, P.J. A sun–crown–sensor model and adapted c-correction logic for topographic correction of high resolution forest imagery. ISPRS J. Photogramm. Remote Sens. 2014, 96, 94–105. [Google Scholar] [CrossRef]
- Essery, R. Statistical representation of mountain shading. Hydrol. Earth Syst. Sci. 2004, 8, 1047–1052. [Google Scholar] [CrossRef] [Green Version]
- Chen, Y.; Hall, A.; Liou, K.N. Application of three-dimensional solar radiative transfer to mountains. J. Geophys. Res. Atmos. 2006, 111, 5143–5162. [Google Scholar] [CrossRef]
- Richter, R.; Schlaepfer, D. Geo-atmospheric processing of airborne imaging spectrometry data. Part 2: Atmospheric/topographic correction. Int. J. Remote Sens. 2002, 23, 2631–2649. [Google Scholar] [CrossRef]
- Hu, B.; Lucht, W.; Strahler, A.H. The interrelationship of atmospheric correction of reflectances and surface BRDF retrieval: A sensitivity study. IEEE Trans. Geosci. Remote Sens. 1999, 37, 724–738. [Google Scholar]
- Vermote, E.F.; Saleous, N.E.; Justice, C.O.; Kaufman, Y.J.; Privette, J.L.; Remer, L.; Roger, J.C.; Tanré, D. Atmospheric correction of visible to middle-infrared EOS-MODIS data over land surfaces: Background, operational algorithm and validation. J. Geophys. Res. Atmos. 1997, 102, 17131–17141. [Google Scholar] [CrossRef]
- Li, F.; Jupp, D.L.B.; Reddy, S.; Lymburner, L.; Mueller, N.; Tan, P.; Islam, A. An evaluation of the use of atmospheric and BRDF correction to standardize Landsat data. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 257–270. [Google Scholar] [CrossRef]
- Flood, N. Testing the local applicability of MODIS BRDF parameters for correcting Landsat TM imagery. Remote Sens. Lett. 2013, 4, 793–802. [Google Scholar] [CrossRef]
- Verhoef, W.; Bach, H. Coupled soil–leaf-canopy and atmosphere radiative transfer modeling to simulate hyperspectral multi-angular surface reflectance and TOA radiance data. Remote Sens. Environ. 2007, 109, 166–182. [Google Scholar] [CrossRef]
- Li, X.; Strahler, A.H.; Woodcock, C.E. A hybrid geometric optical radiative transfer approach for modeling albedo and directional reflectance of discontinuous canopies. IEEE Trans. Geosci. Remote Sens. 1995, 33, 466–480. [Google Scholar]
- Kuusk, A.; Nilson, T. A directional multispectral forest reflectance model. Remote Sens. Environ. 2000, 72, 244–252. [Google Scholar] [CrossRef]
- Huang, H.G.; Chen, M.; Liu, Q.H.; Liu, Q.A.; Zhang, Y.; Zhao, L.Q.; Qin, W.H.; Zhang, J.; Foody, G.M. A realistic structure model for large-scale surface leaving radiance simulation of forest canopy and accuracy assessment. Int. J. Remote Sens. 2009, 30, 5421–5439. [Google Scholar] [CrossRef]
- Widlowski, J.-L.; Mio, C.; Disney, M.; Adams, J.; Andredakis, I.; Atzberger, C.; Brennan, J.; Busetto, L.; Chelle, M.; Ceccherini, G. The fourth phase of the radiative transfer model intercomparison (RAMI) exercise: Actual canopy scenarios and conformity testing. Remote Sens. Environ. 2015, 169, 418–437. [Google Scholar] [CrossRef]
- Gemmell, F. An investigation of terrain effects on the inversion of a forest reflectance model. Remote Sens. Environ. 1998, 65, 155–169. [Google Scholar] [CrossRef]
- Smith, J.A.; Lin, T.L.; Ranson, K.L. The Lambertian assumption and Landsat data. Photogramm. Eng. Remote Sens. 1980, 46, 1183–1189. [Google Scholar]
- Gu, D.; Gillespie, A. Topographic normalization of Landsat TM images of forest based on subpixel sun–canopy–sensor geometry. Remote Sens. Environ. 1998, 64, 166–175. [Google Scholar] [CrossRef]
- Sandmeier, S.; Itten, K.I. A physically-based model to correct atmospheric and illumination effects in optical satellite data of rugged terrain. IEEE Trans. Geosci. Remote Sens. 1997, 35, 708–717. [Google Scholar] [CrossRef]
- Wen, J.; Liu, Q.; Liu, Q.; Xiao, Q.; Li, X. Parametrized BRDF for atmospheric and topographic correction and albedo estimation in Jiangxi rugged terrain, China. Int. J. Remote Sens. 2009, 30, 2875–2896. [Google Scholar] [CrossRef]
- Lee, W.L.; Liou, K.N.; Hall, A. Parameterization of solar fluxes over mountain surfaces for application to climate models. J. Geophys. Res. Atmos. 2011, 116, 94–104. [Google Scholar] [CrossRef]
- Lefèvre, M.; Oumbe, A.; Blanc, P.; Espinar, B. Mcclear: A new model estimating downwelling solar radiation at ground level in clear-sky conditions. Atmos. Meas. Tech. 2013, 6, 2403–2418. [Google Scholar] [CrossRef] [Green Version]
- Mousivand, A.; Verhoef, W.; Menenti, M.; Gorte, B. Modeling top of atmosphere radiance over heterogeneous non-Lambertian rugged terrain. Remote Sens. 2015, 7, 8019–8044. [Google Scholar] [CrossRef]
- Wu, S.; Wen, J.; Tang, Y.; Zhao, J. Modeling anisotropic bidirectional reflectance of sloping forest. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Fort Worth, TX, USA, 23–28 July 2017; pp. 3874–3877. [Google Scholar]
- Strahler, A.H. Vegetation canopy reflectance modeling—Recent developments and remote sensing perspectives. Remote Sens. Rev. 1997, 15, 179–194. [Google Scholar] [CrossRef]
- Ross, J. Radiative transfer in plant communities. Veg. Atmos. 1975, 1, 13–55. [Google Scholar]
- Cao, B.; Du, Y.; Li, J.; Li, H.; Li, L.; Zhang, Y.; Zou, J.; Liu, Q. Comparison of five slope correction methods for leaf area index estimation from hemispherical photography. IEEE Geosci. Remote Sens. Lett. 2015, 12, 1958–1962. [Google Scholar] [CrossRef]
- Chen, J.M.; Leblanc, S.G. A four-scale bidirectional reflectance model based on canopy architecture. IEEE Trans. Geosci. Remote Sens. 1997, 35, 1316–1337. [Google Scholar] [CrossRef]
- Li, X.; Strahler, A.H. Geometric-optical bidirectional reflectance modeling of the discrete crown vegetation canopy: Effect of crown shape and mutual shadowing. IEEE Trans. Geosci. Remote Sens. 1992, 30, 276–292. [Google Scholar] [CrossRef]
- Ni, W.; Li, X.; Woodcock, C.E.; Caetano, M.R.; Strahler, A.H. An analytical hybrid GORT model for bidirectional reflectance over discontinuous plant canopies. IEEE Trans. Geosci. Remote Sens. 2002, 37, 987–999. [Google Scholar]
- Jin, S.Y.; Susaki, J. A 3-D topographic-relief-correlated Monte Carlo radiative transfer simulator for forest bidirectional reflectance estimation. IEEE Geosci. Remote Sens. Lett. 2017, 14, 964–968. [Google Scholar] [CrossRef]
- Huang, H.; Qin, W.; Liu, Q. RAPID: A radiosity applicable to porous individual objects for directional reflectance over complex vegetated scenes. Remote Sens. Environ. 2013, 132, 221–237. [Google Scholar] [CrossRef]
- Gao, B.; Jia, L.; Menenti, M. An improved method for retrieving land surface albedo over rugged terrain. IEEE Geosci. Remote Sens. Lett. 2014, 11, 554–558. [Google Scholar] [CrossRef]
- Ashdown, I. Radiosity: A Programmer’s Perspective; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 1994; pp. 7–10. [Google Scholar]
- Parviainen, H.; Muinonen, K. Bidirectional reflectance of rough particulate media: Ray-tracing solution. J. Quant. Spectrosc. Radiat. Transf. 2009, 110, 1418–1440. [Google Scholar] [CrossRef]
- Despan, D.; Bedidi, A.; Cervelle, B.; Rudant, J.P. Bidirectional reflectance of Gaussian random surfaces and its scaling properties. Math. Geosci. 1998, 30, 873–888. [Google Scholar]
- Barsky, S.; Petrou, M. The Shadow Function for Rough Surfaces; Kluwer AcaDEMic Publishers: Dordrecht, The Netherlands, 2005; pp. 281–295. [Google Scholar]
- Torrance, K.E.; Sparrow, E.M. Theory for off-specular reflection from roughened surfaces. J. Opt. Soc. Am. 1967, 57, 1105–1114. [Google Scholar] [CrossRef]
- Hapke, B. Theory of Reflectance and Emittance Spectroscopy: Photometric Effects of Large-Scale Roughness; Cambridge University Press: Cambridge, UK, 1993. [Google Scholar]
- Liu, H.; Zhu, J.; Wang, K. Modified polarized geometrical attenuation model for bidirectional reflection distribution function based on random surface microfacet theory. Opt. Express 2015, 23, 22788–22799. [Google Scholar] [CrossRef] [PubMed]
- Blinn, J.F. Models of light reflection for computer synthesized pictures. ACM SIGGRAPH Comput. Graph. 1977, 11, 192–198. [Google Scholar] [CrossRef]
- Buhl, D.; Welch, W.J.; Rea, D.G. Reradiation and thermal emission from illuminated craters on the lunar surface. J. Geophys. Res. 1968, 73, 5281–5295. [Google Scholar] [CrossRef]
- Poulin, P.; Fournier, A. A model for anisotropic reflection. ACM SIGGRAPH Comput. Graph. 1990, 24, 273–282. [Google Scholar] [CrossRef]
- Koenderink, J.J.; Doorn, A.J.V.; Dana, K.J.; Nayar, S. Bidirectional reflection distribution function of thoroughly pitted surfaces. Int. J. Comput. Vis. 1999, 31, 129–144. [Google Scholar] [CrossRef]
- Brockelman, R.; Hagfors, T. Note on the effect of shadowing on the backscattering of waves from a random rough surface. IEEE Trans. Antennas Propag. 1966, 14, 621–626. [Google Scholar] [CrossRef]
- Smith, B. Geometrical shadowing of a random rough surface. IEEE Trans. Antennas Propag. 1967, 15, 668–671. [Google Scholar] [CrossRef]
- Shepard, M.K.; Campbell, B.A. Radar scattering from a self-affine fractal surface: Near-nadir regime. Icarus 1999, 141, 156–171. [Google Scholar] [CrossRef]
- Kelemen, C.; Szirmay-Kalos, L. A microfacet based coupled specular-matte BRDF model with importance sampling. In Proceedings of the Eurographics 2011, Manchester, UK, 3–7 September 2001; pp. 25–34. [Google Scholar]
- Shirley, P.; Smits, B.; Hu, H.; Lafortune, E. A practitioners’ assessment of light reflection models. In Proceedings of the 1997 IEEE the Fifth Pacific Conference on Computer Graphics and Applications, Seoul, Korea, 13–16 October 1997; pp. 40–49. [Google Scholar]
- Deems, J.S.; Fassnacht, S.R.; Elder, K.J. Fractal distribution of snow depth from LIDAR data. J. Hydrometeorol. 2006, 7, 285–297. [Google Scholar] [CrossRef]
- Zhang, X.; Drake, N.A.; Wainwright, J.; Mulligan, M. Comparison of slope estimates from low resolution DEMs: Scaling issues and a fractal method for their solution. Earth Surf. Processes Landf. 2015, 24, 763–779. [Google Scholar] [CrossRef]
- Essery, R. Spatial statistics of wind flow and blowing-snow fluxes over complex topography. Bound.-Layer Meteorol. 2001, 100, 131–147. [Google Scholar] [CrossRef]
- Essery, R.; Marks, D. Scaling and parametrization of clear-sky solar radiation over complex topography. J. Geophys. Res. 2007, 112, 10122. [Google Scholar] [CrossRef]
- Vico, G.; Porporato, A. Probabilistic description of topographic slope and aspect. J. Geophys. Res. Earth Surf. 2009, 114, 441–451. [Google Scholar] [CrossRef]
- Sun, Y. Statistical ray method for deriving reflection models of rough surfaces. J. Opt. Soc. Am. Opt. Image Sci. Vis. 2007, 24, 724–744. [Google Scholar] [CrossRef]
- Beckmann, P. Shadowing of random rough surfaces. IEEE Trans. Antennas Propag. 1965, 13, 384–388. [Google Scholar] [CrossRef]
- Shaw, L.; Beckmann, P. Comments on “shadowing of random surfaces”. IEEE Trans. Antennas Propag. 1966, 14, 253. [Google Scholar] [CrossRef]
- Wagner, R.J. Shadowing of randomly rough surfaces. J. Acoust. Soc. Am. 1967, 41, 138–147. [Google Scholar] [CrossRef]
- Heitz, E.; D’Eon, E.; D’Eon, E.; Dachsbacher, C. Multiple-scattering microfacet BSDFs with the Smith model. ACM Trans. Graph. 2016, 35, 58. [Google Scholar] [CrossRef]
- Bourlier, C.; Saillard, J.; Berginc, G. Effect of correlation between shadowing and shadowed points on the Wagner and Smith monostatic one-dimensional shadowing functions. IEEE Trans. Antennas Propag. 2000, 48, 437–446. [Google Scholar] [CrossRef]
- Bourlier, C.; Berginc, G.; Saillard, J. One- and two-dimensional shadowing functions for any height and slope stationary uncorrelated surface in the monostatic and bistatic configurations. IEEE Trans. Antennas Propag. 2002, 50, 312–324. [Google Scholar] [CrossRef]
- Rexer, M.; Hirt, C. Comparison of free high resolution digital elevation data sets (ASTERGDEM2, SRTM v2.1/v4.1) and validation against accurate heights from the Australian national gravity database. Aust. J. Earth Sci. 2014, 61, 213–226. [Google Scholar] [CrossRef]
- Dozier, J.; Frew, J. Rapid calculation of terrain parameters for radiation modeling from digital elevation data. IEEE Trans. Geosci. Remote Sens. 1990, 28, 963–969. [Google Scholar] [CrossRef]
- Heitz, E. Understanding the masking-shadowing function in microfacet-based BRDFs. J. Comput. Graph. Tech. 2014, 3, 48–107. [Google Scholar]
- Li, F.; Jupp, D.L.B.; Thankappan, M. Issues in the application of digital surface model data to correct the terrain illumination effects in Landsat images. Int. J. Digit. Earth 2015, 8, 235–257. [Google Scholar] [CrossRef]
- Wang, X.; Yin, Z.Y. A comparison of drainage networks derived from digital elevation models at two scales. J. Hydrol. 1998, 210, 221–241. [Google Scholar] [CrossRef]
- Wolock, D.M.; McCabe, G.J. Differences in topographic characteristics computed from 100- and 1000-m resolution digital elevation model data. Hydrol. Processes 2015, 14, 987–1002. [Google Scholar] [CrossRef]
- Yin, Z.Y.; Wang, X. A cross-scale comparison of drainage basin characteristics derived from digital elevation models. Earth Surf. Processes Landf. 2015, 24, 557–562. [Google Scholar] [CrossRef]
- Zhou, Q.; Liu, X. Analysis of errors of derived slope and aspect related to DEM data properties. Comput. Geosci. 2004, 30, 369–378. [Google Scholar] [CrossRef]
- Fleming, M.D.; Hoffer, R.M. Machine Processing of Landsat MSS Data and DMA Topographic Data for Forest Cover Type Mapping; Purdue University: West Lafayette, IN, USA, 1979. [Google Scholar]
- Ritter, P. Vector-based slope and aspect generation algorithm. Am. Soc. Photogramm. Remote Sens. 1987, 53, 1109–1111. [Google Scholar]
- Horn, B.K.P. Hill shading and the reflectance map. IEEE Proc. 1981, 69, 14–47. [Google Scholar] [CrossRef]
- Wood, J. The geomorphological characterisation of digital elevation models. Diss. Theses-Gradworks 1996, 13, 834–848. [Google Scholar]
- Unwin, D.J.; Doomkamp, J.C. Introductory spatial analysis. In Proceedings of the Parallel Problem Solving from Nature—PPSN IV, Berlin, Germany, 22‒26 September 2010; Volume 36, pp. 1307–1319. [Google Scholar]
- Chu, T.H.; Tsai, T.H. Comparison of accuracy and algorithms of slope and aspect measures from DEM. In Proceedings of the GIS AM/FM ASIA’95, Bangkok, Thailand, 21–24 August 1995; pp. 21–24. [Google Scholar]
- Jones, K.H. A comparison of algorithms used to compute hill slope as a property of the DEM. Comput. Geosci. 1998, 24, 315–323. [Google Scholar] [CrossRef]
- Zakšek, K.; Podobnikar, T.; Oštir, K. Solar radiation modelling. Comput. Geosci. 2005, 31, 233–240. [Google Scholar] [CrossRef]
- Helbig, N.; Löwe, H. Parameterization of the spatially averaged sky view factor in complex topography. J. Geophys. Res. Atmos. 2014, 119, 4616–4625. [Google Scholar] [CrossRef]
- Richter, R. Correction of satellite imagery over mountainous terrain. Appl. Opt. 1998, 37, 4004–4015. [Google Scholar] [CrossRef] [PubMed]
- Xin, L.; Koike, T.; Guodong, C. Retrieval of snow reflectance from Landsat data in rugged terrain. Ann. Glaciol. 2002, 34, 31–37. [Google Scholar] [CrossRef]
- Roujean, J.L.; Leroy, M.; Deschamps, P.Y. A bidirectional reflectance model of the earth’s surface for the correction of remote sensing data. J. Geophys. Res. Atmos. 1992, 97, 20455–20468. [Google Scholar] [CrossRef]
- Wanner, W.; Li, X.; Strahler, A.H. On the derivation of kernels for kernel-driven models of bidirectional reflectance. J. Geophys. Res. Atmos. 1995, 100, 21077–21089. [Google Scholar] [CrossRef]
- Bruegge, C.; Chrien, N.; Haner, D. A spectralon BRF data base for MISR calibration applications. Remote Sens. Environ. 2001, 77, 354–366. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.P.; Guillevic, P.; Zagolski, F.; DEMarez, V.; Trichon, V.; Deering, D.; Leroy, M. Modeling BRF and radiation regime of boreal and tropical forests: I. BRF. Remote Sens. Environ. 1999, 68, 281–316. [Google Scholar] [CrossRef]
- Liu, S.; Liu, Q.; Liu, Q.; Wen, J.; Li, X.; Xiao, Q.; Xin, X. The angular & spectral kernel model for BRDF and albedo retrieval. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2010, 3, 241–256. [Google Scholar]
- You, D.; Wen, J.; Liu, Q.; Liu, Q.; Tang, Y. The angular and spectral kernel-driven model: Assessment and application. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 1331–1345. [Google Scholar]
- Wen, J.; Dou, B.; You, D.; Tang, Y.; Xiao, Q.; Liu, Q.; Liu, Q. Forward a small-timescale BRDF/albedo by multisensor combined BRDF inversion model. IEEE Trans. Geosci. Remote Sens. 2017, 55, 683–697. [Google Scholar] [CrossRef]
- Huang, H.; Qin, W.; Spurr, R.J.D.; Liu, Q. Evaluation of atmospheric effects on land-surface directional reflectance with the coupled RAPID and VLIDORT models. IEEE Geosci. Remote Sens. Lett. 2017, 14, 916–920. [Google Scholar] [CrossRef]















| Model Category | Model Name | Geometry Correction | Tree’s Negative Geotropism | Diffuse Irradiance | Typical Reference |
|---|---|---|---|---|---|
| Radiative transfer | ROSST | √ | √ | × | Combal et al. [27] |
| PLC | √ | √ | √ | Yin et al. [20] | |
| Geometric optical | GOMST | √ | × | × | Schaaf et al. [21] |
| GOST1 | √ | √ | × | Fan et al. [17] | |
| Hybrid | SLCT | √ | × | √ | Mousivand et al. [64] |
| GOST2 | √ | √ | × | Fan et al. [24] | |
| GOSAILT | √ | √ | √ | Wu et al. [65] |
| Type | Terrain Description | Interior Topography Characteristics | Typical Reference |
|---|---|---|---|
| Special-shape | V-cavity | The surface consists of small symmetrical or non-symmetrical V-cavities | Torrance et al. [79]; Liu et al. [81]; Blinn et al. [82] |
| Sphere-cavity | The surface consists of periodical positive sphere-cavities or negative sphere-cavities. | Buhlet al. [83]; Poulin et al. [84]; Koenderink et al. [85] | |
| Random field | Random distribution | The height or the slope conforms to the Gaussian normal distribution, the exponential distribution, or other random distributions | Despan et al. [77]; Hapke [80]; Brockelman et al. [86]; Smith [87] |
| Fractal | Describes the dependence of surface roughness on scale by a power law | Barsky et al. [78]; Shepard et al. [88] | |
| DEM | DEM | The terrain is described by high spatial resolution digital elevation models | Wen et al. [29]; Roupioz et al. [31] |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wen, J.; Liu, Q.; Xiao, Q.; Liu, Q.; You, D.; Hao, D.; Wu, S.; Lin, X. Characterizing Land Surface Anisotropic Reflectance over Rugged Terrain: A Review of Concepts and Recent Developments. Remote Sens. 2018, 10, 370. https://doi.org/10.3390/rs10030370
Wen J, Liu Q, Xiao Q, Liu Q, You D, Hao D, Wu S, Lin X. Characterizing Land Surface Anisotropic Reflectance over Rugged Terrain: A Review of Concepts and Recent Developments. Remote Sensing. 2018; 10(3):370. https://doi.org/10.3390/rs10030370
Chicago/Turabian StyleWen, Jianguang, Qiang Liu, Qing Xiao, Qinhuo Liu, Dongqin You, Dalei Hao, Shengbiao Wu, and Xingwen Lin. 2018. "Characterizing Land Surface Anisotropic Reflectance over Rugged Terrain: A Review of Concepts and Recent Developments" Remote Sensing 10, no. 3: 370. https://doi.org/10.3390/rs10030370
APA StyleWen, J., Liu, Q., Xiao, Q., Liu, Q., You, D., Hao, D., Wu, S., & Lin, X. (2018). Characterizing Land Surface Anisotropic Reflectance over Rugged Terrain: A Review of Concepts and Recent Developments. Remote Sensing, 10(3), 370. https://doi.org/10.3390/rs10030370