Estimation of Daily Average Downward Shortwave Radiation over Antarctica
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data
2.1.1. Cloud Data and Instantaneous Irradiance Data
2.1.2. Ground Station Data
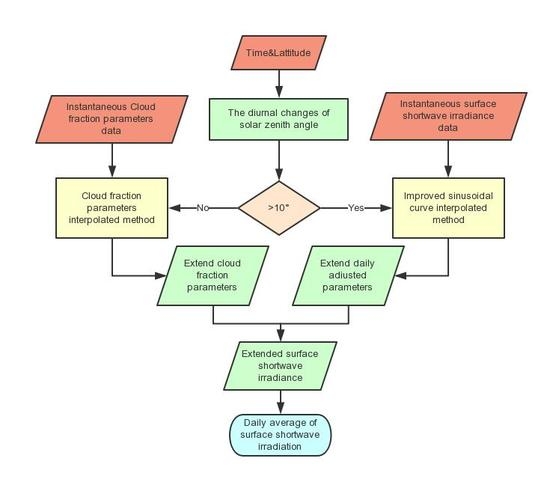
2.2. Temporal Scaling-Up Method
2.2.1. Calculation of the Diurnal Variation Range of SZA
2.2.2. Improved Sinusoidal Method
2.2.3. Cloud Coverage Fraction Interpolated Method
2.2.4. Modelling Daily Solar Radiation
3. Results
3.1. Diurnal Variation in SZA
3.2. Diurnal Cycle of Interpolated Irradiance at Different Stations
3.3. Average Daily Irradiation at Different Stations
4. Discussion
4.1. Comparison of the Algorithm of the National Aeronautics and Space Administration (NASA)’s Surface Solar Radiation Budget Data Set
4.2. Comparison with Traditional Interpolation Methods
4.3. Limitation and Further Study
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A


| Main Input Parameter | Description | Unit |
|---|---|---|
| SZA | solar zenith angle | ° |
| Albedo | surface albedo | - |
| VIS | visibility | km |
| COT | cloud optical thickness | - |
| CBH | cloud base height | km |
| Alt | altitude | km |
| HECF | hemispheric cloud fraction | - |
| RCF | regional cloud fraction | - |
References
- Platt, T. Primary production of the ocean water column as a function of surface light intensity: Algorithms for remote sensing. Deep Sea Res. Part A Oceanogr. Res. Pap. 1986, 33, 149–163. [Google Scholar] [CrossRef]
- Shook, K.; Pomeroy, J. Synthesis of incoming shortwave radiation for hydrological simulation. Hydrol. Res. 2011, 42, 433–446. [Google Scholar] [CrossRef]
- Wild, M.; Ohmura, A.; Schär, C.; Müller, G.; Folini, D.; Schwarz, M.; Hakuba, M.Z.; Sanchez-Lorenzo, A. The global energy balance archive (GEBA) version 2017: A database for worldwide measured surface energy fluxes. Earth Syst. Sci. Data 2017, 9, 601. [Google Scholar] [CrossRef]
- Budyko, M.I. The effect of solar radiation variations on the climate of the earth. Tellus 1969, 21, 611–619. [Google Scholar] [CrossRef]
- Kiehl, J.T.; Trenberth, K.E. Earth’s annual global mean energy budget. Bull. Am. Meteorol. Soc. 1997, 78, 197–208. [Google Scholar] [CrossRef]
- Foukal, P.; Fröhlich, C.; Spruit, H.; Wigley, T. Variations in solar luminosity and their effect on the earth’s climate. Nature 2006, 443, 161–166. [Google Scholar] [CrossRef] [PubMed]
- Hansom, J.D.; Gordon, J. Antarctic Environments and Resources: A Geographical Perspective; Routledge: New York, NY, USA; Oxfordshire, UK, 2014. [Google Scholar]
- Hall, A. The role of surface albedo feedback in climate. J. Clim. 2004, 17, 1550–1568. [Google Scholar] [CrossRef]
- Holland, M.M.; Bitz, C.M. Polar amplification of climate change in coupled models. Clim. Dyn. 2003, 21, 221–232. [Google Scholar] [CrossRef]
- Stanhill, G.; Cohen, S. Recent changes in solar irradiance in Antarctica. J. Clim. 1997, 10, 2078–2086. [Google Scholar] [CrossRef]
- King, J.; Connolley, W. Validation of the surface energy balance over the antarctic ice sheets in the UK meteorological office unified climate model. J. Clim. 1997, 10, 1273–1287. [Google Scholar] [CrossRef]
- Stocker, T. Climate Change 2013: The Physical Science Basis: Working Group I Contribution to the Fifth Assessment Report of the Intergovernmental Panel on Climate Change; Cambridge University Press: Cambridge, UK, 2014. [Google Scholar]
- Wild, M.; Folini, D.; Henschel, F.; Fischer, N.; Müller, B. Projections of long-term changes in solar radiation based on cmip5 climate models and their influence on energy yields of photovoltaic systems. Sol. Energy 2015, 116, 12–24. [Google Scholar] [CrossRef]
- Trnka, M.; Žalud, Z.; Eitzinger, J.; Dubrovský, M. Global solar radiation in central European lowlands estimated by various empirical formulae. Agric. For. Meteorol. 2005, 131, 54–76. [Google Scholar] [CrossRef]
- Journée, M.; Bertrand, C. Improving the spatio-temporal distribution of surface solar radiation data by merging ground and satellite measurements. Remote Sens. Environ. 2010, 114, 2692–2704. [Google Scholar] [CrossRef]
- Pinker, R.; Frouin, R.; Li, Z. A review of satellite methods to derive surface shortwave irradiance. Remote Sens. Environ. 1995, 51, 108–124. [Google Scholar] [CrossRef]
- Liang, S.; Zheng, T.; Liu, R.; Fang, H.; Tsay, S.C.; Running, S. Estimation of incident photosynthetically active radiation from moderate resolution imaging spectrometer data. J. Geophys. Res. Atmos. 2006, 111. [Google Scholar] [CrossRef]
- Bisht, G.; Venturini, V.; Islam, S.; Jiang, L. Estimation of the net radiation using modis (moderate resolution imaging spectroradiometer) data for clear sky days. Remote Sens. Environ. 2005, 97, 52–67. [Google Scholar] [CrossRef]
- Tarpley, J. Estimating incident solar radiation at the surface from geostationary satellite data. J. Appl. Meteorol. 1979, 18, 1172–1181. [Google Scholar] [CrossRef]
- Lagouarde, J.; Brunet, Y. A simple model for estimating the daily upward longwave surface radiation flux from noaa-avhrr data. Int. J. Remote Sens. 1993, 14, 907–925. [Google Scholar] [CrossRef]
- Van Laake, P.E.; Sanchez-Azofeifa, G.A. Mapping par using modis atmosphere products. Remote Sens. Environ. 2005, 94, 554–563. [Google Scholar] [CrossRef]
- Niu, X. Radiative Fluxes and Albedo Feedback in Polar Regions; University of Maryland: College Park, MD, USA, 2011. [Google Scholar]
- Wang, D.; Liang, S.; Liu, R.; Zheng, T. Estimation of daily-integrated par from sparse satellite observations: Comparison of temporal scaling methods. Int. J. Remote Sens. 2010, 31, 1661–1677. [Google Scholar] [CrossRef]
- Xu, X.; Du, H.; Zhou, G.; Mao, F.; Li, P.; Fan, W.; Zhu, D. A method for daily global solar radiation estimation from two instantaneous values using modis atmospheric products. Energy 2016, 111, 117–125. [Google Scholar] [CrossRef]
- Chen, L.; Yan, G.; Ren, H.; Wang, T. A simple fusion algorithm of polar-orbiting and geostationary satellite data for the estimation of surface shortwave fluxes. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; IEEE: Piscataway, NJ, USA, 2016; pp. 2657–2660. [Google Scholar]
- Cao, C.; De Luccia, F.J.; Xiong, X.; Wolfe, R.; Weng, F. Early on-orbit performance of the visible infrared imaging radiometer suite onboard the suomi national polar-orbiting partnership (s-npp) satellite. IEEE Trans. Geosci. Remote Sens. 2014, 52, 1142–1156. [Google Scholar] [CrossRef]
- Yan, K.; Park, T.; Chen, C.; Xu, B.; Song, W.; Yang, B.; Zeng, Y.; Liu, Z.; Yan, G.; Knyazikhin, Y.; et al. Generating global products of lai and fpar from snpp-viirs data: Theoretical background and implementation. IEEE Trans. Geosci. Remote Sens. 2018, PP, 1–19. [Google Scholar] [CrossRef]
- Zhao, J.; Yan, G.; Jiao, Z.; Chen, L.; Chu, Q. Enhanced shortwave radiative transfer model based on sbdart. J. Remote Sens. 2017, 6, 853–863. [Google Scholar]
- König-Langlo, G.; Sieger, R.; Schmithüsen, H.; Bücker, A.; Richter, F.; Dutton, E. The Baseline Surface Radiation Network and Its World Radiation Monitoring Centre at the Alfred Wegener Institute; World Meteorological Organization: Geneva, Switzerland, 2013. [Google Scholar]
- König-Langlo, G.; Loose, B. The meteorological observatory at neumayer stations (gvn and nm-ii) Antarctica. Polarforschung2006 2007, 76, 25–38. [Google Scholar]
- Dutton, E.G. Basic and other measurements of radiation at station south pole (1998-06). Earth Environ. Sci. 2007. [Google Scholar] [CrossRef]
- Grena, R. An algorithm for the computation of the solar position. Sol. Energy 2008, 82, 462–470. [Google Scholar] [CrossRef]
- Chen, L.; Yan, G.; Wang, T.; Ren, H.; Calbó, J.; Zhao, J.; McKenzie, R. Estimation of surface shortwave radiation components under all sky conditions: Modeling and sensitivity analysis. Remote Sens. Environ. 2012, 123, 457–469. [Google Scholar] [CrossRef]
- Gueymard, C.A. A review of validation methodologies and statistical performance indicators for modeled solar radiation data: Towards a better bankability of solar projects. Renew. Sustain. Energy Rev. 2014, 39, 1024–1034. [Google Scholar] [CrossRef]
- Román, R.; Antón, M.; Valenzuela, A.; Gil, J.; Lyamani, H.; De Miguel, A.; Olmo, F.; Bilbao, J.; Alados-Arboledas, L. Evaluation of the desert dust effects on global, direct and diffuse spectral ultraviolet irradiance. Tellus B Chem. Phys. Meteorol. 2013, 65, 19578. [Google Scholar] [CrossRef]
- Mateos, D.; Bilbao, J.; Kudish, A.; Parisi, A.; Carbajal, G.; Di Sarra, A.; Román, R.; De Miguel, A. Validation of omi satellite erythemal daily dose retrievals using ground-based measurements from fourteen stations. Remote Sens. Environ. 2013, 128, 1–10. [Google Scholar] [CrossRef] [Green Version]
- De Miguel-Bilbao, S.; Ramos, V.; Blas, J. Assessment of polarization dependence of body shadow effect on dosimetry measurements in 2.4 ghz band. Bioelectromagnetics 2017, 38, 315–321. [Google Scholar] [CrossRef] [PubMed]
- Pinker, R.; Laszlo, I. Modeling surface solar irradiance for satellite applications on a global scale. J. Appl. Meteorol. 1992, 31, 194–211. [Google Scholar] [CrossRef]
- Gupta, S.K.; Kratz, D.P.; Stackhouse, P.W., Jr.; Wilber, A.C. The Langley Parameterized Shortwave Algorithm (LPSA) for Surface Radiation Budget Studies; version 1.0; Langley Research Center: Hampton, VA, USA, 2001.
- Yang, J.; Zhang, Z.; Wei, C.; Lu, F.; Guo, Q. Introducing the new generation of Chinese geostationary weather satellites–fengyun 4 (fy-4). Bull. Am. Meteorol. Soc. 2016. [CrossRef]
- Bessho, K.; Date, K.; Hayashi, M.; Ikeda, A.; Imai, T.; Inoue, H.; Kumagai, Y.; Miyakawa, T.; Murata, H.; Ohno, T. An introduction to himawari-8/9—Japan’s new-generation geostationary meteorological satellites. J. Meteorol. Soc. Jpn. Ser. II 2016, 94, 151–183. [Google Scholar] [CrossRef]
- Yan, G.; Wang, T.; Jiao, Z.; Mu, X.; Zhao, J.; Chen, L. Topographic radiation modeling and spatial scaling of clear-sky land surface longwave radiation over rugged terrain. Remote Sens. Environ. 2016, 172, 15–27. [Google Scholar] [CrossRef]
- Jiao, Z.; Yan, G.; Zhao, J.; Wang, T.; Chen, L. Estimation of surface upward longwave radiation from modis and viirs clear-sky data in the Tibetan plateau. Remote Sens. Environ. 2015, 162, 221–237. [Google Scholar] [CrossRef]








| Station Name | Abbreviation | Latitude | Longitude | Elevation (m) | Surface Condition |
|---|---|---|---|---|---|
| Georg von Neumayer | GVN | 70.65°S | 8.25°W | 42 | Ice sheet |
| South Pole | SPO | 89.98°S | 24.80°W | 2800 | Glaciers and deposits |
| Station | Method | R2 | C1 (W/m2) | C2 | RMSE (W/m2) | RMSE (%) | MBE (W/m2) | MBE (%) |
|---|---|---|---|---|---|---|---|---|
| GVN station | Improved sinusoidal curve | 0.93 | 35.49 | 0.95 | 32.21 | 8.52 | 17.77 | 4.70 |
| Traditional sinusoidal curve | 0.68 | 55.50 | 1.09 | 70.32 | 18.59 | 36.39 | 9.62 | |
| SPO station | Cloud coverage fraction Interpolation | 0.96 | 13.97 | 0.96 | 25.27 | 6.98 | 0.32 | 0.08 |
| Linear interpolation | 0.79 | 28.51 | 1.04 | 57.40 | 15.87 | 30.18 | 8.34 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Zhou, Y.; Yan, G.; Zhao, J.; Chu, Q.; Liu, Y.; Yan, K.; Tong, Y.; Mu, X.; Xie, D.; Zhang, W. Estimation of Daily Average Downward Shortwave Radiation over Antarctica. Remote Sens. 2018, 10, 422. https://doi.org/10.3390/rs10030422
Zhou Y, Yan G, Zhao J, Chu Q, Liu Y, Yan K, Tong Y, Mu X, Xie D, Zhang W. Estimation of Daily Average Downward Shortwave Radiation over Antarctica. Remote Sensing. 2018; 10(3):422. https://doi.org/10.3390/rs10030422
Chicago/Turabian StyleZhou, Yingji, Guangjian Yan, Jing Zhao, Qing Chu, Yanan Liu, Kai Yan, Yiyi Tong, Xihan Mu, Donghui Xie, and Wuming Zhang. 2018. "Estimation of Daily Average Downward Shortwave Radiation over Antarctica" Remote Sensing 10, no. 3: 422. https://doi.org/10.3390/rs10030422
APA StyleZhou, Y., Yan, G., Zhao, J., Chu, Q., Liu, Y., Yan, K., Tong, Y., Mu, X., Xie, D., & Zhang, W. (2018). Estimation of Daily Average Downward Shortwave Radiation over Antarctica. Remote Sensing, 10(3), 422. https://doi.org/10.3390/rs10030422