Spatio-Temporal Variability of Annual Sea Level Cycle in the Baltic Sea
Abstract
:1. Introduction
2. Data
2.1. Satellite Altimetry Data
2.2. Tide Gauge Data
2.3. Model Reanalysis
2.4. Assessment of Altimetry and Model Reanalysis
3. Method
4. Results
4.1. Temporal and Spatial Variability of the Annual Sea Level Cycle
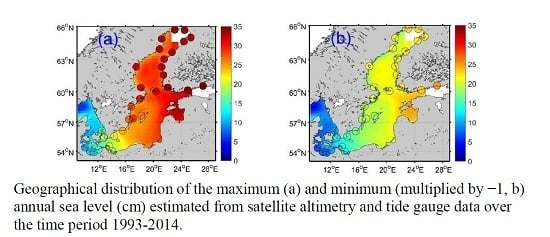
4.2. Extreme Annual Sea Level Cycle
4.3. Relations between Annual Sea Level and Atmospheric Parameters
4.3.1. Wind Speed
4.3.2. NAO Index
4.3.3. Sea Level Pressure
4.3.4. Air Temperature
5. Discussion
6. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
Appendix A

References
- Jaagus, J.; Suursaar, Ü. Long-term storminess and sea level variations on the estonian coast of the Baltic Sea in relation to large-scale atmospheric circulation. Estonian J. Earth Sci. 2013, 62, 73–92. [Google Scholar] [CrossRef]
- Madsen, K.S.; Høyer, J.L.; Fu, W.; Donlon, C. Blending of satellite and tide gauge sea level observations and its assimilation in a storm surge model of the North Sea and Baltic Sea. J. Geophys. Res. Oceans 2015, 120, 6405–6418. [Google Scholar] [CrossRef]
- Xu, Q.; Cheng, Y.; Plag, H.-P.; Zhang, B. Investigation of sea level variability in the Baltic Sea from tide gauge, satellite altimeter data, and model reanalysis. Int. J. Remote Sens. 2015, 36, 2548–2568. [Google Scholar] [CrossRef]
- Cheng, Y.; Andersen, O.B.; Knudsen, P.; Xu, Q. Multimission Satellite Altimetric Data Validation in the Baltic Sea. In Proceedings of the 2014 IEEE Geoscience and Remote Sensing Symposium, Quebec City, QC, Canada, 13–18 July 2014; pp. 4536–4539. [Google Scholar]
- Han, G.; Loder, J.; Petrie, B. Tidal and non-tidal sea level variability along the coastal nova scotia from satellite altimetry. Int. J. Remote Sens. 2010, 31, 4791–4806. [Google Scholar] [CrossRef]
- Han, G. Sea level and surface current variability in the Gulf of St Lawrence from satellite altimetry. Int. J. Remote Sens. 2004, 25, 5069–5088. [Google Scholar] [CrossRef]
- Feng, X.; Tsimplis, M.N.; Marcos, M.; Calafat, F.M.; Zheng, J.; Jordà, G.; Cipollini, P. Spatial and temporal variations of the seasonal sea level cycle in the Northwest Pacific. J. Geophys. Res. Oceans 2015, 120, 7091–7112. [Google Scholar] [CrossRef]
- Handoko, E.; Fernandes, M.; Lázaro, C. Assessment of altimetric range and geophysical corrections and mean sea surface models—Impacts on sea level variability around the Indonesian seas. Remote Sens. 2017, 9, 102. [Google Scholar] [CrossRef]
- Bosch, W.; Dettmering, D.; Schwatke, C. Multi-mission cross-calibration of satellite altimeters: Constructing a long-term data record for global and regional sea level change studies. Remote Sens. 2014, 6, 2255–2281. [Google Scholar] [CrossRef]
- Hünicke, B.; Zorita, E. Trends in the amplitude of Baltic Sea level annual cycle. Tellus A 2008, 60, 154–164. [Google Scholar] [CrossRef]
- Stramska, M.; Kowalewska-Kalkowska, H.; Świrgoń, M. Seasonal variability in the Baltic Sea level. Oceanologia 2013, 55, 787–807. [Google Scholar] [CrossRef]
- Etcheverry, L.R.; Saraceno, M.; Piola, A.R.; Valladeau, G.; Möller, O. A comparison of the annual cycle of sea level in coastal areas from gridded satellite altimetry and tide gauges. Cont. Shelf Res. 2015, 92, 87–97. [Google Scholar] [CrossRef]
- Medvedev, I. Seasonal fluctuations of the Baltic Sea level. Russ. Meteorol. Hydrol. 2014, 39, 814–822. [Google Scholar] [CrossRef]
- Barbosa, S.M.; Donner, R.V. Long-term changes in the seasonality of Baltic Sea level. Tellus A 2016, 68, 30540. [Google Scholar] [CrossRef]
- Cheng, Y.; Hamlington, B.; Plag, H.-P.; Xu, Q. Influence of enso on the variation of annual sea level cycle in the south china sea. Ocean Eng. 2016, 126, 343–352. [Google Scholar] [CrossRef]
- Cheng, Y.; Plag, H.-P.; Hamlington, B.D.; Xu, Q.; He, Y. Regional sea level variability in the bohai sea, yellow sea, and east china sea. Cont. Shelf Res. 2015, 111, 95–107. [Google Scholar] [CrossRef]
- Kim, K.-Y.; Wu, Q. A comparison study of eof techniques: Analysis of nonstationary data with periodic statistics. J. Clim. 1999, 12, 185–199. [Google Scholar] [CrossRef]
- Hamlington, B.; Leben, R.; Nerem, R.; Kim, K.-Y. The effect of signal-to-noise ratio on the study of sea level trends. J. Clim. 2011, 24, 1396–1408. [Google Scholar] [CrossRef]
- Kim, K.-Y.; Hamlington, B.; Na, H. Theoretical foundation of cyclostationary eof analysis for geophysical and climatic variables: Concepts and examples. Earth Sci. Rev. 2015, 150, 201–218. [Google Scholar] [CrossRef]
- Høyer, J.L.; Karagali, I. Sea surface temperature climate data record for the North Sea and Baltic Sea. J. Clim. 2016, 29, 2529–2541. [Google Scholar] [CrossRef]
- Lehmann, A.; Getzlaff, K.; Harlaß, J. Detailed assessment of climate variability of the Baltic Sea area for the period 1958–2009. Clim. Res. 2011, 46, 185–196. [Google Scholar] [CrossRef]
- Rio, M.H.; Pascual, A.; Poulain, P.M.; Menna, M.; Barceló, B.; Tintoré, J. Computation of a new mean dynamic topography for the mediterranean sea from model outputs, altimeter measurements and oceanographic in-situ data. Ocean Sci. Discuss. 2014, 11, 655–692. [Google Scholar] [CrossRef]
- Cheng, X.; McCreary, J.P.; Qiu, B.; Qi, Y.; Du, Y. Intraseasonal-to-semiannual variability of sea-surface height in the astern, equatorial Indian Ocean and southern bay of bengal. J. Geophys. Res. Oceans 2017, 122, 4051–4067. [Google Scholar] [CrossRef]
- Holgate, S.J.; Matthews, A.; Woodworth, P.L.; Rickards, L.J.; Tamisiea, M.E.; Bradshaw, E.; Foden, P.R.; Gordon, K.M.; Jevrejeva, S.; Pugh, J. New data systems and products at the permanent service for mean sea level. J. Coast. Res. 2013, 29, 493–504. [Google Scholar] [CrossRef]
- Kim, K.-Y.; North, G.R. Eofs of harmonizable cyclostationary processes. J. Atmos. Sci. 1997, 54, 2416–2427. [Google Scholar] [CrossRef]
- Passaro, M.; Cipollini, P.; Benveniste, J. Annual sea level variability of the coastal ocean: The Baltic Sea-North Sea transition zone. J. Geophys. Res. Oceans 2015, 120, 3061–3078. [Google Scholar] [CrossRef]
- Wolski, T.; Wiśniewski, B.; Giza, A.; Kowalewska-Kalkowska, H.; Boman, H.; Grabbi-Kaiv, S.; Hammarklint, T.; Holfort, J.; Lydeikaitė, Ž. Extreme sea levels at selected stations on the Baltic Sea coast. Oceanologia 2014, 56, 259–290. [Google Scholar] [CrossRef]
- Andersson, H.C. Influence of long-term regional and large-scale atmospheric circulation on the Baltic Sea level. Tellus A 2002, 54, 76–88. [Google Scholar] [CrossRef]
- Jevrejeva, S.; Moore, J.; Woodworth, P.; Grinsted, A. Influence of large-scale atmospheric circulation on European Sea level: Results based on the wavelet transform method. Tellus A 2005, 57, 183–193. [Google Scholar] [CrossRef]
- Compo, G.P.; Whitaker, J.S.; Sardeshmukh, P.D.; Matsui, N.; Allan, R.J.; Yin, X.; Gleason, B.E.; Vose, R.S.; Rutledge, G.; Bessemoulin, P.; et al. The twentieth century reanalysis project. Q. J. R. Meteorol. Soc. 2011, 137, 1–28. [Google Scholar] [CrossRef]
- Stramska, M.; Chudziak, N. Recent multiyear trends in the Baltic Sea level. Oceanologia 2013, 55, 319–337. [Google Scholar] [CrossRef]
- Hurrell, J.W. Decadal trends in the north atlantic oscillation: Regional temperatures and precipitation. Science 1995, 269, 676–679. [Google Scholar] [CrossRef] [PubMed]
- Kalnay, E.; Kanamitsu, M.; Kistler, R.; Collins, W.; Deaven, D.; Gandin, L.; Iredell, M.; Saha, S.; White, G.; Woollen, J. The NCEP/NCAR 40-year reanalysis project. Bull. Am. Meteorol. Soc. 1996, 77, 437–471. [Google Scholar] [CrossRef]
- Cipollini, P.; Calafat, F.M.; Jevrejeva, S.; Melet, A.; Prandi, P. Monitoring sea level in the coastal zone with satellite altimetry and tide gauges. Surv. Geophys. 2017, 38, 33–57. [Google Scholar] [CrossRef]



















| Tide Gauge | Latitude (°N) | Longitude (°E) | Data Availability (%, 1993–2014) | |
|---|---|---|---|---|
| 1 | WISMAR † | 53.900 | 11.458 | 100.00 |
| 2 | WARNEMUNDE † | 54.170 | 12.103 | 100.00 |
| 3 | TRAVEMUNDE | 53.958 | 10.872 | 100.00 |
| 4 | HELSINKI † | 60.154 | 24.956 | 99.62 |
| 5 | VAASA | 63.082 | 21.571 | 89.39 |
| 6 | OLANDS NORRA UDDE † | 57.366 | 17.097 | 100.00 |
| 7 | KUNGSHOLMSFORT † | 56.105 | 15.589 | 100.00 |
| 8 | STOCKHOLM † | 59.324 | 18.082 | 100.00 |
| 9 | OULU | 65.040 | 25.418 | 100.00 |
| 10 | FREDERICIA * | 55.561 | 9.754 | 90.91 |
| 11 | KOBENHAVN * | 55.705 | 12.600 | 86.36 |
| 12 | RATAN † | 63.986 | 20.895 | 100.00 |
| 13 | SLIPSHAVN * | 55.288 | 10.828 | 86.74 |
| 14 | KORSOR * | 55.332 | 11.142 | 90.53 |
| 15 | KLAIPEDA ♦ | 55.700 | 21.133 | 83.71 |
| 16 | HORNBAEK *,† | 56.091 | 12.458 | 89.77 |
| 17 | GEDSER *,† | 54.573 | 11.926 | 90.53 |
| 18 | MANTYLUOTO | 61.594 | 21.463 | 99.62 |
| 19 | PIETARSAARI | 63.709 | 22.690 | 98.86 |
| 20 | FURUOGRUND | 64.916 | 21.231 | 98.11 |
| 21 | KEMI | 65.673 | 24.515 | 100.00 |
| 22 | TURKU | 60.428 | 22.101 | 100.00 |
| 23 | RAAHE | 64.666 | 24.407 | 100.00 |
| 24 | FOGLO | 60.032 | 20.385 | 100.00 |
| 25 | KASKINEN | 62.344 | 21.215 | 100.00 |
| 26 | HAMINA | 60.563 | 27.179 | 99.62 |
| 27 | KLAGSHAMN | 55.522 | 12.894 | 100.00 |
| 28 | SASSNITZ | 54.511 | 13.643 | 100.00 |
| 29 | RODBYHAVN * | 54.656 | 11.349 | 90.91 |
| 30 | KIEL | 54.372 | 10.157 | 100.00 |
| 31 | SPIKARNA | 62.363 | 17.531 | 99.62 |
| 32 | KOSEROW | 54.060 | 14.000 | 98.11 |
| 33 | TEJN * | 55.250 | 14.838 | 89.77 |
| 34 | KALIX | 65.697 | 23.096 | 98.86 |
| 35 | SKAGSUDDE ** | 63.191 | 19.013 | 94.32 |
| 36 | FORSMARK | 60.409 | 18.211 | 100.00 |
| 37 | MARVIKEN | 58.554 | 16.837 | 100.00 |
| 38 | VISBY | 57.639 | 18.284 | 100.00 |
| 39 | OSKARSHAMN | 57.275 | 16.478 | 100.00 |
| 40 | SIMRISHAMN | 55.557 | 14.358 | 100.00 |
| 41 | SKANOR | 55.417 | 12.829 | 100.00 |
| 42 | VIKEN | 56.142 | 12.579 | 100.00 |
| WIS | WAR | GED | HOR | KUN | OLA | STO | HEL | RAT | |
|---|---|---|---|---|---|---|---|---|---|
| U-wind | 0.6 ± 0.0 | 0.7 ± 0.0 | 0.6 ± 0.0 | 0.6 ± 0.0 | 0.6 ± 0.0 | 0.5 ± 0.0 | 0.6 ± 0.0 | 0.7 ± 0.0 | 0.5 ± 0.0 |
| NAO | 0.1 ± 0.1 | 0.2 ± 0.1 | 0.1 ± 0.1 | 0.2 ± 0.1 | 0.3 ± 0.1 | 0.2 ± 0.1 | 0.3 ± 0.1 | 0.3 ± 0.1 | 0.2 ± 0.1 |
| Winter-NAO | 0.4 ± 0.2 | 0.4 ± 0.2 | 0.4 ± 0.2 | 0.5 ± 0.1 | 0.6 ± 0.1 | 0.5 ± 0.1 | 0.6 ± 0.1 | 0.6 ± 0.1 | 0.5 ± 0.1 |
| Air-t | −0.2 ± 0.1 | −0.2 ± 0.1 | −0.1 ± 0.1 | −0.0 ± 0.1 | −0.0 ± 0.1 | 0.0 ± 0.1 | 0.0 ± 0.1 | −0.0 ± 0.1 | 0.0 ± 0.1 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Cheng, Y.; Xu, Q.; Li, X. Spatio-Temporal Variability of Annual Sea Level Cycle in the Baltic Sea. Remote Sens. 2018, 10, 528. https://doi.org/10.3390/rs10040528
Cheng Y, Xu Q, Li X. Spatio-Temporal Variability of Annual Sea Level Cycle in the Baltic Sea. Remote Sensing. 2018; 10(4):528. https://doi.org/10.3390/rs10040528
Chicago/Turabian StyleCheng, Yongcun, Qing Xu, and Xiaofeng Li. 2018. "Spatio-Temporal Variability of Annual Sea Level Cycle in the Baltic Sea" Remote Sensing 10, no. 4: 528. https://doi.org/10.3390/rs10040528
APA StyleCheng, Y., Xu, Q., & Li, X. (2018). Spatio-Temporal Variability of Annual Sea Level Cycle in the Baltic Sea. Remote Sensing, 10(4), 528. https://doi.org/10.3390/rs10040528