Comparing Terrestrial Laser Scanning (TLS) and Wearable Laser Scanning (WLS) for Individual Tree Modeling at Plot Level

Abstract

This study presents a comparison between the use of wearable laser scanning (WLS) and terrestrial laser scanning (TLS) devices for automatic tree detection with an estimation of two dendrometric variables: diameter at breast height (DBH) and total tree height (TH). Operative processes for data collection and automatic forest inventory are described in detail. The approach used is based on the clustering of points belonging to each individual tree, the isolation of the trunks, the iterative fitting of circles for the DBH calculation and the computation of the TH of each tree. TLS and WLS point clouds were compared by the statistical analysis of both estimated forest dendrometric parameters and the possible presence of bias. Results show that the apparent differences in point density and relative precision between both 3D forest models do not affect tree detection and DBH estimation. Nevertheless, tree height estimation using WLS appears to be affected by the limited scanning range of the WLS used in this study. TH estimations for trees below a certain height are equivalent using WLS or TLS, whereas TH of taller trees is clearly underestimated using WLS.

1. Introduction

Forest inventory is necessary to estimate the forest resources in a region or even a country and to plan their maintenance and efficient exploitation. On a large scale, forest inventory can be achieved using airborne laser scanning (ALS) data combined with field sampling. A large number of methods and case studies concerning this topic can be found in the literature [1,2,3,4,5,6,7,8,9]. Moreover, some algorithms have been developed for individual tree crown segmentation from ALS data, whether alone [10,11,12,13] or combined with other data sources to solve the most common limitation of ALS systems, the low density of points acquired. As a result, multi-data source approaches have been developed, for example, combing ALS with photogrammetry [14,15,16,17]. The accuracy of the results depends on the type of forest, species distribution, conditions, and stand structure [18]. On a smaller scale, where more accurate and detailed information is required, data has to be collected at plot level or even at individual tree level. In this last case, traditional methods that use calipers and hypsometers are still normally used [19]. However, these methods are slow, prone to human error, and cannot reconstruct the geometry of the trees. In the last decade, the use of terrestrial laser scanning (TLS) for precise forest inventory has been analyzed [20,21,22,23,24,25,26,27,28,29]. 3D point cloud from TLS is dense enough to allow spatial location of the trees and to extract almost the whole geometry of each tree with high precision. Despite the advantages of TLS for precise forest inventory, the time spent on data collection, due to its static nature, and the point cloud processing that is required mean that this technology has not been introduced yet among forest technicians [30]. However, the emergence of the wearable laser scanner (WLS) with real-time registering can substantially reduce these drawbacks.

WLS combines laser scanning technology and inertial measurement units (IMU) in a portable equipment that can be handled by a single operator while walking during acquisition [31,32]. These systems are capable of digitalizing complex 3D scenarios on the move without a global navigation satellite system (GNSS), thanks to simultaneous localization and mapping (SLAM) algorithms [33,34], and are based mostly on ROS (Robotic Operative System) [35] for point cloud registration and map extraction. Regarding the quality of the data, these devices usually offer a centimeter-level accuracy [36] and a resolution that depends on the acquisition speed and the distance to the object in each moment. Although these devices are more suitable for indoor use due to their greater productivity and efficiency than for outdoor use [37], they have been used successfully for the reconstruction of outdoor scenarios such as cultural heritage, civil engineering, and urban inventory, among others [38,39]. Consequently, it is necessary to analyze in depth the possibilities offered by these systems for forest inventory, as well as their limitations, and evaluate their advantages and disadvantages as a possible step toward strengthening forest resource management.

In this work, we compare the results obtained using a TLS and a WLS system for tree detection and determine two essential dendrometric variables for forest inventory: diameter of the trunk at breast height (DBH) and the maximum height of the tree crown or tree total height (TH). We analyze the particularities of each system in obtaining the point cloud and we process automatically the raw point clouds in order to detect all the trees and obtain both variables. The tests have been performed on two plots in different environments.

2. Materials and Methods

2.1. Equipment

The material used to perform this comparative study included two data acquisition devices, a WLS and a TLS device, and a set of 10 reference spheres (targets) to provide an external reference frame for the accuracy assessment between WLS and TLS. In addition, these targets were used as reference points for the alignment between the individual TLS scans.

2.1.1. Wearable Laser Scanner

The WLS device used to perform the study was the ZEB-REVO lightweight mobile laser scanner (Figure 1) commercialized by GeoSLAM [40]. It integrates a rotating 2D scanning device (Hokuyo UTM-30LX-F; Hokuyo Automatic Co., Ltd. Osaka, Japan) and an IMU in the handle. The batteries and the data storage and processing units are located in a small backpack. The system acquires three-dimensional information of the area under study, thanks to the motion offered by the scanning head on the motor drive, enabling the application of 3D-SLAM algorithms. The data acquisition is performed within the default range of 0.60–30 m indoors and 0.60–15 m outdoors, with a measurement rate of 40,000 points per second. For optimal results, data acquisition must start and finish at the same position, using walking patterns that ensure maximum coverage of all trees. The relative accuracy of the measured points is 2–3 cm in normal lighting conditions [36]. This WLS device works at 905 nm wavelength but does not store the backscattered laser intensity data.

Table 1. Technical specifications of the GeoSLAM ZEB-REVO device.

Parameter	Value
Laser measuring principle	Time of flight
Operating time (h)	4
Total device dimensions (mm)	220 × 180 × 470
Scanner dimensions (mm)	86 × 113 × 287
Total device weight (kg)	4.10
Scanner weight (kg)	1.00
Scanner resolution	0.625° H × 1.8° V
Wavelength (nm)	905
Head rotation speed (Hz)	0.5
Orientation system	MEMS IMU
Camera	GoPro

shows further details and technical specifications of this equipment.

2.1.2. Terrestrial Laser Scanner

The forest reference model was obtained with a FARO Focus3D TLS device (Figure 2). This infrared laser scanner measures distances using the principle of phase shift in the range of 0.60–120 m at a wavelength of 905 nm. Its field of view covers 320° vertically and 360° horizontally with an angular resolution of 0.009°, and has a measurement rate of 976,000 points per second. Regarding the quality of the data, it has a precision of ±2 mm in normal lighting conditions and a beam divergence of 0.19 mrad.

2.2. Study Sites

The proposed methodology was tested in two pine forest environments, one located in an urban green area and another in a rural environment.

The first study site chosen was the San Antonio Park (test site A), an urban green space with about 6.5 ha of trees located in the northeastern part of Ávila (Spain). This urban public garden space is part of the ancient gardens and orchards of the Convent in San Antonio, from which it receives its current name. The gardens and orchards are still preserved and located in the northern corner of the park (Figure 3). Since it is an urban park located in a busy area of the city, the study area was set up in the less crowded part of the park, delimited by the orange polygon in Figure 3. This area contains a 1 ha fully stocked, mixed two-aged stand of Pinus pinea and Platanus hispanica.

The second study site (test site B) was located near El Espinar, a municipality located in the southwest of the province of Segovia (Spain). This pine forest is found in a typical mountain ecosystem where Pinus sylvestris is the predominant species. The area selected for data collection was a 0.5 ha fully stocked, even-aged, pure stand on a 20% slope area (Figure 4).

2.3. Methodology

In this study, the performance of a WLS device for tree detection and the estimation of basic dendrometric variables were evaluated. This evaluation was carried out by comparing the results obtained from TLS and WLS point clouds. Both point clouds were processed to detect the tree stems and estimate the DBH and TH using methodology based on the algorithm described in [28]. Figure 5 shows the main steps of the entire process (i.e., data acquisition and forest plot variables estimation).

2.3.1. Data Acquisition

Prior to data collection, a reference network was set up to register (i) the different scans from TLS, and (ii) the final point clouds from TLS and WLS in the same coordinate system. As shown in Figure 6, the reference network was made up of spheres mounted on tripods.

WLS data acquisition requires a preliminary inspection of the area of interest in order to (i) plan a suitable data acquisition path, (ii) detect possible obstacles (the trees themselves, artifacts, etc.) that would affect it, and, (iii) identify possible unfavorable scenarios for the 3D SLAM registration. With this last, we refer to environments that are usually lacking characteristic elements that help the estimation of the sensor trajectory and thus the successful performance of the SLAM algorithms, such as in corridors or tunnels where there are repetitive elements. In addition, the IMU integrated into the scanning head is capable of measuring angular velocities and linear accelerations that help to calculate the sensor trajectory.

As reported in the equipment specifications (Section 2.1), the ZEB-REVO has a maximum acquisition range of 15 m outdoors. However, on very sunny days, this range can diminish. This must be taken into account when planning the trajectories of the WLS. In addition, treetops above a certain height are not expected to be acquired (Figure 7), which is considered a hindrance for tree monitoring.

Data acquisition with ZEB-REVO needs to start with the IMU initialization to establish the coordinate reference system. Then, the measurements begin and the 3D data is stored in real time on the hard drive located in the backpack. The data collection ends at the point where the IMU is initialized. As recommended by the ZEB-REVO manufacturer, scans should not exceed 20 min in order to avoid drifts and misalignments in the processing step. Longer data collections should be split into different rings and subsequently registered.

The TLS data acquisition must be designed so that the entire area of interest can be covered with the minimum number of scanning stations. In this way, alignment errors in the final forest model can be reduced. In addition, the TLS must be configured with a resolution that would allow a precise determination of the forestry parameters to be evaluated [28,41].

2.3.2. Point Clouds Pre-Processing and Registration

Data captured by the ZEB-REVO WLS are automatically processed through the desktop GeoSLAM software. First, 3D models are created for each individual ring. Then, if more than one scan/ring is required, an alignment process between the different scanning rings is performed to obtain the final 3D model. In that case, a sufficient overlap between consecutive scans has to be guaranteed. If a network of reference targets is used, at least three common targets must be recorded between consecutive scans. Figure 8a shows the scanning rings used to cover the study area.

The individual TLS point cloud alignment is done by a solid-rigid transformation using the network of reference spheres, as shown in Figure 8b. The proposed workflow guarantees a high final precision (around 3 mm) of the coordinates of the center of the reference spheres.

2.3.3. Tree Detection and Estimation of DBH and TH

To detect the trees in a laser point cloud and obtain the desired dendrometric variables for each individual tree, particularly the DBH and the TH, we implemented an adapted version of the algorithm described in [42], valid for both TLS and WLS datasets. This algorithm was structured following a sequence of steps that is explained below:

(1) Terrain modeling

DBH and TH are calculated considering the ground as a reference surface; therefore, we first need to construct the digital elevation model (DEM) from the point cloud. To do so, a regular mesh covering each test site is created and the planar coordinates of the centroid and the lowest point in each cell are calculated. Often, the lowest points in each cell correspond to the points under the terrain (downward outliers); therefore, it is advisable not to select the lowest point but that which corresponds to a specific elevation percentile (e.g., the 1% elevation percentile) and remove those points below this lower threshold level. In addition, it may also happen that the lowest point in each cell is not located in the terrain but above it (i.e., when the lowest point in a cell corresponds to a branch). To avoid these points (upward outliers), the algorithm compares the height of the lowest point in each cell with that of its eight closest neighbors. If the difference is larger than a threshold that represents the maximum expected elevation gap between neighbors, the elevation of the cell is set to that of its lowest neighbor. Normally, the elevation gap between neighbors decreases with the iterations, but sometimes increases, and this can lead to a flat model at the elevation of the lowest point of the mesh. In these cases, the algorithm automatically increases the initial elevation threshold and continues with the iterations. The iteration procedure stops when there are no gaps larger than the threshold. Figure 9 shows a DEM example at the beginning and after removing downward and upward outliers.

Heights are normalized by subtracting the Z coordinate of each cell centroid from the rest of the points in that cell. The effect obtained is equivalent to transforming the ground into a horizontal plane, dragging the rest of the points in the point cloud. The resulting normalized DEM is used as a starting point in the following two steps.

(2) DBH estimation

To estimate the diameter at breast height from the point cloud, it is necessary to first detect the tree trunks. The procedure starts limiting the analysis to a horizontal strip between two heights Z_low − Z_high (e.g., 1 and 3 m above the terrain; Figure 10). Those values define a region where the trunks are expected to be found without being interconnected by the ground (or low vegetation) or by other trunks through leaves or branches. Then, the original point cloud restricted to the strip is voxelized to create a reversible and simplified version of the point cloud defined by a regular mesh of voxel centroids [43]. In that way, the computing complexity decreases. As Figure 10 shows, adjacent voxels are joined and those with vertical continuity through the whole strip are labeled as candidate trunks.

Once the section of each trunk within the strip has been determined, the points contained in a section around 1.3 m (±h) above the terrain are selected, h being a tolerance (i.e., 0.05 m) that ensures sufficient points to adjust a circle. The (X,Y) coordinates of those points are used for circle fitting by means of a nonlinear least squares algorithm [44,45]. Sometimes, the vertical section around 1.3 m contains points that do not belong to the trunk but rather are other parts such as branches or bushes. In this case, the circle fitting can give place to an erroneous estimation of the trunk radius R. To avoid this, we look for points in a concentric inner circle with radius R’ = R/2. If that kind of point exists, all the points in the vertical section are grouped based on the distance. Assuming that the cluster with the maximum number of points should correspond to the trunk and not to branches or bushes, a new circle is fitted to those points. If there are still points within the circle of radius R’ or if their values are anomalous, they are removed or labeled by visual inspection. Figure 11 shows the method proposed for circle fitting.

(3) TH estimation

To estimate the total tree height, the tree crowns are obtained first by selecting the points inside a vertical prism, which base is defined by the Voronoi polygons [46] of trunk centers obtained in the previous step (Figure 12a). Then, the highest point in each prism is identified, its normalized elevation being the TH (Figure 12b). As there may be outliers, a previous detection and removal of isolated high points that do not belong to the tree crown are performed. As in step 2, we worked with the voxelized point cloud to speed up the procedure.

3. Results

3.1. Data Acquisition and Point Cloud Registration

To perform the data acquisition at both study sites, the reference system was set up using expanded polystyrene spheres. Specifically, 10 spheres of 200 mm diameter were fixed to topographic tripods and distributed throughout the scene to guarantee their visibility. Measurements at both test sites took place in daylight and on sunny, clear days. These climate conditions decrease the laser range of the WLS device, as explained in Section 2.3.1.

At test site A (Figure 13), four scanning paths of 15 min duration were necessary to ensure a full coverage of the study area of 1 ha with the ZEB-REVO. TLS data acquisition with the FARO Focus3D was performed from 10 scan setups with a grid resolution of 6 mm at 10 m. The root mean square error (RMSE) of the registration was 34 mm for the WLS dataset and 3.4 mm for the TLS dataset. Finally, both forest models were decimated to 5 mm resolution in order to have a lighter product that facilitates the subsequent processes. A final 3D model of 54 million points for WLS data collection was obtained against the 70 million point cloud for the TLS data collection.

At test site B (Figure 14), only one scanning ring of 15 min with the ZEB-REVO was necessary to cover the selected area of study. In this case, TLS data acquisition with the FARO Focus3D was performed from four scan setups with a grid resolution of 3 mm at 10 m. The RMSE of the registration was 30 mm for the WLS dataset and 2.9 mm for the TLS dataset. Finally, both point clouds were decimated to 10 mm resolution, obtaining a 3D model of 9.5 million points for the WLS data collection and 77 million points for the TLS. Figure 14 shows the two final forest 3D models registered and superimposed.

3.2. DBH and TH Estimation

The algorithm for individual tree segmentation and dendrometric variables estimation was tested in the two scenarios (A and B) previously described, and the results obtained from both laser systems were compared. Figure 15 shows the probability density functions for DBH and TH at both test sites. Note that the variability of TH at site A was much larger than at site B.

The same number of trees was detected at both test sites after applying the algorithm to the TLS and WLS datasets: 195 trees at A and 76 at B. RMSE of the location differences between the trees detected from TLS and WLS point clouds was 3.5 cm at test site A and 2.4 cm at test site B. Figure 16 shows individualized trees in random colors from the WLS and TLS datasets.

Differences in DBH and TH estimations from both data sources were computed for the two test sites.

Table 2. RMSE, mean, standard deviation (m) of the differences in diameter at breast height (DBH) and tree height (TH) between terrestrial laser scanning (TLS) and wearable laser scanning (WLS) data at the two test sites.

	DBH		TH
Test Site	A	B	A	B
Mean	−0.001	−0.001	0.940	9.030
Standard deviation	0.011	0.009	0.960	2.760
RMSE	0.011	0.009	1.340	9.440

summarizes the RMSE, mean, and standard deviation of the differences. Figure 17 shows the correspondence between TLS and WLS point clouds for the DBH and TH estimations. The TH values were different for sites A and B.

The possible presence of bias in the DBH and TH differences between the results from the TLS and WLS datasets was tested using standardized average values from 10,000 bootstrap samples:

$$\Delta DB{H}_i^{*}=\frac{{\overline{\Delta DBH}}_i-\overline{\Delta DBH}}{\frac{{\sigma }_{{\overline{\Delta DBH}}_i}}{\sqrt{n}}}$$

(1)

where $\Delta DB{H}_i^{*}$ (i = 1, …, 1000) is the standardized mean of DBH differences in each bootstrap sample; ${\overline{\Delta DBH}}_i$ is the average value of each sample and $\overline{\Delta DBH}$ is the average value of the population; ${\sigma }_{{\overline{\Delta DBH}}_i}$ is the standard deviation of each sample; and n is the total number of detected trees (i.e., 271). Values for $\Delta T{H}_i^{*}$ were similarly calculated.

Considering the null hypothesis H0: the average difference is 0, where p-values for DBH and TH differences were 0.513 and 0, respectively. Therefore, H0 is rejected for TH at a significance level of 1%, and H0 cannot be rejected for DBH at a significance level of 5%. Alternatively, as shown in Figure 18 and

Table 3. RMSE, mean, and standard deviation (m) of the differences in TH between TLS and WLS data and p-values (H0: average TH differences are 0) for all the trees at test sites A and B, as well as for three data subsets: trees with TH estimated from the TLS dataset smaller than 10, 9, and 8 m.

	All Trees	TH <10 m	TH <9 m	TH <8 m
Number of trees	271	79	68	52
p-value	0.000	0.012	0.112	0.517
RMSE	3.790	0.740	0.730	0.650
Mean	2.790	0.210	0.140	−0.060
Standard deviation	2.950	0.710	0.720	0.660

, a similar analysis was carried out on the TH differences of three data subsets: trees with THs smaller than 10, 9, and 8 m (i.e., subsets were based on the TH estimation from the TLS datasets).

The p-values shown in Table 3 indicate that H0 cannot be rejected for TH at a significance level of 1% for trees smaller than 10 m. In the same way, H0 cannot be rejected for TH at a significance level of 5% for trees smaller than 9 m.

4. Discussion

The same number of trees was detected at both test sites using the WLS and TLS datasets. Thus, in the test plots used in this study, we did not find any difference in individual tree detection using the two scanning systems. Moreover, there is no apparent reason why differences in tree detection could arise, as long as both point clouds adequately cover the plot area, at least within the vertical strip (see Section 2.3.3).

The diameter at breast height (DBH) and tree height (TH) estimations were evaluated by comparing the results from WLS and TLS point clouds. This comparison was carried out in two different ways: (i) assessing separately the differences between both methods at each test site (Figure 16 and Figure 17 and Table 2), and (ii) through the evaluation of the possible presence of bias in the DBH and TH estimation in the whole population of detected trees (Figure 18 and Table 3).

As shown in Table 2 and Figure 17, DBH differences were similar at both test sites despite the tree species (i.e., Pinus sylvestris and Platanus hispanica at test site A and Pinus pinea at test site B) and the uneven distribution of diameters at both test sites (Figure 16). Statistical tests carried out on the entire population of DBH differences suggest that the diameter estimations from WLS data were not biased at a significance level of 5% (Figure 18). The relative precision of the points gathered with WLS and PLS systems was clearly different (Section 2.1.1 and Section 2.1.2) and, as shown in Figure 13, the dispersion was clearly higher in points from WLS on the breast height sections. However, this fact did not affect the DBH estimation.

The use of ground-based laser scanning systems (e.g., TLS or WLS) often leads to underestimation of the total tree height [28]. In the case of TLS, this is mainly due to occlusions that do not allow enough points to be measured on the treetops. However, some WLS systems, such as the ZEB-REVO used in this study, add another limitation when used outdoors: the measurement range is very reduced and dependent on the illumination conditions. In this way, treetops above 15 m were not expected to be measured with this specific device and in unfavorable conditions (sunny days) this limit is expected to be reduced.

As shown in Figure 15 and Figure 16, TH distribution was very different at both study areas: Test site A contained two large groups of trees with heights around 9 and 15 m (i.e., Pinus sylvestris and Platanus hispanica, respectively), whereas the trees at test site B had similar heights of around 25 m. This TH distribution joined to the measurement conditions (i.e., sunny days) led to the results shown in Table 2 and Figure 17, and are summarized hereunder:

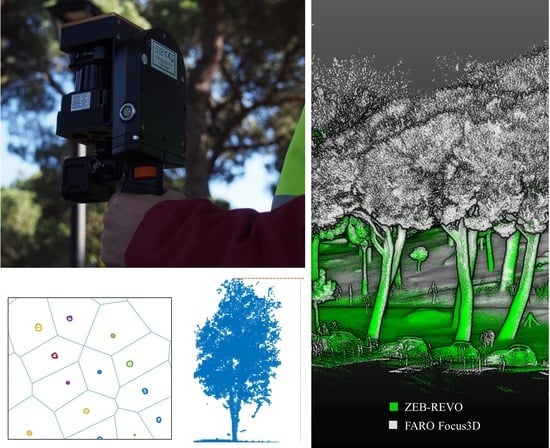
• TH differences were clearly higher at test site B where treetops were out of reach of the WLS. This is noticeable in Figure 16 where treetops were not represented in the WLS point cloud and in Figure 17 where the blue dots corresponding to the TH from test site B were clearly lower in the WLS estimation. RMSE and mean differences shown in Table 2 were substantially higher at test site B (around 9 m) than at test site A (around 1 m).
• At test site A, some of the trees were apparently on the limit or above the measurement range of the WLS (i.e., taller trees in Figure 16, corresponding to Pinus sylvestris). Figure 17 shows two groups in the TH comparison at test site A (i.e., the two different species in the plot). These two groups were clearly closer to the no-difference black line in the figure than the trees from test site B. However, differences between the two groups can be recognized in the graphic: underestimation from the WLS data is more evident in the group with taller TH.

Statistical tests computing all the trees show that there was a clear bias in TH estimation from WLS data with respect to TLS. Nevertheless, as shown in Table 3 and Figure 18, if these tests are carried out on data subsets of smaller trees (i.e., trees smaller than 10, 9, and 8 m, Table 3 and Figure 18), the results suggest that there would be no bias in TH estimation. In addition, Table 3 shows that RMSE, mean, and standard deviation of the differences in TH were substantially lower for smaller trees.

Summarizing, TH estimation comparison and statistical tests reveal the influence of the measurement range limit of the WLS device used in this study, as well as light and atmospheric conditions. This seems to be the only restrictive factor when comparing TH estimation from WLS and TLS: there was no apparent bias in TH estimations for trees smaller than a certain height. The height threshold, above which TH estimations fail, is dependent on the maximum measurement range of the WLS device and is subject to the illumination conditions.

Finally, it is worth highlighting the advantage of using WLS over TLS devices in terms of acquisition and processing time. For complex scenarios, as those presented in the paper, and large areas, WLS technology allows a final 3D model to be achieved in half the time needed than when using TLS technology. For simpler or smaller areas where a single WLS path is required, data acquisition time is reduced to a quarter of that required by TLS technology.

Table 4. Times required for the different operations to detect trees from point clouds and to estimate DBH and TH. Both measurement systems (TLS and WLS) and test sites are compared.

	Scanning		Pre-Processing		Post-Processing
	Test Site A	Test Site B	Test Site A	Test Site B	Test Site A	Test Site B
TLS	120 min	35 min	70 min	30 min	239 s	217 s
WLS	60 min	15 min	30 min	0 min	184 s	163 s

shows the times for scanning, pre-processing, and post-processing for both TLS and WLS systems.

5. Conclusions

In this paper, a wearable laser scanning (WLS) device has been presented and tested for forest mapping and inventory through the comparison of results obtained from a terrestrial laser scanning (TLS) device. The validation was carried out by assessing the performance in tree detection and the estimation of specific dendrometric variables: diameter at breast height (DBH) and total tree height (TH). In this way, both mapping and forest inventory capabilities have been evaluated.

Despite the lower relative precision of the points recorded with the WLS device, results show that the performance of WLS for tree detection and DBH estimation is equivalent to that from TLS: there is no apparent difference in tree detection nor significant bias in DBH estimation. Nevertheless, TH results show a clear underestimation with respect to TLS when trees surpass a certain height. This fact is due to the measurement range limit of the WLS device used in this study (ZEB-REVO), a maximum scanning range of 15 m, and lower depending on illumination conditions.

There is no apparent difference nor bias in tree detection using WLS and TLS in trees smaller than 9 or 10 m. This suggests that TH estimations from WLS data are equivalent to those from TLS unless the trees are taller than the scanning range, determined by the WLS device characteristics and the measurement conditions.

Given the nature of the algorithm used for tree detection and DBH estimation and the aforementioned limitations in TH estimations, further studies on the use of WLS for automatic dendrometry in forest plots could focus on the assessment of stem-profile functions for wood volume estimation.