A Comparison between Standard and Functional Clustering Methodologies: Application to Agricultural Fields for Yield Pattern Assessment
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Landsat Dataset
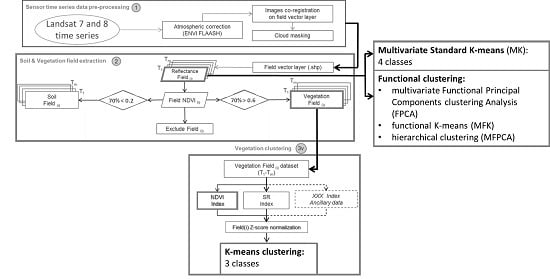
2.2. Landsat Time Series Processing Chain and Standard K-Means Clustering
2.3. Clustering Methods for Multilevel Functional Data
2.3.1. Silhouette Index
2.3.2. Multivariate K-Means (MK)
2.3.3. Functional K-Means (MFK)
2.3.4. Multivariate Functional Clustering (FPCA)
2.3.5. Hierarchical Clustering (MFPCA)
2.4. Clustering Accuracy Assessment
3. Results
3.1. Clustering Results
3.1.1. Standard K-Means Clustering Results
3.1.2. Functional Clustering Results
3.2. Ability of Clustering Methods to Capture Actual Yield Patterns
4. Discussion
5. Conclusions
Acknowledgments
Author Contributions
Conflicts of Interest
References
- Blasch, G.; Spengler, D.; Hohmann, C.; Neumann, C.; Itzerott, S.; Kaufmann, H. Multitemporal soil pattern analysis with multispectral remote sensing data at the field-scale. Comput. Electron. Agric. 2015, 113, 1–13. [Google Scholar] [CrossRef]
- Huang, C.; Goward, S.N.; Masek, J.G.; Thomas, N.; Zhu, Z.; Vogelmann, J.E. An automated approach for reconstructing recent forest disturbance history using dense landsat time series stacks. Remote Sens. Environ. 2010, 114, 183–198. [Google Scholar] [CrossRef]
- Verbesselt, J.; Hyndman, R.; Newnham, G.; Culvenor, D. Detecting trend and seasonal changes in satellite image time series. Remote Sens. Environ. 2010, 114, 106–115. [Google Scholar] [CrossRef]
- FARMSTAR. Available online: http://www.farmstar-conseil.fr/ (accessed on 5 August 2017).
- ERMES (an Earth obseRvation Model Based ricE Information Service). Available online: http://www.ermes-fp7space.eu/en/about-ermes/ (accessed on 1 October 2017).
- Ge, Y.; Thomasson, J.A.; Sui, R. Remote sensing of soil properties in precision agriculture: A review. Front. Earth Sci. 2011, 5, 229–238. [Google Scholar] [CrossRef]
- Blasch, G.; Spengler, D.; Itzerott, S.; Wessolek, G. Organic matter modeling at the landscape scale based on multitemporal soil pattern analysis using RapidEye data. Remote Sens. 2015, 7, 11125–11150. [Google Scholar] [CrossRef]
- Mulla, D.J. Twenty five years of remote sensing in precision agriculture: Key advances and remaining knowledge gaps. Biosyst. Eng. 2013, 114, 358–371. [Google Scholar] [CrossRef]
- Eerens, H.; Haesen, D.; Rembold, F.; Urbano, F.; Tote, C.; Bydekerke, L. Image time series processing for agriculture monitoring. Environ. Model. Softw. 2014, 53, 154–162. [Google Scholar] [CrossRef]
- Bellón, B.; Bégué, A.; Lo Seen, D.; de Almeida, C.A.; Simões, M. A remote sensing approach for regional-scale mapping of agricultural land-use systems based on NDVI time series. Remote Sens. 2017, 9, 600. [Google Scholar] [CrossRef]
- Baruth, B.; Royer, A.; Klisch, A.; Genovese, A. The Use of Remote Sensing within the MARS Crop Yield Monitoring System of the European Commission; ISPRS, Commission VIII: Stresa, Italy, 2008; pp. 935–941. [Google Scholar]
- Becker-Reshef, I.; Justice, C.; Sullivan, M.; Vermote, E.; Tucker, C.; Anyamba, A.; Small, J.; Pak, E.; Masuoka, E.; Schmaltz, J.; et al. Monitoring global croplands with coarse resolution earth observations: The Global Agriculture Monitoring (GLAM) Project. Remote Sens. 2010, 2, 1589–1609. [Google Scholar] [CrossRef]
- Casa, R.; Castrignanò, A. Analysis of spatial relationships between soil and crop variables in a durum wheat field using a multivariate geostatistical approach. Eur. J. Agron. 2008, 28, 331–342. [Google Scholar] [CrossRef] [Green Version]
- Castrignanò, A.; Buttafuoco, G.; Quarto, R.; Vitti, C.; Langella, G.; Terribile, F.; Venezia, A. A combined approach of sensor data fusion and multivariate geostatistics for delineation of homogeneous zones in an agricultural field. Sensors 2017, 17, 2794. [Google Scholar] [CrossRef] [PubMed]
- Tibshirani, R.; Walther, G.; Hastie, T. Estimating the number of clusters in a data set via the gap statistic. J. Roy. Statist. Soc. B 2001, 63, 411–423. Available online: http://www.web.stanford.edu/~hastie/Papers/gap.pdf (accessed on 18 October 2016). [CrossRef]
- Rousseeuw, P.J. Silhouettes: A graphical aid to the interpretation and validation of cluster analysis. J. Comput. Appl. Math. 1987, 20, 53–65. [Google Scholar] [CrossRef]
- Arbelaitz, O.; Gurrutxaga, I.; Muguerza, J.; Pérez, J.M.; Perona, I. An extensive comparative study of cluster validity indexes. Pattern Recognit. 2013, 46, 243–256. [Google Scholar] [CrossRef]
- Lozano, J.A.; Pena, J.M.; Larranaga, P. An empirical comparison of four initialization methods for the K-means algorithm. Pattern Recognit. Lett. 1999, 20, 1027–1040. [Google Scholar] [CrossRef]
- Zaady, E.; Karnieli, A.; Shachak, M. Applying a field spectroscopy technique for assessing successional trends of biological soil crusts in a semi-arid environment. J. Arid Environ. 2007, 70, 463–477. [Google Scholar] [CrossRef]
- Jain, A.K.; Flynn, P.J. Image segmentation using clustering. In Advances in Image Understanding; Wiley-IEEE Computer Society Press: Washington, DC, USA, 1996; pp. 65–83. [Google Scholar] [CrossRef]
- Jain, A.K. Data clustering: 50 years beyond K-means. Pattern Recognit. Lett. 2010, 31, 651–666. [Google Scholar] [CrossRef]
- Richards, J.W.; Hardin, J.; Grosfils, E.B. Weighted model-based clustering for remote sensing image analysis. Comput. Geosci. 2010, 14, 125–136. [Google Scholar] [CrossRef]
- Ma, A.; Zhong, Y.; Zhang, L. Spectral-Spatial Clustering with a Local Weight Parameter Determination Method for Remote Sensing Imagery. Remote Sens. 2016, 8, 124. [Google Scholar] [CrossRef]
- Choubin, B.; Solaimani, K.; Habibnejad Roshan, M.; Malekian, A. Watershed classification by remote sensing indexes: A fuzzy c-means clustering approach. J. Mt. Sci. 2017, 14, 2053. [Google Scholar] [CrossRef]
- Ng, A.; Jordan, M.; Weiss, Y. On spectral clustering: Analysis and an algorithm. In Advances in Neural Information Processing Systems; Dietterich, T., Becker, S., Ghahramani, Z., Eds.; MIT Press: Cambridge, UK, 2002; Volume 14, pp. 849–856. [Google Scholar]
- Von Luxburg, U. A tutorial on spectral clustering. Stat. Comput. 2007, 17, 395–416. [Google Scholar] [CrossRef]
- Rodriguez, A.; Laio, A. Clustering by fast search and find of density peaks. Science 2014, 344, 1492–1496. [Google Scholar] [CrossRef] [PubMed]
- Elhamifar, E.; Vidal, R. Sparse manifold clustering and embedding. Adv. Neural Inf. Process. Syst. 2011, 24, 55–63. [Google Scholar]
- Murphy, J.M.; Maggioni, M. Nonlinear Unsupervised Clustering of Hyperspectral Images with Applications to Anomaly Detection and Active Learning, Computer Science—Computer Vision and Pattern Recognition. arXiv, 2017; arXiv:1704.07961. [Google Scholar]
- Little, A.; Maggioni, M.; Murphy, J.M. Path-Based Spectral Clustering: Guarantees, Robustness to Outliers, and Fast Algorithms. arXiv, 2017; arXiv:1712.06206. [Google Scholar]
- Little, A.; Byrd, A. A Multiscale Spectral Method for Learning Number of Clusters. In Proceedings of the 2015 IEEE 14th International Conference on Machine Learning and Applications (ICMLA), Miami, FL, USA, 9–11 December 2015. [Google Scholar]
- Jebara, T.; Song, Y.; Thadani, K. Spectral Clustering and Embedding with Hidden Markov Models. In Machine Learning: ECML 2007. ECML 2007. Lecture Notes in Computer Science; Kok, J.N., Koronacki, J., Mantaras, R.L., Matwin, S., Mladenič, D., Skowron, A., Eds.; Springer: Berlin/Heidelberg, Germany, 2017; Volume 4701. [Google Scholar]
- Jacques, J.; Preda, C. Functional data clustering: A survey. Adv. Data Anal. Classif. 2014, 8, 231–255. [Google Scholar] [CrossRef]
- Ieva, F.; Paganoni, A.M.; Pigoli, D.; Vitelli, V. Multivariate functional clustering for the morphological analysis of electrocardiograph curves. J. R. Stat. Soc. Ser. C 2013, 62, 401–418. [Google Scholar] [CrossRef]
- Serban, N.; Jiang, H. Multilevel Functional Clustering Analysis. Biometrics 2012, 68, 805–814. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Deng, X.; Dolloff, C.A.; Smith, E.P. Bivariate functional data clustering: Grouping streams based on a varying coefficient model of the stream water and air temperature relationship. Environmetrics 2015, 27, 15–26. [Google Scholar] [CrossRef]
- Romano, E.; Mateu, J.; Giraldo, R. On the performance of two clustering methods for spatial functional data. Adv. Stat. Anal. 2015, 99, 467–492. [Google Scholar] [CrossRef]
- Gaetan, C.; Girardi, P.; Pastres, R. Spatial clustering of curves with an application of satellite data. Spat. Stat. 2017, 20, 110–124. [Google Scholar]
- Haggarty, R.; Miller, C.M.; Scott, E.; Wyllie, F.; Smith, M. Functional clustering of water quality data in Scotland. Environmetrics 2012, 23, 685–695. [Google Scholar] [CrossRef]
- Luz-López-García, M.; García-Ródenas, R.; González-Gómez, A. K-means algorithms for functional data. Neurocomputing 2015, 151, 231–245. [Google Scholar] [CrossRef]
- Berrendero, J.R.; Justel, A.; Svarc, M. Principal components for multivariate functional data. Comput. Stat. Data Anal. 2011, 55, 2619–2634. [Google Scholar] [CrossRef]
- Di, C.Z.; Crainiceanu, C.M.; Caffo, B.S.; Punjabi, N.M. Multilevel functional principal component analysis. Ann. Appl. Stat. 2009, 3, 458–488. [Google Scholar] [CrossRef] [PubMed]
- Nguyen, C.; Starek, M.J.; Tissot, P.; Gibeaut, J. Unsupervised Clustering Method for Complexity Reduction of Terrestrial Lidar Data in Marshes. Remote Sens. 2018, 10, 133. [Google Scholar] [CrossRef]
- Tu, W.; Hu, Z.; Li, L.; Cao, J.; Jiang, J.; Li, Q.; Li, Q. Portraying Urban Functional Zones by Coupling Remote Sensing Imagery and Human Sensing Data. Remote Sens. 2018, 10, 141. [Google Scholar] [CrossRef]
- Goovaerts, P. Kriging and semivariogram deconvolution in the presence of irregular geographical units. Math. Geosci. 2008, 40, 101–128. [Google Scholar] [CrossRef]
- FAO-ISRIC-ISSS. World Reference Base for Soil Resources; World Soil Resources Report 84; Food and Agriculture Organization: Rome, Italy, 1998. [Google Scholar]
- ENVI/IDL Scientific Programming Language. Available online: http://www.envi geospatial.com/ProductsandSolutions/GeospatialProducts/IDL.aspx (accessed on 10 October 2016).
- Matthew, M.W.; Adler-Golden, S.M.; Berk, A.; Richtsmeier, S.C.; Levine, R.Y.; Bernstein, L.S.; Acharya, P.K.; Anderson, G.P.; Felde, G.W.; Hoke, M.P.; et al. Status of Atmospheric Correction Using a MODTRAN4-based Algorithm. In SPIE Proceedings, Algorithms for Multispectral, Hyperspectral, and Ultraspectral Imagery VI; AeroSense 2000: Orlando, FL, USA, 2000; Volume 4049, pp. 199–207. [Google Scholar]
- Yengoh, G.T.; Dent, D.; Olsson, L.; Tengberg, A.E.; Tucker, C.J., III. Use of the Normalized Difference Vegetation Index (NDVI) to Assess Land Degradation at Multiple Scales; Springer Briefs in Environmental Science; Springer International Publishing: Berlin, Germany, 2016; pp. 1–110. [Google Scholar]
- Reichenau, T.G.; Korres, W.; Montzka, C.; Fiener, P.; Wilken, F.; Stadler, A.; Waldhoff, G.; Schneider, K. Spatial Heterogeneity of Leaf Area Index (LAI) and Its Temporal Course on Arable Land: Combining Field Measurements, Remote Sensing and Simulation in a Comprehensive Data Analysis Approach (CDAA). PLoS ONE 2016, 11, e0158451. [Google Scholar] [CrossRef] [PubMed]
- Zhu, Z.; Woodcock, C.E.; Olofsson, P. Continuous monitoring of forest disturbance using all available Landsat imagery. Remote Sens. Environ. 2012, 122, 75–91. [Google Scholar] [CrossRef]
- De Amorim, R.C.; Hennig, C. Recovering the number of clusters in data sets with noise features using feature rescaling factors. Inf. Sci. 2015, 324, 126–145. [Google Scholar] [CrossRef] [Green Version]
- R. Package Fda. Available online: https://cran.r-project.org/web/packages/fda/fda.pdf (accessed on 10 October 2017).
- Castaldi, F.; Casa, R.; Pelosi, F.; Yang, H. Influence of acquisition time and resolution on wheat yield estimation at the field scale from canopy biophysical variables retrieved from SPOT satellite data. Int. J. Remote Sens. 2015, 36, 2438–2459. [Google Scholar] [CrossRef]
- Wiwie, C.; Baumbach, J.; Röttger, R. Comparing the performance of biomedical clustering methods. Nat. Methods 2015, 12, 1033–1038. [Google Scholar] [CrossRef] [PubMed]
- Buttafuoco, G.; Castrignanò, A.; Cucci, G.; Lacolla, G.; Lucà, F. Geostatistical modelling of within-field soil and yield variability for management zones delineation: A case study in a durum wheat field. Precis. Agric. 2017, 18, 37–58. [Google Scholar] [CrossRef]
- Buttafuoco, G.; Castrignanò, A.; Cucci, G.; Rinaldi, M.; Ruggieri, S. An approach to delineate management zones in a durum wheat field: Validation using remote sensing and yield mapping. In Precision Agriculture ’15; Wageningen Academic Publishers: Wageningen, The Netherlands, 2015; pp. 241–248. [Google Scholar]
- Diacono, M.; Castrignanò, A.; Vitti, C.; Stellacci, A.M.; Marino, L.; Cocozza, C.; De Benedetto, D.; Troccoli, A.; Rubino, P.; Ventrella, D. An approach for assessing the effects of site-specific fertilization on crop growth and yield of durum wheat in organic agriculture. Precis. Agric. 2014, 15, 479–498. [Google Scholar] [CrossRef]
- Casa, R.; Castaldi, F.; Pascucci, S.; Basso, B.; Pignatti, S. Geophysical and hyperspectral data fusion techniques for in-field estimation of soil properties. Vadose Zone J. 2013, 12. [Google Scholar] [CrossRef]
- Castaldi, F.; Palombo, A.; Santini, F.; Pascucci, S.; Pignatti, S.; Casa, R. Evaluation of the potential of the current and forthcoming multispectral and hyperspectral imagers to estimate soil texture and organic carbon. Remote Sens. Environ. 2016, 179, 54–65. [Google Scholar] [CrossRef]






| FOI | Area (ha) | Year | K-Means | MK | MFK | FPCA | MFPCA | OPT | |||||
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| E | S | E | S | E | S | E | S | E | S | ||||
| 10 | 9.0 | 2007 | 3 | 2 | 5 | 4 | 4 | 4 | 4 | 3 | 4 | 4 | 4 |
| 10 | 9.0 | 2010 | 3 | 3 | 5 | 4 | 4 | 3 | 4 | 4 | 4 | 4 | 4 |
| 13 | 15.6 | 2007 | 3 | 3 | 2 | 2 | 2 | 2 | 2 | 2 | 4 | 4 | 3 |
| 13 | 15.6 | 2010 | 3 | 3 | 2 | 2 | 2 | 2 | 2 | 2 | 4 | 4 | 3 |
| 24 | 15.6 | 2010 | 3 | 3 | 5 | 5 | 6 | 6 | 3 | 3 | 4 | 3 | 6 |
| 24 | 15.6 | 2016 | 3 | 3 | 5 | 4 | 6 | 5 | 3 | 3 | 4 | 4 | 6 |
| 25 | 2.8 | 2009 | 3 | 2 | 2 | 2 | 3 | 2 | 3 | 3 | 4 | 2 | 3 |
| 30 | 7.8 | 2010 | 3 | 3 | 2 | 2 | 2 | 2 | 2 | 2 | 4 | 3 | 3 |
| 36 | 9.6 | 2009 | 3 | 3 | 5 | 4 | 5 | 4 | 5 | 4 | 4 | 4 | 4 |
| 39 | 16.9 | 2009 | 3 | 3 | 4 | 3 | 8 | 7 | 7 | 6 | 4 | 4 | 7 |
| 54 | 20.1 | 2009 | 3 | 2 | 2 | 2 | 2 | 2 | 2 | 2 | 4 | 4 | 2 |
| 54 | 20.1 | 2010 | 3 | 3 | 2 | 2 | 2 | 2 | 2 | 2 | 4 | 4 | 3 |
| 27 | 15.3 | 2016 | 3 | 3 | 4 | 4 | 4 | 4 | 2 | 2 | 4 | 4 | 4 |
| 64 | 55.6 | 2017 | 3 | 3 | 8 | 8 | 5 | 5 | 2 | 2 | 4 | 3 | 8 |
| 77 | 41.1 | 2017 | 3 | 3 | 5 | 5 | 6 | 5 | 2 | 2 | 4 | 4 | 5 |
| 78 | 52.6 | 2017 | 3 | 3 | 2 | 2 | 2 | 2 | 2 | 2 | 4 | 4 | 4 |
| 83 | 45.4 | 2017 | 3 | 3 | 3 | 3 | 2 | 2 | 2 | 2 | 4 | 4 | 4 |
| 94 | 32.8 | 2017 | 3 | 3 | 5 | 4 | 3 | 3 | 3 | 3 | 4 | 4 | 4 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Pascucci, S.; Carfora, M.F.; Palombo, A.; Pignatti, S.; Casa, R.; Pepe, M.; Castaldi, F. A Comparison between Standard and Functional Clustering Methodologies: Application to Agricultural Fields for Yield Pattern Assessment. Remote Sens. 2018, 10, 585. https://doi.org/10.3390/rs10040585
Pascucci S, Carfora MF, Palombo A, Pignatti S, Casa R, Pepe M, Castaldi F. A Comparison between Standard and Functional Clustering Methodologies: Application to Agricultural Fields for Yield Pattern Assessment. Remote Sensing. 2018; 10(4):585. https://doi.org/10.3390/rs10040585
Chicago/Turabian StylePascucci, Simone, Maria Francesca Carfora, Angelo Palombo, Stefano Pignatti, Raffaele Casa, Monica Pepe, and Fabio Castaldi. 2018. "A Comparison between Standard and Functional Clustering Methodologies: Application to Agricultural Fields for Yield Pattern Assessment" Remote Sensing 10, no. 4: 585. https://doi.org/10.3390/rs10040585
APA StylePascucci, S., Carfora, M. F., Palombo, A., Pignatti, S., Casa, R., Pepe, M., & Castaldi, F. (2018). A Comparison between Standard and Functional Clustering Methodologies: Application to Agricultural Fields for Yield Pattern Assessment. Remote Sensing, 10(4), 585. https://doi.org/10.3390/rs10040585