A Cloud-Based Multi-Temporal Ensemble Classifier to Map Smallholder Farming Systems
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area and Data
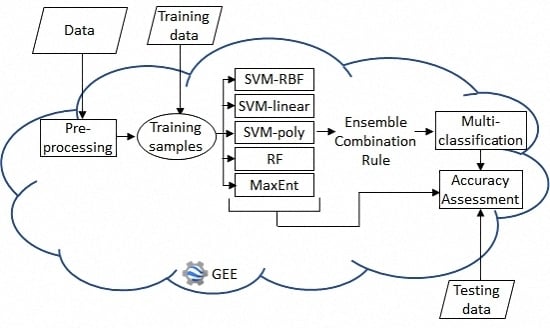
2.2. Methods
2.2.1. Data Preparation
2.2.2. Base Classifiers
2.2.3. Ensemble Classifiers
3. Experiment Results and Discussion
3.1. Data Preparation
3.2. Base Classifiers and Ensembles
4. Conclusions and Future Work
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A. Textural Features Formulas
| Name/Formula | Name/Formula |
|---|---|
| Angular Second Moment | Contrast |
| Correlation | Variance |
| Inverse Difference Moment | Sum Average |
| Sum Variance | Sum Entropy |
| Entropy | Difference Variance variance of |
| Difference Entropy | Information Measures of Correlation 1 where, and are entropies of and |
| Information Measures of Correlation 2 , where | Maximal Correlation Coefficient where |
| Dissimilarity |
| Description | Formula |
|---|---|
| Inertia | |
| Cluster shade | |
| Cluster prominence |
References
- Lowder, S.K.; Skoet, J.; Singh, S. What do We Really Know about the Number and Distribution of Farms and Family Farms in the World? FAO: Rome, Italy, 2014. [Google Scholar]
- African Development Bank, Organisation for Economic Co-operation and Development, United Nations Development Programme. African Economic Outlook 2014: Global Value Chains and Africa’s Industrialisation; OECD Publishing: Paris, France, 2014. [Google Scholar]
- STARS-Project. About Us—STARS Project, 2016. Available online: http://www.stars-project.org/en/about-us/ (accessed on 1 June 2016).
- Haub, C.; Kaneda, T. World Population Data Sheet, 2013. Available online: http://auth.prb.org/Publications/Datasheets/2013/2013-world-population-data-sheet.aspx (accessed on 6 March 2017).
- Atzberger, C. Advances in Remote Sensing of Agriculture: Context Description, Existing Operational Monitoring Systems and Major Information Needs. Remote Sens. 2013, 5, 949–981. [Google Scholar] [CrossRef]
- Wu, B.; Meng, J.; Li, Q.; Yan, N.; Du, X.; Zhang, M. Remote sensing-based global crop monitoring: Experiences with China’s CropWatch system. Int. J. Digit. Earth 2014, 113–137. [Google Scholar] [CrossRef]
- Khan, M.R. Crops from Space: Improved Earth Observation Capacity to Map Crop Areas and to Quantify Production; University of Twente: Enschede, The Netherlands, 2011. [Google Scholar]
- Debats, S.R.; Luo, D.; Estes, L.D.; Fuchs, T.J.; Caylor, K.K. A generalized computer vision approach to mapping crop fields in heterogeneous agricultural landscapes. Remote Sens. Environ. 2016, 179, 210–221. [Google Scholar] [CrossRef]
- Waldner, F.; Canto, G.S.; Defourny, P. Automated annual cropland mapping using knowledge-based temporal features. ISPRS J. Photogramm. Remote Sens. 2015, 110, 1–13. [Google Scholar] [CrossRef]
- Foody, G.M.; Mathur, A. Toward intelligent training of supervised image classifications: Directing training data acquisition for SVM classification. Remote Sens. Environ. 2004, 93, 107–117. [Google Scholar] [CrossRef]
- Beyer, F.; Jarmer, T.; Siegmann, B.; Fischer, P. Improved crop classification using multitemporal RapidEye data. In Proceedings of the 2015 8th International Workshop on the Analysis of Multitemporal Remote Sensing Images (Multi-Temp), Annecy, France, 22–24 July 2015; pp. 1–4. [Google Scholar]
- Camps-Valls, G.; Gomez-Chova, L.; Calpe-Maravilla, J.; Martin-Guerrero, J.D.; Soria-Olivas, E.; Alonso-Chorda, L.; Moreno, J. Robust support vector method for hyperspectral data classification and knowledge discovery. IEEE Trans. Geosci. Remote Sens. 2004, 42, 1530–1542. [Google Scholar] [CrossRef]
- Tatsumi, K.; Yamashiki, Y.; Torres, M.A.C.; Taipe, C.L.R. Crop classification of upland fields using Random forest of time-series Landsat 7 ETM+ data. Comput. Electron. Agric. 2015, 115, 171–179. [Google Scholar] [CrossRef]
- Yang, C.; Everitt, J.H.; Murden, D. Evaluating high resolution SPOT 5 satellite imagery for crop identification. Comput. Electron. Agric. 2011, 75, 347–354. [Google Scholar] [CrossRef]
- Sweeney, S.; Ruseva, T.; Estes, L.; Evans, T. Mapping Cropland in Smallholder-Dominated Savannas: Integrating Remote Sensing Techniques and Probabilistic Modeling. Remote Sens. 2015, 7, 15295–15317. [Google Scholar] [CrossRef]
- Lu, D.; Weng, Q. A survey of image classification methods and techniques for improving classification performance. Int. J. Remote Sens. 2007, 28, 823–870. [Google Scholar] [CrossRef]
- Waldner, F.; Li, W.; Weiss, M.; Demarez, V.; Morin, D.; Marais-Sicre, C.; Hagolle, O.; Baret, F.; Defourny, P. Land Cover and Crop Type Classification along the Season Based on Biophysical Variables Retrieved from Multi-Sensor High-Resolution Time Series. Remote Sens. 2015, 7, 10400–10424. [Google Scholar] [CrossRef]
- Jackson, R.D.; Huete, A.R. Interpreting vegetation indices. Prev. Vet. Med. 1991, 11, 185–200. [Google Scholar] [CrossRef]
- Peña-Barragán, J.M.; Ngugi, M.K.; Plant, R.E.; Six, J. Object-based crop identification using multiple vegetation indices, textural features and crop phenology. Remote Sens. Environ. 2011, 115, 1301–1316. [Google Scholar] [CrossRef]
- Rao, P.V.N.; Sai, M.V.R.S.; Sreenivas, K.; Rao, M.V.K.; Rao, B.R.M.; Dwivedi, R.S.; Venkataratnam, L. Textural analysis of IRS-1D panchromatic data for land cover classification Textural analysis of IRS-1D panchromatic data for land cover classication. Int. J. Remote Sens. 2002, 2317, 3327–3345. [Google Scholar] [CrossRef]
- Shaban, M.A.; Dikshit, O. Improvement of classification in urban areas by the use of textural features: The case study of Lucknow city, Uttar Pradesh. Int. J. Remote Sens. 2001, 22, 565–593. [Google Scholar] [CrossRef]
- Chellasamy, M.; Zielinski, R.T.; Greve, M.H. A Multievidence Approach for Crop Discrimination Using Multitemporal WorldView-2 Imagery. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2014, 7, 3491–3501. [Google Scholar] [CrossRef]
- Hu, Q.; Wu, W.; Song, Q.; Lu, M.; Chen, D.; Yu, Q.; Tang, H. How do temporal and spectral features matter in crop classification in Heilongjiang Province, China? J. Integr. Agric. 2017, 16, 324–336. [Google Scholar] [CrossRef]
- Misra, G.; Kumar, A.; Patel, N.R.; Zurita-Milla, R. Mapping a Specific Crop-A Temporal Approach for Sugarcane Ratoon. J. Indian Soc. Remote Sens. 2014, 42, 325–334. [Google Scholar] [CrossRef]
- Khobragade, N.A.; Raghuwanshi, M.M. Contextual Soft Classification Approaches for Crops Identification Using Multi-sensory Remote Sensing Data: Machine Learning Perspective for Satellite Images. In Artificial Intelligence Perspectives and Applications; Silhavy, R., Senkerik, R., Oplatkova, Z.K., Prokopova, Z., Silhavy, P., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 333–346. [Google Scholar]
- Oommen, T.; Misra, D.; Twarakavi, N.K.C.; Prakash, A.; Sahoo, B.; Bandopadhyay, S. An Objective Analysis of Support Vector Machine Based Classification for Remote Sensing. Math Geosci. 2008, 40, 409–424. [Google Scholar] [CrossRef]
- Gómez, C.; White, J.C.; Wulder, M.A. Optical remotely sensed time series data for land cover classification: A review. ISPRS J. Photogramm. Remote Sens. 2016, 116, 55–72. [Google Scholar] [CrossRef]
- Wozniak, M.; Graña, M.; Corchado, E. A survey of multiple classifier systems as hybrid systems. Inf. Fusion 2014, 16, 3–17. [Google Scholar] [CrossRef]
- Kuncheva, L.I. Combining Pattern Classifiers: Methods and Algorithms; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2004. [Google Scholar]
- Gopinath, B.; Shanthi, N. Development of an Automated Medical Diagnosis System for Classifying Thyroid Tumor Cells using Multiple Classifier Fusion. Technol. Cancer Res. Treat. 2014, 14, 653–662. [Google Scholar] [CrossRef] [PubMed]
- Li, H.; Shen, F.; Shen, C.; Yang, Y.; Gao, Y. Face Recognition Using Linear Representation Ensembles. Pattern Recognit. 2016, 59, 72–87. [Google Scholar] [CrossRef]
- Lumini, A.; Nanni, L.; Brahnam, S. Ensemble of texture descriptors and classifiers for face recognition. Appl. Comput. Inform. 2016, 13, 79–91. [Google Scholar] [CrossRef]
- Clinton, N.; Yu, L.; Gong, P. Geographic stacking: Decision fusion to increase global land cover map accuracy. ISPRS J. Photogramm. Remote Sens. 2015, 103, 57–65. [Google Scholar] [CrossRef]
- Lijun, D.; Chuang, L. Research on remote sensing image of land cover classification based on multiple classifier combination. Wuhan Univ. J. Nat. Sci. 2011, 16, 363–368. [Google Scholar]
- Li, D.; Yang, F.; Wang, X. Study on Ensemble Crop Information Extraction of Remote Sensing Images Based on SVM and BPNN. J. Indian Soc. Remote Sens. 2016, 45, 229–237. [Google Scholar] [CrossRef]
- Du, P.; Xia, J.; Zhang, W.; Tan, K.; Liu, Y.; Liu, S. Multiple classifier system for remote sensing image classification: A review. Sensors (Basel) 2012, 12, 4764–4792. [Google Scholar] [CrossRef] [PubMed]
- Gargiulo, F.; Mazzariello, C.; Sansone, C. Multiple Classifier Systems: Theory, Applications and Tools. In Handbook on Neural Information Processing; Bianchini, M., Maggini, M., Jain, L.C., Eds.; Springer: Berlin/Heidelberg, Germany, 2013; Volume 49, pp. 505–525. [Google Scholar]
- Corrales, D.C.; Figueroa, A.; Ledezma, A.; Corrales, J.C. An Empirical Multi-classifier for Coffee Rust Detection in Colombian Crops. In Proceedings of the Computational Science and Its Applications—ICCSA 2015: 15th International Conference, Banff, AB, Canada, 22–25 June 2015; Gervasi, O., Murgante, B., Misra, S., Gavrilova, L.M., Rocha, C.A.M.A., Torre, C., Taniar, D., Apduhan, O.B., Eds.; Springer International Publishing: Cham, Switzerland, 2015; pp. 60–74. [Google Scholar]
- Song, X.; Pavel, M. Performance Advantage of Combined Classifiers in Multi-category Cases: An Analysis. In Proceedings of the 11th International Conference, ICONIP 2004, Calcutta, India, 22–25 November 2004; pp. 750–757. [Google Scholar]
- Polikar, R. Ensemble based systems in decision making. Circuits Syst. Mag. IEEE 2006, 6, 21–45. [Google Scholar] [CrossRef]
- Duin, R.P.W. The Combining Classifier: To Train or Not to Train? In Proceedings of the 16th International Conference on Pattern Recognition, Quebec City, QC, Canada, 11–15 August 2002.
- Joint Experiment for Crop Assessment and Monitoring (JECAM). Mali JECAM Study Site, Mali-Koutiala—Site Description. Available online: http://www.jecam.org/?/site-description/mali (accessed on 18 April 2018).
- Stratoulias, D.; de By, R.A.; Zurita-Milla, R.; Retsios, V.; Bijker, W.; Hasan, M.A.; Vermote, E. A Workflow for Automated Satellite Image Processing: From Raw VHSR Data to Object-Based Spectral Information for Smallholder Agriculture. Remote Sens. 2017, 9, 1048. [Google Scholar] [CrossRef]
- Rouse, W.; Haas, R.H.; Deering, D.W. Monitoring vegetation systems in the great plains with ERTS. Proc. Earth Resour. Technol. Satell. Symp. NASA 1973, 1, 309–317. [Google Scholar]
- Louhaichi, M.; Borman, M.M.; Johnson, D.E. Spatially located platform and aerial photography for documentation of grazing impacts on wheat. Geocarto Int. 2001, 16, 65–70. [Google Scholar] [CrossRef]
- Huete, A.; Didan, K.; Miura, T.; Rodriguez, E.P.; Gao, X.; Ferreira, L.G. Overview of the radiometric and biophysical performance of the MODIS vegetation indices. Remote Sens. Environ. 2002, 83, 195–213. [Google Scholar] [CrossRef]
- Huete, A.R. A Soil-Adjusted Vegetation Index (SAVI). Remote Sens. Environ. 1988, 25, 295–309. [Google Scholar] [CrossRef]
- Qi, J.; Chehbouni, A.; Huete, A.R.; Kerr, Y.H.; Sorooshian, S. A modified soil adjusted vegetation index. Remote Sens. Environ. 1994, 48, 119–126. [Google Scholar] [CrossRef]
- Haboudane, D.; Miller, J.R.; Tremblay, N.; Zarco-Tejada, P.J.; Dextraze, L. Integrated narrow-band vegetation indices for prediction of crop chlorophyll content for application to precision agriculture. Remote Sens. Environ. 2002, 81, 416–426. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Kaufman, Y.J.; Stark, R.; Rundquist, D. Novel algorithms for remote estimation of vegetation fraction. Remote Sens. Environ. 2002, 80, 76–87. [Google Scholar] [CrossRef]
- Haralick, R.; Shanmugan, K.; Dinstein, I. Textural features for image classification. IEEE Trans. Syst. Man Cybern. 1973, 3, 610–621. [Google Scholar] [CrossRef]
- Conners, R.W.; Trivedi, M.M.; Harlow, C.A. Segmentation of a high-resolution urban scene using texture operators. Comput. Vis. Graph. Image Process. 1984, 25, 273–310. [Google Scholar] [CrossRef]
- Gorelick, N.; Hancher, M.; Dixon, M.; Ilyushchenko, S.; Thau, D.; Moore, R. Google Earth Engine: Planetary-scale geospatial analysis for everyone. Remote Sens. Environ. 2017, 202, 18–27. [Google Scholar] [CrossRef]
- Izquierdo-Verdiguier, E.; Zurita-Milla, R.; de By, R.A. On the use of guided regularized random forests to identify crops in smallholder farm fields. In Proceedings of the 2017 9th International Workshop on the Analysis of Multitemporal Remote Sensing Images (MultiTemp), Brugge, Belgium, 27–29 June 2017; pp. 1–3. [Google Scholar]
- Breiman, L. Random forests. Mach. Learn. 2001, 45, 5–32. [Google Scholar] [CrossRef]
- Phillips, S.J.; Anderson, R.P.; Schapire, R.E. Maximum entropy modeling of species geographic distributions. Ecol. Model. 2006, 190, 231–259. [Google Scholar] [CrossRef]
- Cortes, C.; Vapnik, V. Support Vector Networks. Mach. Learn. 1995, 20, 273–297. [Google Scholar] [CrossRef]
- Duro, D.C.; Franklin, S.E.; Dubé, M.G. A comparison of pixel-based and object-based image analysis with selected machine learning algorithms for the classification of agricultural landscapes using SPOT-5 HRG imagery. Remote Sens. Environ. 2012, 118, 259–272. [Google Scholar] [CrossRef]
- Gao, T.; Zhu, J.; Zheng, X.; Shang, G.; Huang, L.; Wu, S. Mapping spatial distribution of larch plantations from multi-seasonal landsat-8 OLI imagery and multi-scale textures using random forests. Remote Sens. 2015, 7, 1702–1720. [Google Scholar] [CrossRef]
- Pal, M. Random forest classifier for remote sensing classification. Int. J. Remote Sens. 2005, 26, 217–222. [Google Scholar] [CrossRef]
- Rodriguez-Galiano, V.F.; Ghimire, B.; Rogan, J.; Chica-Olmo, M.; Rigol-Sanchez, J.P. An assessment of the effectiveness of a random forest classifier for land-cover classification. ISPRS J. Photogramm. Remote Sens. 2012, 67, 93–104. [Google Scholar] [CrossRef]
- Nitze, I.; Schulthess, U.; Asche, H. Comparison of Machine Learning Algorithms Random Forest, Artificial Neural Network and Support Vector Machine to Maximum Likelihood for Supervised Crop Type Classification. In Proceedings of the 4th international conference on Geographic Object-Based Image Analysis (GEOBIA) Conference, Rio de Janeiro, Brazil, 7–9 May 2012; pp. 35–40. [Google Scholar]
- Akar, O.; Güngör, O. Integrating multiple texture methods and NDVI to the Random Forest classification algorithm to detect tea and hazelnut plantation areas in northeast Turkey. Int. J. Remote Sens. 2015, 36, 442–464. [Google Scholar] [CrossRef]
- Berger, A.L.; della Pietra, S.A.; della Pietra, V.J. A Maximum Entropy Approach to Natural Language Process. Comput. Linguist. 1996, 22, 39–71. [Google Scholar]
- Evangelista, P.H.; Stohlgren, T.J.; Morisette, J.T.; Kumar, S. Mapping Invasive Tamarisk (Tamarix): A Comparison of Single-Scene and Time-Series Analyses of Remotely Sensed Data. Remote Sens. 2009, 1, 519–533. [Google Scholar] [CrossRef]
- Rahmati, O.; Pourghasemi, H.R.; Melesse, A.M. Application of GIS-based data driven random forest and maximum entropy models for groundwater potential mapping: A case study at Mehran Region, Iran. Catena 2016, 137, 360–372. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Remote Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Izquierdo-Verdiguier, E.; Gómez-Chova, L.; Camps-Valls, G. Kernels for Remote Sensing Image Classification. In Wiley Encyclopedia of Electrical and Electronics Engineering; John Wiley & Sons, Inc.: Hoboken, NJ, USA, 2015; pp. 1–23. [Google Scholar]
- Kohavi, R. A study of cross-validation and bootstrap for accuracy estimation and model selection. Int. Jt. Conf. Artif. Intell. 1995, 1137–1143. [Google Scholar]
- Smits, P.C. Multiple classifier systems for supervised remote sensing image classification based on dynamic classifier selection. IEEE Trans. Geosci. Remote Sens. 2002, 40, 801–813. [Google Scholar] [CrossRef]
- Kavzoglu, T.; Colkesen, I. A kernel functions analysis for support vector machines for land cover classification. Int. J. Appl. Earth Obs. Geoinf. 2009, 11, 352–359. [Google Scholar] [CrossRef]
- Hao, P.; Wang, L.; Niu, Z. Comparison of Hybrid Classifiers for Crop Classification Using Normalized Difference Vegetation Index Time Series: A Case Study for Major Crops in North Xinjiang, China. PLoS ONE 2015, 10, e0137748. [Google Scholar] [CrossRef] [PubMed]
- Amici, V.; Marcantonio, M.; la Porta, N.; Rocchini, D. A multi-temporal approach in MaxEnt modelling: A new frontier for land use/land cover change detection. Ecol. Inform. J. 2017, 40, 40–49. [Google Scholar] [CrossRef]
- Gilmore, R.P., Jr.; Millones, M. Death to Kappa: Birth of quantity disagreement and allocation disagreement for accuracy assessment. Int. J. Remote Sens. 2011, 32, 4407–4429. [Google Scholar]








| Vegetation Index (VI) | Formula |
|---|---|
| Normalized Difference Vegetation Index (NDVI) [44] | (NIR − R)/(NIR + R) |
| Green Leaf Index (GLI) [45] | (2 × G − R − B)/(2 × G + R + B) |
| Enhanced Vegetation Index (EVI) [46] | EVI = 2.5 × (NIR −R)/(NIR +6 × R − 7.5 × B + 1) |
| Soil Adjusted Vegetation Index (SAVI) [47] | (1 + L) × (NIR − R)/(NIR + R+ L), where L = 0.5 |
| Modified Soil Adjusted Vegetation Index (MSAVI) [48] | |
| Transformed Chlorophyll Absorption in Reflectance Index (TCARI) [49] | 3 × ((RE − R) − 0.2 × (RE − G) × (RE/R)) |
| Visible Atmospherically Resistance Index (VARI) [50] | (G − R)/(G + R − B) |
| Feature | Features Per Image | Total Per Image Series |
|---|---|---|
| Spectral bands | 7 | 49 |
| Vegetation indices | 7 | 49 |
| GLCM-based features applied to image bands | 126 | 882 |
| Total | 140 | 980 |
| Image Date | ||||||
|---|---|---|---|---|---|---|
| 22 May 2014 | 30 May 2014 | 26 June 2014 | 29 July 2014 | 18 October 2014 | 1 November 2014 | 14 November 2014 |
| b3 | b3_savg | b4_diss | b3 | SAVI | b3_diss | b2 |
| b7 | b5_savg | b5_dvar | b5_savg | VARI | b4_dvar | b2_savg |
| b8 | b6_corr | b8_ent | b6 | b4_idm | b3_dvar | |
| b8_idm | b7_idm | GLI | b6_corr | b4_savg | b8 | |
| b7_savg | MSAVI | b6_savg | b6 | EVI | ||
| b8_savg | TCARI | b8_diss | b6_savg | TCARI | ||
| VARI | b7_corr | |||||
| b7_savg | ||||||
| b8_diss | ||||||
| b8_savg | ||||||
| EVI | ||||||
| GLI | ||||||
| TCARI | ||||||
| VARI | ||||||
| Class | Crop Name | # Pixels | |
|---|---|---|---|
| Training | Testing | ||
| 1 | Maize | 395 | 234 |
| 2 | Millet | 531 | 309 |
| 3 | Peanut | 276 | 168 |
| 4 | Sorghum | 472 | 291 |
| 5 | Cotton | 455 | 256 |
| Total | 2129 | 1258 | |
| OA | Kappa | ||||||||
|---|---|---|---|---|---|---|---|---|---|
| Classifier | Mean | Std | Min | Max | Mean | Std | Min | Max | |
| Base Classifier | MaxEnt | 0.5975 | 0.0078 | 0.5874 | 0.6105 | 0.4913 | 0.0098 | 0.4785 | 0.5070 |
| RF | 0.7172 | 0.0041 | 0.7107 | 0.7234 | 0.6412 | 0.0050 | 0.6333 | 0.6480 | |
| SVML | 0.6176 | 0.0095 | 0.6010 | 0.6335 | 0.5165 | 0.0119 | 0.4958 | 0.5361 | |
| SVMP | 0.6951 | 0.0092 | 0.6852 | 0.7154 | 0.6151 | 0.0114 | 0.6029 | 0.6401 | |
| SVMR | 0.7069 | 0.0048 | 0.6963 | 0.7154 | 0.6294 | 0.0058 | 0.6172 | 0.6398 | |
| Ensemble | Voting | 0.7348 | 0.0060 | 0.7059 | 0.7464 | 0.6642 | 0.0075 | 0.6279 | 0.6788 |
| WVoting | 0.7506 | 0.0060 | 0.7234 | 0.7607 | 0.6841 | 0.0076 | 0.6497 | 0.6969 | |
| Maize | Millet | Peanut | Sorghum | Cotton | PA | |
|---|---|---|---|---|---|---|
| Maize | 140 | 30 | 5 | 44 | 15 | 0.5983 |
| Millet | 14 | 239 | 16 | 33 | 7 | 0.7735 |
| Peanut | 10 | 17 | 109 | 24 | 8 | 0.6488 |
| Sorghum | 18 | 23 | 8 | 224 | 18 | 0.7698 |
| Cotton | 13 | 26 | 6 | 21 | 190 | 0.7422 |
| Maize | Millet | Peanut | Sorghum | Cotton | PA | |
|---|---|---|---|---|---|---|
| Maize | 167 | 23 | 3 | 32 | 9 | 0.7137 |
| Millet | 19 | 243 | 13 | 28 | 6 | 0.7864 |
| Peanut | 5 | 19 | 120 | 21 | 3 | 0.7143 |
| Sorghum | 21 | 16 | 6 | 230 | 18 | 0.7904 |
| Cotton | 17 | 25 | 4 | 15 | 195 | 0.7617 |
| Maize | Millet | Peanut | Sorghum | Cotton | PA | |
|---|---|---|---|---|---|---|
| Maize | 163 | 25 | 3 | 34 | 9 | 0.6966 |
| Millet | 18 | 245 | 13 | 27 | 6 | 0.7929 |
| Peanut | 5 | 21 | 117 | 22 | 3 | 0.6964 |
| Sorghum | 22 | 13 | 7 | 229 | 20 | 0.7869 |
| Cotton | 18 | 24 | 4 | 15 | 195 | 0.7617 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Aguilar, R.; Zurita-Milla, R.; Izquierdo-Verdiguier, E.; A. de By, R. A Cloud-Based Multi-Temporal Ensemble Classifier to Map Smallholder Farming Systems. Remote Sens. 2018, 10, 729. https://doi.org/10.3390/rs10050729
Aguilar R, Zurita-Milla R, Izquierdo-Verdiguier E, A. de By R. A Cloud-Based Multi-Temporal Ensemble Classifier to Map Smallholder Farming Systems. Remote Sensing. 2018; 10(5):729. https://doi.org/10.3390/rs10050729
Chicago/Turabian StyleAguilar, Rosa, Raul Zurita-Milla, Emma Izquierdo-Verdiguier, and Rolf A. de By. 2018. "A Cloud-Based Multi-Temporal Ensemble Classifier to Map Smallholder Farming Systems" Remote Sensing 10, no. 5: 729. https://doi.org/10.3390/rs10050729
APA StyleAguilar, R., Zurita-Milla, R., Izquierdo-Verdiguier, E., & A. de By, R. (2018). A Cloud-Based Multi-Temporal Ensemble Classifier to Map Smallholder Farming Systems. Remote Sensing, 10(5), 729. https://doi.org/10.3390/rs10050729