Next Article in Journal
Remotely Sensing the Morphometrics and Dynamics of a Cold Region Dune Field Using Historical Aerial Photography and Airborne LiDAR Data
Next Article in Special Issue
Using InSAR Coherence for Investigating the Interplay of Fluvial and Aeolian Features in Arid Lands: Implications for Groundwater Potential in Egypt
Previous Article in Journal
An Image Fusion Method Based on Image Segmentation for High-Resolution Remotely-Sensed Imagery
Previous Article in Special Issue
Water Loss Due to Increasing Planted Vegetation over the Badain Jaran Desert, China
 
 
Search for Articles:
Title / Keyword
Author / Affiliation / Email
Journal
Article Type
 
 
Advanced Search
 
Section
Special Issue
Volume
Issue
Number
Page
 
Journals
Remote Sensing
Volume 10
Issue 5
10.3390/rs10050791
remotesensing-logo
Submit to this Journal Review for this Journal Propose a Special Issue
► Article Menu

Article Menu

share Share announcement Help format_quote Cite question_answer Discuss in SciProfiles thumb_up
...
Endorse textsms
...
Comment
first_page
settings
Order Article Reprints
Font Type:
Arial Georgia Verdana
Font Size:
Aa Aa Aa
Line Spacing:
Column Width:
Background:
Article

Spatiotemporal Analysis of Landsat-8 and Sentinel-2 Data to Support Monitoring of Dryland Ecosystems

by
Neal J. Pastick
1,2,*,
Bruce K. Wylie
3 and
Zhuoting Wu
4
1
Stinger Ghaffarian Technologies, Inc., contractor to the U.S. Geological Survey, Sioux Falls, SD 57198, USA
2
Department of Forest Resources, University of Minnesota, St. Paul, MN 55108, USA
3
U.S. Geological Survey, Earth Resources Observation and Science Center, Sioux Falls, SD 57198, USA
4
U.S. Geological Survey, National Land Imaging Program, Flagstaff, AZ 86001, USA
*
Author to whom correspondence should be addressed.
Remote Sens. 2018, 10(5), 791; https://doi.org/10.3390/rs10050791
Submission received: 11 April 2018 / Revised: 4 May 2018 / Accepted: 17 May 2018 / Published: 19 May 2018
(This article belongs to the Special Issue Remote Sensing of Arid/Semiarid Lands)
Browse Figures
Versions Notes

Abstract

:
Drylands are the habitat and source of livelihood for about two fifths of the world’s population and are highly susceptible to climate and anthropogenic change. To understand the vulnerability of drylands to changing environmental conditions, land managers need to effectively monitor rates of past change and remote sensing offers a cost-effective means to assess and manage these vast landscapes. Here, we present a novel approach to accurately monitor land-surface phenology in drylands of the Western United States using a regression tree modeling framework that combined information collected by the Operational Land Imager (OLI) onboard Landsat 8 and the Multispectral Instrument (MSI) onboard Sentinel-2. This highly-automatable approach allowed us to precisely characterize seasonal variations in spectral vegetation indices with substantial agreement between observed and predicted values (R2 = 0.98; Mean Absolute Error = 0.01). Derived phenology curves agreed with independent eMODIS phenological signatures of major land cover types (average r-value = 0.86), cheatgrass cover (average r-value = 0.96), and growing season proxies for vegetation productivity (R2 = 0.88), although a systematic bias towards earlier maturity and senescence indicates enhanced monitoring capabilities associated with the use of harmonized Landsat-8 Sentinel-2 data. Overall, our results demonstrate that observations made by the MSI and OLI can be used in conjunction to accurately characterize land-surface phenology and exclusion of imagery from either sensor drastically reduces our ability to monitor dryland environments. Given the declines in MODIS performance and forthcoming decommission with no equivalent replacement planned, data fusion approaches that integrate observations from multispectral sensors will be needed to effectively monitor dryland ecosystems. While the synthetic image stacks are expected to be locally useful, the technical approach can serve a wide variety of applications such as invasive species and drought monitoring, habitat mapping, production of phenology metrics, and land-cover change modeling.

Graphical Abstract

1. Introduction

Drylands occupy approximately 41% of Earth’s land surface and are currently home to over 38% of the world’s population [1]. Consequently, drylands exert significant controls on socio-environmental systems, including global energy, water, and carbon cycles [2]. Enhanced warming has promoted dryland expansion throughout portions of the world [3], by increasing evaporative demand and decreasing soil moisture, and strongly modifies the capacity of dryland ecosystems to sequester carbon through vegetation shifts and warming effects on photosynthesis and decomposition [4]. The spread of cheatgrass (Bromus tectorum L.) has also negatively impacted biodiversity and productivity of drylands in the western United States [5]. Because vegetation dynamics exert a strong control on water, energy, and biogeochemical budgets in drylands [6], knowledge of land-surface phenology is vital for effectively monitoring dryland ecosystems and is important for both the research community and the policy community in the management of Earth’s landscapes. Here, land-surface phenology is defined as the spatiotemporal development of vegetated land surfaces as imaged by spaceborne sensors.
Satellite data provide a cost-effective means for understanding land-surface phenology and vegetation characteristics across large areas. For example, Moderate Resolution Image Spectroradiometer (MODIS) data have been used to estimate vegetation type and biomass, leaf area index, primary productivity, and biophysical variables that influence climate [7,8,9]. Likewise, Landsat data have been used to characterize global-scale processes such as changes in forest cover [10] and surface waters [11] at unprecedented scales. Free and open access of the Landsat archive has resulted in a deluge of new methods and data products in phenological research [12,13]. However, the low temporal availability of Landsat data, due in large part to cloud and shadow coverage, continues to be a major barrier for monitoring phenology and land-cover change [14].
To overcome data availability issues, Landsat data have been fused with information collected by satellites with higher temporal resolution (e.g., MODIS) to create high-temporal, cloud-free time series [15,16,17]. Likewise, Landsat images from multiple years (and sensors) can be merged into a single time series, but such methods need to consider inter-annual differences in phenology, land surface changes, and different sensor characteristics [14,18]. More recently, data collected by the Operational Landsat Imagery (OLI) onboard Landsat-8 have been fused with freely-available information collected by the Multispectral Instrument (MSI) onboard Sentinel-2 [19]. The combination of MSI and OLI data provides a global mean revisit interval of approximately five days [20], thereby substantially increasing monitoring capabilities of the Earth’s surface, but few studies have proposed methodologies for integrating these datasets to provide cloud-free surface observations and time series data needed to monitor Earth’s surface.
Here, we integrate OLI and MSI data into a novel, regression tree modeling framework to develop spatially-explicit estimates of Landsat-like Normalized Difference Vegetation Index (NDVI) throughout an arid and semi-arid environment in the Western United States. Model results were compared to observations of land and cheatgrass cover and independent data collected by the MODIS onboard Aqua. In doing so, we address the following questions: (1) Are surface reflectance data from Landsat-8 OLI and Sentinel-2 MSI data comparable in this region? (2) Can Landsat-8 OLI and Sentinel-2 MSI data be used in conjunction to accurately characterize seasonal vegetation index signatures within dryland environments? (3) To what extent does excluding MSI data impact our ability to effectively monitor land-surface phenology in drylands? This research fills a critical gap in the understanding of current monitoring capabilities of arid and semi-arid environments that cover a substantial portion of the globe. Findings are relevant to future land imaging missions (e.g., Landsat 10) and are useful for understanding key requirements and attributes needed to effectively monitor water-limited ecosystems.

2. Data and Study area

2.1. Study Area

Our analysis considers a single Harmonized Landsat-8 Sentinel-2 (HLS) tile (11SQD; https://hls.gsfc.nasa.gov/) located in Utah and Nevada, USA representing approximately 12,000 km2 or 14M pixels (30-m spatial resolution) (Figure 1). The study area is dominated by shrub/scrubs (68%), followed by evergreen forests (19%), bare ground (5%), grassland/herbaceous (5%), and pasture/hay (1%) land cover according to the 2011 National Land Cover Database (NLCD; [21]). PRISM climate normals (1981–2010) indicate that the average temperature and total precipitation range from −2 to 11 °C and from 160 to 810 mm, respectively, largely reflecting local elevation differences (1339–3781 m). Cheatgrass is relatively common in the lowlands of the study area [22].

2.2. Harmonized Landsat-8 Sentinel-2 Data

Harmonized Landsat-Sentinel-2 (HLS) data were used in this study and are consistent surface reflectance products derived from observations made by the Multispectral Instrument (MSI) onboard Sentinel-2 and the Operational Land Imager (OLI) onboard Landsat 8. The HLS products were generated using orthorectified top-of-atmosphere (TOA) reflectance data and have undergone atmospheric correction, geometric resampling (e.g., 30 m spatial resolution), geographic registration, BRDF normalization, and band-pass adjustments have been made to MSI data. Readers are referred to the product user’s guide for a full description of the HLS data processing [23]. Only data from Weeks 9 (start date 6 March 2016) to 47 (end date 24 November 2016) were considered in our analysis to avoid periods of snow cover and to capture the entire growing season.

2.3. eMODIS Data

The 250 m expedited MODIS (eMODIS) weekly NDVI composites [24] were used in this study to facilitate comparisons with derived growing season phenology. The eMODIS NDVI composites used data quality information to minimize errors associated with clouds, view angles and snow observation for each weekly NDVI composite. Reference [7] found degradation in MODIS Collect 5 Terra NDVI after about 2007 so MODIS Aqua Collect 6 data were used in this study. Instability in the Collect 6 surface reflectance, often associated with low red reflectance, caused sporadic ephemeral spikes in NDVI. We developed an algorithm to identify these erroneous NDVI spikes and treat them as cloud contaminated pixels. The de-spike algorithm flagged weekly NDVI values as cloud contaminated if the current week NDVI was at least ten percent greater than the maximum NDVI from the prior and post two weeks, and the difference from the current NDVI and both the prior and post weekly NDVI values was greater than 20%. The weekly NDVI time series data were temporally smoothed (five-week) to interpolate NDVI values across ephemeral drops typically associated with cloudy weeks [25], but the raw data and associated quality masks were used within cross-correlation analysis because smoothing and different data observation densities can shift resulting phenocurves. To facilitate eMODIS comparisons with modeled NDVI (see Section 3.3.2), weekly eMODIS NDVI values were downscaled to 30-m using approaches based on regression tree models that are developed at a 250 m resolution (Landsat NDVI is averaged up to 250 m resolution) to predict eMODIS 250-m NDVI from Landsat imagery [17,26]. Regression tree models are then applied to the original 30 m Landsat spectral band data to produce an eMODIS equivalent NDVI image at the 30 m resolution.

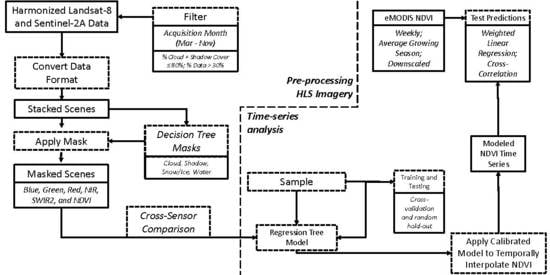
3. Methods

The overall workflow for our analysis consisted of ten different steps (Figure 2) with two major components (i.e., pre-processing and time-series analysis). Pre-processing consisted of filtering imagery using standard quality metrics (i.e., cloud and shadow cover ≤ 80%, and data quality > 30%) and date of year (May–September 2016), applying image masks created by decision tree models, and cross-sensor comparisons. Time series analysis consisted of regression tree model calibration and validation for the interpolation of multi-spectral indices calculated from HLS data. Time-series predictions were compared to independent information derived from eMODIS data and estimates of cheatgrass cover to ensure phenology curves were logical. Specific details for each processing step are discussed below.

3.1. Data Masks

The mask layers distributed with the HLS data, as created using the FMask algorithm [27] and the Landsat 8 Surface Reflectance Code (LaSRC) cloud masking algorithm [28], were of insufficient quality for our time series analysis due to their inability to differentiate common features from others (i.e., playas from clouds and shadows from evergreen trees; Figure 3). This was particularly apparent for Landsat masks despite the use of the cirrus and thermal bands in the LaSRC cloud masking algorithm [29]. Subsequently, we developed separate decision tree models for MSI and OLI data trained on about two million data points (distributed through space and time) to develop robust masks for clouds, shadows, water, and snow/ice pixels. Decision tree models were developed using a commercial version of the See5 software (See5: An Informal Tutorial, 27 December 2017, http://rulequest.com/see5-win.html) and validated using random hold-out samples (20%). Calibrated models were then applied to each image to mask irrelevant data. The accuracies of the masks were assessed using a random-hold out sample of interpretations of cloud, shadows, water, snow/ice that were distributed through space and time. Independent interpretations and masking layers were used to construct confusion matrices to compute overall and class specific accuracies.

3.2. Cross-Sensor Calibration

We compared the radiometric characteristics of HLS bands using one-day-apart images acquired over the study area, to ensure HLS band-pass adjustments were of sufficient quality for our analysis. Small time differences reduce uncertainties related to radiometric bias caused by external factors. The selected MSI and OLI image pairs (Table 1) were generally unaffected by clouds and were further screened using masks developed for this study. We sampled approximately 50,000 different pixels across the site and compared surface reflectance data from equivalent bands (i.e., blue, green, red, near-infrared (NIR), and short-wave infrared (SWIR) 2) and the normalized difference vegetation index (NDVI) calculated using Equation (1) and bands B8A and B04 for MSI imagery as suggested by others [30].
NDVI = NIR − Red NIR + Red

3.3. Time-Series Analysis

3.3.1. Database Development and Modeling

Model development and testing databases were constructed by equally sampling the range of observed, mean NDVI values throughout the study period, where approximately 50,000 pixels were randomly selected and repeatedly sampled for each acquisition date. Spatial coordinates, Julian Day, and HLS-NDVI data served as explanatory variables within our modeling framework. Masked pixels were flagged as missing values in the modeling databases and retained their raw values within the imagery. Likewise, NDVI data calculated from OLI imagery were assumed missing for time steps when the values were used as the dependent variable, to avoid circularity that would result in a perfect prediction. The inclusion of spatial coordinates and day of year (Julian Day) information insured that spatial and temporal autocorrelation effects were minimized. The functional form of the model, for one case or period, can be written as:
NDVIt64 (OLI) = f (Location, Julian Day, NDVIt77…t327)
where t is time or Julian Day.
Two sets of models were developed to predict NDVI throughout the study period, one including and excluding MSI data as an independent variable (ModelLS and ModelL), using a boosted regression tree ensemble approach and the commercial version of the C4.5 algorithm [31]. Regression trees are nonparametric models that hierarchically subdivide data using a set of conditional rules, while minimizing an objective function (e.g., Mean Absolute Error (MAE)), and fit linear regression models in each subspace. Regression tree models can approximate any function of a continuous variable, can handle missing data, and have been used for time series prediction [32]. Model calibration and testing was done using cross-validation procedures and a random-hold out sample (20%), respectively. After model calibration, the rules and associated linear equations were applied to the environmental covariates to develop spatially-explicit estimates (30-m spatial resolution) of Landsat equivalent, or modeled, NDVI at weekly intervals throughout the study period.

3.3.2. Product Comparisons

Weekly normalized difference vegetation index (NDVI) data, as predicted from the regression tree models, were compared to: (1) the weekly 250-m time series of masked eMODIS data using cross-correlation analysis (i.e., 1-to-1 mapping and lagged); (2) average growing season (April–September) NDVI (250-m) calculated from the smoothed eMODIS time series; and (3) downscaled (30-m) eMODIS products (NDVI at Weeks 22 and 23) using weighted least square regression analysis. Weekly eMODIS and predicted NDVI data were summarized and compared for major land cover types ([21]; resampled to 250-m using nearest neighbor interpolation) and percentage cheatgrass cover prediction (250-m) made throughout the study area [22], to determine if the modeled data could logically capture land-surface dynamics throughout the growing season. The average growing season NDVI was computed from each dataset and compared at the native spatial resolution of the reference datasets (i.e., 250-m) using weighted (by the inverse of the coefficient of variation calculated using 3 × 3 moving window approach on the reference dataset) least squares regression analysis for about 10,000 pixels distributed throughout the study area. These comparisons were conducted using weekly interpolations by models with and without Sentinel-2A data, to assess the added benefits of including Sentinel data in the modeling framework. Statistical metrics (i.e., Adjusted R2, MAE, relative MAE, and Root Mean Square Error (RMSE)) were used to determine agreement and assess model performance.

4. Results

4.1. Data Masks

The overall accuracy for both decision tree masking models (i.e., OLI and MSI) was above 99%, with similar commission and omission error rates, despite that lack of cirrus and thermal bands in MSI data (Table 2). These accuracy metrics far exceed those of the HLS mask layers, as calculated from a subset of these interpretations made on three dates of imagery for each sensor, where OLI and MSI masks (converted to binary) had an overall accuracy of 76% and 89%, respectively (Table S1).

4.2. Cross-Sensor Calibration

Analysis of one-day-apart acquisitions (Figure 4) showed strong 1:1 agreement for NDVI, blue, green, red, and near-infrared bands (R2 from 0.89 to 0.98), with minor bias only observed in short-wave infrared 2 spectrum (R2 = 0.95), after accounting for contaminated pixels (i.e., cloud, shadow, snow, and water). This suggests that Sentinel-2 MSI data can be used in conjunction with Landsat-8 OLI data, without further band-pass adjustments, with minimal impacts on NDVI time series analysis discussed below.

4.3. Time-Series Analysis

Overall, there was a very strong correlation (R2 = 0.99) between ModelLS predictions and randomly-withheld Landsat-NDVI observations, with little difference in error metrics for each acquisition date (Table 3). Correlations between observed and predicted values were lowest (R2 > 0.92) for the first time step (model not constrained by data prior to Day of Year 64) and for three consecutive acquisitions dates (i.e., Day of Year 112–144) with high cloud and shadow cover (R2 = 0.96). There was little to no decrease in predictive performance when Sentinel-2 MSI data were excluded as an explanatory variable during ModelL development (Table S2). While ModelL performs well on withheld Landsat observation throughout the year, this does not necessarily mean it accurately characterizes greenness curves throughout the entire year, as is demonstrated below.
We found strong correlations between modeled NDVI and coarser eMODIS observations for major land cover types in the study area (Figure 5), with substantially higher agreement between ModelLS and eMODIS time series, as compared to estimates made by ModelL. The poorest agreement between ModelLS and eMODIS NDVI (r-value of 0.67) correspond to time series in barren land cover types that are subject to water impoundment, as was identified from the time series data. The highest agreements occurred in Shrub/Scrub and Evergreen Forests (r-value = 0.94), followed by Pasture/Hay (0.92), and Grassland/Herbaceous (0.83) land cover types. Interestingly, ModelLS NDVI values peaked earlier (~2 weeks) than eMODIS values for grasslands and shrubs, although the maximum correlation was obtained using 1-to-1 mapping. Agreement between eMODIS and ModelL estimates were highest for Evergreen Forests (r-value = 0.63), followed by Barren (0.59), Pasture/Hay (0.55), Grassland/Herbaceous (0.49), and Shrub/Scrub (0.19).
When estimates are stratified by percentage cheatgrass cover across the entire study area, we find good agreement between ModelLS and eMODIS time series data, where peak NDVI and similarity metrics vary as a function of percentage cheatgrass cover (Figure 6). That is, maximum correlations were found for sites with low (r-value = 0.95), moderate (0.96), and high cheatgrass cover (0.98) assuming no lag. Conversely, there was very poor agreement between ModelL and eMODIS time series data within low (r-value = 0.10), moderate (0.14), and high cheatgrass cover (0.33) (Figure 6).
When estimates are averaged across growing season months, we find substantially higher agreement between ModelLS and eMODIS values, as compared to ModelL estimates (R2 = 0.88 versus R2 = 0.72; Figure 7). We also found much higher agreement between weekly eMODIS and interpolated data (ModelLS) for two weeks (Weeks 22 and 23) during peak-growing season, as compared to downscaled eMODIS products (Figure 8). The slight lag between eMODIS and modeled NDVI data are manifested in this comparison as a systematically low bias for modeled NDVI during these growing season weeks.

5. Discussion

In this research, we presented a novel approach to accurately monitor land-surface phenology and generate spatially-explicit estimates of surface reflectance data using a regression tree modeling framework that combined information collected by Landsat OLI and Sentinel MSI. Overall, we found that data collected from these sensors were largely compatible, but the extent to which HLS pre-processing ensured compatibility is outside the scope of this study. To effectively characterize seasonal vegetation index curves, we developed robust cloud masks because HLS masking products were of insufficient quality. For a thorough review of operational cloud masking algorithms and their associated performance, we refer readers to reference [29]. We demonstrate that the inclusion of Sentinel MSI data into our modeling framework substantially improves our ability to track and represent land-surface dynamics in water-limited environments, due in large part to the fact that additional observations allow us to seamlessly fill observational gaps due to clouds and shadows.
Our methodology has advantages over previously published approaches and is highly automatable. First, our approach explicitly mitigates spatial and temporal autocorrelation effects, by integrating spatial and temporal covariates (i.e., latitude, longitude, Julian date, and spectral reflectance from other dates) directly into the global model, which per-pixel approaches typically ignore (e.g., [14,33]). This is particularly import for monitoring semi-arid environments because vegetation growth can vary widely in response to heterogeneous, precipitation effects. Second, this model does not make use of eMODIS data, as we rely solely on observations collected by OLI and MSI sensors, and it outperformed Landsat-eMODIS downscaling approaches even though eMODIS data are used in the data fusion framework [17,26]. Third, this modeling framework is very flexible and can easily integrate other covariates where needed (e.g., climatic data, spectral and temporal information (e.g., Year)). Finally, disturbances (e.g., wildfires) are also captured by this modeling approach, which simpler interpolation techniques may not adequately resolve.
Future directions for the modeling component of this work include: (1) integration of other Landsat and Sentinel data (e.g., Landsat ETM+, Sentinel-2B) to better constrain models; (2) generating spatially-explicit estimates of other surface reflectance data (e.g., red-edge) and uncertainties from an ensemble of model realizations; (3) normalization of model training distributions as a function of time, to account for differences in observation density throughout the time series; and (4) assimilation of leave-one-image-out validation procedures within model calibration to independently assess model interpolation precision rather than relying on MODIS time series. We also recognize ongoing efforts by the HLS project and others to improve cloud masking algorithms for MSI data, which should be useful for expediting processing time within our overall workflow.
On average, we found that agreement between modeled and eMODIS temporal profiles of NDVI was highest for shrub/scrub and evergreen forests. Evergreen forests typically have little change in greenness from season to season and, thus, abrupt increases in NDVI within the earlier portion of the time series (Figure 5) may reflect snowmelt effects that could impact similarity metrics. Modeled estimates of NDVI were systematically lower than those of the eMODIS dataset across most land cover types, which has been previously attributed to different sensor characteristics (e.g., spatial resolution) [34,35]. The use of cross-calibrated Sentinel data as a dependent variable within our modeling framework could enhance our ability depict seasonal vegetation dynamics, particularly when a paucity of Landsat data exists. While our methodology was applied to only one year of growing season imagery, we believe that it will likely be of great value for understanding large, inter-annual variations in land-surface phenology that are commonly associated with dryland ecosystems.
Our results also hint at a systematic bias toward earlier timing of maturity and senescence of grass and shrub/scrub cover types (Figure 5 and Figure 6), which is not caused by inadequate density of observations in either time series but rather the enhanced capacity for tracking phenology using moderate resolution data than has been previously possible with coarser resolution data (e.g., MODIS). This finding agrees with those of references [18,36], where phenological transition dates (i.e., green-up, start-of-season, and maturity) extracted from Landsat time series were generally earlier than those from derived from MODIS and Visible Infrared Imaging Radiometer Suite (VIIRS) phenocurves. Others have also found a two-week lag when comparing MODIS NDVI to flux tower gross photosynthesis in rangeland ecosystems [37]. This has enormous implications for both the research community and the policy community for the management of dryland ecosystems. For example, these data allow us to detect abrupt increases in vegetation greenness associated with cheatgrass growth at fine spatial and temporal resolutions, which will allow land-use managers to take proactive steps in mitigating its impact on ecosystems and human communities.
As is demonstrated in this research, remote sensing is a cost-effective tool to describe vegetation dynamics at broad scales. Time series of vegetation indices provide the foundation from which land-surface phenology metrics (e.g., greenup, leaf-out, start of spring) are constructed [38,39]. Thus, it is vital that phenological products are derived from high quality time series data, such as those described in in this manuscript. While phenology metrics have been routinely generated from coarse-resolution data [40], data derived solely from moderate-resolution imagery (e.g., Landsat and Sentinel-2) are beginning to emerge [41]. Given the declines in MODIS performance and forthcoming decommission with no equivalent replacement planned, data fusion approaches that integrate observations from multispectral sensors (e.g., Landsat, Sentinel-2A and -2B) will be needed to effectively monitor dryland ecosystems.

6. Conclusions

In this study, we presented an innovative methodology to accurately monitor land-surface phenology in drylands of the Western United States. Our data fusion approach combined information collected by the Operational Land Imager (OLI) onboard Landsat 8 and the Multispectral Instrument (MSI) onboard Sentinel-2 using a regression tree modeling framework. This highly-automatable work flow allowed us to precisely characterize seasonal dynamics in vegetation indices with considerable agreement between spatially-explicit estimates and independent observations. We provide evidence for enhanced monitoring capabilities associated with the fusion of OLI and MSI time series, as opposed to solely using coarser resolution data or downscaling techniques that rely on a combination of Landsat and MODIS, where higher-resolution imagery allowed for early detection of plant maturity and senescence. We demonstrate that observations made by MSI and OLI can be used in amalgamation and exclusion of imagery from either sensor impairs our ability to precisely characterize vegetation dynamics in dryland environments. Other environmental applications, such as habitat and land cover mapping, will likely benefit from our time series products because they accurately capture the state of the vegetation at a spatial resolution that is meaningful to local resource managers. This research fills a critical gap in the understanding of current monitoring capabilities of arid and semi-arid environments that cover a substantial portion of the globe.

Supplementary Materials

The following are available online at https://www.mdpi.com/2072-4292/10/5/791/s1.

Author Contributions

N.J.P and B.K.W. conceived and designed the study; N.J.P. performed the analysis; and N.J.P., B.K.W., and Z.W. wrote the paper and interpreted the results.

Acknowledgments

This research was primarily supported by the United States Geological Survey’s National Land Imaging and Land Change Science Programs. N.J.P acknowledges additional funding support from the University of Minnesota’s (UMN) Doctoral Dissertation Fellowship and the Marvin E. Bauer Remote Sensing of Natural Resources Fellowship. A portion of the work was performed under USGS contract G08PC91508. Any use of trade, firm, or product names is for descriptive purposes only and does not imply endorsement by the U.S. Government.

Conflicts of Interest

The authors declare no conflict of interest.

References

  1. Huang, J.; Li, Y.; Fu, C.; Chen, F.; Fu, Q.; Dai, A.; Shinoda, M.; Ma, Z.; Guo, W.; Li, Z.; et al. Dryland climate change: Recent progress and challenges: Dryland Climate Change. Rev. Geophys. 2017, 55, 719–778. [Google Scholar] [CrossRef]
  2. Huang, J.; Yu, H.; Guan, X.; Wang, G.; Guo, R. Accelerated dryland expansion under climate change. Nat. Clim. Chang. 2016, 6, 166–171. [Google Scholar] [CrossRef]
  3. Huang, J.; Ji, M.; Xie, Y.; Wang, S.; He, Y.; Ran, J. Global semi-arid climate change over last 60 years. Clim. Dyn. 2016, 46, 1131–1150. [Google Scholar] [CrossRef]
  4. Poulter, B.; Frank, D.; Ciais, P.; Myneni, R.B.; Andela, N.; Bi, J.; Broquet, G.; Canadell, J.G.; Chevallier, F.; Liu, Y.Y.; et al. Contribution of semi-arid ecosystems to interannual variability of the global carbon cycle. Nature 2014, 509, 600–603. [Google Scholar] [CrossRef] [PubMed]
  5. Brooks, M.L.; D’Antonio, C.M.; Richardson, D.M.; Grace, J.B.; Keeley, J.E.; DiTomaso, J.M.; Hobbs, R.J.; Pellant, M.; Pyke, D. Effects of Invasive Alien Plants on Fire Regimes. BioScience 2004, 54, 677–688. [Google Scholar] [CrossRef]
  6. Wang, L.; D’Odorico, P.; Evans, J.P.; Eldridge, D.J.; McCabe, M.F.; Caylor, K.K.; King, E.G. Dryland ecohydrology and climate change: Critical issues and technical advances. Hydrol. Earth Syst. Sci. 2012, 16, 2585–2603. [Google Scholar] [CrossRef] [Green Version]
  7. Zhang, Y.; Song, C.; Band, L.E.; Sun, G.; Li, J. Reanalysis of global terrestrial vegetation trends from MODIS products: Browning or greening? Remote Sens. Environ. 2017, 191, 145–155. [Google Scholar] [CrossRef]
  8. Zhang, Y.; Xiao, X.; Wu, X.; Zhou, S.; Zhang, G.; Qin, Y.; Dong, J. A global moderate resolution dataset of gross primary production of vegetation for 2000–2016. Sci. Data 2017, 4, 170165. [Google Scholar] [CrossRef] [PubMed]
  9. Zhu, Z.; Bi, J.; Pan, Y.; Ganguly, S.; Anav, A.; Xu, L.; Samanta, A.; Piao, S.; Nemani, R.; Myneni, R. Global Data Sets of Vegetation Leaf Area Index (LAI)3g and Fraction of Photosynthetically Active Radiation (FPAR)3g Derived from Global Inventory Modeling and Mapping Studies (GIMMS) Normalized Difference Vegetation Index (NDVI3g) for the Period 1981 to 2011. Remote Sens. 2013, 5, 927–948. [Google Scholar] [CrossRef]
  10. Hansen, M.C.; Potapov, P.V.; Moore, R.; Hancher, M.; Turubanova, S.A.; Tyukavina, A.; Thau, D.; Stehman, S.V.; Goetz, S.J.; Loveland, T.R.; et al. High-Resolution Global Maps of 21st-Century Forest Cover Change. Science 2013, 342, 850–853. [Google Scholar] [CrossRef] [PubMed]
  11. Pekel, J.-F.; Cottam, A.; Gorelick, N.; Belward, A.S. High-resolution mapping of global surface water and its long-term changes. Nature 2016, 540, 418–422. [Google Scholar] [CrossRef] [PubMed]
  12. Wulder, M.A.; Coops, N.C. Make Earth Observations Open Access. Nature 2014, 513, 30–31. [Google Scholar] [CrossRef] [PubMed]
  13. Wulder, M.A.; Masek, J.G.; Cohen, W.B.; Loveland, T.R.; Woodcock, C.E. Opening the archive: How free data has enabled the science and monitoring promise of Landsat. Remote Sens. Environ. 2012, 122, 2–10. [Google Scholar] [CrossRef]
  14. Zhu, Z.; Woodcock, C.E.; Holden, C.; Yang, Z. Generating synthetic Landsat images based on all available Landsat data: Predicting Landsat surface reflectance at any given time. Remote Sens. Environ. 2015, 162, 67–83. [Google Scholar] [CrossRef]
  15. Olsoy, P.; Mitchell, J.; Glenn, N.; Flores, A. Assessing a Multi-Platform Data Fusion Technique in Capturing Spatiotemporal Dynamics of Heterogeneous Dryland Ecosystems in Topographically Complex Terrain. Remote Sens. 2017, 9, 981. [Google Scholar] [CrossRef]
  16. Liao, L.; Song, J.; Wang, J.; Xiao, Z.; Wang, J. Bayesian Method for Building Frequent Landsat-Like NDVI Datasets by Integrating MODIS and Landsat NDVI. Remote Sens. 2016, 8, 452. [Google Scholar] [CrossRef]
  17. Gu, Y.; Wylie, B. Downscaling 250-m MODIS Growing Season NDVI Based on Multiple-Date Landsat Images and Data Mining Approaches. Remote Sens. 2015, 7, 3489–3506. [Google Scholar] [CrossRef]
  18. Baumann, M.; Ozdogan, M.; Richardson, A.D.; Radeloff, V.C. Phenology from Landsat when data is scarce: Using MODIS and Dynamic Time-Warping to combine multi-year Landsat imagery to derive annual phenology curves. Int. J. Appl. Earth Obs. Geoinf. 2017, 54, 72–83. [Google Scholar] [CrossRef]
  19. Wang, Q.; Blackburn, G.A.; Onojeghuo, A.O.; Dash, J.; Zhou, L.; Zhang, Y.; M, P. Atkinson Fusion of Landsat 8 OLI and Sentinel-2 MSI Data. IEEE Trans. Geosci. Remote Sens. 2017, 55, 3885–3899. [Google Scholar] [CrossRef]
  20. Li, J.; Roy, D. A Global Analysis of Sentinel-2A, Sentinel-2B and Landsat-8 Data Revisit Intervals and Implications for Terrestrial Monitoring. Remote Sens. 2017, 9, 902. [Google Scholar] [CrossRef]
  21. Homer, C.; Dewitz, J.; Yang, L.; Jin, S.; Danielson, P.; Xian, G.; Coulston, J.; Herold, N.; Wickham, J.; Megown, K. Completion of the 2011 National Land Cover Database for the Conterminous United States—Representing a Decade of Land Cover Change Information. Photogramm. Eng. Remote Sens. 2015, 81, 345–354. [Google Scholar] [CrossRef]
  22. Boyte, S.P.; Wylie, B.K.; Major, D.J. Cheatgrass percent cover change: Comparing recent estimates to climate change—Driven predictions in the Northern Great Basin. Rangel. Ecol. Manag. 2016, 69, 265–279. [Google Scholar] [CrossRef]
  23. Claverie, M.; Masek, J.G.; Ju, J.; Dungan, J.L. Harmonized Landsat-8 Sentinel-2 (HLS) Product User’s Guide; National Aeronautics and Space Administration (NASA): Washington, DC, USA, 2017.
  24. Jenkerson, C.B.; Maiersperger, T.K.; Schmidt, G.L. eMODIS: A User-Friendly Data Source; Open-File Report 2010-1055; U.S. Geological Survey: Reston, VA, USA, 2010.
  25. Swets, D.L.; Reed, B.C.; Rowland, J.R.; Marko, S.E. A weighted least-squares approach to temporal smoothing of NDVI. In Proceedings of the ASPRS Annual Conference, Portland, OR, USA, 17–21 May 1999. [Google Scholar]
  26. Boyte, S.P.; Wylie, B.K.; Rigge, M.B.; Dahal, D. Fusing MODIS with Landsat 8 data to downscale weekly normalized difference vegetation index estimates for central Great Basin rangelands, USA. GISci. Remote Sens. 2018, 55, 376–399. [Google Scholar] [CrossRef]
  27. Zhu, Z.; Woodcock, C.E. Object-based cloud and cloud shadow detection in Landsat imagery. Remote Sens. Environ. 2012, 118, 83–94. [Google Scholar] [CrossRef]
  28. Vermote, E.; Justice, C.; Claverie, M.; Franch, B. Preliminary analysis of the performance of the Landsat 8/OLI land surface reflectance product. Remote Sens. Environ. 2016, 185, 46–56. [Google Scholar] [CrossRef]
  29. Foga, S.; Scaramuzza, P.L.; Guo, S.; Zhu, Z.; Dilley, R.D.; Beckmann, T.; Schmidt, G.L.; Dwyer, J.L.; Joseph Hughes, M.; Laue, B. Cloud detection algorithm comparison and validation for operational Landsat data products. Remote Sens. Environ. 2017, 194, 379–390. [Google Scholar] [CrossRef]
  30. Li, S.; Ganguly, S.; Dungan, J.L.; Wang, W.; Nemani, R.R. Sentinel-2 MSI Radiometric Characterization and Cross-Calibration with Landsat-8 OLI. Adv. Remote Sens. 2017, 6, 147–159. [Google Scholar] [CrossRef]
  31. Quinlan, J.R. C4.5: Programs for Machine Learning; Morgan Kaufmann Publishers Inc.: San Francisco, CA, USA, 1993; ISBN 1-55860-238-0. [Google Scholar]
  32. Chen, H.; Yao, X. Ensemble regression trees for time series predictions. Neurocomputing 2007, 70, 697–703. [Google Scholar] [CrossRef]
  33. Elmore, A.J.; Guinn, S.M.; Minsley, B.J.; Richardson, A.D. Landscape controls on the timing of spring, autumn, and growing season length in mid-Atlantic forests. Glob. Chang. Biol. 2012, 18, 656–674. [Google Scholar] [CrossRef]
  34. Singh, D. Generation and evaluation of gross primary productivity using Landsat data through blending with MODIS data. Int. J. Appl. Earth Obs. 2011, 13, 59–69. [Google Scholar] [CrossRef]
  35. Hwang, T.; Kang, S.; Kim, J.; Kim, Y.; Lee, D.; Band, L. Evaluating drought effect on MODIS Gross Primary Production (GPP) with an eco-hydrological model in the mountainous forest, East Asia. Glob. Chang. Biol. 2008, 14, 1037–1056. [Google Scholar] [CrossRef]
  36. Zhang, X.; Wang, J.; Gao, F.; Liu, Y.; Schaaf, C.; Friedl, M.; Yu, Y.; Jayavelu, S.; Gray, J.; Liu, L.; et al. Exploration of scaling effects on coarse resolution land surface phenology. Remote Sens. Environ. 2017, 190, 318–330. [Google Scholar] [CrossRef]
  37. Rigge, M.; Smart, A.; Wylie, B.; Gilmanov, T.; Johnson, P. Linking Phenology and Biomass Productivity in South Dakota Mixed-Grass Prairie. Rangel. Ecol. Manag. 2013, 66, 579–587. [Google Scholar] [CrossRef]
  38. White, M.A.; de Beurs, K.M.; Didan, K.; Inouye, D.W.; Richardson, A.D.; Jensen, O.P.; O’Keefe, J.; Zhang, G.; Nemani, R.R.; van Leeuwen, W.J.D.; et al. Intercomparison, interpretation, and assessment of spring phenology in North America estimated from remote sensing for 1982–2006. Glob. Chang. Biol. 2009, 15, 2335–2359. [Google Scholar] [CrossRef]
  39. Peng, D.; Wu, C.; Zhang, X.; Yu, L.; Huete, A.R.; Wang, F.; Luo, S.; Liu, X.; Zhang, H. Scaling up spring phenology derived from remote sensing images. Agric. For. Meteorol. 2018, 256–257, 207–219. [Google Scholar] [CrossRef]
  40. Zhang, X.; Liu, L.; Yan, D. Comparisons of global land surface seasonality and phenology derived from AVHRR, MODIS, and VIIRS data. J. Geophys. Res. Biogeosci. 2017, 122, 1506–1525. [Google Scholar] [CrossRef]
  41. Jönsson, P.; Cai, Z.; Melaas, E.; Friedl, M.A.; Eklundh, L. A Method for Robust Estimation of Vegetation Seasonality from Landsat and Sentinel-2 Time Series Data. Remote Sens. 2018, 10. [Google Scholar] [CrossRef]
Remotesensing 10 00791 g001 550
Figure 1. Land cover information from the National Land Cover Database 2011 (NLCD; [21]) overlain by our study area (i.e., Harmonized Landsat-8 Sentinel-2 tile (11SQD)).
Figure 1. Land cover information from the National Land Cover Database 2011 (NLCD; [21]) overlain by our study area (i.e., Harmonized Landsat-8 Sentinel-2 tile (11SQD)).
Remotesensing 10 00791 g001
Remotesensing 10 00791 g002 550
Figure 2. Schematic diagram of overall workflow.
Figure 2. Schematic diagram of overall workflow.
Remotesensing 10 00791 g002
Remotesensing 10 00791 g003 550
Figure 3. (Left) Harmonized Landsat-8 Sentinel-2 (HLS) imagery (RGB; Bands 4, 3, and 2) overlaid by mask layers created using LaSRC (Top Middle [28]), FMask (Bottom Middle [27]); and (Right) decision tree models.
Figure 3. (Left) Harmonized Landsat-8 Sentinel-2 (HLS) imagery (RGB; Bands 4, 3, and 2) overlaid by mask layers created using LaSRC (Top Middle [28]), FMask (Bottom Middle [27]); and (Right) decision tree models.
Remotesensing 10 00791 g003
Remotesensing 10 00791 g004 550
Figure 4. Comparison of surface reflectance data from Harmonized Landsat-Sentinel-2 (HLS) products for one-day-apart acquisitions. Darker regions represent larger numbers of points (n = 50,000). Dashed-green line is 1-to-1 and the red line is the ordinary least squares (OLS) regression fit showing proportional bias.
Figure 4. Comparison of surface reflectance data from Harmonized Landsat-Sentinel-2 (HLS) products for one-day-apart acquisitions. Darker regions represent larger numbers of points (n = 50,000). Dashed-green line is 1-to-1 and the red line is the ordinary least squares (OLS) regression fit showing proportional bias.
Remotesensing 10 00791 g004
Remotesensing 10 00791 g005 550
Figure 5. Time series of Harmonized Landsat-8 Sentinel-2 (HLS), predicted, and eMODIS Normalized Difference Vegetation Index (NDVI × 100) separated by major land cover classes [21]. ModelLS was generated using both Landsat-8 and Sentinel-2A inputs, while ModelL was generated using only Landsat-8 inputs. Each time series is calculated from all pixels (excluding masked pixels in the original HLS time series) representing largely homogenous areas (coefficient of variation < 40%) and smoothed using a three-week sliding window approach. Timesteps where HLS data coverage was less than 70% are not shown.
Figure 5. Time series of Harmonized Landsat-8 Sentinel-2 (HLS), predicted, and eMODIS Normalized Difference Vegetation Index (NDVI × 100) separated by major land cover classes [21]. ModelLS was generated using both Landsat-8 and Sentinel-2A inputs, while ModelL was generated using only Landsat-8 inputs. Each time series is calculated from all pixels (excluding masked pixels in the original HLS time series) representing largely homogenous areas (coefficient of variation < 40%) and smoothed using a three-week sliding window approach. Timesteps where HLS data coverage was less than 70% are not shown.
Remotesensing 10 00791 g005
Remotesensing 10 00791 g006 550
Figure 6. Time series of Harmonized Landsat-8 Sentinel-2 (HLS), predicted, and eMODIS Normalized Difference Vegetation Index (NDVI × 100) separated by percentage cheatgrass cover [22]. ModelLS was generated using both Landsat-8 and Sentinel-2A inputs, while ModelL was generated using only Landsat-8 inputs. Each time series was from all pixels (excluding masked areas in the original HLS time series) and smoothed using a three-week sliding window approach. Timesteps where HLS data coverage was less than 70% are not shown.
Figure 6. Time series of Harmonized Landsat-8 Sentinel-2 (HLS), predicted, and eMODIS Normalized Difference Vegetation Index (NDVI × 100) separated by percentage cheatgrass cover [22]. ModelLS was generated using both Landsat-8 and Sentinel-2A inputs, while ModelL was generated using only Landsat-8 inputs. Each time series was from all pixels (excluding masked areas in the original HLS time series) and smoothed using a three-week sliding window approach. Timesteps where HLS data coverage was less than 70% are not shown.
Remotesensing 10 00791 g006
Remotesensing 10 00791 g007 550
Figure 7. eMODIS versus predicted (upscaled to 250-m spatial resolution using bilinear interpolation) growing season (April–September) Normalized Difference Vegetation Index (NDVI × 100) for randomly selected pixels (n ~ 10,000). ModelLS was generated using both harmonized Landsat-8 and Sentinel-2A inputs, while ModelL was generated using only harmonized Landsat-8 inputs. Darker regions represent larger numbers of sampled pixels. Dashed-green line is 1-to-1 and the red line is the ordinary-least squares regression fit weighted by the inverse of the coefficient of variation (CV) determined from a focal scan of the eMODIS Growing Season NDVI product (e.g., more weight to homogenous areas [larger points]).
Figure 7. eMODIS versus predicted (upscaled to 250-m spatial resolution using bilinear interpolation) growing season (April–September) Normalized Difference Vegetation Index (NDVI × 100) for randomly selected pixels (n ~ 10,000). ModelLS was generated using both harmonized Landsat-8 and Sentinel-2A inputs, while ModelL was generated using only harmonized Landsat-8 inputs. Darker regions represent larger numbers of sampled pixels. Dashed-green line is 1-to-1 and the red line is the ordinary-least squares regression fit weighted by the inverse of the coefficient of variation (CV) determined from a focal scan of the eMODIS Growing Season NDVI product (e.g., more weight to homogenous areas [larger points]).
Remotesensing 10 00791 g007
Remotesensing 10 00791 g008 550
Figure 8. eMODIS versus predicted (upscaled to 250-m spatial resolution using bilinear interpolation) normalized difference vegetation index (NDVI × 100) for randomly selected pixels (n ~ 10,000) during Weeks 22 and 23. ModelLS was generated using both harmonized Landsat-8 and Sentinel-2A inputs, while downscaled NDVI was generated using regression tree models with harmonized Landsat-8 and eMODIS inputs. Darker regions represent larger numbers of sampled points. Dashed-green line is 1-to-1 and the red line is the ordinary-least squares regression fit weighted by the inverse of the coefficient of variation (CV) determined from a focal scan of the eMODIS growing season NDVI product (e.g., more weight to homogenous areas [larger points]).
Figure 8. eMODIS versus predicted (upscaled to 250-m spatial resolution using bilinear interpolation) normalized difference vegetation index (NDVI × 100) for randomly selected pixels (n ~ 10,000) during Weeks 22 and 23. ModelLS was generated using both harmonized Landsat-8 and Sentinel-2A inputs, while downscaled NDVI was generated using regression tree models with harmonized Landsat-8 and eMODIS inputs. Darker regions represent larger numbers of sampled points. Dashed-green line is 1-to-1 and the red line is the ordinary-least squares regression fit weighted by the inverse of the coefficient of variation (CV) determined from a focal scan of the eMODIS growing season NDVI product (e.g., more weight to homogenous areas [larger points]).
Remotesensing 10 00791 g008
Table
Table 1. Harmonized Landsat-8 OLI and Sentinel-2 MSI images (n = 30) acquired in 2016 and used within the study.
Table 1. Harmonized Landsat-8 OLI and Sentinel-2 MSI images (n = 30) acquired in 2016 and used within the study.
Product NameSensorDay of YearAcquisition TimeQuality (%) ††Cloud + Shadow (%)
HLS.L30.T11SQD.2016064.v1.3.hdfLandsat OLI6418:14:270.820.18
HLS.S30.T11SQD.2016077.v1.3.hdfSentinel-2A7718:30:210.710.22
HLS.L30.T11SQD.2016080.v1.3.hdfLandsat OLI8018:14:210.80.24
HLS.L30.T11SQD.2016096.v1.3.hdf †Landsat OLI9618:14:130.820.2
HLS.S30.T11SQD.2016097.v1.3.hdf †Sentinel-2A9718:33:060.930
HLS.S30.T11SQD.2016107.v1.3.hdfSentinel-2A10718:24:110.710.27
HLS.L30.T11SQD.2016112.v1.3.hdfLandsat OLI11218:14:060.80.22
HLS.L30.T11SQD.2016128.v1.3.hdfLandsat OLI12818:14:090.470.80
HLS.L30.T11SQD.2016144.v1.3.hdfLandsat OLI14418:14:110.70.48
HLS.S30.T11SQD.2016157.v1.3.hdfSentinel-2A15718:27:420.990
HLS.L30.T11SQD.2016160.v1.3.hdfLandsat OLI16018:14:150.80.31
HLS.L30.T11SQD.2016176.v1.3.hdf †Landsat OLI17618:14:210.980.02
HLS.S30.T11SQD.2016177.v1.3.hdf †Sentinel-2A17718:22:310.990
HLS.S30.T11SQD.2016187.v1.3.hdfSentinel-2A18718:33:120.980.02
HLS.L30.T11SQD.2016192.v1.3.hdfLandsat OLI19218:14:300.950.07
HLS.S30.T11SQD.2016197.v1.3.hdfSentinel-2A19718:30:130.890.1
HLS.S30.T11SQD.2016207.v1.3.hdf †Sentinel-2A20718:33:130.980.01
HLS.L30.T11SQD.2016208.v1.3.hdf †Landsat OLI20818:14:340.970.03
HLS.S30.T11SQD.2016217.v1.3.hdfSentinel-2A21718:21:550.750.25
HLS.L30.T11SQD.2016224.v1.3.hdfLandsat OLI22418:14:360.980.02
HLS.S30.T11SQD.2016227.v1.3.hdfSentinel-2A22718:33:120.940.06
HLS.S30.T11SQD.2016237.v1.3.hdfSentinel-2A23718:21:500.960.04
HLS.L30.T11SQD.2016240.v1.3.hdfLandsat OLI24018:14:440.930.11
HLS.S30.T11SQD.2016247.v1.3.hdfSentinel-2A24718:33:090.930.07
HLS.L30.T11SQD.2016256.v1.3.hdf †Landsat OLI25618:14:480.820.27
HLS.S30.T11SQD.2016257.v1.3.hdf †Sentinel-2A25718:22:130.830.17
HLS.L30.T11SQD.2016272.v1.3.hdfLandsat OLI27218:14:480.760.38
HLS.S30.T11SQD.2016307.v1.3.hdfSentinel-2A30718:33:070.910.08
HLS.L30.T11SQD.2016320.v1.3.hdfLandsat OLI32018:14:540.920.08
HLS.S30.T11SQD.2016327.v1.3.hdfSentinel-2A32718:28:020.780.17
† Imagery used in one-day-apart comparisons; †† Refers to percentage of pixels where quality assessment band equals zero.
Table
Table 2. Confusion matrices constructed from random hold-out samples of observed versus mapped values for binary (i.e., cloud, shadow, snow/ice, water (yes), or clear (no)) decision tree masking models developed for (top) Landsat-8 OLI and (bottom) Sentinel-2 MSI data throughout the study period.
Table 2. Confusion matrices constructed from random hold-out samples of observed versus mapped values for binary (i.e., cloud, shadow, snow/ice, water (yes), or clear (no)) decision tree masking models developed for (top) Landsat-8 OLI and (bottom) Sentinel-2 MSI data throughout the study period.
ReferenceRow TotalUser’s Accuracy
NoYes
MapNo182,582264182,84699.9
Yes18426,68426,86899.3
Column Total182,76626,948--
Producer’s Accuracy99.999--
Overall Accuracy---99.8
 
ReferenceRow TotalUser’s Accuracy
NoYes
MapNo292,913879293,79299.7
Yes36447,33547,69999.2
Column Total293,27748,214--
Producer’s Accuracy99.998.2--
Overall Accuracy---99.6
Table
Table 3. Statistical metrics derived from observed and predicted (ModelLS) normalized difference vegetation index (NDVI × 100) values for a random hold-out sample.
Table 3. Statistical metrics derived from observed and predicted (ModelLS) normalized difference vegetation index (NDVI × 100) values for a random hold-out sample.
Day of Year064080096112128144160176192208224240256272320All
R20.920.970.980.960.960.960.980.990.980.990.990.990.980.960.980.98
MAE1.410.750.940.971.681.371.140.921.090.860.870.871.121.541.371.09
rMAE0.080.080.040.040.070.050.040.030.040.030.030.030.040.060.060.04
RMSE2.801.351.741.842.162.662.121.642.081.531.711.532.303.012.252.09
n732961658172606661656503928010,89410,73210,75810,9429964861972749321125,453
MAE = Mean Absolute Error; rMAE = relative Mean Absolute Error; RMSE = Root-mean Squared Error.

Share and Cite

MDPI and ACS Style

Pastick, N.J.; Wylie, B.K.; Wu, Z. Spatiotemporal Analysis of Landsat-8 and Sentinel-2 Data to Support Monitoring of Dryland Ecosystems. Remote Sens. 2018, 10, 791. https://doi.org/10.3390/rs10050791

AMA Style

Pastick NJ, Wylie BK, Wu Z. Spatiotemporal Analysis of Landsat-8 and Sentinel-2 Data to Support Monitoring of Dryland Ecosystems. Remote Sensing. 2018; 10(5):791. https://doi.org/10.3390/rs10050791

Chicago/Turabian Style

Pastick, Neal J., Bruce K. Wylie, and Zhuoting Wu. 2018. "Spatiotemporal Analysis of Landsat-8 and Sentinel-2 Data to Support Monitoring of Dryland Ecosystems" Remote Sensing 10, no. 5: 791. https://doi.org/10.3390/rs10050791

APA Style

Pastick, N. J., Wylie, B. K., & Wu, Z. (2018). Spatiotemporal Analysis of Landsat-8 and Sentinel-2 Data to Support Monitoring of Dryland Ecosystems. Remote Sensing, 10(5), 791. https://doi.org/10.3390/rs10050791

Note that from the first issue of 2016, this journal uses article numbers instead of page numbers. See further details here.

Article Metrics

Back to TopTop