Hierarchical Fusion of Convolutional Neural Networks and Attributed Scattering Centers with Application to Robust SAR ATR
Abstract
:1. Introduction
2. CNN
2.1. Basic Theory
2.2. Architecture of the Proposed CNN
3. ASC Matching
3.1. ASC Model
3.2. Sparse Representation for ASC Extraction
| Algorithm 1 OMP for ASC Extraction |
| Input: The measurements , estimated noise level , and redundant parameterized dictionary . Initialization: The initial parameter set of the ASCs , reconstruction residual , and iteration counter . 1. while do 2. Calculate correlation: , where denotes conjugate transpose. 3. Estimate parameters: , . 4. Estimate amplitudes: , where denotes the Moore-Penrose pseudo-inverse, represents the dictionary constructed by the parameter set . 5. Update residual: . 6. Output: The estimated parameters set . |
3.3. ASC Matching
3.3.1. One-To-One Matching between ASC Sets
- (1)
- Distance measure for two individual ASCs
- (2)
- ASC matching using the Hungarian algorithm
3.3.2. Similarity Evaluation
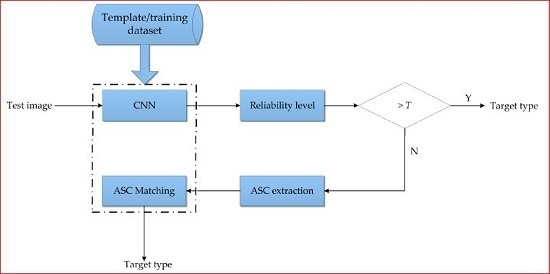
4. Hierarchical Fusion of CNN and ASC Matching for SAR ATR
5. Experiment
5.1. Data Preparation and Experimental Setup
5.2. Recognition under SOC
5.2.1. Preliminary Verification
5.2.2. Performance under Different Thresholds
5.3. Recognition under EOCs
5.3.1. Configuration Variance
5.3.2. Large Depression Angle Variance
5.3.3. Noise Corruption
5.3.4. Partial Occlusion
5.4. Limited Training Samples
6. Discussion
- (i)
- Experiment under SOC. Under SOC, the training and test samples are notably similar with only a 2° depression angle difference. Consequently, all the methods achieve very high PCCs. Due to the powerful classification capability of CNN under SOC, most test samples are actually classified by CNN in the proposed method. The remaining ones can also be effectively classified by ASC matching because of its goof performance. Hence, the hierarchical fusion of the two classification schemes can maintain the excellent performance under SOC, which is demonstrated to outperform the others. In this case, the excellent performance of the proposed method mainly benefits from CNN. Meanwhile, ASC matching further improves the recognition performance by handling a few test samples, which possibly have many differences with the training ones.
- (ii)
- Experiment under EOCs. The EOCs like configuration variance, depression angle variance, noise corruption and partial occlusion probably cause some local variations of the target in the test SAR images. Therefore, the one-to-one correspondence between the local descriptors, i.e., ASCs, can better handle these situations. For the classifiers like SVM, SRC and CNN, the training samples only include SAR images of intact targets with high SNRs. In addition, only a specific configuration is bracketed. Therefore, their performances degrade greatly under these EOCs. In the proposed method, when a test sample cannot be reliably classified by CNN, ASC matching can probably provide a correct decision. Therefore, via hierarchically fusing CNN and ASC matching, the robustness of the proposed method can be enhanced. In this case, the superior robustness of the proposed method mainly benefits from the merits of ASC matching. However, for those EOCs which are not severely different from the training set (e.g., small amount of noise additions), CNN is probable to make correct decisions on them. Therefore, CNN can complement ASC matching to further improve ATR performance.
- (iii)
- Experiment under limited training samples. With limited training samples, the classification capabilities of SVM, SRC and CNN will be impaired greatly. For the ASC matching method, the template ASCs still share a high correlation with the test ASCs because the stability of ASCs can be maintained in a certain azimuth interval. Therefore, once the CNN cannot form a reliable decision for the test image, the ASC matching can better cope with the situation.
7. Conclusions
- (i)
- CNN has powerful classification capability under SOC. Thus, it is a reasonable choice to use is as the basic classifier. In addition, ASC matching can also work very well under SOC because of the good discrimination of ASCs. Therefore, the hierarchical fusion of the two classification schemes can maintain excellent performance under SOC.
- (ii)
- ASC matching can achieve very good robustness under different types of EOCs. The one-to-one correspondence between two ASC sets can sense the local variations of the target thus the resulted similarity measure can better handle these situations. Therefore, those samples which cannot be reliably classified by CNN are probably to obtain correct decisions by ASC matching.
- (iii)
- The proposed method achieves the best performance under both SOC and EOCs compared with other state-of-the-art methods by combining the merits of the two classification schemes.
Author Contributions
Acknowledgments
Conflicts of Interest
References
- Xu, Z.; Chen, K.S. On signal modeling of moon-based synthetic aperture radar (SAR) imaging of earth. Remote Sens. 2018, 10, 486. [Google Scholar] [CrossRef]
- Ao, D.Y.; Wang, R.; Hu, C.; Li, Y.H. A sparse SAR imaging method based on multiple measurement vectors model. Remote Sens. 2017, 9, 297. [Google Scholar] [CrossRef]
- Cumming, I.G.; Wong, F.H. Digital Processing of Synthetic Aperture radar Data: Algorithms and Implementation; Artech House: London, UK, 2004; ISBN 978-7-121-16977-9. [Google Scholar]
- Argenti, F.; Lapini, A.; Bianchi, T.; Alparone, L. A tutorial on speckle reduction in synthetic aperture radar Images. IEEE Geosci. Remote Sens. Mag. 2013, 1, 6–35. [Google Scholar] [CrossRef]
- El-Darymli, K.; Gill, E.W.; McGuire, P.; Power, D.; Moloney, C. Automatic target recognition in synthetic aperture radar imagery: A state-of-the-art review. IEEE Access 2016, 4, 6014–6058. [Google Scholar] [CrossRef]
- El-Darymli, K.; McGuire, P.; Power, D.; Moloney, C. Target detection in synthetic aperture radar imagery: A state-of-the-art survey. J. Appl. Remote Sens. 2013, 13, 071598. [Google Scholar] [CrossRef]
- Gao, G. An improved scheme for target discrimination in high-resolution SAR images. IEEE Trans. Geosci. Remote Sens. 2011, 49, 277–294. [Google Scholar] [CrossRef]
- Ding, B.Y.; Wen, G.J.; Ma, C.H.; Yang, X.L. Target recognition in synthetic aperture radar images using binary morphological operations. J. Appl. Remote Sens. 2016, 10, 046006. [Google Scholar] [CrossRef]
- Amoon, M.; Rezai-rad, G. Automatic target recognition of synthetic aperture radar (SAR) images based on optimal selection of Zernike moment features. IET Comput. Vis. 2014, 8, 77–85. [Google Scholar] [CrossRef]
- Park, J.; Park, S.; Kim, K. New discrimination features for SAR automatic target recognition. IEEE Geosci. Remote Sens. Lett. 2013, 10, 476–480. [Google Scholar] [CrossRef]
- Anagnostopulos, G.C. SVM-based target recognition from synthetic aperture radar images using target region outline descriptors. Nonlinear Anal. 2009, 71, e2934–e2939. [Google Scholar] [CrossRef]
- Papson, S.; Narayanan, R.M. Classification via the shadow region in SAR imagery. IEEE Trans. Aerosp. Electron. Syst. 2012, 48, 969–980. [Google Scholar] [CrossRef]
- Cui, J.J.; Gudnason, J.; Brookes, M. Automatic recognition of MSTAR targets using radar shadow and super resolution features for. In Proceedings of the IEEE International Conference on Acoustics, Speech, and Signal Processing (ICASSP), Philadelphia, PA, USA, 18–23 March 2005. [Google Scholar]
- Mishra, A.K. Validation of PCA and LDA for SAR ATR. In Proceedings of the 2008 IEEE Region 10 Conference, Hyderabad, India, 19–21 November 2008; pp. 1–6. [Google Scholar]
- Cui, Z.Y.; Cao, Z.J.; Yang, J.Y.; Feng, J.L.; Ren, H.L. Target recognition in synthetic aperture radar via non-negative matrix factorization. IET Radar Sonar Navig. 2015, 9, 1376–1385. [Google Scholar] [CrossRef]
- Huang, Y.L.; Pei, J.F.; Yang, J.Y.; Liu, X. Neighborhood geometric center scaling embedding for SAR ATR. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 180–192. [Google Scholar] [CrossRef]
- Yu, M.T.; Dong, G.G.; Fan, H.Y.; Kuang, G.Y. SAR target recognition via local sparse representation of multi-manifold regularized low-rank approximation. Remote Sens. 2018, 10, 211. [Google Scholar]
- Gerry, M.J.; Potter, L.C.; Gupta, I.J.; Merwe, A. A parametric model for synthetic aperture radar measurement. IEEE Trans. Antennas Propag. 1999, 47, 1179–1188. [Google Scholar] [CrossRef]
- Potter, L.C.; Mose, R.L. Attributed scattering centers for SAR ATR. IEEE Trans. Image Process. 1997, 6, 79–91. [Google Scholar] [CrossRef] [PubMed]
- Bhanu, B.; Lin, Y. Stochastic models for recognition of occluded targets. Pattern Recognit. 2003, 36, 2855–2873. [Google Scholar] [CrossRef]
- Chiang, H.; Moses, R.L.; Potter, L.C. Model-based classification of radar images. IEEE Trans. Inf. Theory 2000, 46, 1842–1854. [Google Scholar] [CrossRef]
- Ding, B.Y.; Wen, G.J.; Huang, X.H.; Ma, C.H.; Yang, X.L. Target recognition in synthetic aperture radar images via matching of attributed scattering centers. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 3334–3347. [Google Scholar] [CrossRef]
- Ding, B.Y.; Wen, G.J.; Zhong, J.R.; Ma, C.H.; Yang, X.L. A robust similarity measure for attributed scattering center sets with application to SAR ATR. Neurocomputing 2017, 219, 130–143. [Google Scholar] [CrossRef]
- Ding, B.Y.; Wen, G.J.; Zhong, J.R.; Ma, C.H.; Yang, X.L. Robust method for the matching of attributed scattering centers with application to synthetic aperture radar automatic target recognition. J. Appl. Remote Sens. 2016, 10, 016010. [Google Scholar] [CrossRef]
- Ding, B.Y.; Wen, G.J.; Huang, X.H.; Ma, C.H.; Yang, X.L. Data augmentation by multilevel reconstruction using attributed scattering center for SAR target recognition. IEEE Geosci. Remote Sens. Lett. 2017, 14, 979–983. [Google Scholar] [CrossRef]
- Zhou, J.X.; Shi, Z.G.; Cheng, X.; Fu, Q. Automatic target recognition of SAR images based on global scattering center model. IEEE Trans. Geosci. Remote Sens. 2011, 49, 3713–3729. [Google Scholar]
- Ding, B.Y.; Wen, G.J. A region matching approach based on 3-D scattering center model with application to SAR target recognition. IEEE Sens. J. 2018, 18, 4623–4632. [Google Scholar] [CrossRef]
- Sun, Y.J.; Liu, Z.P.; Todorovic, S.; Li, J. Adaptive boosting for SAR automatic target recognition. IEEE Trans. Aerosp. Electron. Syst. 2007, 43, 112–125. [Google Scholar] [CrossRef]
- Srinivas, U.; Monga, V.; Raj, R.G. SAR automatic target recognition using discriminative graphical models. IEEE Trans. Aerosp. Electron. Syst. 2014, 50, 591–606. [Google Scholar] [CrossRef]
- Zhao, Q.; Principe, J.C. Support vector machines for synthetic radar automatic target recognition. IEEE Trans. Aerosp. Electron. Syst. 2001, 37, 643–654. [Google Scholar] [CrossRef]
- Liu, H.C.; Li, S.T. Decision fusion of sparse representation and support vector machine for SAR image target recognition. Neurocomputing 2013, 113, 97–104. [Google Scholar] [CrossRef]
- Song, H.B.; Ji, K.F.; Zhang, Y.S.; Xing, X.W.; Zou, H.X. Sparse representation-based SAR image target classification on the 10-class MSTAR data set. Appl. Sci. 2016, 6, 26. [Google Scholar] [CrossRef]
- Thiagarajan, J.; Ramamurthy, K.; Knee, P.P.; Spanias, A.; Berisha, V. Sparse representation for automatic target classification in SAR images. In Proceedings of the 2010 4th Communications, Control and Signal Processing (ISCCSP), Limassol, Cyprus, 3–5 March 2010. [Google Scholar]
- Krizhevsky, A.; Sutskever, I.; Hinton, G.E. Imagenet classification with deep convolutional neural networks. In Proceedings of the Neural Information Processing System (NIPS), Harrahs and Harveys, Lake Tahoe, NV, USA, 3–8 December 2012; Volume 2, pp. 1096–1105. [Google Scholar]
- Szegedu, C.; Liu, W.; Jia, Y.; Sermanet, P.; Reed, S.; Anguelov, D.L.; Erhan, D.; Vanhoucke, V.; Rabinovich, A. Going deeper with convolutions. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Boston, MA, USA, 7–12 June 2015; pp. 1–9. [Google Scholar]
- He, K.; Zhang, X.; Ren, S.; Sun, J. Deep residual learning for image recognition. In Proceedings of the IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, NV, USA, 17–30 June 2016; pp. 770–778. [Google Scholar]
- Dong, G.G.; Kuang, G.Y.; Wang, N.; Zhao, L.J.; Lu, J. SAR target recognition via joint sparse representation of monogenic signal. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2015, 8, 3316–3328. [Google Scholar] [CrossRef]
- Ding, B.Y.; Wen, G.J. Sparsity constraint nearest subspace classifier for target recognition of SAR images. J. Vis. Commun. Image Represent. 2018, 52, 170–176. [Google Scholar] [CrossRef]
- Chen, S.Z.; Wang, H.P.; Xu, F.; Jin, Y.Q. Target classification using the deep convolutional networks for SAR images. IEEE Trans. Geosci. Remote Sens. 2016, 47, 1685–1697. [Google Scholar] [CrossRef]
- Furukawa, H. Deep learning for target classification from SAR imagery: Data augmentation and translation invariance. arXiv, 2017; arXiv:1708.07920. [Google Scholar]
- Ding, J.; Chen, B.; Liu, H.W.; Huang, M.Y. Convolutional neural network with data augmentation for SAR target recognition. IEEE Geosci. Remote Sens. Lett. 2016, 13, 364–368. [Google Scholar] [CrossRef]
- Du, K.N.; Deng, Y.K.; Wang, R.; Zhao, T.; Li, N. SAR ATR based on displacement- and rotation- insensitive CNN. Remote Sens. Lett. 2016, 7, 895–904. [Google Scholar] [CrossRef]
- Demetrios, G.; Nikou, C.; Likas, A. Registering sets of points using Bayesian regression. Neurocomputing 2013, 89, 122–133. [Google Scholar]
- Liu, H.W.; Jiu, B.; Li, F.; Wang, Y.H. Attributed scattering center extraction algorithm based on sparse representation with dictionary refinement. IEEE Trans. Antennas Propag. 2017, 65, 2604–2614. [Google Scholar] [CrossRef]
- Cong, Y.L.; Chen, B.; Liu, H.W.; Jiu, B. Nonparametric Bayesian attributed scattering center extraction for synthetic aperture radar targets. IEEE Trans. Signal Process. 2016, 64, 4723–4736. [Google Scholar] [CrossRef]
- Ding, B.Y.; Wen, G.J. Target recognition of SAR images multi-resolution representaion. Remote Sens. Lett. 2017, 8, 1006–1014. [Google Scholar] [CrossRef]
- Ravichandran, B.; Gandhe, A.; Simith, R.; Mehra, R. Robust automatic target recognition using learning classifier systems. Inf. Fusion 2007, 8, 252–265. [Google Scholar] [CrossRef]
- Doo, S.; Smith, G.; Baker, C. Target classification performance as a function of measurement uncertainty. In Proceedings of the 5th Asia-Pacific Conference on Synthetic Aperture Radar, Singapore, 1–4 September 2015. [Google Scholar]
- Ding, B.Y.; Wen, G.J. Exploiting multi-view SAR images for robust target recognition. Remote Sens. 2017, 9, 1150. [Google Scholar] [CrossRef]
- Ding, B.Y.; Wen, G.J.; Huang, X.H.; Ma, C.H.; Yang, X.L. Target recognition in SAR images by exploiting the azimuth sensitivity. Remote Sens. Lett. 2017, 8, 821–830. [Google Scholar] [CrossRef]













| Layer Type | Image Size | Feature Maps | Kernel Size |
|---|---|---|---|
| Input | 88 × 88 | 1 | - |
| Convolution | 84 × 84 | 16 | 5 × 5 |
| Pooling | 42 × 42 | 16 | 2 × 2 |
| Convolution | 38 × 38 | 32 | 5 × 5 |
| Pooling | 19 × 19 | 32 | 2 × 2 |
| Convolution | 14 × 14 | 64 | 6 × 6 |
| Pooling | 7 × 7 | 64 | 2 × 2 |
| Full Connected | 1 × 1 | 1024 | - |
| Output | 1 × 1 | 10 | - |
| FA | ||
| MA | ||
| Class | Serial No. | Training Set | Test Set | ||
|---|---|---|---|---|---|
| Depression | No. Images | Depression | No. Images | ||
| BMP2 | 9563 | 17° | 233 | 15° | 195 |
| 9566 | 17° | 232 | 15° | 196 | |
| c21 | 17° | 233 | 15° | 196 | |
| BTR70 | c71 | 17° | 233 | 15° | 196 |
| T72 | 132 | 17° | 232 | 15° | 196 |
| 812 | 17° | 231 | 15° | 195 | |
| S7 | 17° | 228 | 15° | 191 | |
| ZSU23/4 | D08 | 17° | 299 | 15° | 274 |
| ZIL131 | E12 | 17° | 299 | 15° | 274 |
| T62 | A51 | 17° | 299 | 15° | 273 |
| BTR60 | k10yt7532 | 17° | 256 | 15° | 195 |
| D7 | 92v13015 | 17° | 299 | 15° | 274 |
| BDRM2 | E71 | 17° | 298 | 15° | 274 |
| 2S1 | B01 | 17° | 299 | 15° | 274 |
| Abbre. | Feature | Classifier | Ref. |
|---|---|---|---|
| SVM | PCA features | SVM | [30] |
| SRC | PCA features | SRC | [32] |
| A-ConvNet | Original image intensities | CNN | [39] |
| ASC | ASCs | ASC matching method | [22] |
| Class | BMP2 | BTR70 | T72 | T62 | BDRM2 | BTR60 | ZSU23/4 | D7 | ZIL131 | 2S1 | PCC (%) |
|---|---|---|---|---|---|---|---|---|---|---|---|
| BMP2 | 194 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 99.49 |
| BTR70 | 0 | 196 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 0 | 100 |
| T72 | 0 | 1 | 194 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 98.98 |
| T62 | 0 | 0 | 0 | 271 | 0 | 0 | 2 | 0 | 0 | 0 | 99.27 |
| BDRM2 | 0 | 0 | 1 | 0 | 271 | 1 | 1 | 0 | 0 | 0 | 98.91 |
| BTR60 | 0 | 1 | 0 | 1 | 0 | 193 | 0 | 0 | 0 | 0 | 98.97 |
| ZSU23/4 | 0 | 0 | 0 | 0 | 0 | 0 | 274 | 0 | 0 | 0 | 100 |
| D7 | 0 | 0 | 0 | 1 | 1 | 0 | 0 | 272 | 0 | 0 | 99.27 |
| ZIL131 | 0 | 0 | 0 | 0 | 0 | 0 | 1 | 0 | 274 | 0 | 100 |
| 2S1 | 0 | 0 | 0 | 1 | 0 | 0 | 0 | 0 | 1 | 272 | 99.27 |
| Average (%) | 99.41 | ||||||||||
| Method | Proposed | SVM | SRC | A-ConvNet | ASC |
|---|---|---|---|---|---|
| PCC (%) | 99.41 | 98.42 | 97.66 | 99.12 | 97.30 |
| Depression | BMP2 | BDRM2 | BTR70 | T72 | |
|---|---|---|---|---|---|
| Training set | 17° | 233 (Sn_9563) | 298 | 233 | 232(Sn_132) |
| Test set | 15°, 17° | 428(Sn_9566) 429(Sn_c21) | 0 | 0 | 426(Sn_812) 573(Sn_A04) 573(Sn_A05) 573(Sn_A07) 567(Sn_A10) |
| Class | Serial No. | BMP2 | BRDM2 | BTR-70 | T-72 | PCC (%) |
|---|---|---|---|---|---|---|
| BMP2 | Sn_9566 | 410 | 13 | 4 | 1 | 95.79 |
| Sn_c21 | 417 | 5 | 4 | 3 | 97.20 | |
| T72 | Sn_812 | 13 | 1 | 1 | 411 | 96.48 |
| Sn_A04 | 15 | 8 | 0 | 550 | 95.99 | |
| Sn_A05 | 12 | 2 | 2 | 557 | 97.21 | |
| Sn_A07 | 8 | 2 | 10 | 553 | 97.21 | |
| Sn_A10 | 12 | 5 | 0 | 550 | 97.00 | |
| Average (%) | 96.61 | |||||
| Method | Proposed | SVM | SRC | A-ConvNet | ASC |
|---|---|---|---|---|---|
| PCC (%) | 98.64 | 95.88 | 95.64 | 98.18 | 97.82 |
| Depression | 2S1 | BDRM2 | ZSU23/4 | |
|---|---|---|---|---|
| Training set | 17° | 299 | 298 | 299 |
| Test set | 30° | 288 | 287 | 288 |
| 45° | 303 | 303 | 303 |
| Depression | Class | Results | PCC (%) | Average (%) | ||
|---|---|---|---|---|---|---|
| 2S1 | BDRM2 | ZSU23/4 | ||||
| 30° | 2S1 | 280 | 5 | 3 | 97.22 | 97.80 |
| BDRM2 | 2 | 283 | 2 | 98.26 | ||
| ZSU23/4 | 2 | 5 | 281 | 97.57 | ||
| 45° | 2S1 | 219 | 53 | 31 | 72.28 | 76.16 |
| BDRM2 | 12 | 245 | 46 | 80.96 | ||
| ZSU23/4 | 34 | 41 | 228 | 75.25 | ||
| Method | PCC (%) | |
|---|---|---|
| 30° | 45° | |
| Proposed | 97.80 | 76.16 |
| SVM | 96.57 | 61.05 |
| SRC | 96.32 | 65.35 |
| A-ConvNet | 96.94 | 63.24 |
| ASC | 96.26 | 71.65 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Jiang, C.; Zhou, Y. Hierarchical Fusion of Convolutional Neural Networks and Attributed Scattering Centers with Application to Robust SAR ATR. Remote Sens. 2018, 10, 819. https://doi.org/10.3390/rs10060819
Jiang C, Zhou Y. Hierarchical Fusion of Convolutional Neural Networks and Attributed Scattering Centers with Application to Robust SAR ATR. Remote Sensing. 2018; 10(6):819. https://doi.org/10.3390/rs10060819
Chicago/Turabian StyleJiang, Chuanjin, and Yuan Zhou. 2018. "Hierarchical Fusion of Convolutional Neural Networks and Attributed Scattering Centers with Application to Robust SAR ATR" Remote Sensing 10, no. 6: 819. https://doi.org/10.3390/rs10060819
APA StyleJiang, C., & Zhou, Y. (2018). Hierarchical Fusion of Convolutional Neural Networks and Attributed Scattering Centers with Application to Robust SAR ATR. Remote Sensing, 10(6), 819. https://doi.org/10.3390/rs10060819