High Temporal Resolution Refractivity Retrieval from Radar Phase Measurements
Abstract
:1. Introduction
2. Study Site and Data Sources
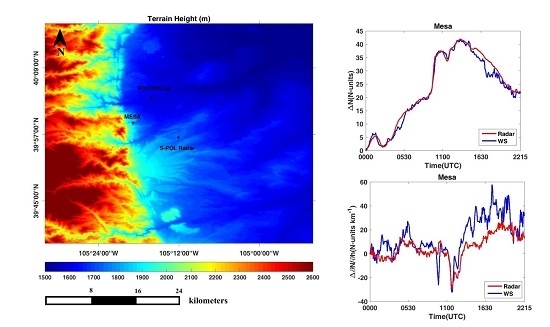
2.1. Study Area
2.2. Data Sources
3. High Temporal Resolution Estimation of Mean Refractivity and Refractivity Vertical Gradient over Small Areas
3.1. Radar Refractivity Algorithm
3.2. Joint Estimation of the Refractive Index and the Refractive Index Vertical Gradient Variations
4. Results
4.1. Refractivity from Automatic Weather Stations
4.2. Stationarity Index of a Target
4.3. Refractivity from Radar Phase Measurements
5. Discussion
6. Conclusions
Author Contributions
Acknowledgments
Conflicts of Interest
Abbreviations
| REFRACTT | Refractivity Experiment for HO Research and Collaborative Operational Technology Transfer |
| PPI | Plan Position Indicator |
| LS | Least Squares |
| RI | Reliability Index |
| UTC | Universal Time Coordinated |
| DEM | Digital Elevation Model |
| RMSE | Root Mean Square Error |
Appendix A. Analysis of the Contributions to the Phase
Appendix A.1. Horizontal Contribution


Appendix A.2. Vertical Contribution


Appendix A.3. Earth’s Curvature Contribution

References
- Weckwerth, T.M.; Wilson, J.W.; Wakimoto, R.M. Thermodynamic variability within the convective boundary layer due to horizontal convective rolls. Mon. Weather Rev. 1996, 124, 769–784. [Google Scholar] [CrossRef]
- Ziegler, C.L.; Lee, T.J.; Pielke, R.A. Convective initiation at the dryline: A modeling study. Mon. Weather Rev. 1997, 125, 1001–1026. [Google Scholar] [CrossRef]
- Crook, N.A. Sensitivity of moist convection forced by boundary layer processes to low-level thermodynamic fields. Mon. Weather Rev. 1996, 124, 1767–1785. [Google Scholar] [CrossRef]
- Weckwerth, T.M. The effect of small-scale moisture variability on thunderstrom initiation. Mon. Weather Rev. 2000, 128, 4017–4030. [Google Scholar] [CrossRef]
- Deeter, M.N.; Evans, K.F. Mesoscale variations of water vapor inferred from millimeter-wave imaging radiometer during TOGA COARE. J. Appl. Meteorol. Notes Corresp. 1997, 36, 183–188. [Google Scholar] [CrossRef]
- Dabberdt, W.F.; Schlatter, T.W. Research Opportunities from Emerging Atmospheric Observing and Modeling Capabilities. Bull. Am. Meteorol. Soc. 1996, 77, 305–323. [Google Scholar] [CrossRef] [Green Version]
- Weckwerth, T.M.; Pettet, C.R.; Fabry, F.; Park, S.; LeMone, M.A.; Wilson, J.W. Radar refractivity retrieval: validation and application to shrot-term forecasting. J. Appl. Meteorol. 2005, 44, 285–300. [Google Scholar] [CrossRef]
- Fabry, F. The Spatial Variability of Moisture in the Boundary Layer and its Effect on Convection Initiation: Project-Long Characterization. Mon. Weather Rev. 2006, 134, 978–987. [Google Scholar] [CrossRef]
- Matzler, C. Parabolic Equations for Wave Propagation and the Advanced Atmospheric Effects Prediction System; Institute of Applied Physics, University of Bern: Bern, Switzerland, 2004. [Google Scholar]
- Levy, M.F. Horizontal parabolic equation solution of radiowave propagation problems on large domains. IEEE Trans. Antennas Propag. 1995, 43, 137–144. [Google Scholar] [CrossRef]
- Barrios, A.E. A terrain parabolic equation model for propagation in the troposphere. IEEE Trans. Antennas Propag. 1994, 42, 90–98. [Google Scholar] [CrossRef]
- Dockery, G.D. Modeling electromagnetic wave propagation in the troposphere using the parabolic equation. IEEE Trans. Antennas Propag. 1988, 36, 1464–1470. [Google Scholar] [CrossRef]
- Ozgun, O. Recursive two-way parabolic equation approach for modeling terrain effects in tropospheric propagation. IEEE Trans. Antennas Propag. 2009, 57, 2706–2714. [Google Scholar] [CrossRef]
- Liang, Y.C.; Chen, K.C.; Li, Y.G.; Mahonen, P. Cognitive Radio Networking and Communications: An overview. IEEE Trans. Veh. Technol. 2011, 60, 3386–3407. [Google Scholar] [CrossRef]
- Bevis, M.; Businger, S.; Herring, T.A.; Rocken, C.; Anthes, R.A.; Ware, R.H. GPS Meteorology: Remote Sensing of Atmospheric Water Vapor Using the Global Positioning System. J. Geophys. Res. 1992, 97, 15787–15801. [Google Scholar] [CrossRef]
- Businger, S.; Chriswell, S.; Bevis, M.; Duan, J.; Anthes, R.; Rocken, C.; Ware, H.; Exner, M.; VanHove, T.; Solheim, F. The Promise of GPS in Atmospheric Monitoring. Bull. Am. Meteorol. Soc. 1996, 77, 5–18. [Google Scholar] [CrossRef] [Green Version]
- Fabry, F.; Frush, C.; Zawadzki, I.; Kilambi, A. On the extraction of near-surface index of refraction using radar phase measurements from ground targets. J. Atmos. Ocean. Technol. 1997, 14, 978–987. [Google Scholar] [CrossRef]
- Fabry, F. Meteorological Value of Ground Target Measurements. J. Atmos. Ocean. Technol. 2004, 21, 560–573. [Google Scholar] [CrossRef]
- Weckwerth, T.M.; Parson, D.B.; Koch, S.E.; Moore, J.A.; LeMone, M.A.; Demoz, B.B.; Flamant, C.; Geerts, B.; Wang, J.; Feltz, W.F. An overview of the International H2O Project (IHOP_2002) and some preliminary highlights. Bull. Am. Meteorol. Soc. 2004, 85, 253–277. [Google Scholar] [CrossRef]
- Roberts, R.D.; Fabry, F.; Kennedy, P.C.; Nelson, E.; Wilson, J.; Rehak, N.; Fritz, J.; Chandrasekar, V.; Braun, J.; Sun, J.; et al. REFRACTT_2006: Real-Time retrieval of high-resolution low-level moisture fields from operational NEXRAD and research radars. Bull. Am. Meteorol. Soc. 2008, 89, 1535–1548. [Google Scholar] [CrossRef]
- Bodine, D.; Heinselman, P.L.; Cheong, B.L.; Michaud, D.; Palmer, R.D. A case study on the impact of Moisture Variability on Convection Initiation using Radar Refractivity Retrievals. J. Appl. Meteorol. Climatol. 2010, 49, 1766–1778. [Google Scholar] [CrossRef]
- Bodine, D.; Michaud, D.; Palmer, R.D.; Heinselman, P.L.; Brotzge, J.; Gasperoni, N.; Cheong, B.L.; Xue, M.; Gao, J. Understanding Radar Refractivity: Sources of Uncertainty. J. Appl. Meteorol. Climatol. 2011, 50, 2543–2560. [Google Scholar] [CrossRef] [Green Version]
- Nicol, J.C.; Illingwoth, A.; Darlington, T.; Kitchen, M. Quantifying Errors due to Frequency Changes and Target Location Uncertainty for Radar refractivity Retrievals. J. Atmos. Ocean. Technol. 2013, 30, 2006–2024. [Google Scholar] [CrossRef]
- Parent du Chatelet, J.; Tabary, P.; Boudjabi, C. Evaluation of the refractivity measurement feasibility with a C-Band radar equipped with a magnetron transmitter. In Proceedings of the 33rd International Conference on Radar Meteorology, Cairns, Australia, 6–10 August 2007. [Google Scholar]
- Besson, L.; Boudjabi, C.; Caumont, O.; Parent du Chatelet, J. Links between Weather Phenomena and Characterisitcs of Refractivity Measured by Precipitation Radar. Bound. Layer Meteorol. 2011, 143, 77–95. [Google Scholar] [CrossRef]
- Nicol, J.C.; Illingwoth, A.; Bartholomew, K. The potential of 1h refractivity changes from an operational C-Band magnetron-based radar for numerical weather prediction validation and data assimilation. Q. J. R. Meteorol. Soc. 2014, 140, 1209–1218. [Google Scholar] [CrossRef]
- Cheong, B.L.; Palmer, R.; Chandrasekar, V.; Junyent, F. Real-time Refractivity Retrieval Using the Magnetron-based CASA X-band Radar Network during the Spring 2008 Campaign. In Proceedings of the International Geoscience and Remote Sensing Symposium (IGARSS), Boston, MA, USA, 6–11 July 2008. [Google Scholar]
- Cheong, B.L.; Palmer, R.; Curtis, C.D.; Yu, T.Y.; Zrnic, D.S.; Forsyth, D. Refractivity Retrieval Using the Phased-Array Radar: First Results and Potencial for Multimission Operation. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2527–2537. [Google Scholar] [CrossRef]
- Parent du Chatelet, J.; Boudjabi, J.; Boudjabi, C. A new formulation for signal reflected from a target using a magnetron radar. In Proceedings of the ERAD 2008—The 5th European Conference on Radar in Meteorology and Hydrology, Helsinki, Finland, 30 June–4 July 2008. [Google Scholar]
- Junyent, F.; Chandrasekar, V.; McLaughlin, D.; Insanic, E.; Bharadwaj, N. The CASA Integrated Project 1 Networked Radar System. J. Atmos. Ocean. Technol. 2010, 27, 61–78. [Google Scholar] [CrossRef]
- Parent du Chatelet, J.; Boudjabi, C.; Besson, L.O.C. Errors caused by long-term drifts of magnetron frequencies for refractivity measurement with a radar: Theoretical formulation and initial validation. J. Atmos. Ocean. Technol. 2012, 29, 1428–1434. [Google Scholar] [CrossRef]
- Nicol, J.C.; Illingwoth, A. The effect of Phase-Correlated Returns and Spatial Smoothing on the Accuracy of Radar Refractivity Retrievals. J. Atmos. Ocean. Technol. 2013, 30, 22–39. [Google Scholar] [CrossRef]
- Besson, L.; Parent du Chatelet, J. Solutions for Improving the Radar Refractivity Measurements by taking Operational Constraints into Account. Bound. Layer Meteorol. 2013, 30, 1730–1742. [Google Scholar] [CrossRef]
- Rogers, L.T.; Hattan, C.; Stapleton, J. Estimating evaporation duct heights from radar sea echo. Radio Sci. 2000, 35, 955–966. [Google Scholar] [CrossRef] [Green Version]
- Gerstoft, P.; Rogers, L.; Krolik, J.L.; Hodgkiss, W. Inversion for refractivity parameters from radar sea clutter. Radio Sci. 2003, 38. [Google Scholar] [CrossRef] [Green Version]
- Zhao, X.; Huang, S. Estimation of atmospheric duct structure using radar sea clutter. J. Atmos. Sci. 2012, 69, 2808–2818. [Google Scholar] [CrossRef]
- Karimian, A.; Yardim, C.; Gerstoft, P.; Hodgkiss, W.; Barrios, A.E. Refractivity estimation from sea clutter: An invited review. Radio Sci. 2011, 46. [Google Scholar] [CrossRef] [Green Version]
- Park, S.; Fabry, F. Simulation and interpretation of the phase data used by radar refractivity retrieval algorithm. J. Atmos. Ocean. Technol. 2010, 27, 1286–1301. [Google Scholar] [CrossRef]
- Park, S.; Fabry, F. Estimation of Near-Ground Propagation Conditions using Radar Ground Echo Coverage. J. Atmos. Ocean. Technol. 2011, 28, 165–180. [Google Scholar] [CrossRef]
- Feng, Y.; Fabry, F.; Weckwerth, T.M. Improving Radar Refractivity Retrieval by considering the change in the Refractivity Profile and the Varying Altitudes of Ground Targets. J. Atmos. Ocean. Technol. 2016, 33, 989–1004. [Google Scholar] [CrossRef]
- ITU-R, P.; 453-11, R. The Radio Refractive Index: Its Formula and Refractivity Data. 2015. Available online: https://www.itu.int/dmspubrec/itu-r/rec/p/R-REC-P.453-11-201507-S!!PDF-E.pdf (accessed on 6 June 2018).
- UCAR/NCAR. Earth Observing Laboratory. S-Band/Ka-Band Polarimetric (S-PolKa) Data cfRadial Format. Version 1.0. UCAR/NCAR—Earth Observing Laboratory. 1996. Available online: https://doi.org/10.5065/D6WW7FV6 (accessed on 11 January 2015).
- Lutz, J.P.; Lewis, E.; Loew, E.; Randall, M.; Van Andel, J. NCAR SPol: Portable polarimetric S-Band radar. In Proceedings of the Preprints, Ninth Symposium on Meteorological Observations and Instrumentation, Charlotte, NC, USA, 27–31 March 1995; pp. 408–410. [Google Scholar]
- Bean, B.R.; Dutton, E.J. Radio Meteorology. In National Bureau of Standards Monograph; National Bureau of Standards: Gaithersburg, MD, USA, 1968; 435p. [Google Scholar]
- Doviak, R.J.; Zrnic, D.S. Doppler Radar and Weather Observations, 2nd ed.; Academy Press Inc.: Cambridge, MA, USA, 2006; 562p. [Google Scholar]
- Ferreti, A.; Prati, C.; Rocca, F. Permanent scatterers in SAR interferometry. IEEE Trans. Geosci. Remote Sens. 2001, 39, 8–20. [Google Scholar] [CrossRef] [Green Version]
- Noferiny, L.; Pieraccini, D.; Mecatti, D.; Luzi, G.; Atzeni, C.; Tambburini, A.M.B. Permanent Scatterers Analysis for Atmospheric Correction in Ground-Based SAR Interferometry. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1459–1470. [Google Scholar] [CrossRef]







| Parameter | Value |
|---|---|
| Frequency | 2.8 GHz |
| Wavelength | 10 cm |
| Pulse-width | 0.994 s |
| Pulse repetition frequency (PRF) | 655–714 Hz |
| Range resolution | 150 m |
| Beam-width | 0.918 |
| Scan-rate | 11.13–12.14s |
| Samples | 54 |
| Scanning elevation angle | 0–0.5 |
| Noise Power | dBm |
| Station | Longitude | Latitude | Altitude (m) | Distance to Radar (km) | Azimuth () | Gate |
|---|---|---|---|---|---|---|
| S-pol Radar | 10511′42 W | 3957′00 N | 1742 | – | – | – |
| Mesa | 10516′42 W | 3958′48 N | 1885 | 7.578 | 295.9 | 51 |
| Foothills | 10514′35 W | 4001′48 N | 1625 | 9.777 | 335.3 | 69 |
| Source | Data Collecting Time (UTC) | Samples | Resolution |
|---|---|---|---|
| Radar | 0000 to 2215 on 1 August 2006 | 356 PPIs | <4 min |
| Weather Stations | 267 Observations (T, p and e) | 5 min |
| Estimator | Parameter | Mesa | Foothills |
|---|---|---|---|
| N () | RMSE | 1.91 | 1.79 |
| BIAS | |||
| N () | RMSE | 1.65 | 3.00 |
| BIAS | 0.68 | ||
| RMSE | 15.37 | 15.90 | |
| BIAS | 10.50 | 10.67 |
© 2018 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
López, R.N.; Río, V.S.d. High Temporal Resolution Refractivity Retrieval from Radar Phase Measurements. Remote Sens. 2018, 10, 896. https://doi.org/10.3390/rs10060896
López RN, Río VSd. High Temporal Resolution Refractivity Retrieval from Radar Phase Measurements. Remote Sensing. 2018; 10(6):896. https://doi.org/10.3390/rs10060896
Chicago/Turabian StyleLópez, Rubén Nocelo, and Verónica Santalla del Río. 2018. "High Temporal Resolution Refractivity Retrieval from Radar Phase Measurements" Remote Sensing 10, no. 6: 896. https://doi.org/10.3390/rs10060896
APA StyleLópez, R. N., & Río, V. S. d. (2018). High Temporal Resolution Refractivity Retrieval from Radar Phase Measurements. Remote Sensing, 10(6), 896. https://doi.org/10.3390/rs10060896