Multi-Criteria Evaluation of Snowpack Simulations in Complex Alpine Terrain Using Satellite and In Situ Observations

Abstract

This work presents an extensive evaluation of the Crocus snowpack model over a rugged and highly glacierized mountain catchment (Arve valley, Western Alps, France) from 1989 to 2015. The simulations were compared and evaluated using in-situ point snow depth measurements, in-situ seasonal and annual glacier surface mass balance, snow covered area evolution based on optical satellite imagery at 250 m resolution (MODIS sensor), and the annual equilibrium-line altitude of glaciers, derived from satellite images (Landsat, SPOT, and ASTER). The snowpack simulations were obtained using the Crocus snowpack model driven by the same, originally semi-distributed, meteorological forcing (SAFRAN) reanalysis using the native semi-distributed configuration, but also a fully distributed configuration. The semi-distributed approach addresses land surface simulations for discrete topographic classes characterized by elevation range, aspect, and slope. The distributed approach operates on a 250-m grid, enabling inclusion of terrain shadowing effects, based on the same original meteorological dataset. Despite the fact that the two simulations use the same snowpack model, being potentially subjected to same potential deviation from the parametrization of certain physical processes, the results showed that both approaches accurately reproduced the snowpack distribution over the study period. Slightly (although statistically significantly) better results were obtained by using the distributed approach. The evaluation of the snow cover area with MODIS sensor has shown, on average, a reduction of the Root Mean Squared Error (RMSE) from 15.2% with the semi-distributed approach to 12.6% with the distributed one. Similarly, surface glacier mass balance RMSE decreased from 1.475 m of water equivalent (W.E.) for the semi-distributed simulation to 1.375 m W.E. for the distribution. The improvement, observed with a much higher computational time, does not justify the recommendation of this approach for all applications; however, for simulations that require a precise representation of snowpack distribution, the distributed approach is suggested.

1. Introduction

The dynamics of the accumulation and melting of snow and ice in mountain areas has major effects on the timing and level of discharge from rivers in downstream areas. One-sixth of the Earth’s population depends directly on the water supply from snow and ice melt in mountain areas [1]. Thus, significant research effort has been applied to the study of snow and ice dynamics in these regions [2,3,4,5], with particular focus on mountain hydrology [6,7,8,9]. The snowpack dynamics and its spatial extent also control many mountain processes, including soil erosion, plant survival [10], and glacier surface mass balance [11,12,13].

Some of the most dangerous natural hazards in mountain areas are also directly related to the distribution of the snowpack and ice, and their evolution over time. This is the case for snow avalanches [14], and floods in mountain rivers and downstream areas [15]. To enable anticipation of the occurrence of snow-related hazards and to reduce the threat to populations and infrastructure [16,17]; various models have been developed to reproduce and forecast the evolution of the snowpack on a daily or sub-daily basis.

Detailed snowpack models [18,19] are increasingly used together with hydrological models to simulate river discharges, and this depends on reliable simulation of snow and ice melting [20,21,22]. The more accurate the information on snowpack dynamics, the more accurate the discharge forecasts based on hydrological models. However, the spatio-temporal distribution of the snowpack is highly variable in mountain areas [4,23,24], and the runoff from mountain catchments depends on many interrelated processes that are highly variable in space and time, including infiltration, surface runoff, groundwater recharge, freezing of soil, and the snowpack distribution [25]. For example, in areas where snow persists throughout the year, the snowpack dynamics has a major impact on groundwater storage [26]. Finally, snowpack models are also combined with other models and techniques to forecast avalanche hazards [18,27].

Reproducing snowpack dynamics in heterogeneous mountain areas remains challenging. Some snowpack processes, including wind-induced redistribution and small scale topographic control on the snow distribution [28,29,30,31,32] have not yet been fully integrated into numerical snowpack models which can be used operationally. Moreover, the additive nature of snowpack dynamics involves discrepancies between observed and simulated snowpacks, which can accumulate over the simulation period (e.g., [33]).

The various approaches available for running snowpack simulations range from punctual simulations (snowpack dynamics simulated for a particular location having specific characteristics) to semi-distributed and distributed approaches that simulate snow dynamics over broad areas.

The semi-distributed approach, based on an unstructured grid design, involves simulating the snowpack evolution over areas defined using discrete values for topographic variables including altitude, aspect, and slope [34,35]. The French numerical chain S2M (SAFRAN-SURFEX/ISBA-Crocus-MEPRA; [36]), simulates the snowpack evolution using a semi-distributed approach. In this chain the SURFEX/ISBA-Crocus snowpack model ([19]; hereafter referred to as Crocus) is applied over a semi-distributed discretization of the French mountain ranges for various topographic classes. Semi-distributed hydrological simulations are also widely used, which involve discretizing catchments into hydrologic response units (HRU), with the flow contribution from the HRUs being routed and compounded into an overall catchment discharge [37]. This simulation method is also applied to river discharge simulations in mountain areas, with the output of semi-distributed snowpack simulations used as inputs to the hydrological models [21].

The other modeling approach to simulating snowpack dynamics over extended areas is distributed simulations. This method involves simulation of the temporal evolution of environmental variables (e.g., snowpack or other hydrological variables) over a gridded representation of the terrain. In this approach the terrain is not discretized in classes. Rather, it explicitly considers the characteristics (e.g., elevation, slope, aspect) for each pixel when simulating its snowpack evolution.

Distributed and semi-distributed approaches have advantages and disadvantages, particularly the lower computing resource requirements of semi-distributed simulations, and the fact that terrain representation of distributed simulations is closer to reality. Some snowpack processes cannot be accurately reproduced using the semi-distributed approach, including wind-induced snow redistribution, small scale topographic control of precipitation, and terrain shadowing effects [32,38,39]. However, evaluating the performance of these simulation approaches depends on the intended use of the simulations [40,41]. Similarly, the results obtained will depend on the spatial scale and the quality of the meteorological forcing model, and whether it is distributed or semi-distributed [42,43].

As far as the authors know, no attempt to compare distributed and semi-distributed snowpack simulations results has been made to date. This is significant because the implementation of the most promising advances in simulation is mainly considered for distributed simulations. This is the case for assimilation of satellite data [44,45,46]; the inclusion of small scale processes in simulations, including snow redistribution by wind [30,32]; and gravitational or topographic controls on snow movements [29,47,48]. Semi-distributed simulations may also allow the implementation of satellite data assimilation techniques (as suggested in [49]) but would require specific methods for aggregating observations into the semi-distributed clustering of the simulation domain and they would reduce potential benefits of high resolution satellite observations.

The impact of effects solely arising from the representation of the topography on snowpack simulations has not yet been assessed in detail. For example, the influence of terrain shadowing effects on Crocus model outputs, allowed in distributed simulations of sufficiently high spatial resolution, has not been analyzed specifically.

Optical remote sensing data are increasingly used to extensively evaluate snowpack simulations over large areas and for long time periods [42,50,51]. However, such data do not provide detailed information about snowpack bulk variables such as snow depth and snow water equivalent [52,53,54] and thus must be combined with in-situ observations to provide a complete evaluation, such as the snow depth evolution observed with automatic weather stations or glacier surface mass balance.

The main goal of this work is to study of the impact on the Crocus snowpack model simulation of including terrain shadowing effects by comparing semi-distributed simulations (which do not include terrain shadowing) and distributed simulations (which include terrain shadowing). The upper Arve catchment (French Alps) was selected as the study area, since it is characterized by a high spatial heterogeneity with an important altitudinal gradient and the presence of large glaciated areas. The evaluation is based on the analysis of the Crocus model capabilities on simulating different snowpack variables (mainly snow depth, snow water equivalent and snow covered area) compared with in-situ observations as well as remote sensing observations. Consequently, we assessed the ability of the model to simulate the snowpack evolution using a multi-criteria approach (e.g., Hanzer et al., 2016). This way, we firstly assessed the ability of the model to simulate the snowpack evolution at a local scale for specific stations having continuous snow observation data. These punctual simulations enabled initial analysis of the capacity of the model to subsequently evaluate the distributed and semi-distributed approaches to simulating the snowpack dynamics over a broader area. The simulation results from both approaches were compared with observations for the snow covered area based on MODIS satellite sensors, the glacier surface mass balance (winter, summer, and annual), and the glacier equilibrium-line altitude derived from satellite images (Landsat, SPOT, and ASTER). This enabled assessment of the use of semi-distributed or distributed simulations for analysis of snow and ice dynamics. The simulations were based on data for the upper Arve catchment for the 26 years from 1989 to 2015.

2. Study Area and Period

The upper Arve catchment is located in the western Alps, France, between the northeast slopes of the Mont Blanc massif and the southwest slopes of the Aiguilles Rouges massif. The catchment extends from the headwaters of the Arve River to the town of Chamonix (Figure 1), and includes major tributaries carrying melt water from three glacierized areas (Arveyron de la Mer de Glace, Arveyron d’Argentière, and Bisme du Tour) to the main river. The upper Arve catchment covers 205 km² and has a high degree of topographic heterogeneity, with steep slopes in some areas, and gentle slopes on large glacierized areas and at the lower elevation zones of the valley, which is a typical U-shaped glacial valley. Elevation ranges from 1020 to 4225 m.a.s.l., with 65% of the surface area above 2000 m.a.s.l. Glaciers cover 33% of the area [55], and 22% is covered by forests, mainly in the lower elevation areas. Chamonix climatology is classified as a Cfb Köpen-Geiger type with a mean annual precipitation of 1055 mm., and a mean annual temperature of 7.3 °C (observed in the 1981–2015 time period). The water discharge regime is strongly dependent on the snow melt dynamics during spring and early summer, with the major contribution of melt water from glacierized areas occurring during late summer and autumn; this is termed a nivo-glacial regime of river discharge [56]. The Mont Blanc and Aiguilles Rouges massifs are also highly spatially heterogeneous, having various slopes and aspects over a wide range of elevations in glacierized and non-glacierized areas; this affects the spatio-temporal evolution of snow and ice.

The area is subject to severe flood hazard. This is a consequence of the steepness of the terrain, which results in a rapid hydrological response to precipitation, the typically rapid meteorological changes that occur in this mountain area (mainly associated with convective episodes during spring and summer). Such hazards are particularly significant in the town of Chamonix in the bottom of the valley, featuring high population densities and infrastructure especially in summertime at the peak of the tourism season. The study period spams from 1989 to 2015 in order to evaluate simulations with different seasonal conditions.

3. Observation Datasets

3.1. Punctual Snow Depth Observations

The Météo-France observation network has 5 stations in the study area (Figure 1), located at different elevations. Some of these stations acquired data during all snow seasons throughout the entire study period, including the Nivose Aiguilles Rouges (2365 m.a.s.l.), Chamonix (1025 m.a.s.l.), and Le Tour (1470 m.a.s.l.) automated stations. The other two stations started measurements later, and provided manual observational data since the 1994–1995 snow season (Lognan station; 1970 m.a.s.l) and since the 2003–2004 snow season (La Flegere station; 1850 m.a.s.l.). At these stations the temporal evolution of the snow depth was observed at daily or sub-daily time intervals, and these data were used to evaluate SAFRAN–Crocus in non-glacierized areas during winter and spring (periods with snow presence).

3.2. Snow Cover Area Distribution Based on the MODIS Sensor

3.2.1. Processing of the MODIS Data to Estimate the Snow Covered Area

Many studies have demonstrated the usefulness of MODIS images for snow cover mapping in mountain areas [52,53,57]. The MODIS mission database provides long temporal coverage (the mission was launched in 2000, and obtains daily images), which enabled a comparison between the simulated and observed snow cover evolution for 14 snow seasons (out of the 26) simulated on an almost daily basis (comparisons were limited by cloud cover in the study area). Sub-pixel snow monitoring of the snow cover at 250-m spatial resolution was performed using MODImLab software, designed specifically to address the effect of complex terrain on the satellite signal. The processing chain is described in [58,59]. Multispectral fusion between MOD02HKM (500 m; bands 3–7) and MOD02QKM (bands 1 and 2) [60], enable this software to generate images at 250 × 250 m spatial resolution to derive various snow and ice products. MODImLab snow products have been already validated with Landsat [59] and SPOT [61] optical imagery showing a strong agreement.

We used the unmixing_wholesnow (UWS, [62]) product, as it has been shown to outperform other snow and ice products for assessing the evolution of the Snow Covered Area (SCA) using a spectral unmixing technique developed by [50]. We also considered the cloudiness product in MODImLab to determine the fraction of the catchment affected by cloud cover. The generation of the UWS and cloudiness products in MODImLab software was based on the same DEM used for the snowpack simulations. This ensured a direct match between of observation and simulation pixels. To avoid errors related to cloud presence in the study area, only days having cloud cover representing <20% of the total surface area were considered in the analysis. With this threshold, 54% of the available MODIS images during the study period were discarded. Despite the fact that for particularly short time periods the limitations of the availability of MODIS images did not enable the evaluation of SCA, the seasonal and annual evaluation performed in this work are not affected by these potential limitations. For the worst winter season (in terms of MODIS data availability), at least a 43% of dates are included, thereby having a temporal distribution that enables an appropriate evaluation.

3.2.2. Thresholds to Assess whether a Pixel is Snow-Covered in MODIS Images and from Model Output on the 250 m × 250 m Grid

Different thresholds of the unmixing_wholesnow (UWS) MODImLab product were considered in order to distinguish whether a pixel is snow covered. The UWS values used in the sensibility test were 0.25, 0.35 and 0.45. Similarly, three simulated snow depth threshold values (0.10, 0.15, and 0.20 m [42,52] were examined to consider a pixel as snow-covered in the simulations as a sensitivity test.

3.3. Glacier Surface Mass Balance

Glaciers located in the Mer de Glace and Argentière sub-catchments have been monitored, in a sufficient number of measurement locations for our analysis, since 1995 by the French Service National d’Observation GLACIOCLIM. During this period, field data were obtained twice per year, during the maximum (end April–May) and minimum (around October) snow accumulation periods. These data enabled calculation of the surface mass balance (SMB) for summer (annual difference between the maximum and minimum acquisitions), winter (annual difference between the minimum of the previous year and the maximum acquisitions), and annually (year to year differences in the minimum acquisitions) at each individual point of the network (Figure 2). The observation procedure involves the use of glaciological methods [63] to retrieve the surface mass balance for the various time periods. Stakes (markers over the glaciers) are set up in both accumulation and ablation areas throughout the glaciers, and reflect the evolution of the various zones of the glaciers. The spatial distribution of the stakes is shown in Figure 2. For further information on the methods for SMB data collection, see [12].

3.4. Glacier Equilibrium-Line Altitude

The glacier equilibrium-line altitude (ELA) is the annual maximum elevation of the snow-ice transition over glacierized areas. Since 1984 the temporal evolution of the ELA for the five largest glaciers in the study area has been estimated using various satellite sensors [64,65]. Data on the inter-annual evolution of the ELA for the Tour, Argentière, and Mer de Glace glaciers (and its main tributaries, the Leschaux and Talèfre glaciers) was available for the entire study period, based on images from Landsat 4TM, 5TM, 7 ETM+, SPOT 1–5, and ASTER. The spatial resolution of these images ranges from 2.5 to 30 m. The method of snow line delineation using multispectral images combining green, near-infrared, and short-wave infrared bands has been fully described by [66]. The satellite acquisition date depends on various factors including the availability of satellite images for the study area and cloud presence, but images obtained during the period of minimum snow accumulation (late August to early October) were used to obtain the ELA.

4. Methods

4.1. Simulation Setup

We used the Crocus snowpack model to simulate the temporal evolution of snow and ice in the upper Arve catchment. Crocus is a multilayer model that simulates snowpack evolution based on the energy and mass exchanges between the various snow layers within the snowpack, and between the snowpack and its interface with the atmosphere and the soil (i.e., the top and bottom of the snow column). Crocus snowpack model includes the simulation of snow microstructure and their evolution based on semi-quantitative notions as sphericity and dendriticity of snow grains, providing high detail on the evolution of internal snowpack properties. The model was developed [67] as a one-dimensional multilayer physical scheme, simulating energy and mass transfers (radiative balance, turbulent heat, ground heat flux…). The simulated snowpack is vertically discretized in a maximum of 50 layers. Different rules are designed to develop a realistic of snowpack layering. Crocus is implemented in the externalized surface model SURFEX [19]. Within SURFEX [68], Crocus is coupled to the multilayer land surface model ISBA-DIF (Interaction between Soil, Biosphere and Atmosphere; diffusion version; [69].

The meteorological forcing required to drive the temporal evolution of the simulations was obtained from the SAFRAN meteorological reanalysis [27,70]. This provides the atmospheric variables needed to run Crocus at hourly time step, including air temperature, specific humidity, long wave radiation, direct and diffuse short-wave radiation, wind speed, and precipitation phase and rate. SAFRAN was specifically developed to provide meteorological forcing for mountain areas at a suitable altitudinal resolution for performing snowpack simulation addressing the impact of elevation differences on snow conditions for particular terrain classes. SAFRAN and Crocus have been applied for several decades in French mountain regions, contributing to operational avalanche warning and snow monitoring activities of Météo-France, in a semi-distributed mode [36,70].

The SAFRAN meteorological reanalysis system provides outputs for punctual simulations, or semi-distributed outputs. In the first case the analysis is performed directly for the elevations of the points of interest, and takes into account the direct solar radiation masks associated to the surrounding topography. In the semi-distributed mode, SAFRAN outputs are provided for 300-m elevation bands. The spatial extent of this analysis is approximately 1000 km². This corresponds roughly to the spatial domain from which in-situ meteorological observations are used to generate the reanalysis product. These regions are referred to as “massifs” [27,70]. This study uses only the Mont-Blanc massif, which covers the entire study catchment.

4.2. Punctual, Semi-Distributed, and Distributed Approaches

The temporal evolution of snow and ice was simulated using punctual, semi-distributed, and distributed approaches, based on the same meteorological forcing and using the same Crocus model version. In order to compare the outcome of the two spatialized simulation strategies, their results are either produced natively on a 250 m grid, or either distributing the semi-distributed SAFRAN–Crocus model runs onto the 250 m grid using the corresponding topographical classes. This spatial resolution was selected because it renders slopes sufficiently well to describe small valleys with significant shadowing effects. The 250 m grid cell size of the simulations also enables a direct comparison with optical satellite products at the same spatial resolution. It will also allow for exploring snow mechanical stability in future avalanche hazard forecasting applications, with slope at this resolution being steep enough for avalanche.

4.2.1. Punctual Simulation

Punctual snowpack simulations were performed for the five Météo-France meteorological and snow observing stations within the study area, based on the elevation, slope, and aspect for each station. Punctual simulations included a topographic mask from a 50-m digital elevation model (DEM) from the French Geographical Institute (Institut National de l’information Géographique et forestière), to account for any terrain shadowing effect on simulation of the incoming shortwave radiation. For the location of each of these five meteorological stations a separate snowpack simulation was obtained. Each of these simulations was run with the specific characteristics of its location, forcing Crocus model with the meteorological forecast extracted for the specific position of the station.

4.2.2. Semi-Distributed Simulation

Semi-distributed simulations were carried out based on the following topographic classes:

• altitude: 300-m elevation bands from 900 m.a.s.l. to 4100 m.a.s.l
• aspect: eight aspect classes (north, northeast, east, southeast, south, southwest, west, and northwest)
• slope: flat terrain, 20° and 40°

These topographic classes are the same as those used for snow monitoring and avalanche forecasting [36]. To consider snow and ice evolution on glacierized and non-glacierized areas, two distinct simulations were run for all terrain classes, one initialized using bare ground, and another involving a given thickness of ice to initialize the simulation on glacierized areas (see Section 4.3).

In a final stage, the snowpack semi-distributed simulations (which have an unstructured grid design) were assigned or re-projected onto the pixels of 250 × 250 m grid used for the distributed simulations). The pixels were categorized according to the semi-distributed terrain classes: slopes from 0° to 10° were considered flat, those from 10 to 30° were assigned to the 20° slope class, and those higher than 30° were assigned to the 40° class. From this categorization of the DEM, the snowpack simulation outputs were assigned to each terrain class for all time steps. Therefore, for each time step, a snow and ice distribution map was generated, which distributed the semi-distributed snowpack simulation obtained for the various terrain classes.

4.2.3. Distributed Simulation

The distributed snowpack simulations were performed in a DEM having 250 × 250 m grid spacing over the study area. The altitudinal resolution of SAFRAN elevation bands was defined to account for substantial changes on snowpack conditions to forecast avalanche hazard in a semi-distributed configuration. This meteorological forcing was spatially distributed over the 250-m grid DEM as follows: For each pixel of the 250-m grid, the meteorological variables at a given altitude were linearly interpolated between the closest 300-m elevation bands of the SAFRAN reanalysis, following [43].

The distributed Crocus simulations were performed, accounting for the elevation, aspect, slope but also soil, and land cover characteristics for each pixel derived from ECOCLIMAP-II/Europe;. This surface database combines the information of CLC 2000 (Corine Land Cover) and GLC2000 (Global Land Cover). Moreover, it includes information of the leaf area index from MODIS observations and the normalized difference vegetation index from SPOT, derived from the 1999 to 2005 time period [71]. ECOCLIMAP-II/Europe is only used in one time step for the initialization of soil. Topographic shadowing effect of short wave radiation [29] was accounted for in the distributed simulations. The inclusion of particular pixel features and topographic shadowing are the main differences between the semi-distributed and distributed simulations. Figure 3 shows a schematic representation of distributed and semi-distributed approaches.

4.3. Modeling of Glacierized Areas

As Crocus is a multilayer snowpack model that simulates the energy and mass exchanges between the various snowpack layers, it also enables simulation of the glacier surface mass balance [58,72,73,74]. However, the model does not simulate glacier dynamics. The extent of glacierized areas was based on the most recent data on their surface area, inventoried in 2012 [65]. Although other historic surface inventories of glacierized areas within the upper Arve catchment were available (1986 and 2003; [55]), the most recent inventory was used for simplicity throughout the entire simulation period, because the change in the glacierized surface area between the inventoried dates represents less than a 1% of the total study surface area.

4.4. Treatment of Forested Area

Since snowpack simulations in forested areas were not configured to account for sub-canopy processes and satellite observations can be significantly biased by the presence of the trees, these areas were masked out in the SCA analysis.

4.5. Time Span and Initialization of the Simulations

As previously described, simulations were run for the period 1989–2015. Starting from an initial vertical temperature profile of the ground layers corresponding to the mean annual temperature, a spin-up simulation for the 1988–1989 snow year (1 August 1988 to 31 July 1989) was repeated iteratively 10 times, to ensure a realistic ground state when launching simulations. This approach has been found to allow for a reasonable initialization for the simulations of the full time period studied.

Glacierized areas were reinitialized at the beginning of each snow season (1 August) to a value of 40-m thickness of ice, if the total ice thickness was lower than this value, which ensured that ice would be present for the entire snow season (from 1 August of one year to 31 July of the next year). In the case where snow was present on top of ice in a glacierized part on the date of reinitialization, additional ice was added below the snow surface, so that the state of the surface would not change but the total ice amount would be adjusted. The six deepest Crocus layers (these that simulate ice evolution) were initialized with a density value of 917 kg/m³ and a temperature of 273.16 K. The thickness of these layers were set to progressively transition from a shallow thickness for the upper ice layer (0.01 m) to thicker layers in the deepest part of the ice (with a 5-fold difference factor between one layer and the one above), resulting in a total ice thickness of 39.06 m. The ice initialization was also performed during the spin-up so that ground layers below the ice covered areas would also reach a reasonable thermodynamic equilibrium.

4.6. Evaluation Strategy

The availability of direct snow and ice observations for mountain areas is limited. Broadly, when the time between observations is short, the spatial extent is limited and oppositely, when large areas are observed, the temporal frequency is low. Consequently, evaluation of the performance of a model in reproducing the snowpack evolution is difficult because of a lack of information. Although we did not evaluate a hydrological model; in this study, the “observation scale” defined by [75] aided the assessment of the representativeness of the available observations. The observation scale is defined by: (i) the spatial/temporal extent (coverage) of a dataset; (ii) the spacing (space and time resolution) between samples; and iii) the integration volume (time) of a sample (also known as support). These three criteria can rarely be optimized simultaneously. Hanzer et al. [54] provided an overview of the various characteristics and complementary features of various methods, which can be used for evaluation of snow/glacier/hydrological simulations in mountainous catchments. In this study we used the following four observation datasets described on Section 3:

• In situ snow depth from Météo-France stations within the simulation domain.
• Snow covered area (SCA) from MODIS images at 250 m resolution, using a dedicated method to address the influence of complex topography on satellite images.
• Seasonal and annual glacier surface mass balance (SMB) for in-situ stakes measurements.
• Glacier equilibrium-line altitude (ELA) from Landsat/SPOT/ASTER.

Based on the radar charts presented by [54], shown in their Figure 4 and Figure 5, the four datasets used in this study cover almost the full radar chart space (“optimal” validation dataset, which would be perfect if it would be completely covered), thus providing almost an optimal evaluation of the simulation performance.

The four datasets allowed performing a multi-criteria, multi-spatial and multi-temporal evaluation of the simulations with all observations available within the study area. However, not all simulations (punctual, semi-distributed, and distributed) were evaluated using all four observation datasets. The punctual snow depth simulations only provided a preliminary evaluation of the simulation setup in terms of reproducing the temporal snowpack evolution, so only punctual snow depth observations were used in the evaluation of this simulation approach. The three other datasets (SCA, and glacier SMB and ELA) were used in evaluating the semi-distributed and distributed simulations, as these datasets had the appropriate spatial and temporal extents needed to assess the performance of these two approaches.

4.6.1. In Situ Snow Depth Evaluation

With this database has been calculated the root mean squared error (RMSE) and the bias of the punctual simulations for the time periods with data available.

4.6.2. Snow Covered Area Evaluation from MODIS Images:

Statistical Framework for the Comparison between MODIS Images and Model Output

The temporal evolution of the snow covered area (SCA) within the study area predicted by each simulation approach (semi-distributed and distributed) was compared to SCA observations in terms of the root mean squared error (RMSE), the mean absolute error (MAE), and R² calculated on the basis of daily values spanning the entire simulation period during which MODIS data are available (14 years). Special care was taken to ensure the statistical significance of the difference in skill between semi-distributed and distributed simulations since there is a high variability of the skill of a snowpack model from one season to another [76,77]. As a result, the skill of a simulation configuration can change depending on the selected years for evaluation. To assess whether the results obtained with distributed and semi-distributed simulations are significantly different in comparison with the inter-annual variability of the model skill, the uncertainty of the scores was quantified by a bootstrap approach [78]. A total of 100 samples from 14 complete years were randomly selected among the 2000–2014 time series of observed and simulated SCA values. Indeed, a stability test (not shown here) showed that results were stable after 100 repetitions. The sampling was applied on an annual basis instead of individual dates to avoid being affected by the high temporal autocorrelation of the skill during the same snow season. From the 100 samples, we computed the standard deviation of each score, considered as a random variable. Thus, the scores samples of the semi-distributed and distributed simulations could be compared by a t-student test.

In addition, in order to better understand and analyze the statistical results, the temporal evolution of the SCA for selected snow seasons was also analyzed to assess the difference between observations and simulations in different time periods within the season. Error metrics obtained on these snow seasons were compared to average values from the bootstrapped sample.

Evaluation of Spatial Similarity

The spatial similarity between the observed and simulated SCA was evaluated for each simulation approach based on two similarity metrics: the Jaccard index (J), and the average symmetric surface distance (ASSD). The spatial similarity must be evaluated using both metrics simultaneously, in order to avoid mishandling the extreme case where one feature is fully included in the other one, even if there is a large discrepancy. Based on the UWS and snow depth thresholds previously selected from the analysis described above, binary maps (snow presence and absence) were generated for all observation and simulation datasets, by design sharing the same grid, and used to perform these evaluations.

The Jaccard index is the ratio of the intersection between the observed (O) and the simulated (S) snow covered area and their union (Equation (1)). The index values range from 0 to 1, with a value of 1 representing a perfect match between the observed and simulated SCA.

$$J=\frac{\left|O{\displaystyle \cap }S\right|}{\left|O{\displaystyle \cup }S\right|}$$

(1)

The ASSD quantifies the distance between the boundaries of the observed and simulated snow covered area. The ASSD is based on the modified directed Hausdroff distance between boundaries [79]; see [42,59] for more details). ASSD values are expressed in meters, and the smaller the distance the better the match between surface boundaries. The Jaccard index and ASSD were calculated for the 2001–2002 to the 2014–2015 snow seasons. To assess the performance of the two simulation approaches for specific periods, the 2006–2007 and 2007–2008 snow seasons (characterized by lower than average snow conditions) and the 2011–2012 and 2012–2013 snow seasons (characterized by higher than average snow conditions) were analyzed for both the accumulation period (January, February, and March; JFM) and the melt period (May, June, and July; MJJ).

4.6.3. Surface Mass Balance Evaluation from In-Situ Stakes

In this study, we directly used SMB seasonal and annual components at 65 locations encompassing different glaciers, which were directly compared to model simulations corresponding to these locations. RMSE, MAE and R² coefficient values were computed for each sub-basin for the winter, summer and annual SMB components. These three error metrics were calculated by computing the difference between the observed and the simulated SMB (difference of the simulated snow water equivalent between consecutive observation dates) for the simulation pixels in which observation stakes are located. Similar to the SCA evaluation, the significance of the differences between the distributed and semi-distributed approaches was assessed using a bootstrap method based on the resampling of the 20 available observation years.

Finally the simulated (distributed and semi-distributed) and observed temporal evolutions of the SMBs were compared for several elevation bands (the average and standard deviation for all locations within each band were calculated). To address the elevational dependence of the SMB, the seasonal evolution of the observed and simulated seasonal and annual SMB were compared for two snow seasons having opposite characteristics (high (2012–2013) and low (2007–2008) levels of snow accumulation) for the Mer de Glace glacier.

4.6.4. Equilibrium Line Altitude Evaluation from Landsat/SPOT/ASTER

The simulated ELA was calculated for the same dates as the satellite acquisitions. Because of the difference in the spatial resolution of the simulation (250 m) and satellite observations (≤30 m), the average elevation and its standard deviations of the ELA were compared.

5. Results

5.1. Punctual Snow Depth

The observed and simulated snow depth evolution for the 2007–2008 and 2012–2013 snow seasons (lower than and higher than average snow conditions, respectively) for the five stations are shown in Figure 4. The snow depth evolution shows the ability of the SAFRAN–Crocus model chain to reproduce the temporal evolution of snow at these observation stations, taking into account their altitude and terrain shadowing masks, based on a meteorological analysis performed at the scale of the entire Mont-Blanc massif.

Some snow accumulation events were underestimated or overestimated in the SAFRAN–Crocus simulations, compared to observations, as illustrated by the discrepancies between the simulated and observed snow depths, including for the Le Tour (overestimation) and La Flégère (underestimation) stations for the 2007–2008 snow season. If these large discrepancies, mainly coming from deviations on the forecasted snow precipitations amounts are neglected (for instance the observed and simulated snow depths are forced to match just after accumulation events), then we can conceive that the snow depth temporal evolution is well reproduced. This can be well visualized for Lognan station or for La Flegere station on 2007/2008.

Table 1. Error statistics (bias and Root Mean Squared Error (RMSE)) between simulated and in situ snow depth observations for the five meteorological stations in the study area for periods for which observations were available. The locations of the stations are shown in Figure 1.

Observatory	RMSE (cm)	Bias[cm]	Period	Num. Obs.
Chamonix	23.3	12.1	1983–2015	6704
Le Tour	29.6	13.0	1985–2015	6323
Nivose Aiguilles Rouges	66.6	49.4	1983–2015	5902
La Flegere	45.0	−19.1	2003–2015	1231
Lognan	20.8	1.9	1994–2015	5964

shows the RMSE and bias errors between observations and simulations at the five stations. There is a high level of variability between the errors for the various stations. It is noteworthy that the number of observations available and the time periods (which could have marked differences on total seasonal snow accumulation) affected the significance of the RMSE and bias for the various stations (Table 1). The RMSE values ranged from 20.8 to 66.6 cm and the bias ranged from −19.1 to 49.4 cm. These values are small relative to the total snowpack thickness (snow depth observations were commonly >200 cm, and in some cases exceeded 300 cm). However, for the Aiguilles Rouges station the RMSE and bias estimates were higher than for the other stations. This may be because this station is exposed to major wind-induced snow transport episodes that were not accounted for in the simulation. In addition to these events, this station is also affected by errors related to the meteorological forcing, such as the large underestimation for the first snowfall in 2007–2008.

5.2. Snow Cover Area Distribution

Table 2. Unmixing_wholesnow (UWS) threshold selection for various snow thicknesses selected as thresholds for the 2008–2009 and 2009–2010 snow seasons for distributed and semi-distributed simulations. Bold values indicate the selected snow depth and snow cover area (SCA) thresholds.

Threshold		Distributed Approach			Semi-Distributed Approach
		R2	RMSE	MAE	R2	RMSE	MAE
SCA [0, 1]	SD (m)
0.25	0.10	0.803	13.84	9.85	0.790	15.48	10.36
	0.15	0.807	13.75	9.54	0.793	15.04	9.79
	0.20	0.806	13.79	9.60	0.789	16.41	12.05
0.35	0.10	0.821	12.64	8.36	0.809	14.31	9.79
	0.15	0.828	12.51	8.24	0.815	13.59	9.60
	0.20	0.815	12.86	8.54	0.811	14.90	10.49
0.45	0.10	0.812	13.47	9.33	0.798	15.29	10.47
	0.15	0.813	13.69	9.58	0.805	14.31	9.81
	0.20	0.813	13.38	9.24	0.80	16.29	11.17

shows the SCA simulation results estimated tested against 0.1, 0.15 and 0.2 m snow depth thresholds compared with the various UWS thresholds tested, for the 2008–2009 and 2009–2010 snow seasons (average snow accumulations) and for the semi-distributed and distributed approaches. It shows that the evaluation metrics are only slightly sensitive to the choice of these thresholds and that for every threshold and metrics the ranking of the two approaches remains the same. In light of the results of the sensitivity tests, we selected a 0.15 m snow depth threshold for the simulations and 0.35 SCA threshold for MODImLab UWS product for classifying a pixel as snow-covered or not.

Figure 5 depicts the spatial distribution of the snow water equivalent (SWE) simulated (with both approaches) for two dates: in the accumulation period (28 February 2003) and in the early melting period (24 April 2003). Figure 5 also shows for both dates the UWS product from MODImLab. The overall SWE spatial patterns and values are similar in both approaches. However, the semi-distributed simulation fails on reproducing the accumulation on certain areas (for instance in low areas of Mer de Glace glacier see location in Figure 1). Some of the discrepancies between the observed SCA and the simulated SWE are related with deviations in the simulations but others also originated on deficiencies of remote sensing observations on complex alpine terrain (highly rugged topography, vegetation and mixes pixels)”.

5.2.1. Snow Covered Area Dynamics

The results of simulation of the SCA in the study area for 5 of the 14 snow seasons allowing a comparison with MODIS data are shown in Figure 6 (left panel). This figure shows that both approaches were able to reproduce the SCA evolution based on MODIS images. In view of dispersion graphs (Figure 6 right panel) the bias for low SCA values is more pronounced for semi-distributed simulations than for distributed simulations. These discrepancies are mainly due to the differences between observations and simulations on the late melting period.

Figure 7 (left panel) shows the SCA evolution for four snow seasons, two having lower than average snow conditions (2006–2007 and 2007–2008 seasons) and two having higher than average snow conditions (2011–2012 and 2012–2013 seasons). In winter the simulation slightly overestimated the SCA compared with observations, but during summer and autumn the simulations underestimated the SCA. However, the distributed simulations reproduced the observed SCA more closely. For all four seasons, the semi-distributed simulations generated larger underestimates of the SCA during summer and early autumn than the distributed approach (Figure 7 right).

Using the terrain aspect classification for semi-distributed simulations, it is possible to evaluate the impact of terrain shadowing effects. From the eight orientation classes we identified two main groups: those having a northern aspect (N, NW, NE) and those having a southern aspect (S, SE, SW). Figure 8 shows the observed and simulated SCA evolution for higher than average and lower than average snow accumulation seasons in relation to these two terrain classes. The variability in the SCA was well captured for the two aspects by both the semi-distributed and distributed simulations. Overall, the simulation underestimated the SCA during late spring and summer in northern aspects. For southern aspects, the simulation of the SCA evolution was poorer during winter.

Error estimates for the SCA simulated for the whole study area, and for north and south aspects (

Table 3. R², mean absolute error (MAE) and RMSE average and standard deviations values from the 100 sample bootstrapping for the observed and simulated SCA (based on the distributed and semi-distributed approaches) for the entire time period with SCA observation (2001–2015). Results for the entire study area and for North and South Expositions are presented. Error metrics in bold note p-values of the T-student test lower than 0.01 (99% confidence interval for rejecting null hypothesis).

Exposition	Approach	R2	MAE	RMSE
Whole catchment	Semi-distributed	0.819 ± 0.022	10.40 ± 0.39	15.2 ± 0.71
	Distributed	0.821 ± 0.021	8.34 ± 0.30	12.6 ± 0.77
North aspect	Semi-distributed	0.721 ± 0.036	10.09 ± 0.52	15.98 ± 0.88
	Distributed	0.726 ± 0.035	7.57 ± 0.38	12.73 ± 0.97
South aspect	Semi-distributed	0.858 ± 0.018	10.17 ± 0.31	14.78 ± 0.64
	Distributed	0.857 ± 0.016	9.83 ± 0.39	13.19 ± 0.70

,

Table 4. RMSE, MAE and R² values for the observed and simulated SCA (based on the distributed and semi-distributed approaches) for 2006–2008 time periods for the whole catchment, Northern aspect (N, NE, NW) and Southern aspect (S, SE, SW).

Period	Approach	R2	MAE	RMSE
Whole catchment	Semi-distributed	0.744	10.756	16.903
	Distributed	0.756	8.74	14.82
Northern aspect	Semi-distributed	0.58	11.26	18.36
	Distributed	0.59	8.61	15.62
Southern aspect	Semi-distributed	0.80	10.17	16.48
	Distributed	0.815	10.34	16.21

and

Table 5. RMSE, MAE and R² values for the observed and simulated SCA (based on the distributed and semi-distributed approaches) for 2011–2013 time period for the whole catchment, Northern aspect (N, NE, NW) and Southern aspect (S, SE, SW).

Period	Approach	R2	MAE	RMSE
Whole catchment	Semi-distributed	0.881	11.56	15.58
	Distributed	0.895	7.99	11.10
Northern aspect	Semi-distributed	0.82	11.30	16.38
	Distributed	0.84	7.79	11.69
Southern aspect	Semi-distributed	0.902	10.98	15.09
	Distributed	0.905	8.25	11.81

), were lower for the distributed simulations than for semi-distributed ones. For instance the average RMSE error for the SCA decreases from 15.2% for the semi-distributed approach to 12.6% for the distributed simulations considering the whole study period. When accumulation period (January, February and March) RMSE is computed, a value of 6.34% is obtained for semi-distributed simulations and 6.28% for distributed ones. In contrast when these values are obtained for the melting period (May, June and July) it is obtained a 21.08% RMSE for the semi-distributed approach and a 15.61% RMSE for the distributed approach. RMSE and MAE standard deviations obtained from the bootstrapping (Table 3) were lower than the difference between the scores obtained for distributed and semi-distributed approaches. The p-values for these two error metrics were lower than 0.01 and thus the null hypothesis was rejected with a 99% confidence interval, demonstrating that the skills of distributed and semi-distributed simulations are not statistically equivalent. Conversely the R² standard deviation of the SCA is high compared to the difference between the scores of the two approaches. As a result, the high p-value indicated (in this case above 0.05) that the null hypothesis should be accepted and that these scores are not statistically different between the two approaches. R², MAE and RMSE average values for snow conditions higher than average (2006–2007 and 2007–2008 snow seasons, Table 4) and lower than average (2011–2012 and 2012–2013 snow seasons, Table 5) also show the better capacity of distributed simulations to reproduce SCA evolution. The t-student test demonstrated that RMSE and MAE results for the approaches are statistically different, and that for all aspects and time periods, the distributed simulations exhibits lower error statistics. We can conclude that the distributed approach significantly better reproduce the SCA evolution.

The differences in the error metrics (RMSE and MAE) between distributed and semi-distributed simulations are significant for both, north and south aspects but higher for north aspect. However, it must be highlighted that for the whole catchment and for any aspect, the null hypothesis can be accepted based on the R² value between distributed and semi-distributed approaches. This means that the added value of the distributed approach is not visible on this criterion.

5.2.2. Evaluation of the Spatial Similarity

The temporal spatial similarity between the observed and simulated SCA is exemplified in the temporal evolution of the Jaccard index and ASSD.

Table 6. Average values of the Jaccard index and average symmetric surface distance (ASSD) values for each simulation approach for various time periods.

Period	Approach	Jaccard	ASSD
Entire period (2001–2015)	Semi-distributed	0.817	0.912
	Distributed	0.832	0.975
2006–2007 to 2007–2008	Semi-distributed	0.783	0.920
	Distributed	0.801	0.952
2011–2012 to 2012–2013	Semi-distributed	0.826	0.897
	Distributed	0.836	0.952

shows the average values for J and ASSD for the entire study period and for the 2006–2007 and 2007–2008 snow seasons (lower than average snow conditions) and the 2011–2012 and 2012–2013 snow seasons (higher than average snow conditions).

The higher scores found during seasons having high levels of snow accumulation were expected because of the larger areas covered by snow. Figure 9 shows the temporal evolution of the Jaccard index and ASSD for high and low level snow accumulation seasons. The difference between the distributed and semi-distributed simulations was almost undetectable for most dates and only during the last part of the melting season (August–September), distributed simulations were found to be perform slightly better (higher J index and lower ASSD). This shows that except for some particular time periods, differences in the spatial similarity with the observed SCA with the two simulation approaches are minor.

Table 7. Average values of the Jaccard index and ASSD for each simulation approach for the maximum (January, February, March (JFM)) and minimum (May, June, July (MJJ)) snow accumulation periods.

Period	Approach	Jaccard Index		ASSD
		JFM	MJJ	JFM	MJJ
2006–2007	Semi-distributed	0.9535	0.802	0.687	1.152
	Distributed	0.9557	0.823	0.704	1.104
2007–2008	Semi-distributed	0.950	0.793	0.717	1.062
	Distributed	0.951	0.809	0.724	1.043
2011–2012	Semi-distributed	0.968	0.756	0.711	0.983
	Distributed	0.967	0.754	0.734	0.994
2012–2013	Semi-distributed	0.980	0.790	0.199	1.271
	Distributed	0.990	0.799	0.198	1.250

shows the average Jaccard and ASSD index values obtained for the JFM and MJJ periods for the four snow seasons analyzed in detail (high and low level snow accumulation seasons). Again, a minor improvement on capturing the spatial patterns in heterogeneous mountain terrain was obtained with distributed snowpack simulations. Not surprisingly, the values in Table 7 also show higher scores for the two simulations approaches during winter and early spring, when the SCA was higher.

5.3. Glacier Surface Mass Balance

Figure 10 and Figure 11 show the simulated and observed temporal evolution of the surface mass balance for the 300-m elevation bands. They show good agreement between observations and simulations with respect to year-to-year SMB variability. During winter the snow accumulation at high elevations was underestimated. For elevations above 2700 m.a.s.l. observations indicate higher positive glacier SMB than the simulations, and the difference between the observed and simulated SMB increased at higher elevations. During summer, when solid precipitation has no or marginal influence in low elevation areas and little influence at higher elevations, the observed and simulated SMB values were similar for elevations above 2100 m.a.s.l. for the Mer de Glace glacier, and above 2400 m.a.s.l. for the Argentière glacier. Nevertheless, in high elevation areas the summer SMB deviation was also underestimated on the simulations.

The combination of the simulated winter SMB and summer SMB produced an annual SMB showing underestimated snow accumulation at high elevations (>3000 m.a.s.l.) and understimated melting at low elevations (2400 m.a.s.l. for the Argentière glacier, and <2100 m.a.s.l. for the Mer de Glace glacier). Thus, the glacier annual SMB included summer and winter variations, which in some cases negated each other. The contrasting performance of the simulations in reproducing the SMB between high and low elevations is clearly illustrated in Figure 12. This shows the altitudinal dependence of the SMB for two snow seasons, one having a lower than average level of snow accumulation and the other a higher than average level. The simulated summer, winter and annual SMB values for the two approaches underestimated the observed values at both low (higher negative loss of water equivalents observed) and high (lower positive loss of water equivalents observed) elevation areas. Nevertheless, the SMB simulations at intermediate elevations correctly reproduced the observed values, and the temporal evolution of the SMB for the 20 years (Figure 10 and Figure 11) was well reproduced by the simulations overall. These results are consistent with the findings of [74] in another glacier of the French Alps using comparable modeling tools.

The performance of simulations in reproducing glacier SMB must take account of the areal extent at differing elevations. Elevations > 3000 m.a.s.l. represent 37% and 52% of the surface areas of the Argentière and Mer de Glace glaciers, respectively. The Argentière glacier has <10% of its surface area below 2400 m.a.s.l., and the Mer de Glace glacier has <7% below 2100 m.a.s.l. These relative extents of glacierized surface area show that for large areas of the glaciers, the SMB was accurately reproduced by the simulations. However, for large parts of the glacierized areas, there were marked differences between the observations and simulations; although the year-to-year evolution was accurately reproduced, this demonstrates the need to improve simulation methods.

In general, the distributed simulation values for the SMB were slightly closer to the observed SMB values than were those from the semi-distributed simulations (in average the RMSE is reduced from 1.475 m of Water Equivalent (WE) for semi-distributed to 1.375 m W.E. for distributed simulations).

Table 8. R², MAE and RMSE average and standard deviations values from the 100 sample bootstrapping for the observed and simulated SMB for Mer de Glace (Mdg) and Argentière (Arg) glaciers (based on the distributed and semi-distributed approaches. Error metrics in bold note p-values of the T-student test lower than 0.01 (99% confidence interval for rejecting null hypothesis).

Glacier	Period	Approach	RMSE	MAE	R2
Arg	WSMB	Semi-distributed	0.56 ± 0.027	0.43 ± 0.022	0.54 ± 0.065
		Distributed	0.51 ± 0.028	0.42 ± 0.023	0.50 ± 0.073
	SSMB	Semi-distributed	0.96 ± 0.057	0.78 ± 0.045	0.75 ± 0.031
		Distributed	0.77 ± 0.049*	0.62 ± 0.047	0.84 ± 0.019
	ASMB	Semi-distributed	1.21 ± 0.059	0.99 ± 0.055	0.72 ± 0.021
		Distributed	1.18 ± 0.062	0.909 ± 0.054	0.71 ± 0.055
Mdg	WSMB	Semi-distributed	0.73 ± 0.031	0.57 ± 0.024	0.64 ± 0.041
		Distributed	0.76 ± 0.026	0.58 ± 0.027	0.59 ± 0.045
	SSMB	Semi-distributed	1.47 ± 0.093	1.18 ± 0.083	0.746 ± 0.049
		Distributed	1.19 ± 0.069	0.86 ± 0.057	0.86 ± 0.014
	ASMB	Semi-distributed	1.74 ± 0.095	1.36 ± 0.075	0.76 ± 0.041
		Distributed	1.57 ± 0.088	1.16 ± 0.069	0.838 ± 0.020

shows RMSE, MAE and R² means and standard deviations obtained from the 100-member bootstrap sample (a stability test, not shown, showed that stable results were attained with this sample size). For most of the error metrics, the standard deviations are lower than score differences and the p-values are low enough to reject the null hypothesis. This shows that results obtained with the two simulation approaches are statistically different. In winter, the SMB simulations show similar results. For both glaciers, lower RMSE and MAE are obtained for distributed simulations and better R² for semi-distributed simulations. In contrast, during summer all scores show better results when the distributed approach is used. The annual SMB also exhibit better results for distributed simulations.

5.4. Glacier Equilibrium Line Altitude

The temporal evolution of the ELA for the five largest glaciers in the study area is shown in Figure 13. Despite differences in the spatial resolutions of simulations and observations of ELA, simulations were able to capture changes in ELA during the 26 years of the study. For most of the years and glaciers simulated, ELA values derived from the distributed approach were closer to those observed. However, for certain years, better results were obtained with semi-distributed simulations.

Table 9. Average differences, standard deviations, slope of the linear adjustment, and R² values for the observed and simulated ELA five glaciers of the study area.

Glacier	Approach	Avg Dif (m)	Std. Dev (Differences) (m)	Slope	R2
Mer de Glace	Semi-distributed	155.11	69.62	0.715	0.420
	Distributed	88.57	48.90	0.869	0.627
Leschaux	Semi-distributed	158.34	101.84	0.188	0.102
	Distributed	110.73	109.67	0.560	0.586
Talèfre	Semi-distributed	105.14	59.25	0.4936	0.2336
	Distributed	80.12	41.87	0.766	0.476
Le Tour	Semi-distributed	105.14	59.25	0.339	0.528
	Distributed	84.33	68.71	0.625	0.715
Argentière	Semi-distributed	63.89	42.87	0.270	0.103
	Distributed	54.52	31.85	0.578	0.381

shows the average absolute differences between observations and simulations and the linear adjustments for the five glaciers. These results show a systematic positive bias on the simulated ELA which is consistent with the underestimation of the summer SMB revealed by the results introduced previously.

6. Discussion

6.1. Overview of SAFRAN–Crocus Performance

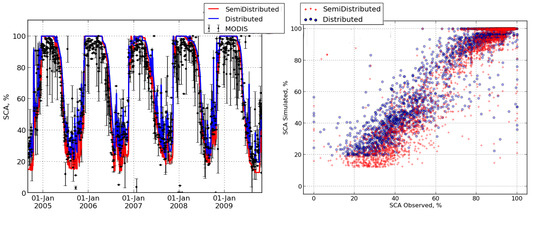
The observation dataset used in this study enabled a multi-criteria spatio-temporal evaluation of the performance of snowpack simulations at the scale of a large alpine catchment, featuring a complex topography and significant glacier coverage (32%). These analyses were accomplished using the operational, semi-distributed version of SAFRAN–Crocus. This may constitute the most exhaustive evaluation of this model chain over a large mountain area for a long time period. The analysis of the results of semi-distributed and distributed simulations provided, in addition, a holistic evaluation of the snow and ice dynamics in the study area. Overall, the SAFRAN–Crocus simulations have shown a good capability for reproducing the temporal evolution and spatial variability of snow and ice during the study period.

The simulations were evaluated using snow depth data from five Météo-France stations. Their ability to reproduce a bulk variable such as snow depth suggests that the main simulation processes were satisfactory, especially those related to the various components of the energy and mass balance. These findings are consistent with previous evaluations of the SAFRAN–Crocus system [36,70]. Crocus simulates the energy and mass exchanges with soil and atmosphere and also within the snowpack layers in 1D, but it does not intrinsically simulate small scale topographic effects on snow depth distribution in 2D and beyond, such as preferential deposition, wind-induced snow drift and snow avalanches [29]. The goal of the present study was to assess specifically the added-value of accounting for topography-driven radiative effects (topographical shadowing), which the distributed approach allows, in contrast to the semi-distributed approach. Further studies will explore in more detail how more sophisticated model approaches could further improve the performance of distributed simulations, which is deliberately beyond the scope of the present study [31,80,81].

Distributed information on the snowpack evolution from the MODIS sensor enabled evaluation of the simulation results on a suitable temporal scale. Although many MODIS images were discarded because of cloud cover, they demonstrated the capacity of SAFRAN–Crocus to simulate the spatial distribution of the SCA over time for large areas having high spatial heterogeneity. The 14-year time period spanned is longer than in all the previous similar evaluations of this model choice, and at a higher spatial resolution [42]. The evaluation of the spatial similarity between simulations and observations (Jaccard index and ASSD) showed that the SCA spatial pattern was well reproduced. The simulated SCA for winter was in close agreement with observations, as most of the study area was covered by snow. In contrast, during summer the performance of simulations declined, as evidenced by the increase in ASSD and the decrease in the Jaccard index. As small scale topographic effects, that control snow accumulation on preferential accumulation areas, were not included in the simulations, deviations from observations could have increased for certain periods, particularly the late melt period. These processes, which are mainly driven by small topographic features, can be long-lasting during the late melt period [29,82]. This was particularity evident in comparisons of the scores for the 2006–2007 and 2007–2008 periods (lower than average snow conditions) with those for the 2011–2012 and 2012–2013 periods (higher than average snow conditions) (Table 3). The differences in response may have originated from the higher weight of glacier melt processes in years with shallower than average snow depth. For these years, the good capability of the model on reproducing snow melting is lumped because the snow distribution is not appropriately simulated.

The availability of observations of the glacier SMB over a long time period provided an opportunity to evaluate the performance of the simulations in capturing the snow and ice temporal evolution over a wide range of elevations over glacierized areas. Contrasting simulation performances were found in the various elevation bands, and changed with the time period involved (summer, winter, or annual scales). The performances in simulating the SMB for the Argentière and Mer de Glace glaciers differed at high and low elevations. Although the observed SMB was always higher than the simulated one for elevations exceeding 2700 m, the opposite was observed for areas having elevations below 2100–2400 m. As the temporal variability of solid precipitation generally explains the temporal variability of the winter SMB [12], it is important to consider differences between simulated and observed solid precipitation, and how these could affect underestimation of the SMB in simulations. Studies in the same study area and nearby glaciers suggest that at high elevations the SAFRAN reanalysis may underestimate solid precipitation at ratios ranging from 1:1.2 at 2000 m.a.s.l. and 1:2.0 at 3200 m.a.s.l., with an average of 1:1.5 at the glacier scale [12,56,72,74]. This mainly results from the lack of precipitation observations at high elevations available for assimilation into the SAFRAN reanalysis; consequently divergences increase with elevation. Despite this shortcoming, the simulations captured the inter-annual fluctuation of the winter SMB for all elevation bands. During summer, SMB is mainly driven by temperature variations in the two glaciers [12], thus simulations results are closer to observations, particularly at higher elevations. In summer, most precipitation is liquid, and so has a lower impact on the energy balance of the glaciers [83]; this may explain the improvement in summer simulations for most elevations.

For the entire study period the SAFRAN–Crocus simulations effectively reproduced the observed inter-annual evolution of the study area glacier ELA. However, some differences were evidenced, particularly on steeper glaciers, because the high spatial heterogeneity was not well captured by the simulations. For mid-latitude mountain glaciers, the annual evolution of the ELA can be considered to be a good proxy for the glacier surface mass balance [66]. Thus, observations of the glacier SMB, together with the ELA, provide for a complete evaluation of glacier temporal evolution.

6.2. Distributed vs. Semi-Distributed Approaches

In this study we performed distributed and semi-distributed snowpack simulations using the same, originally semi-distributed, meteorological forcing (SAFRAN), the same snowpack model (Crocus), and the same evaluation setup. Thus, the two approaches were affected by the same methodological limitations, and differences in performance can directly be traced to differences in the approaches themselves. The simulation results were consistent with the observed SCA evolution using the two approaches. However, better results were obtained from the distributed simulations during late summer. Similarly, an improvement on simulation results was obtained with distributed simulations. This is probably due to the fact that the energy balance is more accurately simulated in the distributed approach, as it accounts for terrain shadowing effects on incoming solar radiation. Therefore, for aspects and/or time periods for which the differences on simulation of the incoming solar radiation have a critical weight, differences on snowpack simulation between the two approaches are more pronounced.

Based on the glacier SMB scores and their temporal evolution, it was found that the ranking of the simulation approach could be different depending on the season. The winter SMB evaluation showed similar results for the two methods. In contrast, the distributed approach was better at simulating the summer SMB. The distributed approach exhibited better skill at the annual scale.

The distributed simulation of the ELA generally showed closest agreement with observations, but not for every year. This may be related to the coarse pixel size, which did not enable to capture the effects of the high spatial heterogeneity of the terrain. The annual ELA covers a small area of the glaciers (it represents the snow line limit between snow-free and snow-covered areas), and thus the effect of spatial heterogeneity is likely to be significant.

Overall, the distributed simulations were slightly better at reproducing observational data during the whole study period. For SCA and SMB, the improvements described above are significant according to the bootstrap results analysis. However, it should be noticed that the bootstrap method applied here only compares the difference of skill between two simulations with the inter-annual variability of the scores. In addition it has been shown how, that for particular dates and/or specific time periods, semi-distributed simulations do not appropriately reproduce snowpack distribution, since are not able to take into account the influence of terrain shadowing. This is particularly evident during melting period. This way, the SCA spatial distribution and the SMB seasonal and inter-annual evolution obtained with distributed simulations is closer to reality at the end of the snow season than semi-distributed simulations, from which we can expect a superior performance of distributed simulations on reproducing SWE. Despite no observation database was available to evaluate the SWE distribution over the whole study area, the (potential) better capacity of distributed simulations is very-likely to be non-negligible regarding hydrological issues such as streamflow evolution.

Nevertheless, the differences involved by the spatial discretization (distributed vs semi-distributed) can still be lower than other sources of uncertainties common to the two approaches. For example, the two simulations are performed with the same snowpack model and share the same errors in the physical parameterizations of various processes (liquid water percolation, compaction, metamorphism, turbulent surface fluxes, etc.) and the same missing physical processes (e.g., snow redistribution by the wind). Furthermore, the two simulations are forced with the same meteorological reanalysis and share the same meteorological errors. Ensemble simulations based on multiphysics modelling systems [77] and on ensemble meteorological forcings [84], applied to the two approaches, could be performed (with much higher numerical costs) to investigate the significance of the impact of these approaches compared to these uncertainties. Although this is beyond the scope of this work, the significance of the improvements obtained with the distributed discretization should be considered depending on the magnitude of simulations errors resulting from meteorological and snowpack model errors [33,76,85].

Furthermore, depending on the purpose of the simulations and the accuracy required, other factors must be considered. The total CPU time for simulating one complete snow season with the distributed approach is 20 h for a domain of about 10,000 grid cells. Therefore, running several years, several experiments, or larger domains generally require parallel computing resources to improve the real execution time compared to the CPU time. When sufficient resources are available, the superior results of distributed simulations encourage this choice. In the contrary, semi-distributed simulations have lower computing resource requirements, on the order of a factor 100 for this study (about 0.2 CPU hours). A good example of an application in which the computational requirements have a determinant weight are ensemble simulations for projections in several climate scenarios (e.g., [86]), which can be expensive to run and analyze in a distributed configuration, without a substantial added value.

6.3. Limitations of the Satellite Evaluation Datasets

Data on the spatial extent of SCA derived from MODIS images enabled distributed evaluation of the simulations. However, its usefulness in analysis of the performance of spatial simulations is limited, as it does not provide information on other snowpack variables, and imposes restrictions on the spatial resolution. Satellite observations also involve uncertainty, depending on the routines applied for generating the final product and the thresholds used to decide whether a pixel area as covered by snow. After a sensibility test we adopted a 0.35 UWS threshold for considering a pixel as snow covered in satellite imagery [50,61]. We also performed an analysis to select the simulated snow depth threshold for considering a pixel to be snow covered. The 0.15 m threshold selected is consistent with values reported in previous studies [42,52]. Despite mountain areas having a high spatial heterogeneity which also affects snowpack distribution, these thresholds enabled a binary representation of snow presence/absence which finally ensured a consistent SCA evaluation of both simulation approaches.

Such binary classification is a well-established snowpack variable to evaluate its temporal evolution over extended areas [52]. However further investigations analysing in detail fractional snow cover [87,88], compared to simulated snowpack, which at the moment produce constant snow for each pixel; would allow the evaluation of higher spatial resolution snowpack simulations. This is not possible with the binary classification performed in this work.

In addition to the above issues, satellite products can have errors for specific dates. For a small number of days during the study period the SCA obtained from MODIS images did not describe the real extent of snow cover. For these days the SCA did not match the temporal SCA evolution observed on previous and later dates. Furthermore, days having the maximum cloud cover allowed in our analysis could have ±20% SCA variability. This induces uncertainty in the observation for certain dates which can be greater than this of the pixel classification as snow covered in the simulations (note the ±0.05 m snow depths threshold tested). In addition, pixels classified as snow covered in which bare soil may have a non-negligible extension (pixels close to the 0.35 UWS threshold) could introduce discrepancies between observations and simulations, mainly during summer.

Some issues were also evident in evaluation of the ELA. For the smallest glaciers, a reduced number of pixels having the 250-m pixel resolution were considered. As the ELA observations were based on Landsat, SPOT and ASTER satellite images (2.5–30 m resolution) the spatial variability of the simulation made it difficult to identify the glacier margins. The combination of problems in delimitating glacierized areas over smaller ice bodies, and the smooth topography characterizing the simulations compared with real terrain, could cause simulation errors for smaller glaciers.

6.4. Future Perspectives on Distributed Snowpack Simulations

Simulating the snowpack evolution in mountain areas is challenging and will remain so for the decades to come. Although advances in meteorological/snowpack models and simulation approaches are improving the prediction of observational data, inaccuracies remain. Many studies have highlighted the potential to improve snowpack modeling by assimilating observational data [46,89]. Satellite data enables the distribution of the snowpack over large areas to be determined, and the assimilation of such data into snowpack models has been shown to significantly improve the simulation results in theory [44]. In distributed snowpack simulations, almost direct satellite data can be assimilated, in contrast to the semi-distributed approach which needs aggregation methods to enable satellite data assimilation, thereby losing part of the information in this process. Additionally, meteorological forcing models featuring higher spatial resolution are improving simulations of the spatial pattern of meteorological variables in mountain areas [43,90,91]. This will improve snowpack simulations [42,92]; even though it is challenging to combine high resolution numerical weather prediction models with precipitation measurements assimilation in analysis systems. Interest in distributed snowpack simulations will be enhanced when reliable high spatial resolution meteorological forcing data are available, as only this simulation approach can take full advantage of such data.

Further research is needed on parameterizing small scale snowpack processes for incorporation in modeling, including wind driven snow transport [93,94], avalanche snow redistribution [47], and topographic control on snow distribution [29]. Inclusion of these processes, together with the incorporation of reliable meteorological forcing and satellite data, assimilation will improve the accuracy of snowpack simulations over extensive mountain areas.

7. Conclusions

This study provided a detailed assessment of the ability of the SAFRAN–Crocus system to simulate the snow and ice dynamics in complex alpine terrain using distributed and semi-distributed simulation approaches. The study was undertaken in the upper Arve catchment in the western French Alps, with simulations run for the 1989–1990 to the 2014–2015 snow seasons.

The simulations were evaluated based on observations of snow depth derived from five meteorological stations within the study area. This was only performed using punctual snowpack simulations, in order to provide an assessment of model performance over glacier-free terrain. Despite some discrepancies between observations and simulations, the model reliably reproduced the snow depth time series, especially during melt periods.

In regard to the spatial scale of snowpack simulations over extended areas, the semi-distributed and distributed simulations were compared using the same observation datasets, including: (i) the temporal evolution of the snow-covered area based on data from the MODIS sensor, specifically processed to address the impact of complex topography on satellite observation; (ii) measurements of surface mass balance of glaciers within the upper Arve catchment; and (iii) observational data on the annual evolution of the equilibrium-line altitude for the various glaciers considered based on high resolution satellite imagery. Detailed treatment of the effects of complex terrain on the satellite signal such as the one implemented in MODImLab enables an accurate evaluation of the snowpack simulations. Such satellite products are especially useful for assessing in detail the impact of including complex terrain induced shading in the snowpack simulations.

The two simulation methods reproduced quite accurately, and with similar skill, the evolution of the SCA during accumulation events, which was expected because they relied on the same meteorological forcing data. From the winter to early spring period, when the study area is almost completely covered by snow, there was little difference between the two approaches. However, for the melting period the distributed simulations better reproduced the observations.

The simulations for low elevations and elevations > 2700 m.a.s.l. underestimated (negative underestimation in low elevations and positive in high) the observed glacier SMB. Nevertheless, the results of the two simulations were in close agreement with observations at mid-elevation areas, and adequately reproduced the observed annual glacier SMB at all elevations. Overall, the distributed simulations yielded slightly better results.

Based on comparison with ELA data obtained from various satellites at the end of summer, the SAFRAN–Crocus accurately reproduced the inter-annual variability of the snowpack over glacierized areas. However, differences between observations and simulations were shown, particularly for the smallest glacierized areas, where the spatial resolution of the simulations did not enable the high spatial variability of the topography to be included.

Overall, the results of this study demonstrated that distributed simulations reproduce slightly better (but statistically significantly) snowpack dynamics in the alpine terrain of our study area during the whole study period. Distributed simulations take into account the specific topographic characteristics of each pixel (local values of aspect, slope and elevation) and more importantly the effects of terrain shadowing by surrounding areas. Accounting for these two effects over long time periods led to statistically significant better results for the distributed approach. However, the lower computational requirements of semi-distributed simulations together with the flexibility on the design and application scale of the simulation; makes this approach suitable to simulate snowpack evolution for applications that do not require the highest simulation performance and in which the interpretation of results allows higher uncertainties. The intrinsic added value of distributed simulations in our case is limited over the semi-distributed approach when regarding global values but it is better able to reproduce snowpack distribution over complex terrain, leading to improved results on simulating snow spatial distribution. Moreover the methodological framework introduced here paves the way for future assessments of the performance of more sophisticated method, using spatially distributed meteorological forcing and/or relying on satellite data assimilation to improve model predictions during the course of the snow season.