1. Background
Capabilities for spatial measurements of ocean surface turbulence are highly desirable for a wide variety of needs ranging from basic studies of upper ocean mixing processes to data assimilation into high-resolution coastal and ocean circulation models. On the global scale, presently available observations of the ocean currents are provided by satellite altimeters, which are limited to mesoscales and resolve only the geostrophic component of the surface current. Much anticipated launches of the Surface Water and Ocean Topography (SWOT) and Coastal and Ocean measurement Mission with Precise and Innovative Radar Altimeter (COMPIRA) satellite missions will provide some submesoscale altimetry coverage; however, many smaller scale processes, such as non-geostrophic submesoscale turbulence, frontal instabilities, or Langmuir circulations will remain unresolved. Some of these processes are unresolved even by the dense horizontal resolution of surface currents from shore-based high frequency (HF) radars. In situ observations from research vessels or bottom-mounted Acoustic Current Doppler Profilers (ADCP), on the other hand, are essentially Eulerian point measurements, while surface drifters each provide single Lagrangian trajectory. This leaves a wide range of spatial scales from meters to tens of kilometers largely unresolved in the field, leaving hydrodynamic processes taking place on these scales unknown. The hypothesis pursued in this study is that this range of scales can potentially be resolved with an airborne imaging approach.
Generally, airborne ocean remote sensing can employ any band of the electromagnetic spectrum with either sun reflection, passive radiation, or reflection of an actively emitted signal, serving as a source of the measured signal. The need to interpret and relate measured signal in terms of the upper ocean hydrodynamics; however, significantly narrows down available options. Furthermore, even if an obtained image clearly contains some information about the surface turbulence, establishing a quantitative relationship to usable oceanographic variables is always a challenge. Following is a brief overview of some known techniques in visible, infrared, and microwave bands of the spectrum.
1.1. Visible Light Methods
Away from the coast, the small-scale variability of a signal measured by a common airborne visible band image of the ocean surface is mostly due to specular reflections of the sunlight from various facets of surface waves. While repeated attempts to recover wave amplitude spectrum from such imagery have been mostly unsuccessful, it is certainly possible to detect wave phases as they move across an image. With enough dwell time and spatial resolution over each scene, empirical reconstruction of the surface gravity wave dispersion relationship curve is possible, which relates wave number
k to wave frequency
ω. A deviation of this
k-
ω curve from a well-known linear theoretical solution indicates a Doppler shift due to an underlying surface current, which is then calculated iteratively. This can be done from a manned fixed wing aircraft [
1] or from a hovering drone [
2]. Moreover, Doppler shift’s dependence on wavelength can be further exploited to estimate vertical profile of the horizontal current in case of deep water waves [
3], as well as bathymetry in case of shoaling waves [
4].
In higher winds, another prominent feature in visible imagery of the ocean surface is whitecaps. The whitecap coverage fraction obtained from such imagery routinely serves as a basis for parameterizations of a variety of air-sea exchange processes, including the turbulent dissipation rate in the upper ocean [
5]. Additionally, visible imagery often reveals the tendency for surface foam and bubbles to congregate in long streaks or windrows. This behavior becomes especially clear in case the water is surfactant rich, which delays film rupture and thus allows for accumulation of large amount of surface bubbles. These streaks highlighted by bubbles, surface foam, or other drifting material (oil, seaweed, etc.) are often attributed to surface convergence zones between pairs of counter-rotating Langmuir cells [
6].
Sometimes, more commonly near shore, ocean color imagery can detect the fine structure of turbulent flow fields. Sediment, phytoplankton, and colored dissolved organic matter can all act as passive tracers on short time scales, particularly in coastal and inland waters where disparate water masses interact. Consecutive images of a flow rich with tracer features can be used to infer surface velocities by means of pattern tracking velocimetry, e.g., [
7]. However, offshore, smaller gradients in these parameters make them less reliable as tracers for turbulence studies. This limitation can be circumnavigated by creating an artificial ocean color signal by means of water-tracing dye injection. The initial shape and timing of a dye plume released from the shore or from a boat can be designed to highlight turbulent features of interest. The spatial and temporal evolution of the plume’s shape can be captured by an aerial survey and used to infer the properties of the underlying turbulent flow, e.g., [
8]. In addition to the passive imagery capturing horizontal structure of the dye plume, active visible sensing can be useful for resolving the vertical structure of the plume [
9]. This is accomplished by means of a Light Detection and Ranging (LIDAR) method, which directs a short laser beam pulse at the scene, and then splits the returned signal by time of arrival, which is then related to water depth.
1.2. Infrared Methods
Mid- and long-wave infrared (electromagnetic wavelengths ranging from 3 to 14 µm) imagery was found to be an effective remote sensing tool, capable of visualizing upper ocean hydrodynamics with unparalleled detail. A growing number of airborne studies [
10,
11,
12,
13,
14,
15,
16] demonstrated the power of this remote sensing modality to detect and image a wide variety of dynamical processes taking place at or below the air-sea interface. A mid- or long-wave infrared camera is capturing passive radiation emitted by the water no deeper than the skin layer, i.e., tens of microns. However, depending on the surface weather conditions and more specifically the net air-sea heat flux, the vertical thermal gradient across the skin layer can be very large, on the order of Δ
T ≈ 1 °C/mm. Therefore, even slightest distortions of the skin layer by underlying turbulent motions modulate surface skin temperature enough for an infrared camera to detect a surface thermal signature corresponding to the underlying turbulent structure. This is typically expressed by colder temperatures over the surface convergence and downwelling regions, where the thermal skin layer had the longest time to develop, contrasted by warm upwelling and divergence regions.
While such infrared images allow for, arguably, the most detailed visualization of the surface turbulence, inferring usable oceanographic parameters from them remains a challenge. Strictly speaking, one must start by solving the heat budget equation (see [
17,
18]), which involves in situ measurements of heat flux boundary conditions, and then face the directional ambiguity of converting a scalar gradient into a surface velocity vector field. A more feasible quantitative method for analyzing infrared imagery involves turbulent length scale analysis, which can lead to useful quantities such as the depth of the flow and its dissipation rate [
19,
20]. Furthermore, an even more straightforward use of feature-rich infrared imagery is by treating it as a passive tracer and applying Pattern Tracking Velocimetry principles, i.e., tracking image deformations to infer velocity vectors. This approach often results in high-resolution surface velocity vector maps [
15,
21,
22]. One concern regarding this method, however, is that the surface temperature is not strictly conservative, so it is not an ideal passive tracer. This limitation might introduce low velocity bias, especially on the smallest resolved scales.
Lastly, airborne infrared imaging methods, and particularly their sensitivity to subsurface turbulent currents, have found a place in more practical real-time applications, providing an effective underwater moving target detection tool. Even in purely scientific field deployments, infrared cameras are sometimes used to first find a feature of interest, such as an underwater mount or a submesoscale eddy, and then guide slower in-water assets for a more detailed and quantitative investigation [
23].
1.3. Microwave Methods
A well-known feature of a common marine radar is its ability to detect signatures of large surface waves propagating through the field of view. This is due to the backscatter power dependence on local incidence angle and wave shadowing effects, combined with the radar’s sensitivity to surface waves with lengths commensurate with the radio frequency wavelength (i.e., gravity-capillary waves with wavelengths on the order of a few cm in the typical case of an X-band marine radar), which are intensified while riding on crests of dominant waves. This ability to sense roughened ocean surface is the underlying principle for a variety of active microwave sensors used to infer ocean surface currents. In many respects, these algorithms rely on the same
k-
ω principles, as the visible methods described in
Section 1.1. The ability to track the propagation of wave phases across the field of view allows for the reconstruction of the dispersion relationship curve. The Doppler shift of the curve is then used to infer the value of the underlying current [
24]. Similarly, on a larger scale, shore-based HF radars broadcast low power radio frequencies seaward, and use Doppler shift distortions of the returned signal to infer radial component of surface currents with up to 200 km range. To triangulate the full current vector, a spatial array of such radars is positioned along the shoreline, providing continuous coverage by at least two radars along the coastal waters, thus delivering an essential coastal current monitoring resource [
25].
The major departure of microwave methods from visible and infrared imaging is in the way an image is constructed. For a ground- or ship-based radar, the azimuthal angle resolution comes either from the rotation of a directional antenna, or by means of phase detection using a phased array antenna, whereas the range resolution comes from the time delay of the returned signal in conjunction with its RF bandwidth. Because of this fundamental difference, the range resolution does not deteriorate with range, but is only limited by the strength of the returned signal. The low grazing angle active microwave remote sensing techniques, which utilize Doppler shift measurements, are subject to the wave shadowing bias, where most of the signal comes from wave crest reflections. This effect is corrected for by assuming a standard shape of the wave field; however, this correction can be a source of uncertainty and particularly makes the task of inferring wave amplitude information prone to error. At the same time, wave shadowing is beneficial and acts to boost the useful signal in more conventional methods, which rely on backscatter power measurements.
Airborne (and spaceborne) radars used for ocean surface sensing rely on similar principles with the addition of utilizing the platform motion. In the case of Synthetic Aperture Radar (SAR), the motion is used to synthesize a long antenna by coherently combining data collected as the aircraft flies past the scene. This long antenna then provides fine azimuthal resolution, while also allowing for multi-angle looks of the scene as the aircraft passes by. The mobility of an airborne SAR gives it the obvious advantage of on-demand deployment over the areas of interest. The altitude of the platform allows discarding low grazing angles and thus avoiding the wave shadowing limitation. Several antenna configurations and sampling principles have been employed over the past three decades, ranging from the first demonstration of along-track interferometric (ATI) SAR [
26], to the first spaceborne mission TerraSAR-X launched in 2007. The possibility of full current vector retrieval using dual-beam ATI SAR was demonstrated by [
27,
28], and directional wave spectrum retrieval by [
29].
1.4. Common Challenges and Trade-Offs
In the planning stages of an airborne experiment, it is easy to overlook some of the more obvious elements of an airborne setup and sampling strategy, which can be detrimental to the quality of the final product. First, the various environmental conditions, and more specifically atmospheric conditions can play a significant role in the quality of airborne data. Visible and infrared sensors are most susceptible to signal contamination by the atmospheric contribution, which is weak at low altitudes, but grows cumulatively with the atmospheric path length, especially if water vapor and aerosol concentrations are high. For high altitude flights and spaceborne sensors the separation between various oceanic and atmospheric contributions to the signal is done with dedicated radiative transfer models. Additionally, the presence of clouds often presents a problem, either as a direct viewing obstacle, or as a source of irregularities in the amount of downwelling radiation, which is reflected from the water surface and then measured by the sensor. In this regard, microwave radiation’s ability to penetrate clouds makes microwave remote sensing methods far more robust, only limited by the presence of precipitation. On the other hand, microwave methods rely on the presence of surface roughness, which imposes an additional requirement for at least moderate wind conditions. High winds, however, present a new challenge for all types of remote sensing, primarily in the form of breaking waves. Typically, they represent the strongest part of the signal in any band, and unless they are the subject of the experiment, inaccuracies of their removal can make a large contribution to the uncertainty of the underlying measurement, such as ocean surface current retrieval.
Second, both visible and infrared images are susceptible to sunglint contamination. The variability of the surface wave slope provides frequent opportunity for a direct sunbeam reflection into the camera’s field of view, thus saturating some and sometimes most pixels within an image. The best way to avoid this issue within an infrared image is nighttime flights, which coincidentally are also favorable due to the typical cooling of the ocean at night. The upward air-sea heat flux tends to make upper ocean unstable and more susceptible to overturning motions, which in turn result in feature-rich infrared imagery. However, passive visible light remote sensing relies on the sunlight for the source of signal. Therefore, during the day both visible and infrared sensors must be oriented such that the incidence and the azimuthal angles of the cameras do not overlap with the range of sunglint reflection angles. Another related requirement imposed by visible and infrared cameras is that their incidence angles should be close to nadir, and away from low grazing angles. This is because surface reflections begin to dominate over emissions at low angles, and the atmospheric path length becomes long and can pick up noticeable atmospheric contamination. Combined, these limitations result in the optimal data collected with nadir looking cameras, aircraft tracks either towards or against the sun, and during the time of intermediate solar elevation angles. Overcast conditions eliminate limitations associated with sunglint, but can introduce other issues in the form of limiting maximum unobstructed altitude, as well as more likely precipitation. Another method to mitigate sunglint is with a polarization filter, but that does not solve the problem completely and comes at a price of signal strength reduction.
Third, while a manned fixed wing aircraft remains the airborne platform of choice in most cases, numerous experiments employed helicopters, blimps, aerostats, helikites, and most recently unmanned aerial systems (UAS) or drones. The primary motivation for the use of alternative platforms is typically cost reduction, but also mitigation of low altitude flight safety concerns and the ability to hover and collect long time series over a scene. Recent rapid development of UAS technology combined with miniaturization of hyperspectral visible to near infrared imagers, LIDARs, as well as infrared cameras, made the entry level of these remote sensing modalities feasible for a wide range of new applications, including coastal oceanography.
Lastly, the validation of remotely sensed ocean surface currents remains a significant challenge. The lack of a reliable source of validation data is due to the unique ability of remote sensing methods to obtain large spatial coverages, unparalleled by more traditional in situ velocity measurement methods. Nonetheless, the two types of measurements used for the validation purpose are ADCPs and surface drifters. However, in addition to the inadequate spatial coverage, another significant issue is the apparent mismatch between reference depths of remote and in situ current measurements. Neither a down looking ship mounted ADCP, nor the up looking bottom-mounted (or mooring suspended) ADCP resolves the top several meters of the water column. Meanwhile, vertical gradients of the horizontal current near the surface can be very large, making drifters of a particular design preferential to following currents at a particular depth, e.g., [
30]. The vertical structure of the currents in the upper ocean is highly complex and difficult to model, yet its knowledge is necessary to evaluate the differences in current measurements at varying depths. This, in turn, emphasizes the need to specify the reference depth of a current measurement provided by a given remote sensing technique. This estimate is often overlooked, yet can be widely different from one remote sensing technique to another, which is expected to strongly affect the values of retrieved currents.
1.5. Objectives of This Study
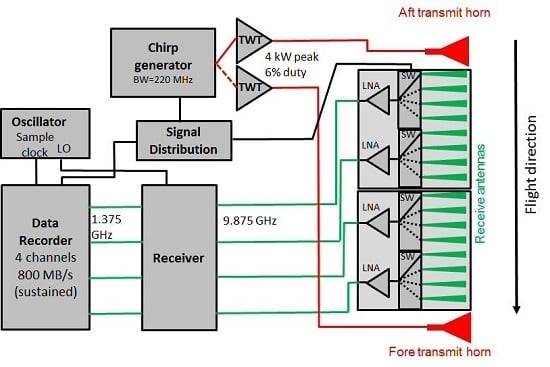
The objective of this study is to evaluate the ability of the airborne remote sensing to accurately measure ocean surface currents on spatial scales of 10 s to 1000 s of meters. For this purpose, the experiment described in this paper simultaneously employs some of the above-mentioned methodologies of ocean surface current retrieval, more specifically: (1) hyperspectral visible-near infrared (VNIR) imaging of fluorescent dye releases; (2) mid-wave infrared (MWIR) imaging of sea surface temperature modulations by subsurface turbulence; and (3) active microwave surface imaging with a Multichannel Synthetic Aperture Radar (MSAR). The study deals with many of the common challenges listed above, including an attempt to compare and validate against a bottom-mounted ADCP, as well as cross-comparison among various remote sensing products. The focus of the paper is on the technical details of the experimental setup and processing algorithms, which are given in
Section 2. The resulting quantitative measurements of ocean currents obtained by the aircraft are presented, intercompared, and validated against ADCP in
Section 3, followed by a discussion of the results, limits of their applicability, and associated uncertainties in
Section 4.
4. Discussion
Each of the airborne remote sensing modalities demonstrated above was able to deliver a unique and valuable perspective on the structure and intensity of ocean surface currents along aircraft’s swaths. Here we present an evaluation and discussion of these results in their own right, but more importantly attempt to inter-compare them to expose important differences between various remote sensing techniques and validate retrieved velocities against in situ ADCP measurements. Two primary quantitative metrics used for these purposes across the paper are standard deviation of velocities, equally band passed over a range of length scales, and velocity power spectra. The slope of the power law that the spectra tend to follow is considered, as well as its absolute value.
The smallest velocity scale resolved by the dye plume velocimetry has been estimated at around 100–200 m, or approximately 10 times the mixed layer depth (see
Section 2.3.3 and
Section 2.3.4). However, little attention has been given by the boundary layer turbulence community, nor by this paper so far, to the importance of the largest resolved length scale. The variability of velocity along plumes (
Figure 12) clearly demonstrates the dominance of large submesoscale turbulent structures over smaller scale turbulence. This is further demonstrated by all turbulent spectra presented in this paper (
Figure 11,
Figure 13,
Figure 15 and
Figure 17), where the spectral energy sharply increases with length scale. Therefore, an estimate of the upper ocean turbulent kinetic energy is expected to be highly sensitive to the choice of the upper length scale limit. There does not appear to be a natural minimum indicating a separation between the small-scale turbulence presumably fed by surface forcing and larger submesoscale 2D turbulence, which is presumably fed by the energy cascading from even larger mesoscale oceanic currents, or other coastal mechanisms. Therefore, our choice of
λ = 500 m for the upper limit is only motivated by sensor resolutions and ensemble sizes.
Having computed the TKE contained within the 100–500 m range, the results between the ADCP time series and five individual realizations from dye plume velocimetry are first compared in
Figure 9. On all five occasions the airborne estimates are either nearly equal (once) or well below the ADCP estimate. An exact match between the two methods was not expected, as the ADCP might have been sampling a slightly different subsample of the flow from where the plume was located (typically within a several kilometer radius). However, the fact that none of the five aircraft realizations exceed ADCP values suggests a systematic bias. This could be in part due to measurement depth difference, where ADCP sampled at 10 m depth, whereas the dye plume velocity is sensitive to currents closer to the surface. However, that bias was mostly removed by filtering out small scales. If some bias remained, it would likely be larger, not smaller, favoring currents closer to surface, captured by the plume. More likely, the observed bias is due to the plume’s finite thickness and long time averages (discussed in more detail in
Section 2.3), which results in the plume’s inability to resolve small-scale turbulent features. It is likely that some of that bias still exists in the 100–500 m range and thus causes lower values seen in
Figure 9. This hypothesis is further supported by comparing velocity power spectra in
Figure 13. On small scales, all five realizations of the TKE power spectra obtained from dye plumes start well below the average ADCP spectrum over that time frame, and proceed approximately parallel to the expected slope
λ1, although high levels of noise in these spectra make exact estimation problematic. However, by
λ > 1000 m (or ×100 times the mixed layer depth), spectral levels catch up, indicating the gradual disappearance of the bias with length scale. Another interesting feature of these spectra at these larger scales (
λ > 1000 m) is the apparent change of slope to
λ3, perhaps indicating the start of the quasi-geostrophic turbulent cascade, known to follow that slope well into the mesoscales. For example, similar spectral slope and its flattening on smaller scales was suggested by [
43].
Our inability to convert infrared image pairs, such as
Figure 14, into velocity fields is, of course, disappointing. Notably, in a similar experiment over a river, sufficiently feature-rich flow was observed with an airborne infrared sensor, its velocities estimated, and favorably compared to boat-mounted ADCP by [
22]. The lesson learned here for future purposes is to take into consideration the expected availability of small-scale thermal contrast as a part of the experiment planning. The presence and the strength of small-scale thermal features needed for high fidelity Pattern Tracking Velocimetry, which in the open ocean primarily depends on the net air-sea heat flux, can and should be estimated and factored into go/no-go decision for an aircraft flight. Meanwhile, data contained in this study (e.g.,
Figure 14) can provide only qualitative information about the 2D spatial structure of the upper ocean turbulence. It reveals in detail the shapes, the typical length scales, the orientation, the anisotropy tendencies, and even widely disparate turbulent regimes (i.e., lower 4 km versus the rest of the swath) within the swaths. These images, unlike any other, demonstrate the immense complexity of the turbulent processes we are aiming to resolve and understand.
One useful quantity that can be obtained from these infrared swaths is the temperature power spectrum, shown in
Figure 15. Unlike other airborne methods, 1 m is the true resolution of this dataset, and hence the unique feature of the obtained spectrum is the seamless connection across four orders of spatial scales from 1 m to 10 km. The spectrum apparently starts by following
λ5/3 power law on the smallest scales up to
λ ≈ 10 m, then relaxes to ≈
λ1 for the rest of the resolved range. While it is tempting to suggest the correspondence to Kolmogorov’s 5/3 turbulent cascade on small scales and the correspondence to the
λ1 slope observed by the ADCP in
Figure 11, there are no physical grounds to assume so. This would mean not only suggesting a proportionality between the magnitude of temperature and velocity fluctuations, but also suggesting that this proportionality coefficient holds constant across this vast range of resolved scales, which we can neither confirm nor deny based on the results of this study.
One way in which we envision thermal imagery can be used quantitatively is by means of numerical flow simulations. For example, if a Large Eddy Simulation model attempts to resolve upper ocean currents on these scales, it can solve for temperature as one of the unknowns. Then the model output can be used to generate similar surface temperature imagery, to compute temperature power spectra, which can then be compared to observations. Although not direct, a positive match will serve as a strong indirect indication that the velocity fields produced by the model are accurate as well.
MSAR was able to obtain quantitative spatial maps of ocean surface velocities (cross-track component of the velocity vector) with approximately 10 m resolution and ≈5 cm/s velocity precision. Additionally, this paper represents a rare attempt to compare airborne interferometric SAR velocities to in situ data. The compared data sample is very limited, but valuable, as only few attempts of this kind were described in previous literature [
28], leaving much room for a more comprehensive validation study in the future. Other most closely related active microwave current retrieval and validation studies employed methodologies based on offshore platform or ship-based marine radars and reported successful comparisons to bottom-mounted ADCP and surface drifters in situ velocity measurements [
24,
44]. Unlike other velocity estimates shown in this paper, MSAR obtains an instantaneous snapshot of true surface velocities (i.e., the velocity with which the surface carries ≈3 cm long capillary waves). Kinetic energy fluctuations observed by MSAR are expected to be stronger, due to the presence of the dominant wave energy and due to the sampling of the very top of the mixed layer, where the turbulence is expected to be more energetic than the rest of the water column, especially on smaller scales. Indeed, MSAR’s velocity power spectrum, shown with the red curve in
Figure 17, places above the average ADCP spectrum. This contrasts with the dye plume velocimetry spectrum, which placed below the same ADCP spectrum on all but the largest spatial scales (recall
Figure 13). However, once the wave energy spectrum is considered (blue curve in
Figure 17), it appears that most of the small-scale energy in MSAR’s estimate comes from waves. The expected amount of wave energy is apparently underestimated, due to MSAR’s spatial resolution limitation of ≈10 m, causing it to miss some of the wave energy. Note, below 10 m a spatial filter was applied to MSAR’s interferogram to remove high wave number noise. A series of harmonics seen on the smallest scales of MSAR spectrum are primarily an artefact associated with that filtering. Both MSAR and wave buoy power spectra peak at a few tens of meters, after which they sharply diverge, indicating the rise of surface current contribution dominance. Therefore, it is the difference between MSAR and wave buoy spectra that is most indicative of the surface current spectra, and is indeed more in line with the
λ1 ADCP spectrum shown in the figure. Nonetheless, the absolute value of the MSAR spectrum appears to be noticeably larger than the ADCP, although that difference does appear to decline towards largest length scales. The swath width limitation does not allow resolving MSAR’s spectrum into larger scales, but if the observed trend persists, MSAR’s velocity spectrum is expected to intersect ADCP’s at
λ equal to few kilometers, which is similar to where the dye plume spectrum of that day crossed the same ADCP curve (red line in
Figure 13).
Large spatial filtering windows were applied to MSAR’s swath (
Figure 16) to eliminate wave signal. It was able to reveal underlying currents only after the window size was increased up to 200 × 200 m. This is in line with the expectation based on the spectra in
Figure 17, since the MSAR’s spectrum begins to predominantly consist of current energy only above
λ > 200 m. Apart from the thermal swaths, the resulting filtered spatial image of MSAR’s surface currents (bottom panel of
Figure 16) is the only other view into the 2D structure of submesoscale currents we were able to obtain. However, no detailed comparison between turbulent structures revealed by thermal and by MSAR swaths was undertaken here due to the fundamental differences in physical meanings behind these signals.
5. Conclusions
This paper presents an attempt at resolving upper ocean currents by means of various airborne remote sensing methods, including visible, infrared, and microwave bands of the EM spectrum. The airborne effort is accompanied by conventional underwater acoustic measurements of the vertical current profile, used to evaluate and validate the performance of airborne retrievals. The major conclusion is that airborne remote sensing methods can capture surface currents along the aircraft’s swath and thus provide a unique insight into the turbulent processes taking place on a wide and largely unresolved range of spatial scales between meters and tens of kilometers. However, these capabilities come with several important caveats and limitations, primarily related to turbulent length scale sensitivity and water depth sensitivity associated with specific airborne methods.
Visible band imagery of the upper ocean combined with a release of a long dye plume was found to be a powerful technique for resolving surface velocities and their power spectrum on the scales from ~100 to 10,000 m. However, the depth reference of retrieved velocities is uncertain, hence observed horizontal velocities are attributed to the overall horizontal motion of the mixed layer. Hence, this technique is limited to observations of 2D turbulence with length scales at least an order of magnitude greater than the depth of the mixed layer.
Infrared imagery was demonstrated to be a powerful tool for visualizing detailed 2D structure of the upper ocean turbulence. Additionally, it provided valuable surface temperature statistics in the form of a temperature spectrum on the scales from 1 to 14,000 m. However, its potential ability to produce surface velocity field was not realized due to insufficient signal to noise ratio in the small-scale thermal pattern.
The airborne MSAR combined with the new MCATI processing algorithm was able to resolve swaths of surface velocities (across-track component) with the unprecedented 10 m resolution and 5 cm/s accuracy. The resulting ≈1200 m wide interferogram swaths are instantaneous surface velocity snapshots, which contain turbulent current motions, but are also dominated by surface gravity wave orbital motions on small scales. A comparison to a co-located wave buoy spectrum, as well as spatial window filtering allows isolating submesoscale turbulence on the scales above the wave dominance, in this case λ > 200 m.