Optimizing the Remote Detection of Tropical Rainforest Structure with Airborne Lidar: Leaf Area Profile Sensitivity to Pulse Density and Spatial Sampling

Abstract

Airborne Laser Scanning (ALS) has been considered as a primary source to model the structure and function of a forest canopy through the indicators leaf area index (LAI) and vertical canopy profiles of leaf area density (LAD). However, little is known about the effects of the laser pulse density and the grain size (horizontal binning resolution) of the laser point cloud on the estimation of LAD profiles and their associated LAIs. Our objective was to determine the optimal values for reliable and stable estimates of LAD profiles from ALS data obtained over a dense tropical forest. Profiles were compared using three methods: Destructive field sampling, Portable Canopy profiling Lidar (PCL) and ALS. Stable LAD profiles from ALS, concordant with the other two analytical methods, were obtained when the grain size was less than 10 m and pulse density was high (>15 pulses m⁻²). Lower pulse densities also provided stable and reliable LAD profiles when using an appropriate adjustment (coefficient K). We also discuss how LAD profiles might be corrected throughout the landscape when using ALS surveys of lower density, by calibrating with LAI measurements in the field or from PCL. Appropriate choices of grain size, pulse density and K provide reliable estimates of LAD and associated tree plot demography and biomass in dense forest ecosystems.

1. Introduction

Measuring the density and distribution of leaves in forest canopies is key to understanding ecological and microclimate processes that drive forest functions [1,2,3,4,5,6]. The spatial structure of a leaf area influences or is influenced by light transmittance and absorbance, biodiversity conservation, carbon fluxes, ecophysiology, leaf phenology, disturbances, and water and climate interactions [2]. Advances in laser remote sensing have transformed the way forest canopies are measured, allowing a detailed inference about a canopy’s spatial structure with increasing application to leaf area estimation per se. Airborne Laser Scanning (ALS)—i.e., scanning lidar (Light Detection and Ranging)—has been used to model the leaf environment, obtaining attributes such as Leaf Area Index (LAI) and its decomposition into Leaf Area Density (LAD) distribution within the vertical canopy profile [4]. While lidar has proven its reliability and accuracy for canopy height and above-ground biomass estimation at different spatial scales [7,8], previous studies have also detected considerable sensitivity to laser acquisition parameters (e.g., pulse density) and processing methods (e.g., binning resolution) [9,10]. Yet, to date, little is known about how these factors alter the estimation of a leaf area and of LAD profiles specifically [11]. Thus, the stability and robustness of estimates of leaf area attributes from lidar require further investigation.

LAI represents the area of leaves per unit of ground area (m²·m⁻²). In the field, LAI can be estimated indirectly by raising a pole through the canopy and counting how many times the pole touches a leaf along the vertical profile [12]. The frequency of leaves in units along the vertical profile yields the LAD distribution, expressed as the leaf area at each height interval per volume of canopy (m²·m⁻³). LAD values are, thus, the partial volumetric components of LAI. Measuring LAD and LAI by destructively harvesting and scanning leaf area in a fixed footprint may be the most accurate approach for LAD profile quantification, but it is very difficult and laborious, especially in dense tropical forests [13,14]. Non-destructive, indirect techniques, such as vegetation indices from orbital sensors, the canopy gap area assessed through hemispherical photographs, and light intensity attenuation from paired above/below canopy light sensors, are commonly employed to estimate LAI. However, all three techniques have critical limitations. Vegetation indices are saturated in dense forests where LAI generally exceeds 4.0 [15,16]. The use of hemispherical photographs should be restricted to narrow time windows near dawn and dusk. Light sensors require a large open area or tower for an above-canopy measurement of light intensity close to each simultaneous understory measurement [17]. The signal of light sensors also becomes saturated in dense forests [18]. Alternatively, lidar systems are active sensors potentially free of these limitations—if they can effectively penetrate the full canopy depth. Indeed, lidar-derived estimates have revealed ecologically relevant differences in LAD profiles for different dense rainforest types, including those with LAI above 5.0 [4,5,19].

The MacArthur–Horn equation is commonly used for estimating LAI and LAD from discrete return lidar data [3,4,5,11,20,21,22]. This model follows the principle of the Beer–Lambert Law, which estimates the concentration of an absorbing compound mixed in a transparent liquid, according to the fraction of incident light that is transmitted [23]. In the MacArthur–Horn equation the concentration of the substance is replaced by the density of vegetation within a unit of the canopy volume (voxel). Here, the incident light intensity is the number of lidar pulses entering each voxel in a stack and the attenuation of transmittance is caused by the presence of leaves obstructing some of those pulses, which are then detected by the lidar sensor [21]. Key assumptions of the MacArthur–Horn equation as applied to LAD estimates are that leaves are distributed randomly inside voxels, that they do not transmit pulses, and that pulses are parallel and emitted vertically. For estimating a leaf area instead of a plant area (which includes non-leaf surface areas) with this method, an additional assumption is that a leaf area is a constant fraction of the plant surface area that determines the lidar pulse transmission so that a constant can scale profiles to LAD.

From a nadir view of airborne lidar, taller leafy crowns partially occlude lower ones, influencing the retrieval of information from underneath the topmost parts of the canopy. For this reason, the quality of the LAD profile estimation might be highly influenced by the lidar pulse density, with higher pulse numbers better sampling the lower portion of the canopy. The other factor that influences the apparent lidar pulse density when sampling LAD profiles is the horizontal binning resolution (grain size). There is an inherent relationship between lidar pulse returns per voxel and the horizontal grain size [24]; the larger the grain size, the more pulses within a voxel and in the profile sample generally. While higher sampling is desirable, increasing grain size may mask effects of low lidar pulse densities leading to poor sampling low in the canopy (e.g., in the understory). Furthermore, a leaf area is clumped at multiple spatial scales, and clumping influences the estimation of the leaf area by optical transmission methods, including the MacArthur–Horn method [25]. Thus, there is a clear need to assess the accuracy and the scale dependency of the LAD profile estimation as a function of the lidar pulse density and grain size. However, no previous studies have been devoted to evaluating how the lidar pulse density and the grain size employed affect estimates of LAD and LAI in tropical forests.

To address these dependencies in an ALS-based LAD profile estimation, a comparison approach is needed. Comparison possibilities include other very high-density lidar-based approaches, and destructive surveys. Recent studies have estimated the LAD profiles using a very high pulse density system, known as Portable Canopy profiling Lidar (PCL) which operates from the ground by emitting pulses skyward through the canopy [19,21,26,27]. The vegetation profiles obtained by PCL can be used to validate vegetation profiles derived from lower pulse density airborne systems [4]. Where PCL measurements overlap with independent measurements of LAI, the system can be calibrated to estimate a leaf area (not plant area), and where destructive sampling exists, a more complete validation is possible [4].

Our objective in this study was to determine the optimal parameters for reliably estimating LAD profiles from ALS data in dense tropical forests. We assessed LAD profile stability and accuracy associated with changes in (i) laser pulse density and (ii) grain size (voxel horizontal binning resolution). The ALS-derived LAD profiles were compared to those from destructive field sampling (from Reference [13]) and from the PCL.

2. Material and Methods

Lidar data were collected at the Ducke Forest Reserve (DFR; Figure 1). (02°55′S, 59°59′W). The DFR covers 10,000 ha of dense upland (terra firme) tropical forest. It has a mean LAI of 5.7, 790 trees ha⁻¹ (DBH > 10 cm), ~300 Mg ha⁻¹ of above-ground biomass [13,28] and ~1170 tree species [29]. The Köppen climate type is Af, mean annual temperature is 26 °C and the mean annual rainfall ranges between 2400 and 2700 mm. The drier months are typically August and September, with less than 100 mm of rainfall per month. The ALS data covered 12.5% of the total area of the Reserve, in three strips (Figure 1). Elevation above sea level of the area covered by ALS scanning varies from 30 to 90 m. Mean canopy height is 27 m, with the tallest trees reaching up to 55 m (as measured in the canopy height model derived from ALS).

ALS data were collected in June 2008 using a Leica ALS50 system (Heerbrugg, Switzerland) on board a Navajo EMB 820C (Embraer Ltd., São José dos Campos, Brazil), operating at a pulse rate of 100 KHz, maximum 5° off-nadir view angle, ground beam diameter of 12 cm (a.k.a. lidar footprint), mean flight altitude of 816 m above ground level (providing overlap of 27%), and a Novatel OEMv4 GNSS receiver. Lidar data were georeferenced in the Universal Transverse Mercator (UTM) 20S coordinate system using the WGS84 datum. The acquired ALS point cloud has a mean density of 42 pulses m⁻² (considering only the first returns). This high density was crucial for the data thinning objectives of this paper.

Ground returns were identified using all returns (of which 77% were first returns), using the Kraus and Pfeifer algorithm [30] implemented in FUSION/LDV [31], using the command “GroundFilter” with a window size of 8 × 8 m and the default values for all other parameters. This produced a cloud of ground-returns with a mean density of 0.9 returns m⁻². The bare ground elevation was then interpolated to a 2 m horizontal resolution by simple kriging implemented in the R environment [32] with the lidR package [33]. This ground elevation was subtracted from the elevation of each ALS return to obtain its above-ground height, and all analyses were conducted on these ground elevation-corrected data (a.k.a. normalized cloud).

The next step was to subsample pulse returns to create lidar samples with different rarified pulse return densities. Considering just first return pulses at a 1 m horizontal resolution (finest grain size considered), we randomly thinned pulse densities to 30, 25, 20, 15, 10, 5, and 2 pulse returns m⁻² (Figure 2). While some thinning algorithms are devoted to reproduce the spatial variation of scanning patterns, several authors [10,24,34,35] employ thinning methods like ours, which best control the final density of each simulation. Whenever a cell’s true pulse density was lower than the target rarified density, all the available pulses were used. The first-return point cloud was then binned into voxels (canopy volume units) and the number of first returns within each voxel was calculated for LAD estimation (next paragraph). We analyzed voxels at seven horizontal grain sizes: 1, 2, 5, 10, 25, 50 and 100 m. The vertical resolution (Delta Z or Dz) was fixed at 1 m (Figure 3) to maximize the potential to recover vertical forest structural information [5]. ALS data were analyzed for 24 one-hectare field plots of 100 m × 100 m. Each plot was traversed by an associated 250 m long upward-looking ground PCL transect (See [4] for additional description).

For each combination of voxel size and pulse return density, we calculated the number of pulses that entered each voxel i (pulses.in_i) and the number of pulses that passed through that voxel (pulses.out_i). Since we used a maximum of 5° off-nadir view in the ALS survey, we could work under the assumption that each lidar pulse is vertically incident. This means that we could track the passage and reflection of pulses within voxel columns to calculate the estimated pulses entering the tops of voxels and the pulses leaving the bottoms of voxels. All entering pulses that were not detected as returns from a voxel were assumed to pass through and enter the next voxel in a column. The MacArthur–Horn equation (Equation (1)) was applied for each voxel to compute its Leaf Area Density (LAD_i) (Figure 4)

$$LA{D}_i=\ln \left(pulses.i{n}_i/pulses.ou{t}_i\right)\times \frac{1}{Dz}\times \frac{1}{K}$$

(1)

Dz is the vertical resolution, fixed at 1 m. The K coefficient performs an inverse linear calibration of LAD to a known LAI. It can be assumed to be constant if certain factors remain fixed (e.g., lidar beam width, pulse intensity, pulse wavelength, distribution of leaf blade angles, degree of clustering of leaves, contribution of non-leaf area to returns). While the choice of the K coefficient changes the LAD values, and consequently the derived LAI estimate, the relative LAD proportions found along the vertical strata are unaffected by K. We fixed K = 1, so we calculated an “effective LAD” and “effective LAI”. For convenience, these are hereafter referred to as simply LAD and LAI. The K coefficient effect is addressed in detail in the discussion section. Suffice it to say here that K = 1 does produce an LAI close to the field measured LAI [13], when the grain size is large.

Occluded voxels—those where pulses.out = 0, or pulses.in = 0—were assigned as no-data (NA). After applying the MacArthur–Horn equation to all voxels, the mean LAD for each one-meter vertical stratum across a one-hectare field plot was obtained. Note that NA voxels are not considered when calculating the mean LAD of a stratum; in effect, the horizontal area is renormalized to discount these areas with NA-values, which have not been sampled by lidar pulses. The mean LAI for the entire plot was simply the sum of the mean LADs from each stratum (Figure 4).

The PCL data were collected in April 2009 using last returns from an upward-looking Riegl model LD90-3100VHS-FLP (Horn, Austria), along the 24 transects of 250 m in length. These transects overlap the 1-ha ALS plots (Figure 1). The locations of the ALS plots were limited to areas with high and homogeneously distributed return density so that the point clouds could be thinned to target densities. As a result, ALS plots do not always coincide with the ground lidar transects. Although some of the 1-ha ALS plots and PCL transects are not spatially paired, care was taken to ensure similar conditions, particularly the hillslope position (elevation). The PCL instrument operates at a pulse rate of 1 KHz. Since the lidar survey is a vertical profile of the canopy and the data is acquired along a transect, the PCL produces a 2-D point cloud (height above ground × along-track distance). The instrument is attached to a gimbal to maintain a vertical upward aim. A small 12 V battery and a water-resistant computer complete the system [19]. The operator walks at a constant pace, using an electronic metronome and field markers spaced every two meters. Walking at a speed of half a meter per second, the PCL emits a total of 2000 pulses per meter along the transect. For vertical and horizontal resolutions, the PCL-based LAD profiles used Dz = 1 m and Dx = 2 m, respectively [4,19]. The LAD strata estimated from both ALS and ground lidar were limited to pulse returns above one meter from the ground. This avoids ground-return interference in the ALS data and is also imposed by the ground lidar sensor height.

To investigate the effects of pulse density and grain size on the Airborne Laser Scanner LAD profile estimation, we obtained LAD at each 1 m height interval averaged over the 24 plots. We first examined the change of the mean LAD profile (average of 24 plots) in absolute values (m² ·m⁻³; K = 1) with varied grain size and pulse density. We then compared, also as a function of grain size and pulse density, the behaviors of (i) the 24-plot mean ALS profile of relative LAD (LAD as % of LAI, which cancels K); (ii) the 24-transect mean profile of ground lidar-derived relative LAD; and (iii) a mean profile of directly measured relative LAD, collected from four mature old growth forest plots of 100-m² close to the Ducke Forest Reserve [13]. Utilizing Reference [13] for comparison, we assume that the average forest structure is stable through time (see also Reference [4]), and indeed this forest with low turnover has not been implicated in any major disturbance processes [29]. Finally, we investigated the stability of the ranking (by Spearman rank correlations) of the 24 plots by their LAI value (using K = 1), as a function of different grain sizes and pulse densities.

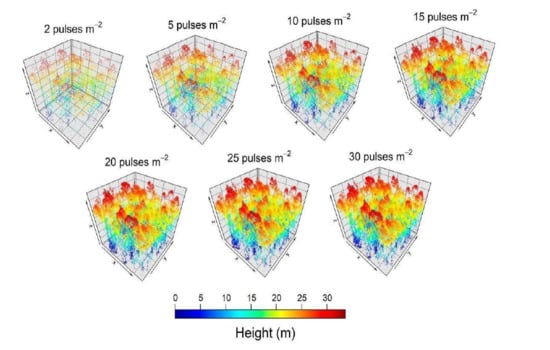
3. Results

Vegetation profiles expressed as absolute LAD (m²·m⁻³), using fixed K, tended to stabilize when the grain size reached 10 m, independent of pulse density or when the pulse density reached 15 pulses m⁻², regardless of grain size (Figure 5). Within each of the smaller grain sizes (1, 2, and 5 m), LAD estimations increased logarithmically with pulse density, until saturating at 15 pulses m⁻². As the grain size increased from 1 m to 10 m, understory LAD increased greatly and LAD in the upper canopy decreased slightly, shifting the overall shape of the profile.

The 24-hectare mean profile of relative LAD, expressed as a percentage of LAI, was unaffected by pulse density (Figure 6). Increasing the grain size had the same effect of shifting the profile observed in the profiles with absolute LAD values; the upper canopy decreased and the lower canopy increased its leaf density. A stability at large grain size did not lead to improved accuracy—increasing the grain size also increased the difference between the ALS profile and the profiles derived from field measurements and ground lidar.

The ranking of the 24 plots by their LAI values was completely stable with respect to pulse density. Spearman Rank Correlation was 1.0 across all seven classes of pulse density. This was true at all seven grain sizes (Figure 7). Ranking of plots by their LAI was affected somewhat by different grain sizes: Rank Correlation was 0.83 across all seven classes of grain size, when evaluated separately for each pulse density class and then averaged (Figure 8). However, if considering only the four smaller grain sizes in Figure 8 (1 m, 2 m, 5 m, and 10 m), the ranking of plots by their LAI was very stable as a function of grain size, with Rank Correlation = 0.95.

4. Discussion

4.1. Grain Size and Pulse Density Effects on LAD and LAI

To the best of our knowledge, this is the first study to assess the impacts of ALS pulse density and voxel resolution on the estimation of LAD profiles and LAI, using the MacArthur–Horn equation (Beer–Lambert Law) applied to small-footprint ALS lidar in a tropical forest. In general, the LAD and LAI estimates tended to stabilize with an increasing grain size and increasing ALS pulse density. At small grain sizes of 1 m, 2 m, and 5 m, absolute LAD profiles became stable at respective pulse densities of 15, 15, and 10 pulses m⁻². At grain sizes of 10 m or larger, pulse density can be as low as 2 pulses m⁻² and still provide a LAD profile very similar to those obtained at higher pulse density (Figure 5).

The ideal combination in the trade-off between pulse density and grain size hinges on accuracy. Smaller ALS grain sizes (≤5 m) showed better agreement with the vegetation profiles from destructive field measurements and from PCL ground lidar (Figure 6). This is particularly evident when comparing ALS results to those obtained by field measurements in the portion of the vegetation profile below ~4 m height. Grain sizes ≥ 10 m will overestimate vegetation in this portion of the profile, particularly when pulse density is high. For lidar surveys with lower pulse density, a grain size of 10 m may be effective, and may mitigate some of the unwanted artificial shift in vertical LAD distributions observed at larger spatial scales. Increasing the grain size to the point that it approximates the length scales of branches or whole trees—primary elements of leaf architectural support—might create strong leaf clumping and thus violate the MacArthur–Horn assumption of random leaf distribution. This could may explain the increasing LAD profile errors that we observed with the increasing grain size.

An LAD estimation based on multitemporal ALS data [11] included a correction to enhance inter-comparability across multiple laser sensors. The pulse return density had little appreciable bias impact above 20 returns m⁻² using a grain size of 2 m for plots with 0.25 ha.

Our results show that a very consistent LAI ranking of different sites can be obtained independent of pulse density. Relative LAD values were useful for assessing potential scale dependencies in the shape of LAD profiles and have the advantage of cancelling the effects of the K coefficient. But this comes at the cost of removing LAI as an attribute. LAI is a critical site descriptor for the study of canopy structure and function.

Less expensive, low pulse density ALS contracts may be able to provide consistent discrimination of sites based on density and distribution of leaves. We caution, however, that the lower accuracy particularly of the LAD profile estimation at a coarse grain size or at low pulse densities may be unacceptable for some applications, particularly in models and methods that rely on the fine scale vertical and horizontal heterogeneity of the canopy structure to make ecological inferences. Examples include the estimation of timber stock or demographic structure [5] or light interception and absorption (if the methods of Reference [6] were applied to ALS data). For these applications our results suggest that pulse densities of 20 pulses m⁻² or greater and grain sizes between 2 and 5 m, which maximize accuracy and stability, should be utilized.

Our results agree with classic ‘optical probe’ based investigations of leaf area estimation. One study [36], using the MacArthur–Horn equation and point-quadrat sampling [12,37], also found a positive relation between LAI estimates and sample size, analogous to our Figure 7. They showed that, despite a sample size effect impacting absolute LAD values and LAI, the fraction of LAI in each vertical stratum was nearly constant over different sample sizes. In apparent agreement, we found that for small grain sizes, the vegetation profile shapes are stable with respect to pulse density if LAD is expressed in relative units (% of LAI), while absolute LAD profiles converged to a stable shape (and LAI) only with high pulse density (≥15 pulses m⁻²) (Figure 5 and Figure 6).

4.2. Tackling Occluded Voxels

At small grain sizes, the number of occluded voxels (no-data voxels) increases and one must take care to avoid their influence on the mean plot-wide LAD profile shape and mean plot-wide LAI (or transect mean LAI, in the case of ground lidar). No-data voxels do not affect the mean LAD obtained across all voxels at the same above-ground height across a plot. Plot-scale mean LAI obtained from the sum of these stratum means will be a proper estimate [4,5,19]. However, if one sums the LAD values in each voxel column to obtain the LAI at each horizontal grid footprint in the forest, each of these sums will be affected by the number of no-data voxels in their respective columns. A mean plot-wide LAI from these column LAIs will be incorrect. Such a column-level LAI mapping must consider columns with any no-data voxels to have no LAI data as well. In a Swiss deciduous forest, with a pulse density of 11 pulses m⁻² and grain size of 1 m, it was found that at least 25% of the forest canopy volume remains occluded in the ALS data [38]. Here we found a similar result, with 29, 23, 10 and 3% occluded when grain size is, respectively, 1-, 2-, 5- and 10-m and pulse density is fixed at 10 pulses m⁻². In this sense, larger grain sizes effectively mask areas that are occluded in the canopy that fall within voxels with varied pulse sampling. Furthermore, the spatial structure of occluded areas may create apparent leaf area clumping that influences leaf area estimation. Our expectation is that the same grain sizes that produce maximal correspondence with PCL and destructive LAD profile data (i.e., ≤5 m) also optimize LAI estimation accuracy for comparisons.

We here assume that the LAD of a visible voxel at any given height provides an unbiased estimate of the LAD of occluded voxels at that height. In forests with many gaps, the upper canopy surface, which is never occluded to the ALS, frequently dips to lower heights. The canopy surface generally has high LAD as it is well illuminated by the sun, so these always visible voxels of low height in gaps could have higher LAD than occluded voxels in the dark understory at the same height. Therefore, though forests with a lot of gaps should have a high mode of LAD in the lower mid-canopy, this mode may be exaggerated. The PCL provides a test of this bias because the LAD in shaded understory is not occluded from the perspective of the PCL. Whether using upward looking PCL or downward looking ALS, in gap-rich forest one observes an LAD profile of the same shape with mode in the same position [4]. This suggests that no significant bias is present.

4.3. Calibrating the K Coefficient

In the absence of a known calibration LAI from a reference site, some authors have used K = 1 [19,22]. However, for accurate values of absolute LAI, particularly at low pulse densities for which lower portions of the canopy will have many no-data voxels, the coefficient K should be adjusted to calibrate estimated LAI to a correct, independently measured LAI (Equation (2)). An alternative is to calibrate K with a given lidar system at a reference LAI site and then estimate LAI with that same system for another site with unknown LAI, under the assumption that leaf properties such as clumping and leaf angles that could affect K-calibration are constant (see Reference [25]). Calibrated K is obtained as the ratio between the mean LAI derived from lidar (LAI_K=1) and the correct mean LAI of the reference site (LAI_Site):

$$K=\frac{LA{I}_{K=1}}{LA{I}_{Site}}$$

(2)

Figure 9 shows the appropriate K values for maintaining agreement between ALS-derived LAI and a field-measured mean LAI of 5.7 (field measurements from Reference [13]). For large grain sizes, a K value close to 1.0 gives the expected field-derived LAI value, independent of pulse density. Calibrated K is clearly sensitive to both grain size and pulse density and much more so at lower grain sizes and lower pulse densities. It tends to stabilize as pulse density increases but remains sensitive to grain size even at high pulse densities. The robustness of the K-curves in Figure 9 is still unknown. Different forest types with different species composition, leaf orientation and leaf clumping may produce varied relations between grain size, pulse density and the K coefficient. Probably forest types with lower LAI present better results with lower pulse densities, since obstruction is also reduced.

4.4. Limitations of This Study

We found a discrepancy between PCL and ALS profiles at 1–4 m (low-canopy) height, which should not be considered when evaluating ALS accuracy in tropical forests with dense understory vegetation (Figure 6). This is attributable to removing some of the understory, mainly palm fronds, to allow passage of the ground lidar operator at a constant walking speed. Although the ALS LAD profiles (using grain size of 1 and 2 m) at the lowest portion of the canopy are very similar to those from field destructive samples, and the Ducke site is characterized by dense understory vegetation (particularly palms; [29]), it is possible that this increase of LAD at low-canopy height is an effect of ground estimation errors (ground returns not classified as ground points). The lowest pulse penetration and highest error is expected in the understory with ALS data. Future work should take care to exclude low positions from analysis (or explore corrections) when appropriate. We also note that ground estimation errors will increase as sampling density decreases over ALS collections, particularly in heterogeneous terrain [39], a factor that was not considered in our analysis since ground surfaces were estimated prior to pulse rarefactions.

We used four profiles of field collected LAD from small patches of dense forest as our “gold standard”. However, the true mean profile of LAD across a larger landscape will include forest gaps. These should affect the shape of the mean profile of LAD, increasing LAD in the lower half of the profile.

Many other factors (e.g., instrument type, beam divergence, scan angle, flight altitude, along-track and cross-track footprint spacing) could influence relationships between grain size, pulses density and the estimation of LAD profiles. For example, our study used a maximum of 5° off-nadir scan angle; higher scan angles may introduce biases in LAD profiles since one of the key assumptions of the MacArthur–Horn equation is that pulses are parallel and emitted vertically. Higher flight altitude would increase ground footprint size, which could decrease penetration rates and increase occlusion problems, all else being fixed [40].

In practice, low pulse densities, shown in our study to be sufficient for obtaining LAD profiles, may be associated with high altitude flights and wide scan angle collections, to maximize coverage at low cost. The effects of wide angles (e.g., +/− 30 degrees), and the larger pulse footprints expected from greater beam divergences, on estimates of LAD profiles still require study. To improve comparability with our study, LAD profiles could be extracted from only near vertical angles found closer to the flight track, where the MacArthur–Horn equation assumption of vertical pulse transmission is better satisfied.

5. Conclusions and Implications for Future Research

For an accurate and stable estimation of LAD profiles and of LAI from ALS data in tropical rainforests, we recommend voxels with a small grain size (<10 m) only when pulse density is greater than 15 pulses m⁻². For pulse densities less than 15 pulses m⁻² we recommend a 10 m grain size. We also highlight the importance of using a calibrated K coefficient in the MacArthur–Horn equation, particularly so when using small grain size (1–5 m) with low pulse densities. For stable ranking/discrimination of sites by their LAI values using fixed K, pulse density had no effect, and grain size had almost no effect for dimensions ≤10 m.

However, it is important to highlight that our results were obtained with a specific ALS instrument, forest type, and survey configuration. Thus, we have isolated pulse density effects per se. More field collected reference plots in different forest types (with different LAI values), and lidar data sets that include repeated collections with survey parameters systematically varied to explore not just pulse density but also scan angle, pulse footprint, and other factors’ effects, are recommended to improve understanding of LAD and LAI estimation from lidar. A recent study [11] found that flight parameters with different lidar sensors can affect LAD estimates differently. They developed a correction method to enhance inter comparability over multiple sensors. However, the individual effects of each parameter, such as the scan angle, still need to be better understood.

New lidar technologies, such as Geiger mode lidar (GML) and single photon lidar (SPL) [41], have the potential to generate a denser point cloud from a less powerful laser source obtained at an increased altitude, compared to the traditional “linear-mode lidar” (LML). Thus, it may be possible to estimate LAD at high horizontal resolution (~1 m) and lower costs. However, critics have found some cons about the new lidar technologies, such as the absence of the intensity image and a greater susceptibility to solar noise [41,42]. GML has the drawback of an inferior penetration in forested areas, while SPL is slightly better (similar to LML) [42].

Some studies have efficiently used full waveform lidar for LAI estimation from orbital platforms [43,44]. This technology will soon cover large areas of the Amazon and other tropical forests with resolution of approximately 25 m [45].

We also examined how analysis grain (as in Figure 5) impacts the vegetation profile estimation when we included all returns, not just the 77% which are first returns (Supplementary Materials Figures S1 and S2). The effect is to decrease the estimated upper canopy LAD values. This may be an artifact, however, since the MacArthur–Horn approach assumes that each pulse represents an independent canopy probe, while in fact second returns are effectively only possible after first returns (below first returns for airborne lidar) and so forth, for third and fourth returns. Thus, additional algorithm development and validation could lead to more accurate MacArthur–Horn LAD estimation from multiple return lidar data.

LAD profiles have seen a gamut of applications in recent tropical forest studies: Impact of fire and sensitivity to fire [19]; estimating tree diameter-class frequencies [5]; forest type discrimination; and radiative transfer and absorption modeling [3,4,6,46]. ALS-derived estimations of LAD profiles and of LAI provide unprecedented opportunities for estimating canopy structure and function, including modeling the leaf environments and forest demographic structure, on a broad spatial scale to address problems in forest conservation and management.