Studies of Internal Waves in the Strait of Georgia Based on Remote Sensing Images
Abstract
:1. Introduction
2. Materials and Methods
2.1. Data Introduction
2.1.1. Remote Sensing Data
2.1.2. Field Observation Data
2.2. Research Methods
2.2.1. Remote Sensing Derivation of Internal Wave Parameters
2.2.2. Extract Characteristics of Internal Waves from ADCP Data
2.2.3. Ray Propagation of Internal Waves
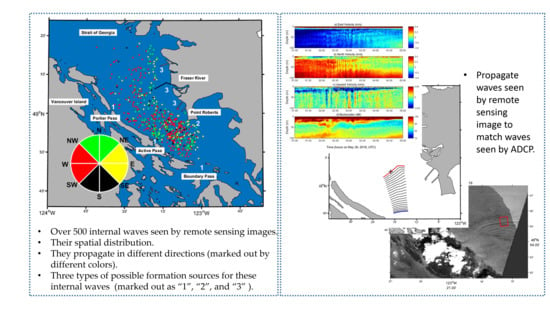
3. Results
3.1. The Distribution of Internal Waves in Space and Time
3.2. A Case Study
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Alpers, W. Theory of radar imaging of internal waves. Nature 1985, 314, 245–247. [Google Scholar] [CrossRef]
- Thompson, D.R.; Gasparovic, R.F. Intensity modulation in SAR images of internal waves. Nature 1981, 320, 345–348. [Google Scholar] [CrossRef]
- Shand, J.A. Internal waves in Georgia Strait. Trans. AGU 1953, 34. [Google Scholar] [CrossRef]
- Wang, C.; Pawlowicz, R. Propagation speeds of strongly nonlinear near-surface internal waves in the Strait of Georgia. J. Geophys. Res. Oceans 2011, 116. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Pawlowicz, R. Oblique wave-wave interactions of nonlinear near-surface internal waves in the Strait of Georgia. J. Geophys. Res. Oceans 2012, 117. [Google Scholar] [CrossRef] [Green Version]
- Wang, C.; Pawlowicz, R. Internal wave generation from tidal flow exiting a constricted opening. J. Geophys. Res. Oceans 2017, 122, 110–125. [Google Scholar] [CrossRef]
- Li, L.; Pawlowicz, R.; Wang, C. Seasonal Variability and Generation Mechanisms of Nonlinear Internal Waves in the Strait of Georgia. J. Geophys. Res. Oceans 2018, 123, 5706–5726. [Google Scholar] [CrossRef]
- Pawlowicz, R.R.O.; Halverson, M. The circulation and residence time of the strait of Georgia using a simple mixing-box approach. Atmos.-Ocean 2007, 45, 173–193. [Google Scholar] [CrossRef]
- Halverson, M.; Pawlowicz, R. Tide, Wind, and River Forcing of the Surface Currents in the Fraser River Plume. Atmos.-Ocean 2016, 54, 131–152. [Google Scholar] [CrossRef]
- Turner, J.S.; Benton, E.R. Buoyancy Effects in Fluids. Phys. Today 1974, 27, 52–53. [Google Scholar] [CrossRef]
- Hughes, B. The effect of internal waves on surface wind waves 2. Theoretical analysis. J. Geophys. Res. 1978, 83, 455–465. [Google Scholar] [CrossRef]
- Soontiens, N.; Allen, S.; Latornell, D.; Le Souef, K.; Machuca, I.; Paquin, J.P.; Lu, Y.; Thompson, K.; Korabel, V. Storm surges in the Strait of Georgia simulated with a regional model. Atmos.-Ocean 2016, 54. [Google Scholar] [CrossRef]
- Soontiens, N.; Allen, S. Modelling sensitivities to mixing and advection in a sill-basin estuarine system. Ocean Model. 2017, 112, 17–32. [Google Scholar] [CrossRef]
- Pawlowicz, R.; Di Costanzo, R.; Halverson, M.; Devred, E.; Johannessen, S. Advection, Surface Area, and Sediment Load of the Fraser River Plume Under Variable Wind and River Forcing. Atmos.-Ocean 2017, 55, 293–313. [Google Scholar] [CrossRef]
- Benjamin, T.B. Internal waves of permanent form in fluids of great depth. J. Fluid Mech. 1967, 29, 559–592. [Google Scholar] [CrossRef]
- Benney, D.J. Long Non-Linear Waves in Fluid Flows. Stud. Appl. Math. 1966, 45, 52–63. [Google Scholar] [CrossRef]
- Joseph, R.I. Solitary waves in a finite depth fluid. J. Phys. A Math. Gen. 1977, 10, L225–L227. [Google Scholar] [CrossRef]
- Kubota, T.; Ko, D.R.S.; Dobbs, L.S. Weakly-Nonlinear, Long Internal Gravity Waves in Stratified Fluids of Finite Depth. J. Hydronaut. 1978, 12, 157–165. [Google Scholar] [CrossRef]
- Ono, H. Algebraic Solitary Waves in Stratified Fluids. J. Phys. Soc. Jpn. 1975, 39, 1082–1091. [Google Scholar] [CrossRef]
- Baines, P.G. Topographic Effects in Stratified Flows. Eos Trans. Am. Geophys. Union 1995, 77, 151. [Google Scholar] [CrossRef]
- Chen, G.Y.; Su, F.C.; Wang, C.M.; Liu, C.T.; Tseng, R.S. Derivation of internal solitary wave amplitude in the South China Sea deep basin from satellite images. J. Oceanogr. 2011, 67, 689–697. [Google Scholar] [CrossRef]
- Rascle, N.; Nouguier, F.; Chapron, B.; Mouche, A.; Ponte, A. Surface Roughness Changes by Finescale Current Gradients: Properties at Multiple Azimuth View Angles. J. Phys. Oceanogr. 2016, 46. [Google Scholar] [CrossRef]
- Keller, W.C.; Wright, J.W. Microwave scattering and the straining of wind-generated waves. Radio Sci. 1975, 10, 139–147. [Google Scholar] [CrossRef]
- Alpers, W.; Hennings, I. A theory of the imaging mechanism of underwater bottom topography by real and synthetic aperture radar. J. Geophys. Res. Oceans 1984, 89, 10529–10546. [Google Scholar] [CrossRef]
- Kudryavtsev, V.N.; Akimov, D.; Johannessen, J.A.; Chapron, B. On radar imaging of current features. Part 1: Model and comparison with observations. J. Geophys. Res. Oceans 2005, 110. [Google Scholar] [CrossRef]
- Plant, W.J.; Keller, W.C.; Hayes, K.; Chatham, G.; Lederer, N. Normalized radar cross section of the sea for backscatter: 2. Modulation by internal waves. J. Geophys. Res. Oceans 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Scotti, A.; Butman, B.; Beardsley, R.C.; Alexander, P.S.; Anderson, S. A Modified Beam-to-Earth Transformation to Measure Short-Wavelength Internal Waves with an Acoustic Doppler Current Profiler. J. Atmos. Ocean. Technol. 2005, 22, 583–591. [Google Scholar] [CrossRef] [Green Version]
- Wang, C. Geophysical Observations of Nonlinear Internal Solitary-like Waves in the Strait of Georgia. Ph.D. Thesis, University of British Columbia, Vancouver, BC, Canada, 2009; p. 171. [Google Scholar]
- Watson, G.; Robinson, S. A study of internal wave propagation in the Strait of Gibraltar using shore-based marine radar images. J. Phys. Oceanogr. 1990, 20, 22. [Google Scholar] [CrossRef]
- Watson, G.; Robinson, S. A numerical model of internal wave refraction in the Strait of Gibraltar. J. Phys. Oceanogr. 1991, 21, 20. [Google Scholar] [CrossRef]
- Nash, J.D.; Moum, J.N. River plumes as a source of large-amplitude internal waves in the coastal ocean. Nature 2005, 437, 400–403. [Google Scholar] [CrossRef]
- Brandt, P.; Romeiser, R.; Rubino, A. On the determination of characteristics of the interior ocean dynamics from radar signatures of internal solitary waves. J. Geophys. Res. Oceans 1999, 104, 30039–30045. [Google Scholar] [CrossRef] [Green Version]
- da Silva, J.C.B.; Ermakov, S.A.; Robinson, I.S.; Jeans, D.R.G.; Kijashko, S.V. Role of surface films in ERS SAR signatures of internal waves on the shelf: 1. Short-period internal waves. J. Geophys. Res. Oceans 1998, 103, 8009–8031. [Google Scholar] [CrossRef] [Green Version]











| Satellite | ERS-1/2 (SAR) | ENVISAT-1 (SAR) | SENTINEl-1A/B (SAR) | Sentinel-2 (Optical) |
|---|---|---|---|---|
| Service time | 17 July 1991–29 January 2011 | 1 March 2002–21 April 2011 | 1A: 3 April 2014–now 1B: 26 April 2016–now | 2A: 23 June 2015–now 2B: 17 March 2017–now |
| Revisit period (day) | 35 | 35 | 12 | 5 |
| Resolution (meter) | 30 | 30 | 5×5 | 10 |
| Number of images | 189 | 156 | 164 | 46 |
| Number of internal waves | 218 | 168 | 74 | 74 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Wang, C.; Wang, X.; Da Silva, J.C.B. Studies of Internal Waves in the Strait of Georgia Based on Remote Sensing Images. Remote Sens. 2019, 11, 96. https://doi.org/10.3390/rs11010096
Wang C, Wang X, Da Silva JCB. Studies of Internal Waves in the Strait of Georgia Based on Remote Sensing Images. Remote Sensing. 2019; 11(1):96. https://doi.org/10.3390/rs11010096
Chicago/Turabian StyleWang, Caixia, Xin Wang, and Jose C. B. Da Silva. 2019. "Studies of Internal Waves in the Strait of Georgia Based on Remote Sensing Images" Remote Sensing 11, no. 1: 96. https://doi.org/10.3390/rs11010096
APA StyleWang, C., Wang, X., & Da Silva, J. C. B. (2019). Studies of Internal Waves in the Strait of Georgia Based on Remote Sensing Images. Remote Sensing, 11(1), 96. https://doi.org/10.3390/rs11010096