Fitted PROSAIL Parameterization of Leaf Inclinations, Water Content and Brown Pigment Content for Winter Wheat and Maize Canopies
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Site
2.2. In Situ Measurements
2.3. PROSAIL Environment
2.4. Variable Fitting
2.5. RGB Image Segmentation
3. Results
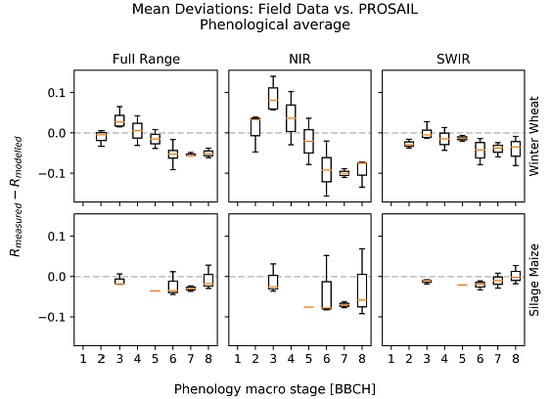
3.1. Deviations between Model and Measurement
3.2. Optimized Parameter Sets
3.2.1. The Fitting Process
3.2.2. Analysis of the Optimized Variables for Winter Wheat
3.2.3. Analysis of the Optimized Variables for Silage Maize
3.3. Seasonal Development of Winter Wheat Canopy Fractions in Sensor View
4. Discussion
5. Conclusions
Supplementary Materials
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Hanes, J. Biophysical Applications of Satellite Remote Sensing; Springer-Verlag: Berlin/Heidelberg, Germany, 2013; p. XIV, 230. [Google Scholar]
- Webber, H.; Ewert, F.; Kimball, B.; Siebert, S.; White, J.; Wall, G.; Ottman, M.; Trawally, D.; Gaiser, T. Simulating canopy temperature for modelling heat stress in cereals. Environ. Model. Softw. 2016, 77, 143–155. [Google Scholar] [CrossRef] [Green Version]
- Chalker-Scott, L. Environmental Significance of Anthocyanins in Plant Stress Responses. Photochem. Photobiol. 1999, 70, 1–9. [Google Scholar] [CrossRef] [Green Version]
- Daughtry, C. Estimating Corn Leaf Chlorophyll Concentration from Leaf and Canopy Reflectance. Remote Sens. Environ. 2000, 74, 229–239. [Google Scholar] [CrossRef]
- Gitelson, A.A.; Gamon, J.A.; Solovchenko, A. Multiple drivers of seasonal change in PRI: Implications for photosynthesis 1. Leaf level. Remote Sens. Environ. 2017, 191, 110–116. [Google Scholar] [CrossRef] [Green Version]
- Schweiger, A.K.; Schütz, M.; Risch, A.C.; Kneubühler, M.; Haller, R.; Schaepman, M.E. How to predict plant functional types using imaging spectroscopy: Linking vegetation community traits, plant functional types and spectral response. Methods Ecol. Evolut. 2017, 8, 86–95. [Google Scholar] [CrossRef]
- Van Der Tol, C.; Verhoef, W.; Timmermans, J.; Verhoef, A.; Su, Z. An integrated model of soil-canopy spectral radiances, photosynthesis, fluorescence, temperature and energy balance. Biogeosciences 2009, 6, 3109–3129. [Google Scholar] [CrossRef] [Green Version]
- Shangguan, Z.; Shao, M.; Dyckmans, J. Effects of Nitrogen Nutrition and Water Deficit on Net Photosynthetic Rate and Chlorophyll Fluorescence in Winter Wheat. J. Plant Physiol. 2000, 156, 46–51. [Google Scholar] [CrossRef]
- Zhang, Y.; Guanter, L.; Berry, J.A.; Joiner, J.; Van Der Tol, C.; Huete, A.; Gitelson, A.; Voigt, M.; Kohler, P. Estimation of vegetation photosynthetic capacity from space-based measurements of chlorophyll fluorescence for terrestrial biosphere models. Chang. Boil. 2014, 20, 3727–3742. [Google Scholar] [CrossRef] [Green Version]
- Pearce, R.B.; Brown, R.H.; Blaser, R.E. Relationships between Leaf Area Index, Light Interception and Net Photosynthesis in Orchardgrass1. Crop. Sci. 1965, 5, 553. [Google Scholar] [CrossRef]
- Richards, R. Selectable traits to increase crop photosynthesis and yield of grain crops. J. Exp. Bot. 2000, 51, 447–458. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Hank, T.B.; Bach, H.; Mauser, W. Using a Remote Sensing-Supported Hydro-Agroecological Model for Field-Scale Simulation of Heterogeneous Crop Growth and Yield: Application for Wheat in Central Europe. Remote Sens. 2015, 7, 3934–3965. [Google Scholar] [CrossRef] [Green Version]
- Sid’Ko, A.; Botvich, I.; Pisman, T.; Shevyrnogov, A. Estimation of chlorophyll content and yield of wheat crops from reflectance spectra obtained by ground-based remote measurements. Field Crops Res. 2017, 207, 24–29. [Google Scholar] [CrossRef]
- Thorp, K.; Wang, G.; Bronson, K.; Badaruddin, M.; Mon, J.; Thorp, K. Hyperspectral data mining to identify relevant canopy spectral features for estimating durum wheat growth, nitrogen status, and grain yield. Comput. Electron. Agric. 2017, 136, 1–12. [Google Scholar] [CrossRef]
- Pantazi, X.; Moshou, D.; Alexandridis, T.; Whetton, R.; Mouazen, A. Wheat yield prediction using machine learning and advanced sensing techniques. Comput. Electron. Agric. 2016, 121, 57–65. [Google Scholar] [CrossRef]
- Ustin, S.L.; Gitelson, A.A.; Jacquemoud, S.; Schaepman, M.; Asner, G.P.; Gamon, J.A.; Zarco-Tejada, P. Retrieval of foliar information about plant pigment systems from high resolution spectroscopy. Remote Sens. Environ. 2009, 113, 67–77. [Google Scholar] [CrossRef]
- Ceccato, P.; Flasse, S.; Tarantola, S.; Jacquemoud, S.; Grégoire, J.-M. Detecting vegetation leaf water content using reflectance in the optical domain. Remote Sens. Environ. 2001, 77, 22–33. [Google Scholar] [CrossRef]
- Cornelissen, J.H.C.; Lavorel, S.; Garnier, E.; Díaz, S.; Buchmann, N.; Gurvich, D.E.; Reich, P.B.; Ter Steege, H.; Morgan, H.D.; Van Der Heijden, M.G.A.; et al. A handbook of protocols for standardised and easy measurement of plant functional traits worldwide. Aust. J. Bot. 2003, 51, 335–380. [Google Scholar] [CrossRef] [Green Version]
- Thenkabail, P.S.; Gumma, M.K.; Teluguntla, P.; Mohammed, I.A. Hyperspectral remote sensing of vegetation and agricultural crops. Photogramm. Eng. Remote Sens. 2014, 80, 697–723. [Google Scholar]
- Sonobe, R.; Wang, Q. Nondestructive assessments of carotenoids content of broadleaved plant species using hyperspectral indices. Comput. Electron. Agric. 2018, 145, 18–26. [Google Scholar] [CrossRef]
- Haboudane, D. Hyperspectral vegetation indices and novel algorithms for predicting green LAI of crop canopies: Modeling and validation in the context of precision agriculture. Remote Sens. Environ. 2004, 90, 337–352. [Google Scholar] [CrossRef]
- Gitelson, A.A. Wide Dynamic Range Vegetation Index for Remote Quantification of Biophysical Characteristics of Vegetation. J. Plant Physiol. 2004, 161, 165–173. [Google Scholar] [CrossRef]
- Thorp, K.; Gore, M.; Andrade-Sanchez, P.; Carmo-Silva, A.; Welch, S.; White, J.; French, A.; Thorp, K. Proximal hyperspectral sensing and data analysis approaches for field-based plant phenomics. Comput. Electron. Agric. 2015, 118, 225–236. [Google Scholar] [CrossRef] [Green Version]
- Gilbertson, J.K.; Van Niekerk, A. Value of dimensionality reduction for crop differentiation with multi-temporal imagery and machine learning. Comput. Electron. Agric. 2017, 142, 50–58. [Google Scholar] [CrossRef]
- Mountrakis, G.; Im, J.; Ogole, C. Support vector machines in remote sensing: A review. ISPRS J. Photogramm. Sens. 2011, 66, 247–259. [Google Scholar] [CrossRef]
- Verger, A.; Baret, F.; Camacho, F. Optimal modalities for radiative transfer-neural network estimation of canopy biophysical characteristics: Evaluation over an agricultural area with CHRIS/PROBA observations. Remote Sens. Environ. 2011, 115, 415–426. [Google Scholar] [CrossRef]
- Atzberger, C.; Guérif, M.; Baret, F.; Werner, W. Comparative analysis of three chemometric techniques for the spectroradiometric assessment of canopy chlorophyll content in winter wheat. Comput. Electron. Agric. 2010, 73, 165–173. [Google Scholar] [CrossRef]
- Verrelst, J.; Malenovský, Z.; Van Der Tol, C.; Camps-Valls, G.; Gastellu-Etchegorry, J.-P.; Lewis, P.; North, P.; Moreno, J. Quantifying Vegetation Biophysical Variables from Imaging Spectroscopy Data: A Review on Retrieval Methods. Surv. Geophys. 2018, 1–41. [Google Scholar] [CrossRef]
- Baret, F.; Buis, S. Estimating Canopy Characteristics from Remote Sensing Observations: Review of Methods and Associated Problems. In Advances in Land Remote Sensing; Springer Nature: Basingstoke, UK, 2008; pp. 173–201. [Google Scholar]
- Kuester, T.; Spengler, D. Structural and Spectral Analysis of Cereal Canopy Reflectance and Reflectance Anisotropy. Remote Sens. 2018, 10, 1767. [Google Scholar] [CrossRef]
- Disney, M.; Lewis, P.; North, P. Monte Carlo ray tracing in optical canopy reflectance modelling. Sens. Rev. 2000, 18, 163–196. [Google Scholar] [CrossRef]
- Gastellu-Etchegorry, J.; Demarez, V.; Pinel, V.; Zagolski, F. Modeling radiative transfer in heterogeneous 3-D vegetation canopies. Remote Sens. Environ. 1996, 58, 131–156. [Google Scholar] [CrossRef]
- Govaerts, Y.; Verstraete, M. Raytran: A Monte Carlo ray-tracing model to compute light scattering in three-dimensional heterogeneous media. IEEE Trans. Geosci. Sens. 1998, 36, 493–505. [Google Scholar] [CrossRef]
- Jacquemoud, S.; Verhoef, W.; Baret, F.; Bacour, C.; Zarco-Tejada, P.J.; Asner, G.P.; François, C.; Ustin, S.L. Prospect + sail models: A review of use for vegetation characterization. Remote Sens. Environ. 2009, 113 (Suppl. 1), S56–S66. [Google Scholar] [CrossRef]
- Féret, J.-B.; François, C.; Asner, G.P.; Gitelson, A.A.; Martin, R.E.; Bidel, L.P.; Ustin, S.L.; Le Maire, G.; Jacquemoud, S. PROSPECT-4 and 5: Advances in the leaf optical properties model separating photosynthetic pigments. Remote Sens. Environ. 2008, 112, 3030–3043. [Google Scholar] [CrossRef]
- Féret, J.-B.; Gitelson, A.; Noble, S.; Jacquemoud, S. PROSPECT-D: Towards modeling leaf optical properties through a complete lifecycle. Remote Sens. Environ. 2017, 193, 204–215. [Google Scholar] [CrossRef] [Green Version]
- Jacquemoud, S.; Baret, F. PROSPECT: A model of leaf optical properties spectra. Remote Sens. Environ. 1990, 34, 75–91. [Google Scholar] [CrossRef]
- Verhoef, W. Light scattering by leaf layers with application to canopy reflectance modeling: The SAIL model. Remote Sens. Environ. 1984, 16, 125–141. [Google Scholar] [CrossRef] [Green Version]
- Verhoef, W.; Jia, L.; Xiao, Q.; Su, Z. Unified Optical-Thermal Four-Stream Radiative Transfer Theory for Homogeneous Vegetation Canopies. IEEE Trans. Geosci. Sens. 2007, 45, 1808–1822. [Google Scholar] [CrossRef]
- Pu, R. Hyperspectral Remote Sensing: Fundamentals and Practices; CRC Press: Boca Raton, FL, USA, 2017. [Google Scholar]
- Hank, T.B.; Berger, K.; Bach, H.; Clevers, J.G.P.W.; Gitelson, A.; Zarco-Tejada, P.; Mauser, W. Spaceborne Imaging Spectroscopy for Sustainable Agriculture: Contributions and Challenges. Surv. Geophys. 2018, 1–37. [Google Scholar] [CrossRef]
- Guanter, L.; Kaufmann, H.; Segl, K.; Foerster, S.; Rogass, C.; Chabrillat, S.; Kuester, T.; Hollstein, A.; Rossner, G.; Chlebek, C.; et al. The EnMAP Spaceborne Imaging Spectroscopy Mission for Earth Observation. Remote Sens. 2015, 7, 8830–8857. [Google Scholar] [CrossRef] [Green Version]
- Candela, L.; Formaro, R.; Guarini, R.; Loizzo, R.; Longo, F.; Varacalli, G. The prisma mission. In Proceedings of the 2016 IEEE International Geoscience and Remote Sensing Symposium (IGARSS), Beijing, China, 10–15 July 2016; pp. 253–256. [Google Scholar]
- Feingersh, T.; Ben Dor, E. SHALOM—A Commercial Hyperspectral Space Mission; Wiley: Hoboken, NJ, USA, 2015; pp. 247–263. [Google Scholar]
- Lee, C.M.; Cable, M.L.; Hook, S.J.; Green, R.O.; Ustin, S.L.; Mandl, D.J.; Middleton, E.M. An introduction to the nasa hyperspectral infrared imager (hyspiri) mission and preparatory activities. Remote Sens. Environ. 2015, 167, 6–19. [Google Scholar] [CrossRef]
- Nieke, J.; Rast, M. Towards the copernicus hyperspectral imaging mission for the environment (chime). In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 157–159. [Google Scholar]
- Berger, K.; Atzberger, C.; Danner, M.; D’Urso, G.; Mauser, W.; Vuolo, F.; Hank, T. Evaluation of the prosail model capabilities for the future enmap model environment: A review study. Remote Sens. 2017. under review. [Google Scholar]
- Richter, K.; Hank, T.B.; Vuolo, F.; Mauser, W.; D’Urso, G. Optimal Exploitation of the Sentinel-2 Spectral Capabilities for Crop Leaf Area Index Mapping. Remote Sens. 2012, 4, 561–582. [Google Scholar] [CrossRef] [Green Version]
- Danner, M.; Berger, K.; Wocher, M.; Mauser, W.; Hank, T. Retrieval of Biophysical Crop Variables from Multi-Angular Canopy Spectroscopy. Remote Sens. 2017, 9, 726. [Google Scholar] [CrossRef]
- Verrelst, J.; Rivera, J.P.; Leonenko, G.; Alonso, L.; Moreno, J. Optimizing LUT-Based RTM Inversion for Semiautomatic Mapping of Crop Biophysical Parameters from Sentinel-2 and -3 Data: Role of Cost Functions. IEEE Trans. Geosci. Sens. 2014, 52, 257–269. [Google Scholar] [CrossRef]
- Darvishzadeh, R.; Skidmore, A.; Schlerf, M.; Atzberger, C. Inversion of a radiative transfer model for estimating vegetation LAI and chlorophyll in a heterogeneous grassland. Remote Sens. Environ. 2008, 112, 2592–2604. [Google Scholar] [CrossRef]
- Locherer, M.; Hank, T.; Danner, M.; Mauser, W. Retrieval of Seasonal Leaf Area Index from Simulated EnMAP Data through Optimized LUT-Based Inversion of the PROSAIL Model. Remote Sens. 2015, 7, 10321–10346. [Google Scholar] [CrossRef] [Green Version]
- Kimes, D.; Knyazikhin, Y.; Privette, J.; Abuelgasim, A.; Gao, F. Inversion methods for physically-based models. Sens. Rev. 2000, 18, 381–439. [Google Scholar] [CrossRef]
- Rivera, J.P.; Verrelst, J.; Leonenko, G.; Moreno, J. Multiple Cost Functions and Regularization Options for Improved Retrieval of Leaf Chlorophyll Content and LAI through Inversion of the PROSAIL Model. Remote Sens. 2013, 5, 3280–3304. [Google Scholar] [CrossRef] [Green Version]
- Lauvernet, C.; Baret, F.; Hascoët, L.; Buis, S.; Le Dimet, F.-X. Multitemporal-patch ensemble inversion of coupled surface–atmosphere radiative transfer models for land surface characterization. Remote Sens. Environ. 2008, 112, 851–861. [Google Scholar] [CrossRef]
- Atzberger, C. Object-based retrieval of biophysical canopy variables using artificial neural nets and radiative transfer models. Remote Sens. Environ. 2004, 93, 53–67. [Google Scholar] [CrossRef]
- Broge, N.; Leblanc, E. Comparing prediction power and stability of broadband and hyperspectral vegetation indices for estimation of green leaf area index and canopy chlorophyll density. Remote Sens. Environ. 2001, 76, 156–172. [Google Scholar] [CrossRef]
- Weiss, M.; Baret, F.; Myneni, R.B.; Pragnère, A.; Knyazikhin, Y. Investigation of a model inversion technique to estimate canopy biophysical variables from spectral and directional reflectance data. Agronomie 2000, 20, 3–22. [Google Scholar] [CrossRef]
- Berger, K.; Atzberger, C.; Danner, M.; Wocher, M.; Mauser, W.; Hank, T. Model-Based Optimization of Spectral Sampling for the Retrieval of Crop Variables with the PROSAIL Model. Remote Sens. 2018, 10, 2063. [Google Scholar] [CrossRef]
- Atzberger, C.; Darvishzadeh, R.; Schlerf, M.; Le Maire, G. Suitability and adaptation of PROSAIL radiative transfer model for hyperspectral grassland studies. Sens. Lett. 2013, 4, 55–64. [Google Scholar] [CrossRef]
- ASDInc. Fieldspec 3 User Manual. 2010. Available online: http://www.Geo-informatie.Nl/courses/grs60312/material2017/manuals/600540-jfieldspec3usermanual.pdf (accessed on 5 May 2019).
- Danner, M.; Locherer, M.; Hank, T.; Richter, K. Enmap Field Guides Technical Report—Spectral Sampling with The Asd Fieldspec 4. 2015. Available online: http://gfzpublic.gfz-potsdam.de/pubman/faces/viewItemOverviewPage.jsp?itemId=escidoc:1388298 (accessed on 5 May 2019). [CrossRef]
- Savitzky, A.; Golay, M.J.E. Smoothing and Differentiation of Data by Simplified Least Squares Procedures. Anal. Chem. 1964, 36, 1627–1639. [Google Scholar] [CrossRef]
- Suunto. Suunto Precision Instruments User Guide. 2017. Available online: https://ns.Suunto.Com/manuals/pm-5/userguides/suunto_precisioninstruments_qg_de.Pdf?_ga=2.98826141.267561439.1552297146-115087547.1552297146 (accessed on 5 May 2019).
- Campbell, G. Extinction coefficients for radiation in plant canopies calculated using an ellipsoidal inclination angle distribution. Agric. Meteorol. 1986, 36, 317–321. [Google Scholar] [CrossRef]
- Danner, M.; Locherer, M.; Hank, T.; Richter, K. Enmap Field Guides Technical Report—Measuring leaf area index (lai) with the li-cor lai 2200c or lai-2200 (+ 2200clear kit). 2015. Available online: http://gfzpublic.gfz-potsdam.de/pubman/faces/viewItemOverviewPage.jsp?itemId=escidoc:1381850(accessed on 5 May 2019). [CrossRef]
- LICOR-Biosciences. Lai-2200c plant canopy analyzer instruction manual. Available online: https://licor.app.boxenterprise.net/s/fqjn5mlu8c1a7zir5qel (accessed on 11 May 2019).
- Jay, S.; Bendoula, R.; Hadoux, X.; Féret, J.-B.; Gorretta, N. A physically-based model for retrieving foliar biochemistry and leaf orientation using close-range imaging spectroscopy. Remote Sens. Environ. 2016, 177, 220–236. [Google Scholar] [CrossRef]
- Baret, F.; Hagolle, O.; Geiger, B.; Bicheron, P.; Miras, B.; Huc, M.; Berthelot, B.; Niño, F.; Weiss, M.; Samain, O.; et al. Lai, fapar and fcover cyclopes global products derived from vegetation: Part 1: Principles of the algorithm. Remote Sens. Environ. 2007, 110, 275–286. [Google Scholar] [CrossRef]
- Jiang, J.; Comar, A.; Burger, P.; Bancal, P.; Weiss, M.; Baret, F. Estimation of leaf traits from reflectance measurements: Comparison between methods based on vegetation indices and several versions of the PROSPECT model. Plant Methods 2018, 14, 23. [Google Scholar] [CrossRef]
- Suess, A.; Danner, M.; Obster, C.; Locherer, M.; Hank, T.; Richter, K. Enmap Field Guides Technical Report—Measuring Leaf Chlorophyll Content with The Konica Minolta Spad-502plus. 2015. Available online: http://gfzpublic.gfz-potsdam.de/pubman/faces/viewItemFullPage.jsp?itemId=escidoc%3A1388302%3A2&view=EXPORT (accessed on 5 May 2019). [CrossRef]
- Lichtenthaler, H.K. Chlorophylls and carotenoids: Pigments of photosynthetic biomembranes. Methods Enzymol. 1987, 148, 350–382. [Google Scholar]
- Baret, F.; Andrieu, B.; Guyot, G. A Simple Model for Leaf Optical Properties in Visible and Near-Infrared: Application to the Analysis of Spectral Shifts Determinism. In Applications of Chlorophyll Fluorescence in Photosynthesis Research, Stress Physiology, Hydrobiology and Remote Sensing; Springer Nature: Basingstoke, UK, 1988; pp. 345–351. [Google Scholar]
- Bleiholder, H.; Weber, E.; Lancashire, P.; Feller, C.; Buhr, L.; Hess, M.; Wicke, H.; Hack, H.; Meier, U.; Klose, R. Growth stages of mono-and dicotyledonous plants, bbch monograph. In Federal Biological Research Centre for Agriculture and Forestry, Berlin/Braunschweig, Germany; Meier, U., Ed.; GFAR: Vienna, Austria, 2001; p. 158. [Google Scholar]
- Zadoks, J.C.; Chang, T.T.; Konzak, C.F. A decimal code for the growth stages of cereals. Weed Res. 1974, 14, 415–421. [Google Scholar] [CrossRef]
- Van Der Walt, S.; Colbert, S.C.; Varoquaux, G. The NumPy Array: A Structure for Efficient Numerical Computation. Comput. Sci. Eng. 2011, 13, 22–30. [Google Scholar] [CrossRef] [Green Version]
- Danner, M.; Wocher, M.; Berger, K.; Mauser, W.; Hank, T. Developing a Sandbox Environment for Prosail, Suitable for Education and Research. In Proceedings of the GARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 783–786. [Google Scholar]
- Rabe, A.; Jakimow, B.; Thiel, F.; Hostert, P.; van der Linden, S. Enmap-box 3 a free and open source python plug-in for qgis. In Proceedings of the IGARSS 2018-2018 IEEE International Geoscience and Remote Sensing Symposium, Valencia, Spain, 22–27 July 2018; pp. 7764–7766. [Google Scholar]
- François, C.; Ottle, C.; Olioso, A.; Prévot, L.; Bruguier, N.; Ducros, Y. Conversion of 400-1100 nm vegetation albedo measurements into total shortwave broadband albedo using a canopy radiative transfer model. Agronomie 2002, 22, 611–618. [Google Scholar] [CrossRef]
- Cannavò, F. Sensitivity analysis for volcanic source modeling quality assessment and model selection. Comput. Geosci. 2012, 44, 52–59. [Google Scholar] [CrossRef]
- Lillesaeter, O. Spectral reflectance of partly transmitting leaves: Laboratory measurements and mathematical modeling. Remote Sens. Environ. 1982, 12, 247–254. [Google Scholar] [CrossRef]
- A Sims, D.; A Gamon, J. Estimation of vegetation water content and photosynthetic tissue area from spectral reflectance: a comparison of indices based on liquid water and chlorophyll absorption features. Remote Sens. Environ. 2003, 84, 526–537. [Google Scholar] [CrossRef]
- Bull, C. Wavelength selection for near-infrared reflectance moisture meters. J. Agric. Eng. 1991, 49, 113–125. [Google Scholar] [CrossRef]
- Van Der Walt, S.; Schonberger, J.L.; Nunez-Iglesias, J.; Boulogne, F.; Warner, J.D.; Yager, N.; Gouillart, E.; Yu, T.; Gomez, S. scikit-image: image processing in Python. PeerJ 2014, 2, 453. [Google Scholar] [CrossRef]
- Richter, K.; Atzberger, C.; Hank, T.B.; Mauser, W. Derivation of biophysical variables from Earth observation data: Validation and statistical measures. J. Appl. Sens. 2012, 6, 63557. [Google Scholar] [CrossRef]
- Datt, B. Remote Sensing of Water Content in Eucalyptus Leaves. Aust. J. Bot. 1999, 47, 909. [Google Scholar] [CrossRef]
- Suits, G. The calculation of the directional reflectance of a vegetative canopy. Remote Sens. Environ. 1971, 2, 117–125. [Google Scholar] [CrossRef]
- Knipling, E.B. Physical and physiological basis for the reflectance of visible and near-infrared radiation from vegetation. Remote Sens. Environ. 1970, 1, 155–159. [Google Scholar] [CrossRef]
- Carter, G.A. Primary and Secondary Effects of Water Content on the Spectral Reflectance of Leaves. Am. J. Bot. 1991, 78, 916. [Google Scholar] [CrossRef]
- Verhoef, W.; Bach, H. Coupled soil–leaf-canopy and atmosphere radiative transfer modeling to simulate hyperspectral multi-angular surface reflectance and TOA radiance data. Remote Sens. Environ. 2007, 109, 166–182. [Google Scholar] [CrossRef]
- Casa, R.; Baret, F.; Buis, S.; López-Lozano, R.; Pascucci, S.; Palombo, A.; Jones, H.G.; Jones, H. Estimation of maize canopy properties from remote sensing by inversion of 1-D and 4-D models. Precis. Agric. 2010, 11, 319–334. [Google Scholar] [CrossRef] [Green Version]
- Botha, E.J.; LeBlon, B.; Zebarth, B.J.; Watmough, J. Non-destructive estimation of wheat leaf chlorophyll content from hyperspectral measurements through analytical model inversion. Int. J. Sens. 2010, 31, 1679–1697. [Google Scholar] [CrossRef]
- Tripathi, R.; Sahoo, R.N.; Sehgal, V.K.; Tomar, R.K.; Chakraborty, D.; Nagarajan, S. Inversion of prosail model for retrieval of plant biophysical parameters. J. Indian Soc. Remote Sens. 2012, 40, 19–28. [Google Scholar] [CrossRef]
- Zou, X.; Mõttus, M. Retrieving crop leaf tilt angle from imaging spectroscopy data. Agric. Meteorol. 2015, 205, 73–82. [Google Scholar] [CrossRef]
- Zou, X.; Mõttus, M. Sensitivity of Common Vegetation Indices to the Canopy Structure of Field Crops. Remote Sens. 2017, 9, 994. [Google Scholar] [CrossRef]
- Atzberger, C.; Richter, K. Spatially constrained inversion of radiative transfer models for improved LAI mapping from future Sentinel-2 imagery. Remote Sens. Environ. 2012, 120, 208–218. [Google Scholar] [CrossRef]
- Laurent, V.C.; Verhoef, W.; Clevers, J.G.; Schaepman, M.E. Inversion of a coupled canopy–atmosphere model using multi-angular top-of-atmosphere radiance data: A forest case study. Remote Sens. Environ. 2011, 115, 2603–2612. [Google Scholar] [CrossRef]
- Clevers, J.; Kooistra, L.; Schaepman, M.; Clevers, J.; Schaepman, M. Estimating canopy water content using hyperspectral remote sensing data. Int. J. Appl. Earth Obs. Geoinf. 2010, 12, 119–125. [Google Scholar] [CrossRef]
- Jacquemoud, S. Comparison of Four Radiative Transfer Models to Simulate Plant Canopies Reflectance Direct and Inverse Mode. Remote Sens. Environ. 2000, 74, 471–481. [Google Scholar] [CrossRef]
- Newnham, G.; Burt, T. Validation of a leaf reflectance and transmittance model for three agricultural crop species. In Proceedings of the IGARSS’01 IEEE 2001 International Geoscience and Remote Sensing Symposium, Sydney, Australia, 9–13 July 2001; pp. 2976–2978. [Google Scholar]
- Baret, F.; Fourty, T. Estimation of leaf water content and specific leaf weight from reflectance and transmittance measurements. Agronomie 1997, 17, 455–464. [Google Scholar] [CrossRef] [Green Version]
- Jacquemoud, S.; Ustin, S. In Application of radiative transfer models to moisture content estimation and burned land mapping. In Proceedings of the 4th International Workshop on Remote Sensing and GIS Applications to Forest Fire Management, Ghent, Belgium, 5–7 June 2003. [Google Scholar]
- Wocher, M.; Berger, K.; Danner, M.; Mauser, W.; Hank, T. Physically-Based Retrieval of Canopy Equivalent Water Thickness Using Hyperspectral Data. Remote Sens. 2018, 10, 1924. [Google Scholar] [CrossRef]
- Huber, K.; Dorigo, W.; Bauer, T.; Eitzinger, S.; Haumann, J.; Kaiser, G.; Linke, R.; Postl, W.; Rischbeck, P.; Schneider, W. Changes in spectral reflectance of crop canopies due to drought stress. In Proceedings of the Remote Sensing for Agriculture, Ecosystems, and Hydrology VII, Bruges, Belgium, 19 October 2005; International Society for Optics and Photonics: Washington, DC, USA, 2005; p. 59761I. [Google Scholar]
- Landi, M.; Tattini, M.; Gould, K.S. Multiple functional roles of anthocyanins in plant-environment interactions. Environ. Exp. Bot. 2015, 119, 4–17. [Google Scholar] [CrossRef]
- Wang, W.-M.; Li, Z.-L.; Su, H.-B. Comparison of leaf angle distribution functions: Effects on extinction coefficient and fraction of sunlit foliage. Agric. Meteorol. 2007, 143, 106–122. [Google Scholar] [CrossRef] [Green Version]
- Ali, A.M.; Darvishzadeh, R.; Skidmore, A.K.; Van Duren, I.; Heiden, U.; Heurich, M. Estimating leaf functional traits by inversion of PROSPECT: Assessing leaf dry matter content and specific leaf area in mixed mountainous forest. Int. J. Appl. Earth Obs. Geoinf. 2016, 45, 66–76. [Google Scholar] [CrossRef]
- Wang, L.; Qu, J.J.; Hao, X.; Hunt, E.R., Jr. Estimating dry matter content from spectral reflectance for green leaves of different species. Int. J. Remote Sens. 2011, 32, 7097–7109. [Google Scholar] [CrossRef]
- Casas, A.; Riano, D.; Ustin, S.; Dennison, P.; Salas, J. Estimation of water-related biochemical and biophysical vegetation properties using multitemporal airborne hyperspectral data and its comparison to MODIS spectral response. Remote Sens. Environ. 2014, 148, 28–41. [Google Scholar] [CrossRef]
- Dong, T.; Wu, B.; Meng, J.; Du, X.; Shang, J. Sensitivity analysis of retrieving fraction of absorbed photosynthetically active radiation (FPAR) using remote sensing data. Acta Ecol. Sin. 2016, 36, 1–7. [Google Scholar] [CrossRef]
- Jonckheere, I.; Fleck, S.; Nackaerts, K.; Muys, B.; Coppin, P.; Weiss, M.; Baret, F. Review of methods for in situ leaf area index determination: Part i. Theories, sensors and hemispherical photography. Agric. For. Meteorol. 2004, 121, 19–35. [Google Scholar] [CrossRef]
- Si, Y.; Schlerf, M.; Zurita-Milla, R.; Skidmore, A.; Wang, T. Mapping spatio-temporal variation of grassland quantity and quality using MERIS data and the PROSAIL model. Remote Sens. Environ. 2012, 121, 415–425. [Google Scholar] [CrossRef]
- Claverie, M.; Vermote, E.F.; Weiss, M.; Baret, F.; Hagolle, O.; Demarez, V. Validation of coarse spatial resolution LAI and FAPAR time series over cropland in southwest France. Remote Sens. Environ. 2013, 139, 216–230. [Google Scholar] [CrossRef]














| Parameter | Description | Unit | Model Versions |
|---|---|---|---|
| N | Leaf structure parameter | - | Prospect (all) |
| Ccab | Leaf Chlorophylla+b content | µg cm−2 | Prospect (all) |
| Cw | Leaf Equivalent Water Thickness (EWT) | cm | Prospect (all) |
| Cm | Leaf Mass per Area | g cm−2 | Prospect (all) |
| Ccar | Leaf Carotenoids content | μg cm−2 | Prospect 5 |
| Cbrown | Leaf Brown Pigments parameter | - | Prospect 5b |
| Canth | Leaf Anthocyanins content | μg cm−2 | Prospect D |
| LAI | Leaf Area Index | m2 m−2 | 4SAIL |
| LIDF or ALIA | Leaf Inclination Distribution Function or Average Leaf Inclination Angle | - or Deg | 4SAIL |
| Hspot | Hot Spot size parameter | - | 4SAIL |
| ρsoil | Soil Reflectance | - | 4SAIL |
| Psoil | Soil Brightness Parameter | - | 4SAIL |
| SZA | Sun Zenith Angle | Deg | 4SAIL |
| OZA | Observer Zenith Angle | Deg | 4SAIL |
| rAA | relative Azimuth Angle | Deg | 4SAIL |
| skyl | Ratio of diffuse to total incident radiation | - | 4SAIL |
| Year | Crop | No. of Field Dates |
|---|---|---|
| 2014 | Winter wheat | 10 |
| 2014 | Silage maize | 11 |
| 2015 | Winter wheat | 11 |
| 2017 | Winter wheat | 12 |
| 2017 | Silage maize | 8 |
| 2018 | Winter wheat | 7 |
| 2018 | Silage maize | 7 |
| Winter wheat | Silage Maize | ||||||
|---|---|---|---|---|---|---|---|
| Variable | Year | Range | Mean | Std. | Range | Mean | Std. |
| LAI (-) | 2014 | 0.08–6.27 | 4.82 | 1.85 | 0.09–4.03 | 2.21 | 1.58 |
| 2015 | 0.33–6.20 | 2.82 | 2.10 | ||||
| 2017 | 0.76–6.20 | 4.34 | 1.79 | 0.21–3.86 | 2.29 | 1.28 | |
| 2018 | 0.01–5.98 | 3.88 | 1.98 | 1.79–3.61 | 3.05 | 0.60 | |
| ALIA (deg) | 2014 | 25–75 | 52 | 19 | 36–75 | 50 | 11 |
| 2015 | 35–77 | 60 | 13 | ||||
| 2017 | 45–78 | 68 | 9 | 49–71 | 63 | 8 | |
| 2018 | 45–76 | 64 | 10 | 49–75 | 59 | 8 | |
| Ccab (µg cm−2) | 2014 | 13.4–49.1 | 42.7 | 10.5 | 27.3–61.8 | 48.1 | 11.9 |
| 2015 | 14.3–53.3 | 43.2 | 12.8 | ||||
| 2017 | 18.2–59.5 | 50.0 | 10.7 | 38.4–55.2 | 48.8 | 5.6 | |
| 2018 | 11.6–53.2 | 43.2 | 14.3 | 48.2–60.8 | 56.8 | 4.1 | |
| Cbrown (-) | 2014 | 0.0–0.98 | 0.19 | 0.30 | 0.0–0.81 | 0.08 | 0.23 |
| 2015 | 0.0–0.90 | 0.22 | 0.34 | ||||
| 2017 | 0.0–0.80 | 0.09 | 0.22 | 0.0–0.05 | 0.01 | 0.02 | |
| 2018 | 0.0–1.0 | 0.18 | 0.37 | 0.0–0.01 | <0.00 | <0.00 | |
| EWT (cm) | 2014 | 0.012–0.035 | 0.027 | 0.006 | 0.011–0.031 | 0.027 | 0.005 |
| 2015 | 0.008–0.034 | 0.026 | 0.007 | ||||
| 2017 | 0.003–0.020 | 0.015 | 0.004 | 0.012–0.021 | 0.016 | 0.003 | |
| 2018 | 0.001–0.019 | 0.013 | 0.006 | 0.020–0.025 | 0.023 | 0.002 | |
| Cm (g cm−2) | 2014 | 0.0047–0.0075 | 0.0063 | 0.0010 | 0.0032–0.0056 | 0.0046 | 0.0007 |
| 2015 | 0.0036–0.0061 | 0.0046 | 0.0007 | ||||
| 2017 | 0.0031–0.0059 | 0.0047 | 0.0008 | 0.0027–0.0049 | 0.0040 | 0.0007 | |
| 2018 | 0.0043–0.0066 | 0.0049 | 0.0008 | 0.0045–0.0070 | 0.0058 | 0.0008 | |
| BBCH-Code | Associated Macro Stage |
|---|---|
| 0 | Germination / sprouting / bud development |
| 1 | Leaf development |
| 2 * | Tillering / Formation of side shoots |
| 3 | Stem elongation or rosette growth / shoot development |
| 4 * | Development of harvestable vegetative plant parts / booting |
| 5 | Inflorescence emergence / heading |
| 6 | Flowering |
| 7 | Development of fruit |
| 8 | Ripening or maturity of fruit and seed |
| 9 | Senescence, beginning of dormancy |
| Variable | Season | RMSE | rRMSE | R2 |
|---|---|---|---|---|
| ALIA | 2014 | 18.2° | 0.34 | 0.12 |
| 2015 | 12.3° | 0.20 | 0.02 | |
| 2017 | 7.7° | 0.12 | 0.47 | |
| 2018 | 12.6° | 0.19 | 0.77 | |
| All | 12.9° | 0.21 | 0.18 | |
| EWT | 2014 | 0.025 cm | 0.87 | 0.65 |
| 2015 | 0.027 cm | 0.96 | 0.37 | |
| 2017 | 0.027 cm | 1.8 | 0.16 | |
| 2018 | 0.021 cm | 1.26 | 0.47 | |
| All | 0.026 cm | 1.18 | 0.02 | |
| Cbrown | 2014 | 0.21 | 2.10 | 0.99 |
| 2015 | 0.11 | 1.33 | 0.69 | |
| 2017 | 0.13 | 1.48 | 0.96 | |
| 2018 | 0.12 | 14.1 | 0.57 | |
| All | 0.15 | 1.94 | 0.79 |
| Variable | Season | RMSE | rRMSE | R2 |
|---|---|---|---|---|
| ALIA | 2014 | 13.1° | 0.27 | 0.44 |
| 2017 | 19.4° | 0.30 | 0.06 | |
| 2018 | 16.0° | 0.27 | 0.30 | |
| All | 16.1° | 0.28 | 0.04 | |
| EWT | 2014 | 0.008 cm | 0.30 | 0.19 |
| 2017 | 0.010 cm | 0.64 | 0.25 | |
| 2018 | 0.019 cm | 0.83 | 0.62 | |
| All | 0.013 cm | 0.58 | 0.01 | |
| Cbrown | 2014 | 0.11 | 14.16 | 0.32 |
| 2017 | 0.09 | 12.37 | 0.76 | |
| 2018 | 0.15 | 101.58 | 0.30 | |
| All | 0.12 | 20.58 | 0.24 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Danner, M.; Berger, K.; Wocher, M.; Mauser, W.; Hank, T. Fitted PROSAIL Parameterization of Leaf Inclinations, Water Content and Brown Pigment Content for Winter Wheat and Maize Canopies. Remote Sens. 2019, 11, 1150. https://doi.org/10.3390/rs11101150
Danner M, Berger K, Wocher M, Mauser W, Hank T. Fitted PROSAIL Parameterization of Leaf Inclinations, Water Content and Brown Pigment Content for Winter Wheat and Maize Canopies. Remote Sensing. 2019; 11(10):1150. https://doi.org/10.3390/rs11101150
Chicago/Turabian StyleDanner, Martin, Katja Berger, Matthias Wocher, Wolfram Mauser, and Tobias Hank. 2019. "Fitted PROSAIL Parameterization of Leaf Inclinations, Water Content and Brown Pigment Content for Winter Wheat and Maize Canopies" Remote Sensing 11, no. 10: 1150. https://doi.org/10.3390/rs11101150
APA StyleDanner, M., Berger, K., Wocher, M., Mauser, W., & Hank, T. (2019). Fitted PROSAIL Parameterization of Leaf Inclinations, Water Content and Brown Pigment Content for Winter Wheat and Maize Canopies. Remote Sensing, 11(10), 1150. https://doi.org/10.3390/rs11101150