Quantitative Assessment of the Impact of Physical and Anthropogenic Factors on Vegetation Spatial-Temporal Variation in Northern Tibet
Abstract
:1. Introduction
2. Materials and Methods
2.1. Study Area
2.2. Datasets
2.2.1. NDVI Time Series
2.2.2. Physical Factors Influencing Vegetation Variation
2.2.3. Anthropogenic Factors Influencing Vegetation Variation
2.3. Analysis
2.3.1. Mann Kendall (MK) Test
2.3.2. Trend Analysis
2.3.3. Geographical Detector Model
2.3.4. Discretization Method
3. Results
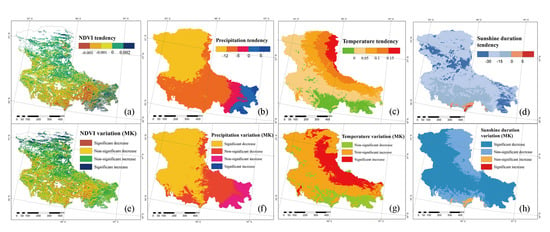
3.1. Trend and Trend Shift Analysis of NDVI and Environment Factors in Northern Tibet
3.2. Assessing the Impact of Individual Factors on Vegetation Variation
3.3. Interaction between Factors That Influence Vegetation Variation
3.4. Identification of Areas Vulnerable to Vegetation Degradation
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
Appendix A
| Discretization Methods | Factors | q Values | ||||||
|---|---|---|---|---|---|---|---|---|
| 2 | 3 | 4 | 5 | 6 | 7 | 8 | ||
| EI | Temperature | 0.0585 | 0.1400 | 0.0612 | 0.1753 | 0.1677 | 0.1418 | 0.1677 |
| NB | 0.1245 | 0.1663 | 0.1550 | 0.1632 | 0.1826 | 0.1849 | 0.1831 | |
| QU | 0.1562 | 0.1448 | 0.1649 | 0.1833 | 0.1782 | 0.1839 | 0.1867 | |
| GI | 0.1625 | 0.1559 | 0.1382 | 0.1247 | 0.1900 | 0.1729 | 0.2019 | |
| SD | - | - | - | - | 0.1705 | - | - | |
| EI | Precipitation | 0.4816 | 0.4600 | 0.5277 | 0.5097 | 0.5578 | 0.5447 | 0.5608 |
| NB | 0.4752 | 0.4650 | 0.5260 | 0.5564 | 0.5528 | 0.5655 | 0.5580 | |
| QU | 0.2805 | 0.4363 | 0.5134 | 0.5261 | 0.5324 | 0.5478 | 0.5678 | |
| GI | 0.3053 | 0.4606 | 0.4853 | 0.5333 | 0.5403 | 0.5460 | 0.5680 | |
| SD | - | - | - | - | 0.5498 | - | - | |
| EI | Elevation | 0.0494 | 0.0686 | 0.0618 | 0.1038 | 0.1078 | 0.1118 | 0.1634 |
| NB | 0.0486 | 0.0865 | 0.0957 | 0.1791 | 0.1569 | 0.1582 | 0.1485 | |
| QU | 0.0501 | 0.0756 | 0.0891 | 0.0983 | 0.1015 | 0.1106 | 0.1082 | |
| GI | 0.0494 | 0.0657 | 0.0886 | 0.0867 | 0.0989 | 0.1382 | 0.1276 | |
| SD | - | - | - | - | 0.1594 | - | - | |
| EI | Slope | 0.0048 | 0.0676 | 0.0750 | 0.0990 | 0.0989 | 0.1092 | 0.1146 |
| NB | 0.0795 | 0.1017 | 0.1067 | 0.1189 | 0.1226 | 0.1161 | 0.1231 | |
| QU | 0.0494 | 0.0709 | 0.0931 | 0.0942 | 0.1063 | 0.1095 | 0.1089 | |
| GI | 0.0493 | 0.0884 | 0.0982 | 0.1160 | 0.1042 | 0.1067 | 0.1107 | |
| SD | - | - | 0.1100 | - | - | - | 0.1193 | |
| EI | Roads density | 0.1471 | 0.1407 | 0.1904 | 0.2186 | 0.2305 | 0.2427 | 0.2500 |
| NB | 0.1186 | 0.1943 | 0.2575 | 0.2566 | 0.2672 | 0.2733 | 0.2781 | |
| QU | 0.1294 | 0.1603 | 0.1676 | 0.1856 | 0.1975 | 0.2164 | 0.2252 | |
| GI | 0.1414 | 0.1707 | 0.1777 | 0.2706 | 0.2682 | 0.2679 | 0.2737 | |
| SD | - | - | 0.2345 | - | - | - | 0.2758 | |
| EI | Residential density | 0.0404 | 0.0633 | 0.0768 | 0.1198 | 0.1493 | 0.1929 | 0.2380 |
| NB | 0.0698 | 0.3401 | 0.3736 | 0.3795 | 0.4296 | 0.4405 | 0.4346 | |
| QU | 0.1962 | 0.3357 | 0.4026 | 0.4438 | 0.4484 | 0.4393 | 0.4568 | |
| GI | 0.1884 | 0.3412 | 0.3828 | 0.3820 | 0.4411 | 0.4470 | 0.4377 | |
| SD | - | - | 0.3215 | - | - | 0.4441 | ||
| EI | Sunshine duration | 0.2508 | 0.2373 | 0.2842 | 0.3910 | 0.3861 | 0.4229 | 0.4365 |
| NB | 0.1922 | 0.3571 | 0.4385 | 0.4607 | 0.4657 | 0.4956 | 0.4790 | |
| QU | 0.1651 | 0.2925 | 0.3651 | 0.3835 | 0.4212 | 0.4314 | 0.4722 | |
| GI | 0.1293 | 0.3707 | 0.4204 | 0.4304 | 0.4575 | 0.4478 | 0.4821 | |
| SD | - | - | - | - | 0.4677 | |||
| EI | Grazing density | 0.3368 | 0.4621 | 0.5313 | 0.5626 | 0.5670 | 0.5810 | 0.6085 |
| NB | 0.4587 | 0.5092 | 0.5825 | 0.6069 | 0.6075 | 0.6077 | 0.6089 | |
| QU | 0.3836 | 0.5174 | 0.5187 | 0.6412 | 0.5898 | 0.6281 | 0.6278 | |
| GI | 0.3836 | 0.4583 | 0.5448 | 0.5944 | 0.5952 | 0.5559 | 0.5949 | |
| SD | - | - | - | 0.5770 | - | 0.6088 | - | |
| EI | Population density | 0.3309 | 0.4300 | 0.5448 | 0.5445 | 0.5454 | 0.5449 | 0.5779 |
| NB | 0.4274 | 0.5409 | 0.5414 | 0.6194 | 0.6218 | 0.6227 | 0.6227 | |
| QU | 0.3753 | 0.5022 | 0.5030 | 0.6349 | 0.5767 | 0.6296 | 0.6332 | |
| GI | 0.2217 | 0.3758 | 0.5293 | 0.5297 | 0.6210 | 0.6327 | 0.6327 | |
| SD | - | - | 0.6163 | - | - | 0.6356 | - | |
| EI | Per Capita GDP | 0.1170 | 0.1683 | 0.1237 | 0.1392 | 0.2074 | 0.2587 | 0.2009 |
| NB | 0.1170 | 0.1693 | 0.1760 | 0.2074 | 0.3520 | 0.3527 | 0.3884 | |
| QU | 0.0900 | 0.0649 | 0.0902 | 0.2068 | 0.2900 | 0.3047 | 0.3548 | |
| GI | 0.1827 | 0.1219 | 0.1441 | 0.1837 | 0.2009 | 0.1613 | 0.2725 | |
| SD | - | - | - | - | - | 0.1486 | - | |

References
- Zavaleta, E.S.; Shaw, M.R.; Chiariello, N.R.; Mooney, H.A.; Field, C.B. Additive effects of simulated climate changes, elevated CO2, and nitrogen deposition on grassland diversity. Proc. Natl. Acad. Sci. USA 2003, 100, 7650–7654. [Google Scholar] [CrossRef]
- Xu, X.K.; Hong, C.; Levy, J.K. Spatiotemporal vegetation cover variations in the Qinghai-Tibet Plateau under global climate change. Chin. Sci. Bull. 2008, 53, 915–922. [Google Scholar] [CrossRef]
- Chengqun, Y.; Zhang, Y.; Claus, H.; Zeng, R.; Zhang, X.; Wang, J. Ecological and environmental issues faced by a developing Tibet. Environ. Sci. Technol. 2012, 46, 1979. [Google Scholar]
- Leroux, L.; Béguéb, A.; Lo Seen, D.; Jolivotb, A.; Kayitakirec, F. Driving forces of recent vegetation changes in the Sahel: Lessons learned from regional and local level analyses. Remote Sens. Environ. 2017, 191, 38–54. [Google Scholar] [CrossRef]
- Gao, Q.Z.; Wan, Y.F.; Li, Y.; Qin, X.B.; Jiangcun, W.; Xu, X.M. Spatial and temporal pattern of alpine grassland condition and its response to human activities in Northern Tibet, China. Rangel. J. 2010, 32, 165–173. [Google Scholar] [CrossRef]
- Nan, Z. The grassland farming system and sustainable agricultural development in China. Grassl. Sci. 2005, 51, 15–19. [Google Scholar] [CrossRef]
- Harris, R.B. Rangeland degradation on the Qinghai-Tibetan plateau: A review of the evidence of its magnitude and causes. J. Arid Environ. 2010, 74, 1–12. [Google Scholar] [CrossRef]
- Li, X.L.; Gao, J.; Brierley, G.; Qiao, Y.-M.; Zhang, J.; Yang, Y.-W. Rangeland degradation on the Qinghai-Tibet Plateau: Implications for rehabilitation. Land Degrad. Dev. 2013, 24, 72–80. [Google Scholar] [CrossRef]
- Wang, Z.Q.; Zhang, Y.; Yang, Y.; Zhou, W.; Gang, C.; Zhang, Y.; Li, J.; An, R.; Wang, K.; Odeh, I.; et al. Quantitative assess the driving forces on the grassland degradation in the Qinghai-Tibet Plateau, in China. Ecol. Inform. 2016, 33, 32–44. [Google Scholar] [CrossRef]
- Huang, K.; Zhang, Y.; Zhu, J.; Liu, Y.; Zu, J.; Zhang, J. The influences of climate change and human activities on vegetation dynamics in the Qinghai-Tibet Plateau. Remote Sens. 2016, 8, 876. [Google Scholar] [CrossRef]
- Ji, L.; Peters, A.J. Lag and Seasonality Considerations in Evaluating AVHRR NDVI Response to Precipitation. Photogramm. Eng. Remote Sens. 2005, 71, 1053–1061. [Google Scholar] [CrossRef]
- Schultz, P.A.; Halpert, M.S. Global correlation of temperature, NDVI and precipitation. Adv. Space Res. 1993, 13, 277–280. [Google Scholar] [CrossRef]
- Gómez-Mendoza, L.; Galicia, L.; Cuevas-Fernández, M.L.; Magaña, V.; Gómez, G.; Palacio-Prieto, J.L. Assessing onset and length of greening period in six vegetation types in Oaxaca, Mexico, using NDVI-precipitation relationships. Int. J. Biometeorol. 2008, 52, 511–520. [Google Scholar] [CrossRef] [PubMed]
- Xia, Z.; Hu, H.; Shen, H.; Zhou, D.; Zhou, L.; Myneni, R.B.; Fang, J. Satellite-indicated long-term vegetation changes and their drivers on the Mongolian Plateau. Landsc. Ecol. 2015, 30, 1599–1611. [Google Scholar]
- Shen, M.; Piao, S.; Jeong, S.-J.; Zhou, L.; Zeng, Z.; Ciais, P.; Chen, D.; Huang, M.; Jin, C.-S.; Li, L.Z.X.; et al. Evaporative cooling over the Tibetan Plateau induced by vegetation growth. Proc. Natl. Acad. Sci. USA 2015, 112, 9299–9304. [Google Scholar] [CrossRef] [PubMed] [Green Version]
- Jian, S.; Qin, X.; Yang, J. The response of vegetation dynamics of the different alpine grassland types to temperature and precipitation on the Tibetan Plateau. Environ. Monit. Assess. 2016, 188, 1–11. [Google Scholar]
- Sun, J.; Cheng, G.; Li, W.; Sha, Y.; Yang, Y. On the variation of NDVI with the principal climatic elements in the Tibetan Plateau. Remote Sens. 2013, 5, 1894–1911. [Google Scholar] [CrossRef]
- Chu, D.; Lu, L.; Zhang, T. Sensitivity of normalized difference vegetation index (NDVI) to seasonal and interannual climate conditions in the Lhasa area, Tibetan Plateau, China. Arct. Antarct. Alp. Res. 2007, 39, 635–641. [Google Scholar] [CrossRef]
- Shen, Z.; Fu, G.; Yu, C.; Sun, W.; Zhang, X. Relationship between the growing season maximum enhanced vegetation index and climatic factors on the Tibetan Plateau. Remote Sens. 2014, 6, 6765–6789. [Google Scholar] [CrossRef]
- Dardel, C.; Kergoat, L.; Hiernaux, P.; Mougin, E.; Grippa, M.; Tucker, C.J. Re-greening Sahel: 30 years of remote sensing data and field observations (Mali, Niger). Remote Sens. Environ. 2014, 140, 350–364. [Google Scholar] [CrossRef]
- Piao, S.; Fang, J.; He, J. Variations in vegetation net primary production in the Qinghai-Xizang Plateau, China, from 1982 to 1999. Clim. Change 2006, 74, 253–267. [Google Scholar] [CrossRef]
- Gao, Q.; Li, Y.; Wan, Y.; Qin, X.; Jiangcun, W.; Liu, Y. Dynamics of alpine grassland NPP and its response to climate change in Northern Tibet. Clim. Chang. 2009, 97, 515. [Google Scholar] [CrossRef]
- Liu, L.; Yili, Z.; Wanqi, B.; Jianzhong, Y.; Mingjun, D.; Zhenxi, S.; Shuangcheng, L.; Du, Z. Characteristics of grassland degradation and driving forces in the source region of the Yellow River from 1985 to 2000. J. Geogr. Sci. 2006, 16, 131–142. [Google Scholar] [CrossRef]
- Fassnacht, F.E.; Li, L.; Fritz, A. Mapping degraded grassland on the Eastern Tibetan Plateau with multi-temporal Landsat 8 data—Where do the severely degraded areas occur? Int. J. Appl. Earth Obs. Geoinf. 2015, 42, 115–127. [Google Scholar] [CrossRef]
- Zhang, Y.; Liu, L.; Yili, Z.; Wanqi, B.; Jianzhong, Y.; Mingjun, D.; Zhenxi, S.; Shuangcheng, L.; Du, Z. Grassland degradation in the source region of the Yellow River. Acta Geogr. Sin. 2006, 61, 3–14. [Google Scholar]
- Hui, Z.; Ning, K.N.; Shu Juan, L.I. Human impacts on landscape structure in Wolong Natural Reserve. Acta Ecol. Sin. 2001, 21, 1994–2001. [Google Scholar]
- Evans, J.; Geerken, R. Discrimination between climate and human-induced dryland degradation. J. Arid Environ. 2004, 57, 535–554. [Google Scholar] [CrossRef]
- Fang, X.; Zhu, Q.; Chen, H.; Ma, Z.; Wang, W.; Song, X.; Zhao, P.; Peng, C. Analysis of vegetation dynamics and climatic variability impacts on greenness across Canada using remotely sensed data from 2000 to 2009. J. Appl. Remote Sens. 2014, 8, 243–247. [Google Scholar] [CrossRef]
- Zhou, X.Y.; Shi, H.D.; Wang, X.R. Impact of climate change and human activities on vegetation coverage in the Mongolian Plateau. Arid Zone Res. 2014, 31, 604–610. [Google Scholar]
- Song, C.Q.; SongCai, Y.; GaoHuan, L.; LingHong, K.; XinKe, Z. Spatio-temporal pattern and change of Nagqu grassland and the influence of human factors. Acta Prat. Sin. 2012, 21, 1–10. [Google Scholar]
- Wang, J.F.; Li, X.-H.; Christakos, G.; Liao, Y.-L.; Zhang, T.; Gu, X.; Zheng, X.-Y. Geographical detectors-based health risk assessment and its application in the neural tube defects study of the Heshun region, China. Int. J. Geogr. Inf. Sci. 2010, 24, 107–127. [Google Scholar] [CrossRef]
- Wang, J.; Xu, C. Geodetector: Principle and prospective. Acta Geogr. Sin. 2017, 72, 116–134. [Google Scholar]
- Liang, P.; Yang, X. Landscape spatial patterns in the Maowusu (Mu Us) Sandy Land, northern China and their impact factors. CATENA 2016, 145, 321–333. [Google Scholar] [CrossRef]
- Du, Z.; Xu, X.; Zhang, H.; Wu, Z.; Liu, Y. Geographical detector-based identification of the impact of major determinants on aeolian desertification risk. PLoS ONE 2016, 11, e0151331. [Google Scholar] [CrossRef] [PubMed]
- Wang, J.F.; Hu, Y. Environmental health risk detection with GeogDetector. Environ. Model. Softw. 2005, 33, 114–115. [Google Scholar] [CrossRef]
- Liu, S.Z.; Zhou, L.; Qiu, C.S.; Zhang, J.P.; Fang, Y.P.; Gao, W.S. Studies on Grassland Degradation and Desertification of Naqu Prefecture in Tibet Autonomous Region; The Tibet People’s Publishing House: Lhasa, China, 1999. [Google Scholar]
- Zhang, X.; Lu, X.; Wang, X. Spatial-temporal NDVI variation of different alpine grassland classes and groups in Northern Tibet from 2000 to 2013. Mt. Res. Dev. 2015, 35, 254–263. [Google Scholar] [CrossRef]
- Didan, K. MOD13Q1 MODIS/Terra Vegetation Indices 16-Day L3 Global 250m SIN Grid V006 [Data set]; NASA EOSDIS LP DAAC: Sioux Falls, SD, USA, 2015. [Google Scholar]
- Stow, D.; Hope, P.A.; Engstrom, R.; Coulter, L. Greenness trends of Arctic tundra vegetation in the 1990s: comparison of two NDVI data sets from NOAA AVHRR systems. Int. J. Remote Sens. 2007, 28, 4807–4822. [Google Scholar] [CrossRef]
- Yang, Y.H.; Shi-Long, P. Variations in grassland vegetation cover in relation to climatic factors on the Tibetan Plateau. J. Plant Ecol. 2006, 30, 1–8. [Google Scholar]
- Hutchinson, M.F. Interpolating mean rainfall using thin plate smoothing splines. Int. J. Geogr. Inf. Syst. 1995, 9, 385–403. [Google Scholar] [CrossRef] [Green Version]
- Lehnert, L.W.; Wesche, K.; Trachte, K.; Reudenbach, C.; Bendix, J. Climate variability rather than overstocking causes recent large scale cover changes of Tibetan pastures. Sci. Rep. 2016, 6, 24367. [Google Scholar] [CrossRef] [Green Version]
- Sneyers, R. On the Statistical Analysis of Series of Observations; World Meteorological Organization: Geneva, Switzerland, 1990. [Google Scholar]
- Sneyers, R. Sur la Determination de la Stabilite des Series Climatologiques. In Changes of Climate: Proceedings of the Rome Symposium/Organized by Unesco and the World Meteorological Organization; Unesco: Paris, France, 1963. [Google Scholar]
- Sayemuzzaman, M.; Jha, M. Seasonal and annual precipitation time series trend analysis in North Carolina, United States. Atmos. Res. 2014, 137, 183–194. [Google Scholar] [CrossRef]
- Chen, Z.; Chen, D.; Xie, X.; Cai, J.; Zhuang, Y.; Cheng, N.; He, B.; Gao, B. Spatial self-aggregation effects and national division of city-level PM2.5 concentrations in China based on spatio-temporal clustering. J. Clean. Prod. 2019, 207, 875–881. [Google Scholar] [CrossRef]
- Jiao, K.; Gao, J.; Wu, S. Climatic determinants impacting the distribution of greenness in China: regional differentiation and spatial variability. Int. J. Biometeorol. 2019, 63, 523–533. [Google Scholar] [CrossRef]
- Luo, L.; Mei, K.; Qu, L.; Zhang, C.; Chen, H.; Wang, S.; Di, D.; Huang, H.; Wang, Z.; Xia, F.; et al. Assessment of the Geographical Detector Method for investigating heavy metal source apportionment in an urban watershed of Eastern China. Sci. Total Environ. 2019, 653, 714–722. [Google Scholar] [CrossRef] [PubMed]
- Xu, C.; Zhang, X.; Xiao, G. Spatiotemporal decomposition and risk determinants of hand, foot and mouth disease in Henan, China. Sci. Total Environ. 2019, 657, 509–516. [Google Scholar] [CrossRef]
- Cao, F.; Ge, Y.; Wang, J. Optimal discretization for geographical detectors-based risk assessment. Mapp. Sci. Remote Sens. 2013, 50, 78–92. [Google Scholar] [CrossRef]
- Li, Z.; Guo, H.; Ji, L.; Lei, L.; Wang, C.; Yan, D.; Li, B.; Li, J. Vegetation greenness trend (2000 to 2009) and the climate controls in the Qinghai-Tibetan Plateau. J. Appl. Remote Sens. 2013, 7, 3572. [Google Scholar]
- Sun, Y.L.; Zhou, C.P.; Shi, P.L.; Song, M.H.; Xiong, D.P. The variability of grassland net primary production in Tibet and its responses to no grazing project. Chin. J. Grassl. 2014, 36, 5–12. [Google Scholar]
- Yan, G.J.; Hu, R.; Luo, J.; Weiss, M.; Jiang, H.; Mu, X.; Xie, D.; Zhang, W. Review of indirect optical measurements of leaf area index: Recent advances, challenges, and perspectives. Agric. For. Meteorol. 2019, 265, 390–411. [Google Scholar] [CrossRef]
- Hu, R.; Yan, G.; Mu, X.; Luo, J. Indirect measurement of leaf area index on the basis of path length distribution. Remote Sens. Environ. 2014, 155, 239–247. [Google Scholar] [CrossRef]
- Zhang, J.; Yao, F.; Zheng, L.; Yang, L. Evaluation of grassland dynamics in the Northern-Tibet Plateau of China using remote sensing and climate data. Sensors 2007, 7, 3312–3328. [Google Scholar] [CrossRef]
- Ding, M.J.; Zhang, Y.; Liu, L.; Wang, Z.; Yang, X. Seasonal time lag response of NDVI to temperature and precipitation change and its spatial characteristics in Tibetan Plateau. Prog. Geogr. 2010, 29, 507–512. [Google Scholar]
- Sun, J.; Cheng, G.W.; Li, W.P. Meta-analysis of relationships between environmental factors and aboveground biomass in the alpine grassland on the Tibetan Plateau. Biogeosciences 2013, 10, 1707–1715. [Google Scholar] [CrossRef]
- Fu, G.; Shen, Z.X.; Zhang, X.Z. Increased precipitation has stronger effects on plant production of an alpine meadow than does experimental warming in the Northern Tibetan Plateau. Agric. For. Meteorol. 2018, 249, 79–86. [Google Scholar] [CrossRef]
- Cui, Q.H.; Jiang, Z.-G.; Liu, J.-K.; Su, J.-P. A review of the cause of rangeland degradation on Qinghai-Tibet Plateau. Pratac. Sci. 2007, 24, 20–26. [Google Scholar]
- Fang, J.; Piao, S.; Tang, Z.; Peng, C.; Ji, W.; Knapp, A.K.; Smith, M.D. Interannual variability in net primary production and precipitation. Science 2001, 293, 1723. [Google Scholar] [CrossRef] [PubMed]
- Guo, Y.; Gong, P.; Amundson, R.; Yu, Q. Analysis of factors controlling soil carbon in the conterminous United States. Soil Sci. Soc. Am. J. 2006, 70, 601–612. [Google Scholar] [CrossRef]
- Li, J.; Shen, Z.; Li, C.; Kou, Y.; Wang, Y.; Tu, B.; Zhang, Z.; Li, X. Stair-step pattern of soil bacterial diversity mainly driven by pH and vegetation types along the elevational gradients of Gongga Mountain, China. Front. Microbiol. 2018, 9, 569. [Google Scholar] [CrossRef]
- Zhang, G.Q.; Zhu, J.-J.; Li, R.-P.; Li, X.-F. Estimation of photosynthetically active radiation (PAR) using sunshine duration. Chin. J. Ecol. 2015, 34, 3560–3567. [Google Scholar]
- Li, Z.; Moreau, L.; Cihlar, J. Estimation of photosynthetically active radiation absorbed at the surface. J. Geophys. Res. Atmos. 1997, 102, 29717–29727. [Google Scholar] [CrossRef] [Green Version]








| Interaction | Judgment Criteria |
|---|---|
| Enhance | q(X1∩X2) > q(X1) or q(X2) |
| Enhance, bivariate | q(X1∩X2) > q(X1) and q(X2) |
| Enhance, nonlinear | q(X1∩X2) > q(X1) + q(X2) |
| Weaken | q(X1∩X2) < q(X1) + q(X2) |
| Weaken, univariate | q(X1∩X2) < q(X1) or q(X2) |
| Weaken, nonlinear | q(X1∩X2) < q(X1) and q(X2) |
| Independent | q(X1∩X2) = q(X1) + q(X2) |
| Grassland Type | Influencing Factors | |||||
|---|---|---|---|---|---|---|
| Meadow | Precipitation | Grazing density | Population density | Temperature | Per capita GDP | Slope |
| q | 0.282 ** | 0.205 ** | 0.201 ** | 0.165 ** | 0.157 ** | 0.141 ** |
| Scrub | Population density | Grazing density | Per capita GDP | Precipitation | Residential density | Temperature |
| q | 0.101 ** | 0.096 ** | 0.087 ** | 0.076 ** | 0.074 ** | 0.058 ** |
| Steppe | Temperature | Population density | Per capita GDP | Grazing density | Slope | Road density |
| q | 0.118 ** | 0.115 ** | 0.112 ** | 0.101 ** | 0.072 ** | 0.055 ** |
| Alpine Meadow | Alpine Scrub | Alpine Steppe | |
|---|---|---|---|
| 1st | Precipitation ∩ Temperature | Temperature ∩ GDP | Soil ∩ Population |
| q | 0.446 | 0.275 | 0.294 |
| 2nd | Precipitation ∩ Elevation | Sunshine ∩ GDP | Soil ∩ GDP |
| q | 0.443 | 0.271 | 0.289 |
| 3rd | Precipitation ∩ Sunshine | Sunshine ∩ Population | Soil ∩ Temperature |
| q | 0.416 | 0.262 | 0.288 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Ran, Q.; Hao, Y.; Xia, A.; Liu, W.; Hu, R.; Cui, X.; Xue, K.; Song, X.; Xu, C.; Ding, B.; et al. Quantitative Assessment of the Impact of Physical and Anthropogenic Factors on Vegetation Spatial-Temporal Variation in Northern Tibet. Remote Sens. 2019, 11, 1183. https://doi.org/10.3390/rs11101183
Ran Q, Hao Y, Xia A, Liu W, Hu R, Cui X, Xue K, Song X, Xu C, Ding B, et al. Quantitative Assessment of the Impact of Physical and Anthropogenic Factors on Vegetation Spatial-Temporal Variation in Northern Tibet. Remote Sensing. 2019; 11(10):1183. https://doi.org/10.3390/rs11101183
Chicago/Turabian StyleRan, Qinwei, Yanbin Hao, Anquan Xia, Wenjun Liu, Ronghai Hu, Xiaoyong Cui, Kai Xue, Xiaoning Song, Cong Xu, Boyang Ding, and et al. 2019. "Quantitative Assessment of the Impact of Physical and Anthropogenic Factors on Vegetation Spatial-Temporal Variation in Northern Tibet" Remote Sensing 11, no. 10: 1183. https://doi.org/10.3390/rs11101183
APA StyleRan, Q., Hao, Y., Xia, A., Liu, W., Hu, R., Cui, X., Xue, K., Song, X., Xu, C., Ding, B., & Wang, Y. (2019). Quantitative Assessment of the Impact of Physical and Anthropogenic Factors on Vegetation Spatial-Temporal Variation in Northern Tibet. Remote Sensing, 11(10), 1183. https://doi.org/10.3390/rs11101183