Speckle Noise Reduction Technique for SAR Images Using Statistical Characteristics of Speckle Noise and Discrete Wavelet Transform
Abstract
:1. Introduction
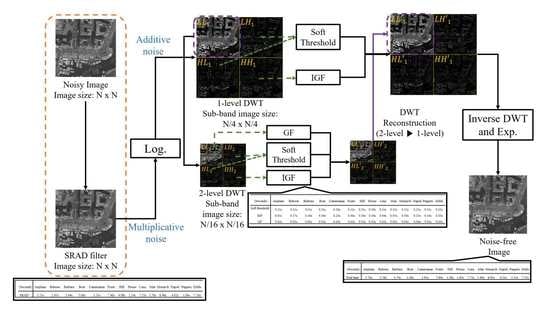
2. Proposed Algorithm
2.1. Speckle Reducing Anisotropic Diffusion
2.2. Logarithmic Transformation
2.3. Discrete Wavelet Transform
2.4. Soft Threshold
2.5. Guided Filter
2.6. Improved Guided Filter
2.6.1. A New Edge-Aware Weighting
2.6.2. The Proposed Filter
2.7. Evaluation Metrics
3. Experimental Results
3.1. Experiments on Standard Images
3.2. Experiments on Real SAR Images
3.3. Computational Complexity
4. Discussion
5. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Yahya, N.; Karmel, N.S.; Malik, A.S. Subspace-Based Technique for Speckle Noise Reduction in SAR Images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6257–6271. [Google Scholar] [CrossRef]
- Liu, F.; Wu, J.; Li, L.; Jiao, L.; Hao, H.; Zhang, X. A Hybrid Method of SAR Speckle Reduction Based on Geometric-Structural Block and Adaptive Neighborhood. IEEE Trans. Geosci. Remote Sens. 2018, 56, 730–747. [Google Scholar] [CrossRef]
- Guo, F.; Zhang, G.; Zhang, Q.; Zhao, R.; Deng, M.; Xu, K. Speckle Suppression by Weighted Euclidean Distance Anisotropic Diffusion. Remote Sens. 2018, 10, 722. [Google Scholar] [CrossRef]
- Yuan, Q.; Zhang, Q.; Li, J.; Shen, H.; Zhang, L. Hyperspectral image denoising employing a spatial-spectral deep residual convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1205–1218. [Google Scholar] [CrossRef]
- Zhang, Q.; Yuan, Q.; Zeng, C.; Wei, X.; Wei, Y. Missing data reconstruction in remote sensing image with a unified spatial-temporal-spectral deep convolutional neural network. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4274–4288. [Google Scholar] [CrossRef]
- Yuan, Y.; Fang, J.; Lu, X.; Feng, Y. Remote sensing image scene classification using rearranged local features. IEEE Trans. Geosci. Remote Sens. 2018, 57, 1779–1792. [Google Scholar] [CrossRef]
- Tu, B.; Zhang, X.; Kang, X.; Zhang, G.; Li, S. Density peak-based noisy label detection for hyperspectral image classification. IEEE Trans. Geosci. Remote Sens. 2019, 57, 1573–1584. [Google Scholar] [CrossRef]
- Gemme, L.; Dellepiane, S.G. An automatic data-driven method for SAR image segmentation in sea surface analysis. IEEE Trans. Geosci. Remote Sens. 2018, 56, 2633–2646. [Google Scholar] [CrossRef]
- Duan, Y.; Liu, F.; Jiao, L.; Tao, X.; Wu, J.; Shi, C.; Wimmers, M.O. Adaptive hierarchical multinomial latent model with hybrid kernel function for SAR image semantic segmentation. IEEE Trans. Geosci. Remote Sens. 2018, 56, 5997–6015. [Google Scholar] [CrossRef]
- Liu, S.; Wu, G.; Zhang, X.; Zhang, K.; Wang, P.; Li, Y. SAR despeckling via classification-based nonlocal and local sparse representation. Neurocomputing 2017, 219, 174–185. [Google Scholar] [CrossRef]
- Xie, H.; Pierce, L.E.; Ulaby, F.T. Statistical properties of logarithmically transformed speckle. IEEE Trans. Geosci. Remote Sens. 2002, 40, 721–727. [Google Scholar] [CrossRef]
- Barash, D. A fundamental relationship between bilateral filtering, adaptive smoothing and the nonlinear diffusion equation. IEEE Trans. Pattern Anal. Machine Intell. 2002, 24, 844–867. [Google Scholar] [CrossRef]
- Tomasi, C.; Manduchi, R. Bilateral Filtering for Gray and Color Images. In Proceedings of the Sixth International Conference on Computer Vision, Bombay, India, 4–7 January 1998; pp. 839–846. [Google Scholar]
- Buades, A.; Coll, B.; Morel, J.-M. A non-local algorithm for image denoising. In Proceedings of the 2005 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, San Diego, CA, USA, 20–25 June 2005; pp. 60–65. [Google Scholar]
- Buades, A.; Coll, B.; Morel, J.M. A review of image denoising algorithms, with a new one. SIAM Multiscale Model. Simul. 2005, 490–530. [Google Scholar] [CrossRef]
- Torres, L.; Sant’Anna, S.J.S.; Freitas, C.D.C.; Frery, C. Speckle reduction in polarimetric SAR imagery with stochastic distances and nonlocal means. Pattern Recognit. 2014, 141–157. [Google Scholar] [CrossRef]
- Xu, W.; Tang, C.; Gu, F.; Cheng, J. Combination of oriented partial differential equation and shearlet transform for denoising in electronic speckle pattern interferometry fringe patters. Appl. Opt. 2017, 56, 2843–2850. [Google Scholar] [CrossRef] [PubMed]
- Perona, P.; Malik, J. Scale-Space and Edge Detection Using Anisotropic Diffusion. IEEE Trans. Pattern Anal. Mach. Intell. 1990, 12, 629–639. [Google Scholar] [CrossRef]
- Li, J.C.; Ma, Z.H.; Peng, Y.X.; Huang, H. Speckle reduction by image entropy anisotropic diffusion. Acta Phys. Sin. 2013, 62, 099501. [Google Scholar]
- Deledalle, C.A.; Denis, L.; Tupin, F. Iterative weighted maximum likelihood denoising with probabilistic patch-based weights. IEEE Trans. Image Process. 2009, 18, 2661–2672. [Google Scholar] [CrossRef]
- Zhang, J.; Lin, G.; Wu, L.; Cheng, Y. Speckle filtering of medical ultrasonic images using wavelet and guided filter. Ultrasonics 2016, 65, 177–193. [Google Scholar] [CrossRef] [PubMed]
- Su, X.; Deledalle, C.; Tupin, F.; Sun, F. Two-step multitemporal nonlocal means for synthetic aperture radar images. IEEE Trans. Geosci. Remote Sens. 2014, 52, 6181–6196. [Google Scholar]
- Chierchia, C.; Mirelle, E.G.; Scarpa, G.; Verdoliva, L. Multitemporal SAR image despeckling based on block-matching and collaborative filtering. IEEE Trans. Geosci. Remote Sens. 2017, 55, 5467–5480. [Google Scholar] [CrossRef]
- Parrilli, S.; Poderico, M.; Angelino, C.V.; Verdoliva, L. A nonlocal SAR image denoising algorithm based on LLMMSE wavelet shrinkage. IEEE Trans. Geosci. Remote Sens. 2012, 50, 606–616. [Google Scholar] [CrossRef]
- Wu, M.-T. Wavelet transform based on Meyer algorithm for image edge and blocking artifact reduction. Inf. Sci. 2019, 474, 125–135. [Google Scholar] [CrossRef]
- Singh, R.; Khare, A. Fusion of multimodal medical images using Daubechies complex wavelet transform—A multiresolution approach. Inform. Fusion 2014, 19, 49–60. [Google Scholar] [CrossRef]
- Li, H.; Manjunath, B.S.; Mitra, S.K. Multisensor image fusion using the wavelet transform. Graph. Models Image Process. 1995, 57, 235–245. [Google Scholar] [CrossRef]
- Pajares, G.; de la Cruz, J.M. A wavelet-based image fusion tutorial. Pattern Recognit. 2004, 37, 1855–1872. [Google Scholar] [CrossRef]
- Huang, Z.-H.; Li, W.-J.; Wang, J.; Zhang, T. Face recognition based on pixel-level and feature-level fusion of the top-level’s wavelet sub-bands. Inf. Fusion 2015, 22, 95–104. [Google Scholar] [CrossRef]
- Hsia, C.-H.; Guo, J.-M. Efficient modified directional lifting-based discrete wavelet transform for moving object detection. Signal Process. 2014, 96, 138–152. [Google Scholar] [CrossRef]
- Liu, S.; Florencio, D.; Li, W.; Zhao, Y.; Cook, C. A Fusion Framework for Camouflaged Moving Foreground Detection in the Wavelet Domain. IEEE Trans. Image Process. 2018, 27, 3918–3930. [Google Scholar] [CrossRef]
- Donoho, D.L. De-noising by soft-thresholding. IEEE Trans. Inf. Theory 1995, 25, 613–627. [Google Scholar] [CrossRef]
- Donoho, D.L.; Johnstone, I.M. Adapting to unknown smoothness via wavelet shrinkage. J. Am. Stat. Assoc. 1995, 90, 1200–1224. [Google Scholar] [CrossRef]
- Chang, S.G.; Yu, B.; Vetterli, M. Adaptive wavelet thresholding for image denoising and compression. IEEE Trans. Image Process. 2000, 9, 1532–1546. [Google Scholar] [CrossRef] [Green Version]
- Yang, Y.; Ding, Z.; Liu, J.; Gao, Q.; Yuan, X.; Lu, X. An adaptive SAR image speckle noise algorithm based on wavelet transform and diffusion equations for marine scenes. In Proceedings of the 2017 IEEE International Geoscience and Remote Sensing Symposium, Fort Worth, TX, USA, 23–28 July 2017; pp. 1–4. [Google Scholar]
- Amini, M.; Ahmad, M.O.; Swamy, M.N.S. SAR image despeckling using vector-based hidden markov model in wavelet domain. In Proceedings of the 2016 IEEE Canadian Conference on Electrical and Computer Engineering, Vancouver, BC, Canada, 15–18 May 2016; pp. 1–4. [Google Scholar]
- Li, H.-C.; Hong, W.H.; Wu, Y.-R.; Fan, P.-Z. Bayesian Wavelet Shrinkage with Heterogeneity-Adaptive Threshold for SAR images despeckling based on Generalized Gamma Distribution. IEEE Trans. Geosci. Remote Sens. 2013, 51, 2388–2402. [Google Scholar] [CrossRef]
- Rajesh, M.R.; Mridula, S.; Mohanan, P. Speckle Noise Reduction in Images using Wiener Filtering and Adaptive Wavelet Thresholding. In Proceedings of the 2016 IEEE Region 10 Conference (TENCON), Singapore, 22–25 November 2016; pp. 2860–2863. [Google Scholar]
- Yu, Y.; Acton, S.T. Speckle reducing anisotropic diffusion. IEEE Trans. Image Process. 2002, 11, 1260–1270. [Google Scholar] [PubMed] [Green Version]
- Dass, R. Speckle noise reduction of ultrasound images using BFO cascaded with wiener filter and discrete wavelet transform in homomorphic region. Procedia Comput. Sci. 2018, 132, 1543–1551. [Google Scholar] [CrossRef]
- Singh, P.; Shree, R. A new SAR image despeckling using directional smoothing filter and method noise thresholding. Eng. Sci. Technol. Int. J. 2019, 21, 589–610. [Google Scholar] [CrossRef]
- Choi, H.H.; Lee, J.H.; Kim, S.M.; Park, S.Y. Speckle noise reduction in ultrasound images using a discrete wavelet transform-based image fusion technique. Biomed. Mater. Eng. 2015, 26, 1587–1597. [Google Scholar] [CrossRef] [PubMed]
- Gao, F.; Xue, X.; Sun, J.; Wang, J.; Zhang, Y. A SAR Image Despeckling Method Based on Two-Dimensional S Transform Shrinkage. IEEE Trans. Geosci. Remote Sens. 2016, 54, 3025–3034. [Google Scholar] [CrossRef]
- Sivaranjania, R.; Roomi, S.M.M.; Senthilarasi, M. Speckle noise removal in SAR images using Multi-Objective PSO (MOPSO) algorithm. Appl. Soft Comput. 2019, 76, 671–681. [Google Scholar] [CrossRef]
- He, K.; Sun, J.; Tang, X. Guided image filtering. IEEE Trans. Pattern Anal. Mach. Intell. 2013, 35, 1397–1409. [Google Scholar] [CrossRef]
- Saevarsson, B.B.; Sveinsson, J.R.; Benediktsson, J.A. Combined Wavelet and Curvelet Denoising of SAR Images. In Proceedings of the 2007 IEEE International Geoscience and Remote Sensing Symposium, Barcelona, Spain, 23–28 July 2007; pp. 4235–4238. [Google Scholar]
- Zhang, M.; Gunturk, B.K. Multiresolution Bilateral Filtering for Image Denoising. IEEE Trans. Image Process. 2008, 17, 2324–2333. [Google Scholar] [CrossRef] [Green Version]
- Sheikh, H.R.; Bovik, A.C.; Cormack, L. No-reference Quality Assessment Using Natural Scene Statistics: JPEG2000. IEEE Trans. Image Process. 2005, 14, 1918–1927. [Google Scholar] [CrossRef] [PubMed]
- Wenxuan, S.; Jie, L.; Minyuan, W. An image denoising method based on multiscale wavelet thresholding and bilateral filtering. Wuhan Univ. J. Nat. Sci. 2010, 15, 148–152. [Google Scholar]
- Frost, V.S.; Stiles, J.A.; Shanmugan, K.S.; Holtzman, J.C. A model for radar images and its application to adaptive digital filtering of multiplicative noise. IEEE Trans. Pattern Anal. Mach. Intell. 1982, PAMI-4, 66–157. [Google Scholar] [CrossRef]
- Lee, S.T. Digital image enhancement and noise filtering by use of local statistics. IEEE Trans. Pattern Anal. Mach. Intell. 1980, PAMI-2, 165–168. [Google Scholar] [CrossRef]
- Treece, G. The bitonic filter: Linear filtering in an edge-preserving morphological framework. IEEE Trans. Image Process. 2016, 25, 5199–5211. [Google Scholar] [CrossRef] [PubMed]
- Farbman, Z.; Fattal, R.; Lischinski, D.; Szeliski, R. Edge-preserving decomposition for multi-scale tone and detail manipulation. ACM Trans. Graph. 2008, 27. [Google Scholar] [CrossRef]
- Zhu, L.; Fu, C.-W.; Brown, M.S.; Heng, P.-A. A non-local low-rank framework for ultrasound speckle reduction. In Proceedings of the 2017 IEEE Conference on Computer Vision and Pattern Recognition, Honolulu, HI, USA, 21–26 July 2017; pp. 5650–5658. [Google Scholar]
- Ramos-Llordén, G.; Vegas-Sánchez-Ferrero, G.; Martin-Fernández, M.; Alberola-López, C.; Aja-Fernández, S. Anisotropic diffusion filter with memory based on speckle statistics for ultrasound images. IEEE Trans. Image Process. 2015, 24, 345–358. [Google Scholar] [CrossRef]
- Hyunho, C.; Jechang, J. Speckle noise reduction in ultrasound images using SRAD and guided filter. In Proceedings of the International Workshop on Advanced Image Technology, Chiang Mai, Thailand, 7–9 January 2018; pp. 1–4. [Google Scholar]
- Jet Propulsion Laboratory. Available online: https://photojournal.jpl.nasa.gov/catalog/PIA01763 (accessed on 30 December 2018).
- Dataset of Standard 512X512 Grayscale Test Images. Available online: http://decsai.ugr.es/cvg/CG/base.htm (accessed on 30 December 2018).
- Crow, F. Summed-area tables for texture mapping. In Proceedings of the 11th Annual Conference on Computer Graphics and Interactive Techniques, New York, NY, USA, 1984; pp. 207–212. [Google Scholar]
- Elad, M.; Ahalon, M. Image denoising via learned dictionaries and sparse representation. In Proceedings of the 2006 IEEE Computer Society Conference on Computer Vision and Pattern Recognition, New York, NY, USA, 17–22 June 2006; pp. 895–900. [Google Scholar]








| Methods | Optimal Parameters |
|---|---|
| NLM | Mask size = 3 × 3 |
| Frost | Mask size = 3 × 3 |
| Lee | Mask size = 3 × 3 |
| Bitonic | Mask size = 3 × 3 |
| WLS | Mask size = 3 × 3, = 3 |
| NLLR | = 10, H = 10 |
| ADMSS | = 0.5, = 0.1, = 15 |
| SAR-BM3D | Number of rows/cols of block = 9, Maximum size of the 3rd dimension of a stack = 16, Diameter of search area = 39, Dimension of step = 3, Parameter of the 2D Kaiser window = 2, Transform UDWT = daub4 |
| SRAD Filter | IGF | GF | |
|---|---|---|---|
| Airplane | Time step = 0.01 Exponential decay rate = 1 Number of iterations = 115 | Mask size = 33 × 33 Regularization parameter = 0.0001 | Mask size = 3 × 3 Regularization parameter = 0.001 |
| Baboon | Time step = 0.01 Exponential decay rate = 1 Number of iterations = 50 | Mask size = 5 × 5 Regularization parameter = 1e−10 | Mask size = 3 × 3 Regularization parameter = 0.001 |
| Barbara | Time step = 0.01 Exponential decay rate = 1 Number of iterations = 70 | Mask size = 3 × 3 Regularization parameter = 1e−10 | Mask size = 3 × 3 Regularization parameter = 0.001 |
| Boat | Time step = 0.01 Exponential decay rate = 1 Number of iterations = 100 | Mask size = 3 × 3 Regularization parameter = 1e−10 | Mask size = 3 × 3 Regularization parameter = 0.001 |
| Cameraman | Time step = 0.01 Exponential decay rate = 1 Number of iterations = 200 | Mask size = 3 × 3 Regularization parameter = 1e−10 | Mask size = 3 × 3 Regularization parameter = 0.001 |
| Fruits | Time step = 0.01 Exponential decay rate = 1 Number of iterations = 150 | Mask size = 17 × 17 Regularization parameter = 0.01 | Mask size = 3 × 3 Regularization parameter = 0.001 |
| Hill | Time step = 0.01 Exponential decay rate = 1 Number of iterations = 100 | Mask size = 17 × 17 Regularization parameter = 1e−10 | Mask size = 3 × 3 Regularization parameter = 0.001 |
| House | Time step = 0.01 Exponential decay rate = 1 Number of iterations = 190 | Mask size = 3 × 3 Regularization parameter = 1e−10 | Mask size = 3 × 3 Regularization parameter = 0.001 |
| Lena | Time step = 0.01 Exponential decay rate = 1 Number of iterations = 150 | Mask size = 17 × 17 Regularization parameter = 0.01 | Mask size = 3 × 3 Regularization parameter = 0.001 |
| Man | Time step = 0.01 Exponential decay rate = 1 Number of iterations = 100 | Mask size = 17 × 17 Regularization parameter = 0.01 | Mask size = 3 × 3 Regularization parameter = 0.001 |
| Monarch | Time step = 0.01 Exponential decay rate = 1 Number of iterations = 100 | Mask size = 3 × 3 Regularization parameter = 1e−10 | Mask size = 3 × 3 Regularization parameter = 0.001 |
| Napoli | Time step = 0.01 Exponential decay rate = 1 Number of iterations = 80 | Mask size = 3 × 3 Regularization parameter = 1e−10 | Mask size = 3 × 3 Regularization parameter = 0.001 |
| Peppers | Time step = 0.01 Exponential decay rate = 1 Number of iterations = 120 | Mask size = 3 × 3 Regularization parameter = 1e−10 | Mask size = 3 × 3 Regularization parameter = 0.001 |
| Zelda | Time step = 0.01 Exponential decay rate = 1 Number of iterations = 140 | Mask size = 3 × 3 Regularization parameter = 1e−10 | Mask size = 3 × 3 Regularization parameter = 0.001 |
| Noisy | NLM | Guided | Frost | Lee | Bitonic | WLS | NLLR | ADMSS | SRAD | SRAD-Guided | SAR-BM3D | Proposed | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Airplane | 16.53 | 19.12 | 19.14 | 22.06 | 23.78 | 26.18 | 24.97 | 17.39 | 23.43 | 26.97 | 26.53 | 28.10 | 27.45 |
| Baboon | 18.49 | 21.13 | 21.09 | 21.08 | 21.91 | 21.97 | 22.12 | 19.53 | 18.28 | 23.52 | 22.07 | 22.51 | 22.92 |
| Barbara | 19.16 | 22.40 | 22.05 | 22.34 | 23.26 | 23.68 | 23.78 | 20.39 | 20.50 | 24.99 | 23.75 | 28.32 | 24.59 |
| Boat | 18.46 | 21.81 | 21.68 | 23.36 | 19.41 | 26.39 | 25.50 | 19.65 | 20.14 | 27.37 | 26.59 | 27.20 | 27.55 |
| Camera-man | 18.66 | 21.65 | 21.59 | 22.41 | 22.85 | 24.43 | 25.03 | 19.75 | 17.59 | 26.73 | 24.71 | 26.35 | 26.87 |
| Fruits | 17.08 | 19.96 | 19.98 | 22.30 | 24.08 | 26.33 | 26.31 | 18.04 | 22.07 | 27.45 | 26.93 | 27.68 | 27.45 |
| Hill | 19.79 | 23.54 | 23.38 | 24.64 | 25.48 | 27.58 | 26.75 | 21.26 | 24.92 | 28.25 | 27.82 | 28.30 | 28.27 |
| House | 17.93 | 21.16 | 21.02 | 23.26 | 25.06 | 27.38 | 25.93 | 19.09 | 22.46 | 27.58 | 27.81 | 29.83 | 28.58 |
| Lena | 18.84 | 22.45 | 22.31 | 24.29 | 25.88 | 28.54 | 27.39 | 20.11 | 21.88 | 29.69 | 28.99 | 29.91 | 30.13 |
| Man | 19.51 | 23.07 | 22.94 | 24.41 | 26.15 | 27.46 | 26.46 | 20.83 | 20.82 | 28.31 | 27.68 | 27.71 | 28.55 |
| Monarch | 20.19 | 24.55 | 24.10 | 25.11 | 26.76 | 27.70 | 25.87 | 21.99 | 24.00 | 29.50 | 28.03 | 29.54 | 29.64 |
| Napoli | 21.00 | 24.62 | 24.27 | 24.06 | 24.48 | 24.34 | 23.69 | 22.71 | 22.90 | 26.41 | 24.34 | 25.14 | 25.70 |
| Peppers | 18.74 | 22.05 | 21.79 | 23.50 | 22.92 | 26.62 | 25.77 | 19.96 | 18.13 | 28.29 | 27.22 | 27.13 | 28.44 |
| Zelda | 21.18 | 26.23 | 25.94 | 26.71 | 28.62 | 31.40 | 30.66 | 23.19 | 29.28 | 32.67 | 32.20 | 32.38 | 32.77 |
| Noisy | NLM | Guided | Frost | Lee | Bitonic | WLS | NLLR | ADMSS | SRAD | SRAD-Guided | SAR-BM3D | Proposed | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Airplane | 0.21 | 0.29 | 0.28 | 0.37 | 0.50 | 0.66 | 0.70 | 0.25 | 0.73 | 0.72 | 0.76 | 0.84 | 0.82 |
| Baboon | 0.49 | 0.56 | 0.56 | 0.47 | 0.54 | 0.52 | 0.53 | 0.53 | 0.39 | 0.65 | 0.53 | 0.56 | 0.61 |
| Barbara | 0.44 | 0.61 | 0.57 | 0.50 | 0.60 | 0.64 | 0.67 | 0.55 | 0.52 | 0.68 | 0.65 | 0.84 | 0.69 |
| Boat | 0.33 | 0.46 | 0.44 | 0.47 | 0.60 | 0.68 | 0.67 | 0.40 | 0.39 | 0.71 | 0.70 | 0.72 | 0.73 |
| Camera-man | 0.42 | 0.49 | 0.48 | 0.48 | 0.57 | 0.67 | 0.73 | 0.45 | 0.36 | 0.76 | 0.74 | 0.80 | 0.80 |
| Fruits | 0.18 | 0.28 | 0.27 | 0.33 | 0.48 | 0.64 | 0.70 | 0.23 | 0.43 | 0.76 | 0.76 | 0.78 | 0.78 |
| Hill | 0.38 | 0.56 | 0.54 | 0.53 | 0.64 | 0.69 | 0.68 | 0.49 | 0.58 | 0.73 | 0.71 | 0.73 | 0.73 |
| House | 0.25 | 0.41 | 0.38 | 0.41 | 0.53 | 0.67 | 0.71 | 0.33 | 0.53 | 0.78 | 0.76 | 0.84 | 0.78 |
| Lena | 0.29 | 0.45 | 0.43 | 0.45 | 0.60 | 0.73 | 0.75 | 0.38 | 0.47 | 0.81 | 0.75 | 0.84 | 0.83 |
| Man | 0.37 | 0.56 | 0.54 | 0.54 | 0.66 | 0.72 | 0.71 | 0.50 | 0.50 | 0.76 | 0.74 | 0.76 | 0.77 |
| Monarch | 0.31 | 0.60 | 0.55 | 0.53 | 0.69 | 0.81 | 0.83 | 0.47 | 0.80 | 0.86 | 0.88 | 0.90 | 0.89 |
| Napoli | 0.49 | 0.72 | 0.69 | 0.61 | 0.69 | 0.70 | 0.68 | 0.67 | 0.66 | 0.77 | 0.70 | 0.73 | 0.75 |
| Peppers | 0.36 | 0.54 | 0.52 | 0.54 | 0.65 | 0.77 | 0.77 | 0.46 | 0.36 | 0.82 | 0.82 | 0.83 | 0.84 |
| Zelda | 0.35 | 0.61 | 0.58 | 0.55 | 0.70 | 0.80 | 0.82 | 0.51 | 0.77 | 0.86 | 0.85 | 0.87 | 0.86 |
| SRAD Filter | Soft Threshold | IGF | GF | Proposed | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | PSNR | SSIM | |
| Airplane | 26.97 | 0.72 | 26.94 (−0.03) | 0.73 (+0.01) | 26.98 (+0.01) | 0.72 (0.00) | 27.48 (+0.51) | 0.82 (+0.10) | 27.45 | 0.82 |
| Baboon | 23.52 | 0.65 | 22.69 (−0.83) | 0.60 (−0.05) | 23.53 (+0.01) | 0.65 (0.00) | 23.78 (+0.26) | 0.66 (+0.01) | 22.92 | 0.61 |
| Barbara | 24.99 | 0.68 | 24.32 (−0.67) | 0.66 (−0.02) | 25.00 (+0.01) | 0.68 (0.00) | 25.30 (+0.31) | 0.71 (+0.03) | 24.59 | 0.69 |
| Boat | 27.37 | 0.71 | 27.23 (−0.14) | 0.70 (−0.01) | 27.39 (+0.02) | 0.71 (0.00) | 27.67 (+0.30) | 0.73 (+0.02) | 27.55 | 0.73 |
| Cameraman | 26.73 | 0.76 | 26.69 (−0.04) | 0.76 (0.00) | 26.74 (+0.01) | 0.76 (0.00) | 26.90 (+0.17) | 0.80 (+0.04) | 26.87 | 0.80 |
| Fruits | 27.45 | 0.76 | 27.44 (−0.01) | 0.76 (0.00) | 27.46 (+0.01) | 0.78 (+0.02) | 27.45 (0.00) | 0.78 (+0.02) | 27.45 | 0.78 |
| Hill | 28.25 | 0.73 | 28.06 (−0.19) | 0.72 (−0.01) | 28.27 (+0.02) | 0.73 (0.00) | 28.41 (+0.16) | 0.74 (+0.01) | 28.27 | 0.73 |
| House | 27.58 | 0.78 | 27.92 (+0.34) | 0.70 (−0.08) | 27.98 (+0.40) | 0.70 (−0.08) | 28.64 (+1.06) | 0.78 (0.00) | 28.58 | 0.78 |
| Lena | 29.69 | 0.81 | 29.69 (0.00) | 0.81 (0.00) | 29.70 (+0.01) | 0.81 (0.00) | 29.72 (+0.03) | 0.82 (+0.01) | 30.13 | 0.83 |
| Man | 28.31 | 0.76 | 28.14 (−0.17) | 0.75 (−0.01) | 28.30 (−0.01) | 0.76 (0.00) | 28.52 (+0.21) | 0.77 (+0.01) | 28.55 | 0.77 |
| Monarch | 29.50 | 0.86 | 29.42 (−0.08) | 0.86 (0.00) | 29.51 (+0.01) | 0.86 (0.00) | 29.71 (+0.21) | 0.89 (+0.03) | 29.64 | 0.89 |
| Napoli | 26.41 | 0.77 | 25.72 (−0.69) | 0.75 (−0.02) | 26.41 (0.00) | 0.77 (0.00) | 26.39 (−0.02) | 0.78 (+0.01) | 25.70 | 0.75 |
| Peppers | 28.29 | 0.82 | 28.21 (−0.08) | 0.82 (0.00) | 28.31 (+0.02) | 0.82 (0.00) | 28.38 (+0.09) | 0.84 (+0.02) | 28.44 | 0.84 |
| Zelda | 32.67 | 0.86 | 32.67 (0.00) | 0.86 (0.00) | 32.68 (+0.01) | 0.86 (0.00) | 32.78 (+0.11) | 0.86 (0.00) | 32.77 | 0.86 |
| Avg. | −0.19 | −0.01 | +0.04 | 0.00 | +0.24 | +0.02 | ||||
| SRAD Filter | IGF | GF | |
|---|---|---|---|
| SAR image1 | Time step = 0.01 Exponential decay rate = 1 Number of iterations = 140 | Mask size = 33 × 33 Regularization parameter = 0.0001 | Mask size = 3 × 3 Regularization parameter = 0.001 |
| SAR image2 | Time step = 0.01 Exponential decay rate = 1 Number of iterations = 145 | Mask size = 33 × 33 Regularization parameter = 0.0001 | Mask size = 3 × 3 Regularization parameter = 0.001 |
| NLM | Guided | Frost | Lee | Bitonic | WLS | NLLR | ADMSS | SRAD | SRAD-Guided | SAR-BM3D | Proposed | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ROI1 (61 × 71) | 50.80 | 17.89 | 47.59 | 64.94 | 91.46 | 165.71 | 21.61 | 18.59 | 114.10 | 125.44 | 135.16 | 141.78 |
| ROI2 (51 × 71) | 40.87 | 16.25 | 37.85 | 49.15 | 64.98 | 118.11 | 19.41 | 16.78 | 81.01 | 88.88 | 85.09 | 99.92 |
| NLM | Guided | Frost | Lee | Bitonic | WLS | NLLR | ADMSS | SRAD | SRAD-Guided | SAR-BM3D | Proposed | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| ROI1 (61 × 71) | 29.53 | 16.17 | 48.47 | 62.14 | 99.30 | 207.56 | 21.20 | 201.56 | 146.91 | 174.02 | 186.54 | 205.89 |
| ROI2 (81 × 51) | 28.66 | 13.13 | 39.43 | 50.79 | 80.55 | 180.37 | 20.56 | 124.83 | 117.17 | 141.30 | 129.35 | 160.67 |
| SRAD Filter | Soft Threshold | IGF | GF | Proposed | ||||||
|---|---|---|---|---|---|---|---|---|---|---|
| ROI-1 | ROI-2 | ROI-1 | ROI-2 | ROI-1 | ROI-2 | ROI-1 | ROI-2 | ROI-1 | ROI-2 | |
| SAR image1 | 114.10 | 81.01 | 114.62 (+0.52) | 81.59 (+0.58) | 118.84 (+4.74) | 84.09 (+2.29) | 136.52 (+22.42) | 97.05 (+16.04) | 141.78 | 99.92 |
| SAR image2 | 146.91 | 117.17 | 147.76 (+0.85) | 118.50 (+1.33) | 148.93 (+2.02) | 119.27 (+2.10) | 203.02 (+56.11) | 157.24 (+40.07) | 205.89 | 160.67 |
| Avg. | +0.69 | +0.96 | +3.38 | +2.20 | +39.27 | +68.56 | ||||
| NLM | Guided | Frost | Lee | Bitonic | WLS | NLLR | ADMSS | SRAD | SRAD-Guided | SAR-BM3D | Proposed | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| Airplane | 0.48 | 0.16 | 1.86 | 6.41 | 0.09 | 3.51 | 1052.12 | 196.87 | 5.51 | 5.92 | 61.50 | 5.70 |
| Baboon | 0.48 | 0.11 | 2.00 | 7.29 | 0.10 | 0.48 | 1030.23 | 173.14 | 2.45 | 2.61 | 59.84 | 2.76 |
| Barbara | 0.50 | 0.12 | 2.05 | 7.28 | 0.08 | 1.00 | 1003.88 | 162.76 | 3.44 | 3.74 | 59.36 | 3.74 |
| Boat | 0.48 | 0.11 | 2.01 | 7.28 | 0.09 | 0.98 | 1007.25 | 174.22 | 5.06 | 5.48 | 61.07 | 5.36 |
| Cameraman | 0.12 | 0.08 | 0.52 | 1.88 | 0.03 | 0.46 | 211.28 | 21.64 | 1.55 | 1.21 | 14.45 | 1.91 |
| Fruits | 0.48 | 0.11 | 2.03 | 7.31 | 0.09 | 0.97 | 1012.13 | 181.41 | 7.40 | 7.85 | 62.17 | 7.84 |
| Hill | 0.48 | 0.11 | 1.98 | 7.25 | 0.09 | 0.99 | 1061.75 | 162.39 | 4.98 | 5.62 | 61.38 | 5.28 |
| House | 0.12 | 0.09 | 0.53 | 1.92 | 0.03 | 0.49 | 231.46 | 28.01 | 1.54 | 1.05 | 14.34 | 1.83 |
| Lena | 0.48 | 0.16 | 1.86 | 6.47 | 0.10 | 1.00 | 1081.19 | 170.44 | 7.53 | 8.03 | 60.16 | 7.71 |
| Man | 0.48 | 0.11 | 1.99 | 7.32 | 0.09 | 1.09 | 1057.03 | 165.61 | 5.23 | 5.70 | 60.15 | 5.40 |
| Monarch | 0.73 | 0.13 | 2.85 | 9.77 | 0.12 | 1.51 | 1661.38 | 277.26 | 8.48 | 5.96 | 87.94 | 8.93 |
| Napoli | 0.50 | 0.12 | 1.90 | 6.64 | 0.08 | 1.07 | 1060.22 | 168.11 | 4.02 | 4.10 | 59.55 | 4.31 |
| Peppers | 0.12 | 0.09 | 0.50 | 1.71 | 0.03 | 0.50 | 218.14 | 26.96 | 1.04 | 1.16 | 14.49 | 1.32 |
| Zelda | 0.48 | 0.12 | 1.88 | 6.88 | 0.09 | 0.99 | 1001.87 | 164.50 | 7.10 | 7.45 | 59.57 | 7.32 |
| Avg. | 0.42 | 0.12 | 1.71 | 6.10 | 0.08 | 1.07 | 906.42 | 148.09 | 4.67 | 4.71 | 52.57 | 5.06 |
| NLM | Guided | Frost | Lee | Bitonic | WLS | NLLR | ADMSS | SRAD | SRAD-Guided | SAR-BM3D | Proposed | |
|---|---|---|---|---|---|---|---|---|---|---|---|---|
| SAR image1 | 0.16 | 0.08 | 0.46 | 0.45 | 0.10 | 0.17 | 222.16 | 29.41 | 1.14 | 1.08 | 14.40 | 1.56 |
| SAR image2 | 0.47 | 0.19 | 1.73 | 6.23 | 0.12 | 0.71 | 1071.83 | 191.19 | 7.09 | 7.48 | 62.95 | 7.45 |
| Avg. | 0.32 | 0.14 | 1.10 | 3.34 | 0.11 | 0.44 | 647.04 | 110.30 | 4.12 | 4.28 | 38.68 | 4.50 |
| Image Size | Time for SRAD | Time for Soft Threshold | Time for IGF | Time for GF | Total Time | |
|---|---|---|---|---|---|---|
| Airplane | 512 × 512 | 5.51 | 0.11 | 0.05 | 0.03 | 5.70 |
| Baboon | 512 × 512 | 2.45 | 0.11 | 0.17 | 0.03 | 2.76 |
| Barbara | 512 × 512 | 3.44 | 0.11 | 0.16 | 0.03 | 3.74 |
| Boat | 512 × 512 | 5.06 | 0.11 | 0.16 | 0.03 | 5.36 |
| Cameraman | 256 × 256 | 1.55 | 0.10 | 0.23 | 0.03 | 1.91 |
| Fruits | 512 × 512 | 7.40 | 0.11 | 0.30 | 0.03 | 7.84 |
| Hill | 512 × 512 | 4.98 | 0.11 | 0.16 | 0.03 | 5.28 |
| House | 512 × 512 | 1.54 | 0.10 | 0.16 | 0.03 | 1.83 |
| Lena | 512 × 512 | 7.53 | 0.11 | 0.04 | 0.03 | 7.71 |
| Man | 512 × 512 | 5.23 | 0.12 | 0.05 | 0.03 | 5.40 |
| Monarch | 748 × 512 | 8.48 | 0.12 | 0.30 | 0.03 | 8.93 |
| Napoli | 512 × 512 | 4.02 | 0.12 | 0.13 | 0.04 | 4.31 |
| Peppers | 256 × 256 | 1.04 | 0.11 | 0.14 | 0.03 | 1.32 |
| Zelda | 512 × 512 | 7.10 | 0.12 | 0.10 | 0.03 | 7.32 |
| Avg. | 4.67 | 0.11 | 0.15 | 0.03 | 4.96 |
| Image Size | Time for SRAD | Time for Soft Threshold | Time for IGF | Time for GF | Total Time | |
|---|---|---|---|---|---|---|
| SAR Image1 | 256 × 256 | 1.14 | 0.10 | 0.29 | 0.03 | 1.56 |
| SAR Image2 | 512 × 512 | 7.09 | 0.11 | 0.22 | 0.03 | 7.45 |
| Avg. | 4.12 | 0.10 | 0.26 | 0.03 | 4.50 |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Choi, H.; Jeong, J. Speckle Noise Reduction Technique for SAR Images Using Statistical Characteristics of Speckle Noise and Discrete Wavelet Transform. Remote Sens. 2019, 11, 1184. https://doi.org/10.3390/rs11101184
Choi H, Jeong J. Speckle Noise Reduction Technique for SAR Images Using Statistical Characteristics of Speckle Noise and Discrete Wavelet Transform. Remote Sensing. 2019; 11(10):1184. https://doi.org/10.3390/rs11101184
Chicago/Turabian StyleChoi, Hyunho, and Jechang Jeong. 2019. "Speckle Noise Reduction Technique for SAR Images Using Statistical Characteristics of Speckle Noise and Discrete Wavelet Transform" Remote Sensing 11, no. 10: 1184. https://doi.org/10.3390/rs11101184
APA StyleChoi, H., & Jeong, J. (2019). Speckle Noise Reduction Technique for SAR Images Using Statistical Characteristics of Speckle Noise and Discrete Wavelet Transform. Remote Sensing, 11(10), 1184. https://doi.org/10.3390/rs11101184