Uncertainty Characterization and Propagation in the Community Long-Term Infrared Microwave Combined Atmospheric Product System (CLIMCAPS)
Abstract
:1. Introduction
2. Instruments and Inversion Methods
2.1. Hyperspectral Infrared Sounders
2.2. CLIMCAPS Infrared Inversion System
2.2.1. Bayesian Optimal-Estimation
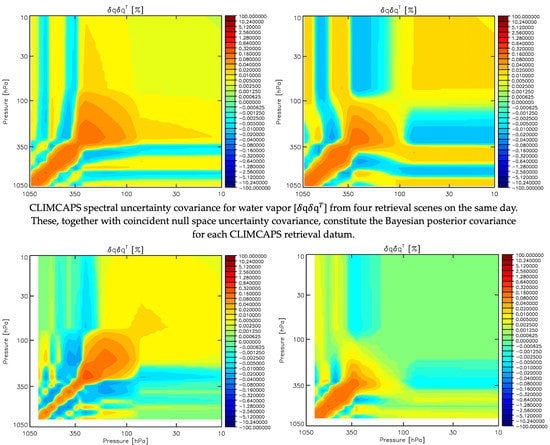
2.2.2. Scene-Dependent Uncertainty Propagation
2.2.3. Prior Estimate of Atmospheric State
2.2.4. Cloud Clearing
3. Results and Discussion
3.1. Datum-Specific Uncertainty Metrics
3.2. Retrieved Essential Climate Variables—Temperature and Water Vapor
4. Conclusions
Author Contributions
Funding
Acknowledgments
Conflicts of Interest
References
- Bowman, K.W.; Rodgers, C.D.; Kulawik, S.S.; Worden, J.; Sarkissian, E.; Osterman, G.; Steck, T.; Ming, L.; Eldering, A.; Shephard, M.; et al. Tropospheric emission spectrometer: Retrieval method and error analysis. IEEE Trans. Geosci. Remote Sens. 2006, 44, 1297–1307. [Google Scholar] [CrossRef]
- Susskind, J.; Barnet, C.D.; Blaisdell, J.M. Retrieval of atmospheric and surface parameters from AIRS/AMSU/HSB data in the presence of clouds. IEEE Trans. Geosci. Remote Sens. 2003, 41, 390–409. [Google Scholar] [CrossRef]
- Deeter, M.N. Operational carbon monoxide retrieval algorithm and selected results for the MOPITT instrument. J. Geophys. Res. 2003, 108. [Google Scholar] [CrossRef]
- Deeter, M.N.; Edwards, D.P.; Gille, J.C.; Emmons, L.K.; Francis, G.; Ho, S.-P.; Mao, D.; Masters, D.; Worden, H.; Drummond, J.R.; et al. The MOPITT version 4 CO product: Algorithm enhancements, validation, and long-term stability. J. Geophys. Res. 2010, 115. [Google Scholar] [CrossRef] [Green Version]
- Rodgers, C.D. Retrieval of atmospheric temperature and composition from remote measurements of thermal radiation. Rev. Geophys. 1976, 14, 609–624. [Google Scholar] [CrossRef]
- Rodgers, C.D. Characterization and error analysis of profiles retrieved from remote sounding measurements. J. Geophys. Res. 1990, 95, 5587–5595. [Google Scholar] [CrossRef]
- Rodgers, C.D. Information content and optimisation of high spectral resolution remote measurements. Adv. Space Res. 1998, 21, 361–367. [Google Scholar] [CrossRef]
- Rodgers, C.D. Inverse Methods for Atmospheric Sounding: Theory and Practice; World Scientific: Singapore; Hackensack, NJ, USA, 2000; ISBN 978-981-02-2740-1. [Google Scholar]
- GCOS. Systematic Observation Requirements for Satellite-BASED products for Climate; WMO GCOS: Geneva, Switzerland, 2011; p. 127. [Google Scholar]
- Smith, N.; Smith, W.L.; Weisz, E.; Revercomb, H.E. AIRS, IASI and CrIS retrieval records at climate scales: An investigation into the propagation systematic uncertainty. J. Appl. Meteorol. Climatol. 2015, 54, 1465–1481. [Google Scholar] [CrossRef]
- Gaudel, A.; Cooper, O.R.; Ancellet, G.; Barret, B.; Boynard, A.; Burrows, J.P.; Clerbaux, C.; Coheur, P.-F.; Cuesta, J.; Cuevas, E.; et al. Tropospheric Ozone Assessment Report: Present-day distribution and trends of tropospheric ozone relevant to climate and global atmospheric chemistry model evaluation. Elem. Sci. Anth. 2018, 6, 39. [Google Scholar] [CrossRef]
- Shephard, M.W.; Cady-Pereira, K.E. Cross-track Infrared Sounder (CrIS) satellite observations of tropospheric ammonia. Atmos. Meas. Tech. 2015, 8, 1323–1336. [Google Scholar] [CrossRef] [Green Version]
- Gambacorta, A.; Barnet, C.D. Methodology and Information Content of the NOAA NESDIS Operational Channel Selection for the Cross-Track Infrared Sounder (CrIS). IEEE Trans. Geosci. Remote Sens. 2013, 51, 3207–3216. [Google Scholar] [CrossRef]
- Chahine, M.T.; Pagano, T.S.; Aumann, H.H.; Atlas, R.; Barnet, C.; Blaisdell, J.; Chen, L.; Divakarla, M.; Fetzer, E.J.; Goldberg, M.; et al. AIRS: Improving Weather Forecasting and Providing New Data on Greenhouse Gases. Bull. Am. Meteorol. Soc. 2006, 87, 911–926. [Google Scholar] [CrossRef]
- Weisz, E.; Smith, N.; Smith, W.L.; Strabala, K.; Huang, H.L. Assessing Hyperspectral Retrieval Algorithms and Their Products for Use in Direct Broadcast Applications. In Proceedings of the 20th International TOVS Study Conference (ITSC-20) Proceedings, Lake Geneva, WI, USA, 28 October–3 November 2015. [Google Scholar]
- Weisz, E.; Smith, N.; Smith, W.L. The use of hyperspectra sounding information to monitor atmospheric tendencies leading to severe local storms. Earth Space Sci. 2015, 2, 369–377. [Google Scholar] [CrossRef]
- Berndt, E.; Folmer, M. Utility of CrIS/ATMS profiles to diagnose extratropical transition. Results Phys. 2018, 8, 184–185. [Google Scholar] [CrossRef]
- Berndt, E.B.; Zavodsky, B.T.; Folmer, M.J. Development and Application of Atmospheric Infrared Sounder Ozone Retrieval Products for Operational Meteorology. IEEE Trans. Geosci. Remote Sens. 2016, 54, 958–967. [Google Scholar] [CrossRef]
- Smith, W.L. Atmospheric soundings from satellites—False expectation or the key to improved weather prediction? Q. J. R. Meteorol. Soc. 1991, 117, 267–297. [Google Scholar]
- Iturbide-Sanchez, F.; da Silva, S.R.S.; Liu, Q.; Pryor, K.L.; Pettey, M.E.; Nalli, N.R. Toward the Operational Weather Forecasting Application of Atmospheric Stability Products Derived from NUCAPS CrIS/ATMS Soundings. IEEE Trans. Geosci. Remote Sens. 2018, 56, 4522–4545. [Google Scholar] [CrossRef]
- Smith, N.; White, K.D.; Berndt, E.B.; Zavodsky, B.T.; Wheeler, A.; Bowlan, M.A.; Barnet, C.D. NUCAPS in AWIPS–Rethinking information compression and distribution for fast decision making. In Proceedings of the 98th America Meteorological Society Annual Meeting, Austin, TX, USA, 7–11 January 2018. [Google Scholar]
- Smith, N.; Berndt, E.B.; Barnet, C.D.; Goldberg, M.D. Why operational meteorologists need more satellite soundings. In Proceedings of the 99th America Meteorological Society Annual Meeting, Phoenix, AZ, USA, 6–10 January 2019. [Google Scholar]
- Ackerman, S.A.; Platnick, S.; Bhartia, P.K.; Duncan, B.; L’Ecuyer, T.; Heidinger, A.; Skofronick-Jackson, G.; Loeb, N.; Schmit, T.; Smith, N. Satellites See the World’s Atmosphere. Meteorol. Monogr. 2018, 59, 4.1–4.53. [Google Scholar] [CrossRef]
- Rodgers, C.D. Remote sensing of the atmospheric temperature profile in the presence of cloud. Q. J. R. Meteorol. Soc. 1970, 96, 654–666. [Google Scholar] [CrossRef]
- Eyre, J.R. The information content of data from satellite sounding systems: A simulation study. Q. J. R. Meteorol. Soc. 1990, 116, 401–434. [Google Scholar] [CrossRef]
- Eyre, J.R. Inversion of cloudy satellite sounding radiances by nonlinear optimal estimation. I: Theory and simulation for TOVS. Q. J. R. Meteorol. Soc. 1989, 115, 1001–1026. [Google Scholar] [CrossRef]
- Eyre, J.R. Inversion of cloudy satellite sounding radiances by nonlinear optimal estimation. II: Application to TOVS data. Q. J. R. Meteorol. Soc. 1989, 115, 1027–1037. [Google Scholar] [CrossRef]
- Susskind, J.; Blaisdell, J.M.; Iredell, L. Improved methodology for surface and atmospheric soundings, error estimates, and quality control procedures: The atmospheric infrared sounder science team version-6 retrieval algorithm. J. Appl. Remote Sens. 2014, 8, 084994. [Google Scholar] [CrossRef]
- Susskind, J.; Blaisdell, J.M.; Iredell, L.; Keita, F. Improved Temperature Sounding and Quality Control Methodology Using AIRS/AMSU Data: The AIRS Science Team Version 5 Retrieval Algorithm. IEEE Trans. Geosci. Remote Sens. 2011, 49, 883–907. [Google Scholar] [CrossRef]
- Goldberg, M.D.; Kilcoyne, H.; Cikanek, H.; Mehta, A. Joint Polar Satellite System: The United States next generation civilian polar-orbiting environmental satellite system: USA NEXT GENERATION SATELLITE SYSTEM. J. Geophys. Res. Atmos. 2013, 118, 13463–13475. [Google Scholar] [CrossRef]
- Sun, B.; Reale, A.; Tilley, F.H.; Pettey, M.E.; Nalli, N.R.; Barnet, C.D. Assessment of NUCAPS S-NPP CrIS/ATMS Sounding Products Using Reference and Conventional Radiosonde Observations. IEEE J. Sel. Top. Appl. Earth Obs. Remote Sens. 2017, 10, 2499–2509. [Google Scholar] [CrossRef]
- Nalli, N.R.; Gambacorta, A.; Liu, Q.; Barnet, C.D.; Tan, C.; Iturbide-Sanchez, F.; Reale, T.; Sun, B.; Wilson, M.; Borg, L.; et al. Validation of Atmospheric Profile Retrievals from the SNPP NOAA-Unique Combined Atmospheric Processing System. Part 1: Temperature and Moisture. IEEE Trans. Geosci. Remote Sens. 2018, 56, 180–190. [Google Scholar] [CrossRef]
- Nalli, N.R.; Gambacorta, A.; Liu, Q.; Tan, C.; Iturbide-Sanchez, F.; Barnet, C.D.; Joseph, E.; Morris, V.R.; Oyola, M.; Smith, J.W. Validation of Atmospheric Profile Retrievals from the SNPP NOAA-Unique Combined Atmospheric Processing System. Part 2: Ozone. IEEE Trans. Geosci. Remote Sens. 2018, 56, 598–607. [Google Scholar] [CrossRef]
- Trenberth, K.E.; Anthes, R.A.; Belward, A.; Brown, O.B.; Habermann, T.; Karl, T.R.; Running, S.; Ryan, B.; Tanner, M.; Wielicki, B. Challenges of a Sustained Climate Observing System. In Climate Science for Serving Society; Asrar, G.R., Hurrell, J.W., Eds.; Springer: Dordrecht, The Netherlands, 2013; pp. 13–50. ISBN 978-94-007-6691-4. [Google Scholar] [Green Version]
- Merchant, C.J.; Paul, F.; Popp, T.; Ablain, M.; Bontemps, S.; Defourny, P.; Hollmann, R.; Lavergne, T.; Laeng, A.; de Leeuw, G.; et al. Uncertainty information in climate data records from Earth observation. Earth Syst. Sci. Data 2017, 9, 511–527. [Google Scholar] [CrossRef] [Green Version]
- Mittaz, J.; Merchant, C.J.; Woolliams, E.R. Applying principles of metrology to historical Earth observations from satellites. Metrologia 2019. [Google Scholar] [CrossRef]
- Wylie, D.; Jackson, D.L.; Menzel, W.P.; Bates, J.J. Trends in Global Cloud Cover in Two Decades of HIRS Observations. J. Clim. 2005, 18, 3021–3031. [Google Scholar] [CrossRef]
- Pierrehumbert, R.T.; Hafemeister, D.; Kammen, D.; Levi, B.G.; Schwartz, P. Infrared Radiation and Planetary Temperature. AIP Conf. Proc. 2011, 1401, 232–244. [Google Scholar]
- Smith, W.L.; Revercomb, H.E.; Bingham, G.; Larar, A.; Huang, H.L.; Zhou, D.K.; Li, J.; Liu, X.; Kireev, S.V. Technical note: Evolution, current capabilities, and future advance in satellite nadir viewing ultra-spectral IR sounding of the lower atmopshere. Atmos. Chem. Phys. 2009, 9, 5563–5574. [Google Scholar] [CrossRef]
- Le Marshall, J.; Jung, J.; Derber, J.; Chahine, M.; Treadon, R.; Lord, S.J.; Goldberg, M.; Wolf, W.; Liu, H.C.; Joiner, J.; et al. Improving Global Analysis and Forecasting with AIRS. Bull. Am. Meteorol. Soc. 2006, 87, 891–895. [Google Scholar] [CrossRef] [Green Version]
- Jones, T.A.; Stensrud, D.J. Assimilating AIRS Temperature and Mixing Ratio Profiles Using an Ensemble Kalman Filter Approach for Convective-Scale Forecasts. Weather Forecast. 2012, 27, 541–564. [Google Scholar] [CrossRef]
- Collard, A.D.; Healy, S.B. The combined impact of future space-based atmospheric sounding instruments on numerical weather-prediction analysis fields: A simulation study. Q. J. R. Meteorol. Soc. 2003, 129, 2741–2760. [Google Scholar] [CrossRef]
- Gettelman, A.; Fu, Q. Observed and Simulated Upper-Tropospheric Water Vapor Feedback. J. Clim. 2008, 21, 3282–3289. [Google Scholar] [CrossRef] [Green Version]
- Fasullo, J.T.; Trenberth, K.E. A Less Cloudy Future: The Role of Subtropical Subsidence in Climate Sensitivity. Science 2012, 338, 792–794. [Google Scholar] [CrossRef] [PubMed]
- Dessler, A.E.; Zhang, Z.; Yang, P. Water-vapor climate feedback inferred from climate fluctuations, 2003–2008. Geophys. Res. Lett. 2008, 35. [Google Scholar] [CrossRef]
- Smith, W.L.; Weisz, E.; Kireev, S.V.; Zhou, D.K.; Li, Z.; Borbas, E.E. Dual-regression retrieval algorithm for real-time processing of satellite ultraspectral radiances. J. Appl. Meteorol. Climatol. 2012, 51, 1455–1476. [Google Scholar] [CrossRef]
- Weisz, E.; Smith, W.L.; Smith, N. Advances in simultaneous atmospheric profile and cloud parameter regression based retrieval from high-spectral resolution radiance measurements. J. Geophys. Res. Atmos. 2013, 118, 6433–6443. [Google Scholar] [CrossRef]
- Aumann, H.H.; Chahine, M.T.; Gautier, C.; Goldberg, M.D.; Kalnay, E.; McMillin, L.M.; Revercomb, H.; Rosenkranz, P.W.; Smith, W.L.; Staelin, D.H.; et al. AIRS/AMSU/HSB on the aqua mission: Design, science objectives, data products, and processing systems. IEEE Trans. Geosci. Remote Sens. 2003, 41, 253–264. [Google Scholar] [CrossRef]
- Pagano, T.S.; Aumann, H.H.; Manning, E.M.; Elliott, D.A.; Broberg, S.E. Improving AIRS Radiance Spectra in High Contrast Scenes Using MODIS. In Proceedings of the SPIE 9607, Earth Observing Systems XX, San Diego, CA, USA, 8 September 2015; p. 96070K. [Google Scholar]
- Glumb, R.J.; Jordan, D.C.; Mantica, P. Development of the Crosstrack Infrared Sounder (CrIS) Sensor Design. In Proceedings of the SPIE 4486, Infrared Spaceborne Remote Sensing IX, San Diego, CA, USA, 8 February 2002; pp. 411–424. [Google Scholar]
- Merchant, C.; Holl, G.; Mittaz, J.; Woolliams, E. Radiance Uncertainty Characterisation to Facilitate Climate Data Record Creation. Remote Sens. 2019, 11, 474. [Google Scholar] [CrossRef]
- Blackwell, W.J. Neural network Jacobian analysis for high-resolution profiling of the atmosphere. EURASIP J. Adv. Signal Process. 2012, 2012, 71. [Google Scholar] [CrossRef] [Green Version]
- Blackwell, W.J. Validation of Neural Network Atmospheric Temperature and Moisture Retrievals Using AIRS/AMSU Radiances. In Proceedings of the SPIE 5806, Algorithms and Technologies for Multispectral, Hyperspectral, and Ultraspectral Imagery XI, Orlando, FL, USA, 1 June 2005. [Google Scholar]
- Blackwell, W.J. A neural-network technique for the retrieval of atmospheric temperature and moisture profiles from high spectral resolution sounding data. IEEE Trans. Geosci. Remote Sens. 2005, 43, 2535–2546. [Google Scholar] [CrossRef]
- Blackwell, W.J.; Chen, F.W. Neural Networks in Atmospheric Remote Sensing; Artech House: Boston, MA, USA, 2009; ISBN 978-1-59693-372-9. [Google Scholar]
- Motteler, H.E.; Strow, L.L.; McMillin, L.; Gualtieri, J.A. Comparison of neural networks and regression-based methods for temperature retrievals. Appl. Opt. 1995, 34, 5390. [Google Scholar] [CrossRef] [PubMed]
- Goldberg, D.G.; Qu, Y.; McMillim, L.M.; Wolf, W.; Zhou, L.; Divakarla, G. AIRS near-real-time products and algorithms in support of operational numerical weather prediction. IEEE Trans. Geosci. Remote Sens. 2003, 41, 379–389. [Google Scholar] [CrossRef]
- Smith, W.L.; Weisz, E. Dual-regression approach for high-spatial-resolution infrared soundings. Compr. Remote Sens. 2018, 7, 297–311. [Google Scholar]
- Weisz, E.; Huang, H.L.; Li, J.; Borbas, E.E.; Baggett, K.; Thapliyal, P.; Guan, L. International MODIS and AIRS processing package: AIRS products and applications. J. Appl. Remote Sens. 2007, 1, 013519. [Google Scholar] [CrossRef]
- Molod, A.; Takacs, L.; Suarez, M.; Bacmeister, J. Development of the GEOS-5 atmospheric general circulation model: Evolution from MERRA to MERRA2. Geosci. Model Dev. 2015, 8, 1339–1356. [Google Scholar] [CrossRef]
- Gelaro, R.; McCarty, W.; Suárez, M.J.; Todling, R.; Molod, A.; Takacs, L.; Randles, C.A.; Darmenov, A.; Bosilovich, M.G.; Reichle, R.; et al. The Modern-Era Retrospective Analysis for Research and Applications, Version 2 (MERRA-2). J. Clim. 2017, 30, 5419–5454. [Google Scholar] [CrossRef]
- Rabier, F.; Thépaut, J.-N.; Courtier, P. Extended assimilation and forecast experiments with a four-dimensional variational assimilation system. Q. J. R. Meteorol. Soc. 1998, 124, 1861–1887. [Google Scholar] [CrossRef]
- Rabier, F.; Järvinen, H.; Klinker, E.; Mahfouf, J.-F.; Simmons, A. The ECMWF operational implementation of four-dimensional variational assimilation. I: Experimental results with simplified physics. Q. J. R. Meteorol. Soc. 2007, 126, 1143–1170. [Google Scholar] [CrossRef]
- Li, J.; Menzel, W.P.; Sun, F.; Schmit, T.J.; Gurka, J.J. AIRS subpixel cloud characterization using MODIS cloud products. J. Appl. Meteorol. 2004, 43, 1083–1094. [Google Scholar] [CrossRef]
- Li, J.; Liu, C.Y.; Huang, H.L.; Schmit, T.J.; Wu, X.; Menzel, W.P.; Gurka, J.J. Optimal cloud-clearing for AIRS radiances using MODIS. IEEE Trans. Geosci. Remote Sens. 2005, 43, 1266–1278. [Google Scholar]
- Maddy, E.S.; King, T.S.; Sun, H.; Wolf, W.W.; Barnet, C.D.; Heidinger, A.; Cheng, Z.; Goldberg, M.D.; Gambacorta, A.; Zhang, C.; et al. Using MetOp-A AVHRR Clear-Sky Measurements to Cloud-Clear MetOp-A IASI Column Radiances. J. Atmos. Ocean. Technol. 2011, 28, 1104–1116. [Google Scholar] [CrossRef]
- Mayer, B. Radiative transfer in the cloudy atmosphere. Eur. Phys. J. Conf. 2009, 1, 75–99. [Google Scholar] [CrossRef]
- Irion, F.W.; Kahn, B.H.; Schreier, M.M.; Fetzer, E.J.; Fishbein, E.; Fu, D.; Kalmus, P.; Wilson, R.C.; Wong, S.; Yue, Q. Single-footprint retrievals of temperature, water vapor and cloud properties from AIRS. Atmos. Meas. Tech. 2018, 11, 971–995. [Google Scholar] [CrossRef] [Green Version]
- DeSouza-Machado, S.; Strow, L.L.; Tangborn, A.; Huang, X.; Chen, X.; Liu, X.; Wu, W.; Yang, Q. Single-footprint retrievals for AIRS using a fast TwoSlab cloud-representation model and the SARTA all-sky infrared radiative transfer algorithm. Atmos. Meas. Tech. 2018, 11, 529–550. [Google Scholar] [CrossRef] [Green Version]
- Smith, W.L. An improved method for calculating tropospheric temperature and moisture from satellite radiometer measurements. Mon. Weather Rev. 1968, 96, 387–396. [Google Scholar] [CrossRef]
- Chahine, M.T. Remote sounding of cloudy atmospheres. I. The single cloud layer. J. Atmos. Sci. 1974, 31, 233–243. [Google Scholar] [CrossRef]
- Chahine, M.T. Inverse Problems in Radiative Transfer: Determination of Atmospheric Parameters. J. Atmos. Sci. 1970, 27, 960–967. [Google Scholar] [CrossRef]
- Maddy, E.S.; Barnet, C.D. Vertical Resolution Estimates in Version 5 of AIRS Operational Retrievals. IEEE Trans. Geosci. Remote Sens. 2008, 46, 2375–2384. [Google Scholar] [CrossRef]












| Instrument Type | AIRS 1 Grating | IASI 2 Interferometer | CrIS 3 Interferometer |
|---|---|---|---|
| Satellite | Aqua | MetOp-A, MetOp-B | SNPP, NOAA-20 |
| Launch | 2002/05/04 | 2006/10/19, 2012/09/17 | 2011/10/28, 2017/11/18 |
| Local Overpass Time | 13:30 | 21:30 | 13:30 |
| Altitude (km) | 705 | 833 | 824 |
| Mass (kg) | 177 | 236 | 147 |
| Period (min) | 98.8841 | 101.3592 | 101.4978 |
| Orbits/day | 14.5625 | 14.2070 | 14.1875 |
| FOV (deg) | 1.1100 | 0.840 | 0.963 |
| FOV (km) | 13.5 | 12 | 14 |
| # FOV per FOR 50km@nadir | 9 | 4 | 9 |
| # FOR 4 per day | 30 × 10,800 = 324,000 | 30 × 10,800 = 324,000 | 30 × 10,800 = 324,000 |
| Total # IR spectral channels | 2378 | 8461 | NSR: 1305, FSR: 2211 |
| LW 5 band (645–1210 cm−1) | 1262 | 2260 | NSR: 713, FSR: 713 |
| MW 6 band (1210–2000 cm−1) | 602 | 3160 | NSR: 433, FSR: 863 |
| SW 7 band (2000–2760 cm−1) | 514 | 3041 | NSR: 159, FSR: 865 |
| Spectral sampling (cm−1) | v/2400, 0.25 to 1.07 | 0.25 (0.5/OPD) | NSR: 0.625, 1.25, 2.5 FSR: 0.625 (all bands) |
| Apodization Type | n/a | Gaussian (1.0/OPD) | Hamming (0.9/OPD) |
| Apodized Resolution (cm−1) | v/1200, 0.5 to 2.3 | 0.5 (all bands) | NSR: 1.125, 2.25, 4.5 FSR: 0.75 (all bands) |
| Noise characteristic | |||
| NEDT (T = 250 K) @ 700 cm−1 | 0.23 | 0.20 | NSR, FSR: 0.05 |
| NEDT (T = 250 K) @ 1400 cm−1 | 0.08 | 0.10 | NSR: 0.05, FSR: 0.07 |
| NEDT (T = 250 K) @ 2400 cm−1 | 0.14 | 1.9 | NSR: 0.2, FSR: 0.5 |
| Statistical Regression | MERRA2 Reanalysis |
|---|---|
Instrument Dependent: regression coefficients are calculated individually for each instrument and associated satellite configuration
| Instrument Independent: measurements from a multitude of instruments are assimilated in each analysis window
|
Scene Dependent: retrieves state variables one footprint at a time at the same spatial resolution as CLIMCAPS product
| Scene Independent: models atmospheric spatial gradients based on conservation of energy and momentum
|
| Temporally Static: regression coefficients are derived from a fixed set of focus days and thus do not capture decadal variation in atmospheric processes | Temporally Dynamic: assimilates the full long-term record of modern-era satellite instrument measurements to accurately represent change in climate variables such as CO2 |
| IR Spectral Dependence: uses all IR spectral channels from each instrument in retrieval. Highly dependent on full information content of AIRS and CrIS | IR Spectral Dependence: uses small subset of channels sensitive to temperature and water vapor. Low dependence on fraction of the spectral information content of AIRS and CrIS |
© 2019 by the authors. Licensee MDPI, Basel, Switzerland. This article is an open access article distributed under the terms and conditions of the Creative Commons Attribution (CC BY) license (http://creativecommons.org/licenses/by/4.0/).
Share and Cite
Smith, N.; Barnet, C.D. Uncertainty Characterization and Propagation in the Community Long-Term Infrared Microwave Combined Atmospheric Product System (CLIMCAPS). Remote Sens. 2019, 11, 1227. https://doi.org/10.3390/rs11101227
Smith N, Barnet CD. Uncertainty Characterization and Propagation in the Community Long-Term Infrared Microwave Combined Atmospheric Product System (CLIMCAPS). Remote Sensing. 2019; 11(10):1227. https://doi.org/10.3390/rs11101227
Chicago/Turabian StyleSmith, Nadia, and Christopher D. Barnet. 2019. "Uncertainty Characterization and Propagation in the Community Long-Term Infrared Microwave Combined Atmospheric Product System (CLIMCAPS)" Remote Sensing 11, no. 10: 1227. https://doi.org/10.3390/rs11101227
APA StyleSmith, N., & Barnet, C. D. (2019). Uncertainty Characterization and Propagation in the Community Long-Term Infrared Microwave Combined Atmospheric Product System (CLIMCAPS). Remote Sensing, 11(10), 1227. https://doi.org/10.3390/rs11101227